This is the second part of the article originally published in 2013 by the University of Notre Dame, and is republished here with permission. The first part was published in the January 2019 issue of Bhāvanā, and the third part will be published in a subsequent issue.
One of the most appealing presentations of basic elements of number theory appears in Plato’s dialogue Theaetetus, another in Book VII of Euclid. Both deal, the first only incidentally, with primes; the first also deals with the notion of irrational number, although in the guise of incommensurability.1 These two notions, of prime number and irrational number, are linked to this day and lie at the foundation of number theory. Both are familiar to many laymen; both can be readily explained to an attentive, reasonably intelligent auditor.
The modern theory of numbers is very abstruse. Even among its practitioners and in spite of the occasionally elementary nature of its conclusions, it is fragmented. Because of the often fortuitous composition of the faculty of the more popular graduate schools, some extremely technical aspects are familiar to many people, others known to almost none. This is inevitable. One can already see in the Xth book of Euclid how quickly the examination of the simplest irrationalities leads to what appear to be uselessly arcane reflections.
These reflections are closely related to the considerations of the modern Galois theory created by the very young mathematician Évariste Galois early in the nineteenth century.2 This theory, which analyses in a brief and incisive way, with the aid of the notion of a group of symmetries, the essential nature of algebraic irrationalities, is a part of the current undergraduate curriculum and modern pure mathematics would be unthinkable without it or without the notion of a group, which, as we shall see, penetrates mathematics far more broadly, far more deeply than Galois theory itself.

It is useful, as an introduction to Galois theory and to symmetries, but also to acquire some insight into the genesis of mathematical theories, to recall briefly the lengthy, but little read, Book X of Euclid’s Elements. It begins by a careful analysis of incommensurability and thus of the irrational, a word that it is best to use here in its modern mathematical sense and not in that of Euclid, or rather that of the English translation. Rational numbers are common fractions. Irrational numbers are the remaining numbers. Euclid and Galois are concerned by and large with irrational numbers that are also algebraic, thus they satisfy an algebraic equation of the form (1.1) in which all the coeffcients a_{n-1}, …, a_{0} are ordinary fractions, thus rational numbers.1 We have already emphasized that it is central to all of algebra and to a good deal of geometry that, whether or not the coeffcients are rational, the left-hand side of this equation may be written in exactly one way as
\[\begin{align}
X^n +a_{n-1}1X^{n-1}+a_{n-2}X^{n-2}+\cdots+ a_1 X+ a_0\nonumber
=(X-\alpha_1)(X-\alpha_2)\cdots (X-\alpha_n)\tag{2.1}
\end{align}\]
As we observed, this statement, known as the fundamental theorem of algebra, is basic to the integral calculus. It also seems, in some obscure way, to be the source of Descartes’s prophetic insistence in Sur la géométrie, 1637, on the notion of the degree of a curve but was proved only much later, as a consequence of profound reflections on the nature of what are known today as real numbers. This geometrical or topological aspect of the fundamental theorem is quite unrelated to the distinction (2.1) allows between algebraic numbers and the remaining numbers in our number system.
The notion of a group penetrates mathematics far more broadly, far more deeply than Galois theory itself
The integers 1, 2, 3… form a familiar collection of numbers. The division of a unit into a number of parts of equal length leads quickly to rational fractions, 1/2 or 1/3, 2/3, and so on, but the transition to algebraic numbers, for example, \sqrt{2} as a root of X^{2} - 2 = 0, was a major conceptual step beyond them. There are important numbers, like \pi, one-half the circumference of a circle of radius 1, that are not algebraic, but they are not our concern here. It is not immediately clear, but the sum of two algebraic numbers is algebraic, as is their product. So is their quotient if the denominator is not 0. A remarkable and fundamental theorem, although from the correct optic not difficult to prove, is that if we admit algebraic numbers as coefficients a_{i} of the equation (1.1), the roots are still algebraic.
It is not easy for a modern reader to understand the later books—for example Book X, a major contribution to the study of algebraic numbers in antiquity—of Euclid without a commentator, although I would guess that it is quite likely that much of the commentary places the mathematics in a false modern context. It already requires a great deal of imagination to penetrate the conceptual predilections of mathematicians of the previous century. For those of two thousand or more years ago an almost impossible effort is required to which, perhaps, the rewards are, for most of us, not commensurable.
As the English translator and editor Thomas Heath explains in the notes to his famous English translation, we are dealing in Book X with roots of the equations
\[\begin{align}
X^{2}\pm 2\alpha X\pm\beta=0\tag{2.1}
\end{align}\]
and
\[\begin{align}
X^{4}\pm 2\alpha X^{2}\pm\beta=0\tag{2.2}
\end{align}\]
The roots of the second equation are the square roots of those of the first, which are \pm\alpha \pm\sqrt{ \alpha^2 \mp \beta}, only those for which \alpha^2 \mp \beta \geq 0 having a meaning for Euclid. The coefficients \alpha and \beta are allowed by Euclid to be rational numbers m/n, m and n positive integers, or simple surds \sqrt{m/n}. Such equations arose in various geometric problems of Euclid’s time and later. Book X is to some extent a classification, very elaborate, of the solutions and a discussion of their nature, rational or irrational. A quite sophisticated possibility, expressed in modern terms, thus algebraically, is
\[\begin{align}
\frac{\lambda^{1/4}}{\sqrt{2}}\sqrt{1+\frac{k}{\sqrt{1+k^2}}}\pm \frac{\lambda^{1/4}}{\sqrt{2}}\sqrt{1-\frac{k}{\sqrt{1+k^2}}}\tag{2.3}
\end{align}\]
in which \lambda and k are simple fractions. The nature of this number depends on the nature of \lambda and k.
This number is the solution to Proposition 78 of Book X, given in Heath’s translation as the following problem:
If from a straight line there be subtracted a straight line which is incommensurable in square with the whole and which with the whole makes the sum of the squares on them medial, twice the rectangle contained by them medial, and further the squares on them incommensurable with twice the rectangle contained by them, the remainder is irrational; …
I have omitted a brief phrase at the end because it is irrelevant. This is a complicated statement that needs explanation. Even after its meaning is clear, one is at first astonished that any rational individual could find the statement of interest. This was also the response of the eminent sixteenth century Flemish mathematician Simon Stevin, reported by Heath as writing, “La diffculté du dixiesme Livre d’Euclide est à plusieurs devenu en horreur, matière trop dure à digérer, et en la quelle n’aperçoivent aucune utilité.” In fact, again according to Heath’s commentary, a great deal of attention was given to the book by the early algebraists, who studied in the later Middle Ages and the early Renaissance the nature of the solutions of equations of the third and fourth degree, thus equation (1.1) with n = 3, 4. The theory of Galois, which cannot be considered a complete theory, appeared only after several more centuries of reflection on equations of higher degree by major mathematicians. It is probably the principal source of the notion of a group, an indispensable ingredient, for reasons not always transparent, perhaps not even yet understood, not only of many branches of mathematics but also of much of physics, both relativity and in quantum theory. So, in spite of the explanation to follow, there is no question of dismissing Euclid’s Proposition 78 or any of the large number of similar propositions in Book X as frivolous distractions of misguided savants. There is no need to examine the explanation in detail. Enough can be learned for the present purposes simply by glancing at the formulas.
Two lines of length \tau and \tau' are incommensurable in square if their quotient squared is not a rational number. Two areas are commensurable if their quotient is rational, otherwise incommensurable. A line (read length of a line) is medial if its fourth power is rational but its square is not, a definition arising from geometrical considerations, and the area of a square is medial if its side is medial. So the proposition begins with two numbers \tau, the whole, and \sigma, the part to be subtracted, such that \sigma^{2}/\tau^{2}, \tau^{2}+\sigma^{2}, 2\tau\sigma are not rational numbers but \left(\tau^{2}+\sigma^{2}\right)^{2} and 4\tau^{2}\sigma^{2} are. The final hypothesis is that the quotient
\[\begin{align}
\frac{\tau^2+\sigma^2}{2\tau \sigma}\tag{2.4}
\end{align}\]
is irrational. The conclusion of the proposition is, in spite of the language, that (\tau -\sigma)^{2} is irrational because the word irrational as used in Heath’s translation means not irrational in the current sense but with an irrational, again in the current sense, square. Since
\[\begin{align*}
(\tau-\sigma)^2&=\left(\frac{\tau^2+\sigma^2}{2\tau\sigma}-1\right)2\tau\sigma,\\
(\tau-\sigma)^4&=(\tau^2+\sigma^2)^2-4(\tau^2+\sigma^2)\tau\sigma+4\tau^2\sigma^2.
\end{align*}\]
The first and the last terms on the right of the second equality are rational and the middle term is the product of (\tau^{2}+\sigma^{2})/2\tau\sigma and 8\tau^{2}\sigma^{2}. By hypothesis the first of these numbers is irrational and the second rational. So the sum equal to (\tau-\sigma)^{4} is irrational and, as a consequence, so is (\tau-\sigma)^{2}.
For a modern student at least, the geometric arguments of Euclid are far from transparent
We are struck here, on the one hand, by the importance the ancient Greeks attached to the distinction between rational and irrational, on the other, by the simplicity, or rather triviality, of the argument, but that is not evidence for our superior intelligence, but for the advantages of the algebraic formalism. For a modern student at least, the geometric arguments of Euclid are far from transparent. A basic construct in Book X is the apotome (“a cutting off”), expressed algebraically, basically a difference \alpha-\beta where \alpha is rational and \beta is a proper surd \beta=\sqrt{\gamma}, \gamma rational, \beta not. An example would be 1 - \sqrt{2}. It is proved in Book X as Proposition 73 that an apotome \delta=\alpha-\beta is necessarily irrational. This seems clear to us because \beta=\alpha-\delta and if \alpha and \delta were both rational, \beta would be too. The argument of Euclid is, however, quite long. Namely, as a consequence of the assumptions and of some basic, but for us formal, propositions \alpha^{2}+\beta^{2} is commensurable with \alpha^{2}, 2\alpha\beta is commensurable with \alpha\beta and as a consequence of the assumption \alpha^{2} and \alpha\beta not commensurable. Therefore (\alpha-\beta)^{2}=(\alpha^{2}+\beta^{2})-2\alpha\beta is the difference of two incommensurable quantities, one of which is irrational, and therefore irrational. Proposition 78 is proved as a consequence of Proposition 73 and, like it, is for us astonishingly elaborate.
I find the commentary of Heath somewhat imprecise, but the algebra is clear. Let \lambda=\left(\tau^{2}+\sigma^{2}\right)^{2}. It is rational. We suppose with Euclid that it is not a square. It is easy to see that for an a, 0 < a < 1,
\[\begin{align*}
\tau=\frac{\lambda^{1/4}}{\sqrt{2}}\sqrt{1+a},\quad \sigma=\frac{\lambda^{1/4}}{\sqrt{2}}\sqrt{1-a}.
\end{align*}\]
Since
\[\begin{align*}
4\tau^2\sigma^2=\lambda(1-a^2),\quad \frac{\sigma^2}{\tau^2}=\frac{1+a}{1-a},
\end{align*}\]
a is not rational but a^{2} is. Since 0 < a < 1, we may write
\[\begin{align*}
a^2=\frac{l}{1+l}
\end{align*}\]
with l rational. Let k^{2} = l, so that
\[\begin{align*}
\tau=\frac{\lambda^{1/4}}{\sqrt{2}}\sqrt{1+\frac{k}{\sqrt{1+k^2}}},\quad \sigma=\frac{\lambda^{1/4}}{\sqrt{2}}\sqrt{1-\frac{k}{\sqrt{1+k^2}}}.
\end{align*}\]
It is the difference
\[\begin{align*}
(\tau-\sigma)^2 =\frac{\lambda^{1/2}}{2}\left(\!\!{1+\frac{k}{\sqrt{1+k^2}}}-2\sqrt{1-\frac{k^2}{1+k^2}}+1-\frac{k}{\sqrt{1+k^2}}\!\!\right) = \lambda^{1/2}\left(1-\frac{1}{\sqrt{1+k^2}}\right)
\end{align*}\]
that Euclid asserts is irrational. This is so, but Heath’s commentary suggests that k will be rational and I see no reason that this is necessarily the case. If it is, then \tau-\sigma is a number of the form (2.3).
From the point of view of Galois theory, what is being examined is less the particular number (2.3) but rather a collection of numbers, called a field, formed by taking a succession of square roots and then taking all possible sums of all possible quotients of all possible products of these roots, and possibly repeating this process. In equation (2.3), we have taken the square root of \lambda to obtain \sqrt{\lambda}, then the square root of this number divided by 2 to obtain \lambda^{1/4}/\sqrt{2}. But we have also taken the square root of 1 + k^{2}, then formed the number 1 + k/\sqrt{1 + k^{2}}, taken its square root, and then taken a sum—as well as a difference—of products of the numbers obtained.
There is another theme in Book X, implicitly emphasized by the equations (2.1) and (2.2) of Heath’s commentary, namely, when for two integers \alpha and \beta is the sum \alpha^{2}+\beta^{2} or difference \alpha^{2}-\beta^{2} also an integer? This question is closely related to the equation \alpha^{n}+\beta^{n}=\gamma^{n} appearing in the famous Theorem of Fermat, in fact a problem, proposed in the seventeenth century and solved in the twentieth. It is answered in Book X, where its presence suggests a different optic than that I have stressed: not a structural analysis of the irrationalities generated by geometrical problems as in Galois theory, but simply an analysis of the dichotomy, rational–irrational, for the solutions.
The structural analysis, of the thirteenth to sixteenth century for equations of degrees three and four, of the seventeenth and eighteenth century, with the first attempts by Lagrange and others to reflect on the relations between the roots of any given equation and to stress the importance of these relations and with the sudden, largely unexpected—there were antecedents, but so far as I have been able to understand, there is no reason to think that any of his predecessors were even on the verge of his discoveries—success of a very young Gauss with the equation X^{n}-1=0, whose roots are e^{2\pi ij/n}, j=0,1,2, …, n-1, was perhaps not in any strong sense implicit in Euclid, nor was the final comprehensive theory of Galois. The problems and the notions of Euclid’s time were modified over the years but the seeds were sown then.
In the theory of Galois, the central issue is the collection of relations between the n roots of the equation (1.1) with coefficients taken from some prescribed collection. If, for example, all the coefficients are rational, the interest is in relations with rational coefficients. Consider for example the two equations,
\[X^2-2=0,\qquad X^2-4=0.\]
The first has two irrational solutions X_{1}=\sqrt{2}, X_{2}=-\sqrt{2}. The second has two rational solutions X_{1}=2, X_{2}=-2. A relation in both cases is an equality with 0 of a sum of products of powers of X_{1} and X_{2} with rational numbers, for example
\[ X_1^2-2=0, \qquad X_2^2-2=0,\qquad X_1X_2+2=0 \]
are three relations for the first equation, while
\[ X_1^2-4=0, \qquad X_2^2-4=0,\qquad X_1X_2+4=0 \]
are relations for the second. In addition, for the second equation, we have
\[X_1-2=0,\qquad X_2+2=0.\]
It is clear that there are no such simple relations for the first equation, for otherwise its roots would be rational. Another way of expressing this is that, for the first equation, we may replace in any valid relation—with rational coefficients!—X_{1} by X_{2} and X_{2} by X_{1} without invalidating it. This is clearly not so for the second. Thus there is a symmetry for the first equation, missing for the second. From the point of view of an observer familiar only with rational numbers, and in some sense that is all of us, the two roots of the first equation may be different but they are also indistinguishable, while the roots of the second equation are different and distinguishable.3 One is 2; one is -2. They add nothing new to the collection of rational numbers. For the first equation, however, the numbers aX_{1} + b = a\sqrt{2} + b are all different and, if a\ne 0, irrational. The number X_{2} appears among them as -X_{1}. This means that the collection of all numbers generated by X_{1} and X_{2}, thus the numbers of the form a + bX_{1} with a and b rational, for X_{2} can be replaced in any expression, no matter how complex, by -X_{1} and X_{1}^{2} by 2, is a larger domain (field is the better word here) than just that of the rational numbers. To have, at least conceptually, a square root of 2 we have to imagine, introduce, or construct a larger domain or field of numbers and in it, at least if the old norms and customs are maintained, there are necessarily two different roots. In the domain, and again from the point of view of the norms imposed by the customs or formalities of addition and subtraction, there are two different but indistinguishable square roots of 2. More generally a - bX_{1} = a + bX_{2} is different from a + bX_{1} but indistinguishable from it. So there is a symmetry of the domain X_{1} \rightarrow X_{2} = -X_{1} which entails a + bX_{1} \rightarrow a - bX_{1}.
Another example would be
\[X^4-5X^2+6=(X^2-2)(X^2-3)=0.\]
The roots are X_1=\sqrt{2}, X_2=-\sqrt{2}, X_3=\sqrt{3}, X_4=-\sqrt{3}. We have already observed that there is a simple relation between X_{1} and X_{2}. We might ask whether in the domain generated by X_{1}, thus in the collection of numbers aX_{1} + b, there is already a square root of 3. Thus can
\[3=(a+bX_1)^2=a^2+2abX_1+b^2X_1^2.\]
If a = 0 or b = 0 such an equation is impossible because of the theorem of Theaetetus. If b = 0 it entails 3 = a^{2}; if a = 0 it entails 6 = 4b^{2}. Both equations are impossible. If ab \ne 0, then it implies
\[X_1=\frac{3-2a^2-b^2}{2ab},\]
but that too is impossible for X_{1} cannot be rational. Thus the introduction of X_{3} entails the existence of a genuinely new domain larger than the collection of numbers a + bX_{1}. A little reflection establishes that this number is the domain a + bX_{1} + cX_{3} + dX_{1}X_{3}, which contains the square roots of 6 as \pm X_{1}X_{3}. It has three symmetries, even four,
\[X_1\to\alpha X_1;\qquad \beta X_3;\qquad X_1X_3\to \alpha\beta X_1X_3,\]
in which \alpha and \beta can be independently taken to be \pm 1. When they are both taken to be 1, the symmetry is not of great interest: objects are indistinguishable from themselves. It is useful nevertheless to introduce it for formal reasons.
These symmetries entail a permutation of the roots of the equation. Indeed they are in effect defined by a permutation of the roots, a kind of musical chairs in which the number of chairs is equal to the number of players, and in which the nature of the mixing of players and chairs at each round is circumscribed by perhaps complex rules that may nonetheless allow for madder scrambling than that customarily permitted. Permutations can be composed to form what mathematicians call a group: the result of two different rounds could clearly be the result of a single round. For many centuries equations of the form (1.1) were a puzzle. Could their roots be obtained by successive extractions of surds, thus with the help of numbers of the form \sqrt[n]{a}, with a rational or at least in the field generated by the coefficients and with n perhaps greater than 2, but nevertheless with a result along the lines of equation (2.3), typical for the problems investigated in Book X of Euclid. Galois discovered that the decisive factor in the answer was the nature of the group of symmetries, thus of the rules governing their composition. Have mathematicians abused his discovery? Since one notion appearing in Galois’s brief writings is that of a group, which is of universal importance, not alone for the theory of equations but for mathematics in general, this question may appear frivolous. To understand its sense demands some background.
Algebraic Numbers at the Beginning of the Nineteenth Century

Carl Friedrich Gauss, born in 1777, died in 1855, was a mathematician on whose contributions I have never dared to reflect seriously. He was a prodigy, but in his case the troubling connotations, almost universal among prodigious mathematicians, of early, forced efflorescence, followed by a premature withering were absent. The child of parents in modest circumstances, his talent was early remarked and he was fortunate enough to receive the support of the Duke of Brunswick.4 Thanks to the excellent education this permitted and to Gauss’s innate talent, he was at the age of eighteen, when he published in the Allgemeine Literaturzeitung, a journal founded by, among others, Goethe and Schiller and not so dissimilar to the contemporary New York Review of Books, his discovery of the possibility of the construction with only ruler and compass of a regular heptadecagon (a polygon with 17 sides of equal length and with all adjacent sides meeting at the same angle), already a mature mathematician. Whether such a construction was possible was a problem that had remained unsolved for two thousand years, longer than the impossibility of duplicating the cube or trisecting a general angle, both difficult but easier problems to which it is nonetheless similar, and almost as long as the question of the squaring of the circle, which is analyzed by quite different considerations.
I have found over the course of the years, without making any particular effort, that the more one penetrates Gauss’s writings the closer one comes to mathematics
Gauss’s career began on the threshold of the nineteenth century, and it is instructive to begin a discussion of it with a brief description of two key contributions that influenced the mathematics of that century in very different ways. I have found over the course of the years, without making any particular effort, that the more one penetrates Gauss’s writings the closer one comes to mathematics. His early writings manifest youthful force and the pleasure in detail it allows and at the same time a mature, critical understanding of the contributions of his predecessors and the problems they faced. Whether he was always just to them, I cannot say, but his primary concern seems to have been not to seize fame but to grasp the essence of a question.
I observe in passing that attention to detail is not a luxury even when occupied with the most abstruse questions, but contemporary mathematicians, including those of my generation, usually start late and have a great deal to master. So willy-nilly we remain superficial. I see no obvious remedy except too sharp a focus and that is worse.
Gauss’s Disquisitiones Arithmeticae, published in 1801 when he was 23, was the foundation and the inspiration of algebraic number theory, one of the great nineteenth-century achievements of mathematics and was the source not only of Galois’s inspirations but of the quite different contributions of a number of the century’s great number theorists. The seventh and last chapter was the beginning of the theory of cyclotomy, thus of the division of the circumference of a circle into n equal parts and, thus, the construction of regular polygons with n sides. It is a question whose relation to beauty is immediate and, if one were so inclined and had the necessary competence, it would be appropriate at this conference to devote a full lecture to it, but I introduce it only as one aspect of a much larger question.
The geometric problem, which is to construct these figures with a ruler and compass, had already been considered by the Greeks and is the principal topic of Euclid’s Book IV, where regular polygons of 3, 4, 5, 6, and 15 sides are treated. The geometric problem is, at its core, algebraic. If we allow ourselves the freedom of using complex numbers, thus numbers x + y \sqrt{-1} = x + yi represented by points (x, y) in the plane, then the vertices of a regular polygon of n sides inscribed in a circle of radius r with center at the origin of coordinates are represented by the complex numbers \cos(2\pi/k) + \sin(2\pi/k)i, k=1,2,…, n-1. Taking the radius as the unit of length, these are for a triangle 1+0\cdot i=1, \cos(2\pi/3) + \sin(2\pi/3)i=-1/2+\sqrt{3}i/2, \cos(2\pi/3)-\sin(2\pi/3)i = -1/2-\sqrt{3}i/2, because \cos(2\pi/3) = -1/2 and \sin(2\pi/3) = \sqrt{3}/2. As points in the plane these are (1,0), (-1/2, \sqrt{3}/2), (-1/2, -\sqrt{3}/2). For a pentagon, we take again one of the vertices to be (1, 0), then the others are
\[\begin{align}
(\cos(2\pi/5),\sin(2\pi/5))&=\left(\frac{-1+\sqrt{5}}{4},\sqrt{\frac{5}{8}+\frac{\sqrt{5}}{8}}\right)\nonumber \\
(\cos(4\pi/5),\sin(4\pi/5))&=\left(\frac{-1-\sqrt{5}}{4},\sqrt{\frac{5}{8}-\frac{\sqrt{5}}{8}}\right)\nonumber \\
\tag{3.1} \\
(\cos(6\pi/5),\sin(6\pi/5))&=\left(\frac{-1-\sqrt{5}}{4},-\sqrt{\frac{5}{8}-\frac{\sqrt{5}}{8}}\right)\nonumber \\
(\cos(8\pi/5),\sin(8\pi/5))&=\left(\frac{-1+\sqrt{5}}{4},-\sqrt{\frac{5}{8}+\frac{\sqrt{5}}{8}}\right).\nonumber
\end{align}\]
These two regular polygons appear in Figures I and II. We see in (3.1) a phenomenon with which we are familiar: with the expressions in which there is a square root appear simultaneously the expressions in which the sign of this square root is reversed. This is a manifestation of the Galois symmetry among the roots of the algebraic equation satisfied by the complex numbers yielding the vertices of the pentagon, namely
\[(X-1)(X^4+X^3+X^2+X+1)=X^5-1=0.\]
The same phenomenon for the triangle is less striking because the equation is
\[(X-1)(X^2+X+1)=X^3-1=0,\]
and we have perhaps seen too many quadratic equations.
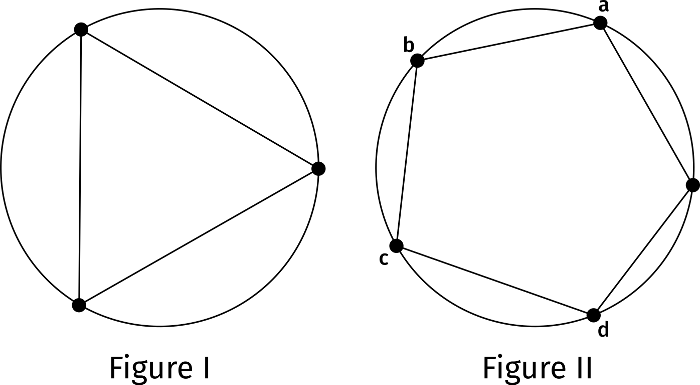
Nevertheless it is best when beginning to reflect on the symmetries of the two equations
\[X^4+X^3+X^2+X+1=0,\qquad X^2+X+1=0,\]
to consider them simultaneously. The algebraic symmetries are not the geometric symmetries, thus not the obvious rotational symmetries of the triangle or the pentagon. For the triangle, the algebraic symmetry is the absolute indistinguishability from an algebraic standpoint of the two roots -1/2 \pm \sqrt{3}i/2. The symbol i is just that, a symbol, thus a convention that we have learned to accept as having a real meaning, as it may have, but in its intrinsic mathematical properties it is indistinguishable from -i. For the quadratic equation X^{2} + X + 1 = 0 one might dismiss this distinction as pedantic logic-chopping, but for the first equation, that of degree four, the significance is not to be denied. There are five rotational symmetries for the pentagon, those through angles 2\pi/5, 4\pi/5, 6\pi/5, 8\pi/5 together with the trivial rotation, which is always present. There are also five reflections that preserve the pentagon. There are only four algebraic symmetries and they cannot easily be represented geometrically. The four roots of X^{4} + X^{3} + X^{2} + X + 1 = 0 are listed in (3.1): a = \cos(2\pi/5) + i \sin(2\pi/5); b = \cos(4\pi/5) + i \sin(4\pi/5); c = \cos(6\pi/5) + i \sin(6\pi/5); d= \cos(8\pi/5) + i \sin(8\pi/5). These four roots determine a field of numbers, those numbers that can be formed by adding rational multiples of these four,
\[ \alpha a+\beta b+\gamma c+\delta d, \]
where the coefficients \alpha, \beta, \gamma, \delta are rational numbers. As a simple example we could take \alpha = \beta = \gamma = \delta = 1, but that yields a + b + c + d which is easily verified to be -1. Different coefficients lead to different numbers and it is difficult to gain any geometric insight into their totality. It is however easily verified that the sum or the difference of two such numbers is again such a number, as is the product or a quotient. It is this possibility of forming sums, differences, products and quotients within a given collection of numbers that mathematicians express by referring to the collection as a field, a word that we have used more than once already but without making its meaning precise. The Galois symmetries are symmetries of the field. For example, if a is replaced by a_{1} = b, then b is replaced by b_{1} = d, c by c_{1} = a, and d by d_{1} = c. All algebraic relations are preserved, a^{2} = b entails a_{1}^{2} = b_{1} or ab = c entails a_{1}b_{1} = c_{1}. The consequences of this are not immediately apparent.
We can guess, if we have any familiarity with complex numbers, that for other possible integers n, the equation
\[(X-1)(X^{n-1}+\cdots +X+1)=X^n-1=0\]
is pertinent to the construction of a regular polygon with n sides. It is best when first examining the equation to treat prime numbers n, thus n = 3, 5, 7, 11, 13, 17,…. There are again n solutions, of which the first, 1 + 0 \cdot i, or, in the plane, the point (1, 0) corresponds to the arbitrarily assigned first vertex. The problem is to construct the others once it is given, thus to construct geometrically the angle 2\pi/n. That depends on the symmetries, or, as we would now say, the Galois symmetries of the n -1 roots, \theta_{i} = \cos(2\pi k/n) + \sin(2\pi k/n)i of the equation
\[\begin{align}
\tag{3.2}
X^{n-1}+\cdots +X+1=0.
\end{align}\]
At this point, I have to rely on you to recall from basic trigonometry two identities that are at the core of any treatment of equation (3.2),
\[\begin{align}
\cos(2\pi k/n)\cos(2\pi l/n)-\sin(2\pi k/n)\sin(2\pi l/n) &=\cos(2\pi(k+l)/n),\nonumber \\
\tag{3.3} \\
\cos(2\pi k/n)\cos(2\pi l/n)+\sin(2\pi k/n)\cos(2\pi l/n) &=\sin(2\pi(k+l)/n).\nonumber
\end{align}\]
As a consequence \theta_{k} \theta_{l} = \theta_{k+l} if k + l < n. It is 1 if k + l = n and \theta_{k+l-n} if k + l > n. It has to be proven, but from an algebraic point of view, that all the numbers \theta_{k} are indistinguishable. In so far as only equations with rational coefficients are admitted, they satisfy exactly the same equations. Moreover all of them can be represented as algebraic expressions of any given one, for example, as a consequence of the identities (3.3), \theta_{j} = \theta_{1}^{j}, or if l - kj is a multiple of n, \theta_{l} = \theta_{k}^{j}. So, in principle, we understand the Galois theory of the equation (3.2), as Gauss did before Galois was born. The symmetries, in other words, the permutations of the roots that preserve all relations between them, are determined by \theta_{1} \rightarrow \theta_{k}. Thus \theta_{1} is replaced by \theta_{k}, where k can be any integer from 1 to n - 1, and then \theta_{j} is necessarily replaced by \theta_{1}^{l}, where l - kj is divisible by n.
We seem to be losing our way. The initial question, a question that presumably confronted the Hellenistic mathematicians but was abandoned by them as too difficult, was whether for other integers than those n appearing in Book IV of Euclid, it is possible to construct with ruler and compass, thus by the successive extraction of square roots, regular polygons with n sides. For which n can \theta_{1} = \cos(2\pi/n) + \sin(2\pi/n)i be represented as an expression similar to those in (3.1). This imposes some conditions on the possible algebraic symmetries of the equation, which form what came to be called the Galois group.
Each time we add a square root, thus each time we perform a construction with ruler and compass, we enlarge the field generated by the roots, and as a result of the general theory there will be additional symmetries, those already there together with one that replaces the newly adjoined square root by its negative. Thus when concretely expressed the elements of the Galois group will have to appear simply as sign changes. This means, to make a long story short, that the total number of permutations will be a power of 2. We have seen that for the field of numbers of concern to us the number of permutations is n - 1. It does not happen very often, for n a prime, that this number is a power of 2. It is true for n = 3, n - 1 = 2, and, as the equations (3.1) make explicitly clear, also for n = 5, n - 1 = 4 = 2^{2}. The next possibility is n = 17, n - 1 = 16 = 2^{4}, and the consequences were understood only after two thousand years. As one infers from its publication in the Allgemeine Literaturzeitung, the possibility of constructing a regular heptadecagon was expected to astound not only mathematicians but the entire educated world. It astonishes mathematicians to this day. Much as I admire the achievement and the style of Galois, and troubled as I am by any exaggerated admiration of Gauss, I find that any judgement of the nature of Galois’s achievement has to be preceded by a sober reflection on what Gauss had already accomplished.
Any judgement of the nature of Galois’s achievement has to be preceded by a sober reflection on what Gauss had already accomplished
A complete analysis of the Galois theory of the equation
\[\begin{align*}
X^{16}+X^{15}+X^{14}+X^{13}+X^{12}+X^{11}+X^{10}+X^{9}\quad
+X^{8}+X^{6}+X^{5}+X^{4}+X^{3}+X^{2}+X+1=0,
\end{align*}\]
important because
\[\begin{align*}
(X-1)(X^{16}+X^{15}+X^{14}+X^{13}+X^{12}+X^{11}+X^{10}
+X^{9}+X^{8}+X^{6}+X^{5}+X^{4}+X^{3}+X^{2}+X+1)
\end{align*}\]
is equal to X^{17} - 1, would be out of place. A basic root is \theta = \cos(2\pi/17) + \sin(2\pi/17)i. The symmetries are \theta \rightarrow \theta^{k}, k = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16. There are sixteen of them. The first, for k = 1, is simple, \theta \rightarrow \theta. The second
\[\theta\to\theta^2,\quad \theta^2\to\theta^4,\quad \theta^4\to\theta^8,\quad \theta^8\to\theta^{16},\]
and continuing, because, for example \theta^{16} = \theta^{-1} and the square of \theta^{-1} is \theta^{-2} = \theta^{15},
\[\theta^{16}\to\theta^{15},\quad \theta^{15}\to\theta^{13},\quad \theta^{13}\to\theta^9,\quad \theta^9\to \theta,\]
which gives only eight in all because we return to the initial point. If we had started with \theta \rightarrow \theta^{3}, which is missing from this list of eight, we would have
\[\begin{align}
\theta\to\theta^3&\to\theta^9\to\theta^{10}\to \theta^{13}\to\theta^5\to \theta^{15}\to\theta^{11}\to\theta^{16}\nonumber \\
\tag{3.4} \\
&\to\theta^{14}\to\theta^8\to\theta^7\to\theta^4\to\theta^{12}\to\theta^2\to\theta^6\to\theta.
\nonumber
\end{align}\]
We return at the end to the initial point, generating on the way all 16 possible roots. The group of symmetries has 16 elements and is generated by a single one, that which replaces \theta by \theta^{3}.
We can construct from these diagrams, step by step, combinations of the roots that are less and less symmetric. A very symmetric combination is obtained by adding together all the roots. It is equal to -1. If we just add together every second root in (3.4), we obtain
\[ \theta+\theta^9+\theta^{13}+\theta^{15}+\theta^{16}+\theta^8+\theta^4+\theta^2 \]
or
\[ \theta^3+\theta^{10}+\theta^{5}+\theta^{11}+\theta^{14}+\theta^7+\theta^{12}+\theta^6. \]
These numbers look very complicated but a patient calculation and appropriate use of the equation
\[ X^{16}+X^{15}+\cdots +X^2+X+1=0\]
satisfied by \theta establish that the first is equal to (-1+\sqrt{17})/2 and the second to (-1-\sqrt{17})/2. We can continue with the combinations
\[\theta+\theta^{13}+\theta^{16}+\theta^4, \qquad \theta+\theta^{16}, \qquad \theta,\]
each in some sense one-half as symmetric as the previous one, with respect to which it satisfies a quadratic equation, arriving finally at the expression
\[\begin{align*}
-\frac1{16}+\frac 1{16}\sqrt{17}+\frac 1{16} \sqrt{34-2\sqrt{17}}\hskip 1.25in{}
+\frac18\sqrt{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}},
\end{align*}\]
for \cos(2\pi/17). It is complicated with three telescoping square roots. The number
\[\sin(2\pi/17)=\sqrt{1-\cos^2(2\pi/17)}\]
requires one more square root. Thus we need four in all, together with that for i=\sqrt{-1}, to express \theta. It is worthwhile to ask oneself how an eighteen-year-old might have felt on writing down these equations, the solution of a problem more than two thousand years old.
For reasons of convenience, Gauss wrote a thesis that contained neither this theorem nor any of the other major discoveries from which the modern theory of numbers developed. The central feature of the thesis is a proof of the fundamental theorem of algebra, which we have already encountered. I repeat, with a different emphasis, its enunciation, both in a modern form and in the form for which Gauss offered at the age of 20 a proof, sometimes considered as the first proof, although I think it is fairer to say that Gauss was, even though the initiator, just one of the architects of the proof or proofs, which ultimately rely on a very sophisticated understanding of the nature of a real number that was unavailable at the end of the eighteenth century. Gauss himself published over the course of several years four different proofs.5
The notion of a real number has an immediate intuitive basis in our notion of distance. So I take it as undefined, but in fact its formal mathematical definition demands considerable preliminary reflection. The real numbers available, a complex number is taken to be a formal object of the form a + b\sqrt{-1}, where a and b are arbitrary real numbers. Two equivalent statements of the fundamental theorem of algebra are that any polynomial with complex coefficients, the first being 1, factors as a product of linear polynomials
\[X^n+aX^{n-1}+\cdots +f X+g=(X-\alpha_1) (X-\alpha_2)\cdots (X-\alpha_n)\]
with complex numbers \alpha_{i} or that any polynomial with real coefficients factors as a product of linear factors and quadratic linear factors, all coefficients being real,
\[\begin{align*}
X^n+aX^{n-1}+\cdots +f X+g=(X-\alpha_1)\cdots \hskip .5in
(X-\alpha_k)(X^2-\beta_1 X+\gamma_1)\cdots (X^2-\beta_l X+\gamma_l),
\end{align*}\]
k+2l=n. It is the second form that Gauss proved.
His first proof is of interest even today, simply as a mathematical proof taken by itself, regardless of the historical interest or scientific implications of the theorem. Moreover it is preceded by a review of the proofs, or attempts at proofs, by earlier authors. He points out their errors systematically. One observation I find curious. Apparently earlier authors, who are not named, were willing to accept the possibility that a polynomial like
\[X^n+aX^{n-1}+\cdots +fX+g=0\]
had fewer than n complex roots, even if they were counted with the correct multiplicities.
They were unwilling to abandon the missing roots and proposed to introduce them—somewhat along the lines, I suppose, of i = \sqrt{-1}—as impossible roots. Gauss found, for reasons I cannot understand, such a step inadmissible. We know today that if the fundamental theorem of algebra were false it would be possible, and certainly legitimate, to include within the formalism of mathematics a larger collection of “numbers” that permitted the desired factorization of polynomials. The fundamental theorem is true however. So this larger collection is unnecessary. No new numbers are necessary to account for the impossible roots.
What if the fundamental theorem had been false? Although he was, almost two hundred years before Gauss, in no position to express himself clearly, for Descartes the fundamental theorem of algebra is a fundamental theorem of geometry. The number of points at which two curves each of some fixed algebraic form, for example two conics, meet depends only on these forms. This is a consequence of the fundamental theorem of algebra. If the fundamental theorem of algebra were false, there would be the “true” Cartesian geometry, in which there were only complex numbers, but in which Descartes principle was false, and a formal, algebraic one, in which it was valid. The true one would be the one deduced from geometry and from our geometric notions based on the relation between number and distance; the formal one would be one in which the impossible numbers were granted legitimacy. However, Descartes principle,6 thus the fundamental theorem of algebra as the fundamental theorem of geometry, is intimately linked to the possibility of introducing topological invariants into geometry. We now know, thanks to an insight of André Weil in 1949 and to the very elaborate theory of algebraic geometry created by many, many practitioners over the nineteenth and twentieth centuries, that their introduction would have also been possible, at least to some extent, in the formal, algebraic theory alone, without reference to the concrete geometry informed by our intuitive notions of distance and number, but this would have been a difficult route to take. Fortunately it was not necessary. Pure mathematicians were permitted for a very long time to rely on their geometric intuition and still are. Some preparation is necessary before we can begin to appreciate the—strange and still mysterious—modern relation between algebra and geometry, much more abstruse than in Euclid.
Algebraic Numbers during the Nineteenth Century
Thanks to the influence not only of his study of cyclotomy but also of the many other varied, but all basic, early contributions of Gauss to the solution of outstanding unsolved problems of late eighteenth-century number theory, a general theory of algebraic numbers was created in the course of the nineteenth century, initially in order to search, in part successfully, for a proof of the famous theorem of Fermat, to the effect that for n > 2, there are no integral solutions to the equation
\[\begin{align}
X^n+Y^n=Z^n, \qquad XYZ\ne 0. \tag{4.1}
\end{align}\]
It was observed, in particular by the German mathematician E.E. Kummer, whose central concern it became, that the problem is related to a notion already appearing in connection with Theaetetus, that of prime and that of the unique decomposition of an arbitrary number into primes, thus 30 = 2 \times 3 \times 5. For example, when n is a prime the possibility of unique factorization into primes in the domain of numbers
\[\begin{align}
a_0+a_1\theta+\cdots +a_{n-2}\theta^{n-2}+a_{n-1}\theta^{n-1},\qquad\nonumber
\theta=\cos\left(\frac{2\pi}{n}\right)+i\sin\left(\frac{2\pi}{n}\right),
\tag{4.2}
\end{align}\]
where the coefficients a_{0}, a_{1},… are taken to be rational, is the key to the impossibility of finding a solution to (4.1). It turns out, however, that for some n this is possible, and for some n it is not. This entailed complications and decades of effort by some very strong minds.7
The mathematical concept of ideal is now commonplace, but it was difficult to arrive at

Rather than continuing with cyclotomic domains, I describe a simple example taken from a presentation of the basic ideas of the theory of algebraic numbers by one of its creators, Richard Dedekind. To study the solution in integers or in rational numbers of an equation like (4.1), referred to for historical reasons as diophantine equations, it is usually imperative to enlarge the possibilities and to study it not only in domains given by algebraic numbers, like that given by the numbers (4.2), or, as a simpler example, by the numbers a + b \sqrt{-5} = a + b\theta, a, b rational, \theta^{2} = -5. For this one needs to be able to factor them into prime factors, more precisely, just as it is ordinary integers and not fractions that we customarily factor, it is best to consider the factorization of elements in the new domain that can be regarded as analogues of ordinary integers. The appropriate definition is subtle but, in the present case, the result is simple. A number of the form \alpha = a + b\theta, a, b rational, is to be regarded as integral if a and b are integers. These factors have now often to be ideal prime factors, but the factorization has still to be unique. Let 𝜊 be the collection of integral elements a + b\theta.
Dedekind considers the question of whether there are primes in this domain and whether every number can be factored in an essentially unique way into a product of primes. As we shall see it cannot. To deal with the consequent difficulties, in particular, to undertake the investigation of Fermat’s theorem along the lines proposed by Kummer, it is necessary to introduce the notion of ideal primes and, to some extent as a terminological convenience, ideal numbers. In spite of the name, usually abbreviated to ideal in the singular and ideals in the plural, these are objects that exist within the accepted mathematical formalism and that are of great use not only in number theory but in other domains as well, in particular in geometry. They are not, however, numbers! The mathematical concept of ideal is now commonplace, but it was difficult to arrive at.
Notice that (a + b\theta)(c + d\theta) = (ac -5bd) + (bc + ad)\theta is a number of the same form. Thus we can, indeed, take products of these numbers. We introduce, as an aid to our reflections the norm of these numbers, N \alpha = a^{2} + 5b^{2}, \alpha = a + b\theta, noting that N \gamma = N \alpha N \beta when \gamma = \alpha\beta and that N \alpha = 1 only for \alpha = \pm 1. Just as for ordinary integers, an element \alpha of 𝜊 may or may not be decomposable as a product \alpha = \beta\gamma. Such a decomposition is interesting only if neither \beta nor \gamma is \pm 1. At first glance it is tempting to take a number to be prime if it is not decomposable.
Dedekind considers, with this in mind, the following numbers a = 2, b = 3, c = 7, and
\[\begin{align*}
b_1&=-2+\theta, & b_2&=-2-\theta; & c_1&=2+3\theta, &\!\!\! c_2&=2-3\theta; \\
d_1&=1+\theta, & d_2&=1-\theta; & e_1&=3+\theta, &\!\!\! e_2&=3-\theta; \\
f_1&=-1+2\theta, & f_2&=-1-2\theta; & g_1&=4+\theta, &\!\!\! g_2&=4-\theta.
\end{align*}\]
For these numbers we have N a = 4, N b = 9, N c = 49, and for the norms of the others
\[\begin{array}{llll}
9,&9,&49,&49; \\
6,&6,&14,&14; \\
21,&21,&21,&21.
\end{array}\]
If any of these numbers factored as a product \omega\omega', with neither \omega nor \omega' equal to \pm 1, then necessarily N \omega > 1 and N \omega' > 1, and thus necessarily both of these numbers are equal to one of 2, 3, 7. These three numbers are clearly not representable as x^{2} + 5y^{2}, with x and y integral. So we have several, namely 15, indecomposable numbers available, and as the following table indicates, we can find products among them that are equal. So unique factorization is out of the question.
\[\begin{array}{crl}
ab=d_1d_2, & b^2=b_1b_2, & ab_1=d_1^2, \\
ac=e_1e_2, & c^2=c_1c_2, & ac_1=e_1^2, \\
bc=f_1f_2=g_1g_2, & af_1=d_1e_1, &ag_1=d_1e_2.
\end{array}\]
Dedekind observes, indeed it is evident, that all these equalities are compatible with the existence of factorizations,
\[a=\alpha^2, \qquad b=\beta_1\beta_2, \qquad c=\gamma_1\gamma_2;\]
and
\[\begin{array}{llll}
b_1=\beta_1^2,\quad &b_2=\beta_2^2;\quad & c_1=\gamma_1^2, \quad &c_2=\gamma_2^2;\\
d_1=\alpha\beta_1,\quad &d_2=\alpha\beta_2;\quad & e_1=\alpha\gamma_1, \quad &c_2=\alpha\gamma_2; \\
f_1=\beta_1\gamma_1,\quad &f_2=\beta_2\gamma_2;\quad & g_1=\beta_1\gamma_2, \quad &c_2=\beta_2\gamma_1;
\end{array}\]
and then continues to show the existence of ideals (ideal numbers) that yield these identities, but the search for the correct concepts preoccupied Dedekind—and Kronecker—for a lifetime. Although over time, various mathematicians have expressed a preference for Kronecker’s treatment, it appears to me that Dedekind’s resolution of the problem—in which an ideal number is a set in the modern mathematical sense—has prevailed. In the basic theory of algebraic numbers established in the last decades of the nineteenth century, entirely new problems were posed and a new theory proposed, now referred to as class field theory, with decisive suggestions from Kronecker, Weber, and Hilbert, and then solved in the early decades of the twentieth century by Fürtwangler, Takagi and Artin. These were all outstanding mathematicians, but it is probably the name of David Hilbert and his intimate involvement with the theory that offers to non-mathematicians, or even to mathematicians with no special knowledge of algebraic numbers, the most credible guarantee of its interest. The subject was, nevertheless, largely neglected in the early post-war years, partly because it had been sustained principally by German mathematicians and the mathematical strength of Germany did not survive the war, partly because of internal exhaustion. It is instructive to recall the words of Emil Artin, who had emigrated to the USA and who was not only a major contributor to the subject in the 1920s but also, I should think, the mathematician principally responsible for introducing the subject to the new world, to the Princeton Bicentennial Conference on Problems of Mathematics, a gathering of very many, very distinguished mathematicians in 1946. After recalling a theorem of Richard Brauer and stating that it represents a decisive step in the “generalization of class field theory to the non-Abelian case, which is commonly regarded as one of the most diffcult and important problems in modern algebra”, the report of the conference cites Artin, one of the participants, as observing, “My own belief is that we know it already, though no one will believe me—that whatever can be said about non-Abelian class field theory follows from what we know now, since it depends on the behaviour of the broad field over the intermediate fields—and there are sufficiently many Abelian cases.”
In the next few lines, I shall describe the Abelian theory but only very briefly before turning to other domains, less abstruse and known to broader classes of mathematicians and scientists, where the influence of the theory of algebraic numbers has been decisive, but often forgotten, and which have had an essential influence on the beginnings of theories that are expected to contain the sought for non-Abelian theory. It is still premature, however, to attempt to assess the prophetic significance—or lack of it—in Artin’s words. The immediate lesson is the importance or, better, the value in the search for theorems of some profundity or for the theories in which they are implicit of escaping the confines of any particular speciality.
At this point, the reader has perhaps enough experience to appreciate more precisely of what Galois’s ideas consisted. We have introduced domains of numbers, technically referred to as fields, that are obtained by taking some fixed algebraic number \theta, a root of an equation of the form (1.1) with rational coefficients a_{0}, a_{1}, …. It will then satisfy a unique such equation of lowest degree, say n and the fields are then the collection of numbers of the form \alpha_{0} + \alpha_{1}\theta + \alpha + 2\theta^{2} + \cdots + \alpha_{n-1}\theta^{n-1}. As we have observed, the sum or difference of two numbers with such a representation again has one, as does the product, and the quotient provided the denominator is not 0. It is very advantageous to assign this domain, which is a collection or set of numbers a label, say k or K. The first is contained in the second, k \subset K, if every element of the first is also an element of the second. A simple example of this is to take k to be the collection of numbers a + bi, i^{2} = -1, a and b rational and K to be the numbers a+b\theta+c\theta^{2}+d\theta^{3}, where
\[\theta=\cos\pi/4+i\sin \pi/4=1/\sqrt{2}+i/\sqrt{2}.\]
The object of Galois theory is such pairs K/k. There is one kind of pair that is especially important in the context of that theory. K is called a Galois extension of k if when K contains \eta and the element \mu is such that every equation of the form (1.1) with coefficients a_{0},…, a_{1} from k that has \eta as a root also has \mu as a root, then K also contains \mu. For example, if k is the field of rational numbers and K is the field of numbers a_{0} + a_{1}\theta +\cdots + a_{16}\theta^{16}, \theta = \cos 2\pi/17 + \sqrt{-1} \sin 2\pi/17 that plays a central role in the study of the heptadecagon then K/k is a Galois extension. K is also a Galois extension of the field k' formed from the numbers a_{0} + a_{1}\sqrt{17}, a_{0} and a_{1} rational. This we discovered implicitly when examining Gauss’s construction of the heptadecagon. The number \mu is in general called a conjugate of \eta over k.
Whatever beauty the symmetries expressed by these correspondences have, it is not visual
The basic affrmations of Galois theory as created by Galois are that if K/k is a Galois extension then we can find an element \eta of K and an integer n such that, first of all, every element of K can be written uniquely as a sum \alpha_{0} + \alpha_{1}\eta + \alpha_{2} + \eta^{2} + \cdots + \alpha_{n-1}\eta^{n-1}, secondly that \eta has exactly n conjugates \mu, including itself; thirdly that for each of these conjugates \mu the correspondence
\[\begin{align*}
\phi: a_0+a_1\eta+a_2\eta^2+\cdots +a_{n-1}\eta^{n-1} \longrightarrow a_0+a_1\mu+a_2\mu^2+\cdots +a_{n-1}\mu^{n-1}
\end{align*}\]
preserves all algebraic relations. These correspondences can be composed and form what is called a group, the Galois group. What cannot be sufficiently emphasized in a conference on aesthetics and in a lecture on mathematics and beauty is that whatever beauty the symmetries expressed by these correspondences have, it is not visual. The examples described in the context of cyclotomy will have revealed this.
Galois theory became, together with the theory of ideals, a central guiding feature of the study of algebraic numbers in the nineteenth century and continues to inform a great deal of number theory, especially the theory of diophantine equations.
The Galois groups encountered in the theory of cyclotomy are, as we have seen in the examination of specific cases although without explicitly drawing attention to it, rather special. They are abelian, in the sense that when we compose any two of the correspondences to obtain a third, the order in which the correspondences are applied does not matter. A decisive observation of Leopold Kronecker was that, when k is the field of rational numbers itself, abelian Galois groups appear only for cyclotomic fields K and for fields K lying within them, thus only for those fields that arise in the study of regular polygons. The problem then was posed in various forms, which became increasingly precise, whether it would be possible over any field k of algebraic numbers to describe all the abelian Galois extensions. Although I have no intention of presenting it in detail here, this description was achieved and in connection with an apparently unrelated phenomenon, the decomposition of primes in k in a larger field K, but only for K/k Galois with an abelian Galois group. This is a problem to which over the course of the nineteenth century Gauss, Dirichlet, Dedekind and Frobenius had contributed.
We can already see the phenomenon in Dedekind’s example, for which the field k is the field of rational numbers and K the field of numbers a + b \sqrt{-5} with a and b rational, a field that arises in connection with the construction of a regular polygon with 20 sides and that is closely related to the field containing the numbers (3.1). Continuing the calculations of Dedekind, we could ask ourselves what ideals in k, thus what prime numbers p= 2, 3, 5, 7, 11, 13, 17, 19, … are the products of two prime ideals in K in the sense for which this is true for 3 and 7 in Dedekind’s explanatory calculations and which, like 11, 13, 17, 19, remain prime, in the sense that such factorizations are not possible. It turns out that, apart from 2 and 5 which are exceptional, the distinction is determined by the remainder left on division by 20. If it is 1, 3, 7 or 9 such a factorization is possible; if it is 11, 13, 17 or 19 it is not. The core of class field theory and the key to Kronecker’s discovery, striking in its time and striking today, is that these two phenomena are intimately related.
Can the revelation of these arcane properties of numbers, their factorizations, in what-ever sense, and their relation to the structure—abelian or non-abelian—of a group with no apparent visual appeal in any sense be considered beautiful? Of what value is it? It certainly lacks the immediate appeal of elementary geometry and arithmetic or indeed of simple algebra, which can fascinate even a child; it is also a far cry from the sharpening of our sensuous pleasure in fluid flow or other kinds of movement offered by its description in terms of differential equations and their solutions. On the other hand, these matters are less recondite than they at first seem and remain reasonably close to their origins in the reflections of eighteenth century mathematicians like Euler, Legendre and Gauss on more immediate properties of the integers, and are certainly essential for the understanding of Fermat’s theorem, for a long time the favourite puzzle of amateur mathematicians and of many professionals. Class field theory and related matters have become the stock in trade of a very large number of professional mathematicians, so that the question of its value is an existential question, best avoided.
Notes
-
The mathematician Theaetetus is famous for his understanding that the square roots of numbers like 2, 3 and 5 are irrational, but this, although briefly mentioned at the beginning of the lengthy epistemological dialogue, is not particularly relevant to its discussion of the nature of knowledge. Presumably Plato chose a well-known mathematician as Socrates’s interlocutor and mentioned his principal accomplishment in part for a reason not so dissimilar to one of mine for introducing a Platonic dialogue: to provide a little colour!
These lines were in the text prepared in connection with the lecture at Notre Dame even before I came to the conference, although I did not reach them in the talk itself. At Notre Dame, I had a brief conversation with Kenneth Sayre, from whom I learned that the introduction of Theaetetus not only into the dialogue that bears his name but into the next dialogue, the Sophist, had more serious literary purposes than I, in my innocence and ignorance, had imagined. These are clarified in his book Plato’s Literary Garden.
It would be presumptous for me to comment on the force of Plato’s use of quadratic surds as epistemological metaphors. I do not have the experience to say with any confidence that I have an inkling of how they might have been understood by Plato; nor do I have the courage to pursue the metaphor in a modern context, although that would not be ridiculous, for the study of quadratic and higher surds continues to be of fundamental importance for the theory—class field theory, that occupies a central position in Diagram A—and in pure mathematics. One of the first appearances of quadratic surds in a novel, modern way is in Gauss’s theory of binary quadratic forms, which was followed a hundred years later by a similar theory for higher surds that, according to the once very familiar, but now little read although still important, 1925 report of Helmut Hasse den Kernpunkt des ganzen Gedankenganges (of class field theory) bildet. There are, I believe, in this connection still critical issues to be resolved. I shall return to them in a later section.
- Galois died in 1832 at the age of twenty-one in what is often considered to be a duel with a ruffian but looks very much to me as though it could have been an assassination by agents of Louis-Philippe. So far as I know the circumstances of his death have never been examined critically by any one familiar with the methods of the secret police in the July Monarchy or with the government’s stand with regard to uncompromising revolutionary elements.These lines, too, were in the text before I came to the conference, although, again, I did not reach them in the talk itself. During the course of the conference, Mario Livio drew my attention to his book The Equation That Couldn’t Be Solved, to the wealth of biographical material, new and old, on Galois that it contains, and to his own reflections on the material and its import. Even without the appeal of Galois’s reputation as a mathematician, it would be instructive, I believe, to have the comments on his political activities and his death of someone thoroughly familiar with social conditions in France at the time of the July revolution and with a detailed understanding of internal security under Louis-Philippe.
- Those familiar with the square root i of -1 and its role in complex analysis are perhaps accustomed to distinguishing between i and -i, because in the customary geometric representation, i is above the axis of real numbers and -i below it. This is an illusory distinction, although mnemonically of great convenience in geometric arguments.
- The Duchy was very small. It is fascinating, but no doubt idle, to reflect on the extent to which Gauss’s native ability was favored by fortuitous circumstances. He was remarkably fortunate, for he drew himself in the Duchy’s schools not only to the attention of his teacher, J.G. Büttner, but also to that of his assistant, Martin Bartels, only eight years older than Gauss himself. It is not clear how much he may have learned from Bartels, but in such circumstances a little goes a long way and the early acquaintance with Bartels, who went on to a distinguished career as professor of mathematics in Reichenau, Dorpat and Kazan, was likely to have been decisive in Gauss’s intellectual development. Both G.W. Dunnington, the author of Gauss, Titan of Science (1954) and W.K. Bühler, the author of Gauss, A Biographical Study (1981), perhaps the two best known Gauss biographies, seem to me singularly insensitive to the value to an adolescent of even a very brief introduction to intellectual possibilities, let alone that of sustained intercourse over a period of years. I am also taken aback by Bühler’s suggestion that someone of Gauss’s mathematical distinction might have difficulty learning Latin or Greek. It is instructive to compare Gauss’s early career with that of his near contemporary, the geographer Karl Friedrich von Klöden, born in 1786 in Berlin, who describes his own genuinely impoverished childhood and early career in his once fairly widely read Jugenderinnerungen, but this is a matter of social history.
In descriptions of Gauss’s achievement, his excellent early education and his early introduction to serious mathematics by highly competent teachers is obscured, in hopes, perhaps, of dazzling innocent readers. Gauss himself, with the occasional convenient reticence, may—or may not—have been complicit in the deception, but not in any very troubling way. Unfortunately, an exaggerated emphasis on his prodigiousness rather than on his education, industry, and good fortune deprives his early biography of a number of its important lessons.
- Three of the proofs were published in Latin, the fourth in German.2 Thanks to the kindness of Ahmet Feyzioǧlu, who presented me with a recently published collection, “Cebirin Temel Teoremi için dört İspat”, of translations by Gülnihal Yücel, I had also the pleasure of reading the first proof, the one that concerns me here, as well as Gauss’s comments on the attempts of his predecessors in an elegant contemporary Turkish. The refusal of the vernacular not only by mathematicians in countries to which modern mathematics came late but also by those in countries like France, Germany, Russia in which it was once vigorous and in which the older, vernacular mathematical literature is still extremely important has cost mathematics and mathematicians more than they have gained and more than they imagine—even if it is just the leisure to reflect undisturbed on our own ideas. So it is a joy to see even modest efforts to counter it.
- I am very likely reading more into Descartes’s explanations than is present there. I have made no effort to discover what precisely he could have had in mind with the notion of degree of a curve when writing the supplement on geometry that is attached to the Discours. In some sense, but I suppose it has to be a very weak sense, he anticipates the theorem of Bézout, first formulated by the French mathematician Étienne Bézout in the eighteenth century. It affirms that the intersection of two plane curves defined respectively by an equation of degree m and one of degree n has in general mn points. Bézout was the author of textbooks on algebra used in French lycées of the period. He has also acquired an extremely modest extra-mathematical notoriety. The novelist Stendhal, who as Henri Beyle began his career as a student of mathematics, flaunts in his memoirs his knowledge—not substantial—of mathematics and, in particular, is given to mocking Bézout.
- Whether the effort was worthwhile is a fair question, especially for those concerned not with mathematics as such but the beauty of mathematics. Does mathematical beauty or pleasure require such an accumulation of concepts and detail? Does music? Does architecture? Does literature? The answer is certainly “no” in all cases. On the other hand, the answer to the question whether mathematical beauty or pleasure admits such an accumulation and whether the beauty achieved is then of a different nature is, in my view, “yes”. This response is open to dispute, as it would be for the other domains. My purpose here is to make the case for a mathematical beauty that transcends neither the simple mathematical pleasures of arithmetic and geometry nor the fascination of difficult problems but that integrates them with the quite different intellectual pleasure of creating order from seeming chaos, even in an inconsequential—but not for me—realm. One man’s order is sometimes another’s chaos. So I do not expect everyone to be persuaded. I myself am haunted by Rudyard Kipling’s familiar conundrum,
And each man hears as the twilight nears, to the beat of his dying heart,
The Devil drum on the darkened pane: “You did it, but was it Art?”
Footnotes
- Equation (1.1) is: X^n+a_{n-1}X^{n-1} + \cdot + a_1X + a_0 = 0 ↩
- All are available in German, online at http://www.archive.org/details/dieviergausssche00gausuoft
