Ken Ono, a Professor of Mathematics at Emory University, USA, is a number theorist well-known for his work on the theory of integer partitions and modular forms. His work, and life, has been profoundly influenced by Srinivasa Ramanujan. Ono is an Associate Producer of the movie The Man Who Knew Infinity. His autobiographical book My Search for Ramanujan: How I Learned to Count, co-authored with Amir Aczel, was released in 2016. In September 2016, the contributing editors of Bhāvanā interviewed Ono over e-mail.

From your earliest memories, was there anything that led you to believe that mathematics was fun, that it was doable? Or did you develop an interest only because of your father?
Ono: My father is a mathematician, and I think I was blessed with some talent. Perhaps it was simply the environment in which I was raised. We had a chalkboard in the kitchen, and some of my earliest memories are of the two of us solving math problems at the board. My father was delighted that I seemed to be born with some talent.

But I didn’t love mathematics. I didn’t think it was beautiful. As a second grader, when I was seven or eight years old, I simply enjoyed the fact that my parents took delight in my performance. However, this would soon change.
Did your dad’s reputation as a first rate mathematician become a difficult cross for you to bear at any point, either when you were in school, or later, as a graduate student?
Ono: Yes. I couldn’t escape the fact that my father had a lofty reputation. In college I was known as Ono’s son.
When I was a student at the University of Chicago, Professor Walter Bailey, a distinguished number theorist, even invited me to his home for dinner. He did this as a favour to my parents. Instead of finding a friendly mentor in Bailey, I was intimidated by the fact that I could not enroll in mathematics courses as an anonymous student—I had nowhere to hide. It was a huge loss for me. I never saw Bailey again. I avoided him on campus. Back then I thought like a child. Instead of making the most of the opportunity to learn from a world-leading mathematician like Bailey, I preferred to avoid him like the plague, as if my safety depended on avoiding him.
“I had nowhere to hide”
You were mentored by your dad as a young lad, and taught the essence of even, surprisingly, Fermat’s Little Theorem. That must have been thrilling. Were there other instances when you learned of theorems from him that were posed as riddles?

Ono: Yes, indeed. My father taught me the finiteness of Gauss’ class number this way. He taught me the inequalities which define reduced binary quadratic forms, which in turn imply the finiteness. I understood the importance of the shape of the fundamental domain of \mathrm{SL}(2, \mathbb{Z})( See Box 1) before I had even heard of a group!
Could you elaborate a bit: How did you come to understand the importance of the shape of the fundamental domain of \mathrm{SL}(2, \mathbb{Z}) before you had even heard of a group?
Ono: Reduced forms are defined by inequalities on their coefficients. If you then let y=1, you obtain a quadratic polynomial in x. Gauss’ constraints dictate that the unique root of these polynomials lies in the fundamental domain of \mathrm{SL}(2, \mathbb{Z}).
As a class, don’t binary quadratic forms include equations such as the Brahmagupta–Pell equation? Could you elaborate more on how you picked up these ideas at home?
Yes, the Brahmagupta–Pell equations offer beautiful examples of indefinite binary quadratic forms and the infinitude of their integer solutions. For example, the infinitude of the number of integer solutions to the equation x^2-2y^2=1. My father taught me about positive definite binary quadratic forms, expressions like x^2+y^2 and x^2+5xy+3y^2. Unlike the Brahmagupta–Pell forms, positive definite forms cannot represent a single number with infinitely many different integer points (x,y). Gauss proved that forms with common discriminant form a group, one which appears to be infinite at first glance. But it turns out that this group is finite once one recognizes that they lie in finitely many equivalence classes (think changing variables). The reduced forms are canonical representatives for these classes.
The concept of fundamental domain is perhaps best described, although a bit imprecisely to start with, by the following simple example.
To cover the flat floor in a large hall using regularly arranged tiles, we typically choose a particular shape for the tile, such as a square or a regular hexagon or any other shape, and systematically arrange them row-and-column-wise without any overlaps or leaving gaps between tiles. The size of the flat floor or the particular shape for the tiles chosen does not matter here; the hall could be as large as you want, extending indefinitely to what is mathematically called the Euclidean plane. This is expressed in technical terms by saying that a regularly repeated shape, or the basic tiling unit such as a square, is a fundamental domain for the Euclidean plane. That is, if there are an infinite number of square tiles of unit sides, then the Euclidean plane can be covered by placing them sideways in both row and column directions in integer units; technically expressed, these are rigid motions by integer units on the plane.
In modern terminology, Euclidean geometry is described by the standard notion of distance between any two points on the xy-coordinate plane. The Euclidean distance between two points (x_1,y_1) and (x_2,y_2) is the number \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}. A straight line in the coordinate plane is the set of points (x,y) satisfying the equation y=mx+c where m and c are fixed parameters. Similarly, x^2+y^2=a^2 gives the set of points on a circle with origin as centre and radius a. A rigid motion by integer units on the plane is represented by an ordered pair (m,n) of integers that moves a point (x,y) in the plane to the point (x+m,y+n); for instance, the pair (1,0) represents the rigid motion, called translation to the right, by unit 1.
The significance of straight lines in Euclidean geometry is that they are the shortest paths between two points. In other words, straight line paths realize the Euclidean distance between two points. Euclid’s description of geometry of the plane starting from five basic statements called postulates, the fifth of which is the famous parallel postulate, ignited the curiosity of generations of mathematicians. The parallel postulate states that given a straight line l in the plane and a point p, also in the plane but not lying on l, there is exactly one straight line through p in the plane that is parallel to l—that is, a straight line through p that never meets l even if extended indefinitely in either direction.
Trying to understand why the parallel postulate was necessary to describe the geometry of the Euclidean plane, mathematicians discovered geometries very different from that of Euclid after a long struggle of about 2000 years. One of these non-Euclidean geometries is hyperbolic geometry, in which there are infinitely many straight lines satisfying the parallel postulate.
A commonly used model to describe hyperbolic geometry is the upper half-plane, for which the underlying set is the set of points (x,y) in the xy-plane with y>0; and the hyperbolic distance between two points (x_1,y_1) and (x_2,y_2) in the upper half-plane is given by the formula \cosh^{-1}(1+((x_1-x_2)^2+(y_1-y_2)^2)/2y_1y_2). The upper half-plane endowed with this notion of hyperbolic distance is called the Hyperbolic plane.
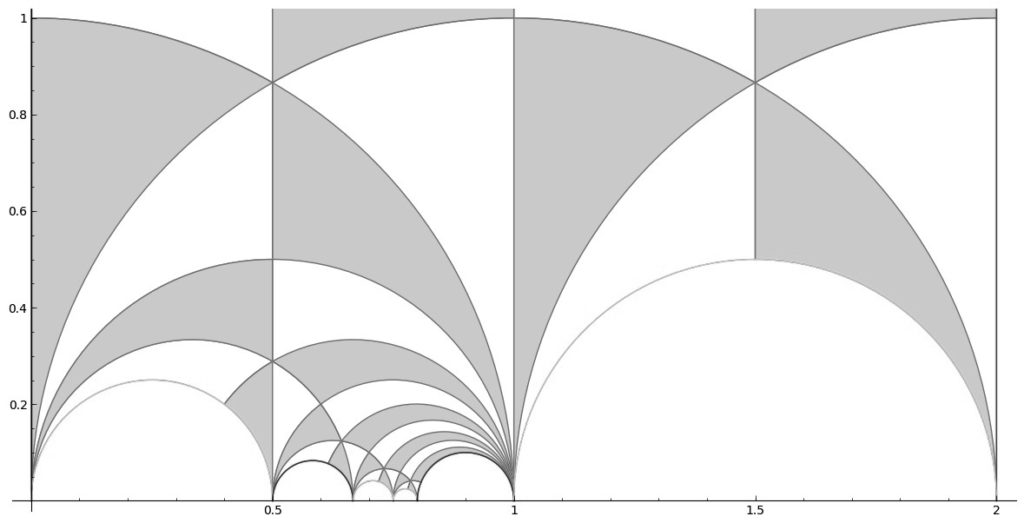
The analogues of the straight lines of Euclidean geometry (or the shortest paths between two points) in this model of hyperbolic geometry turn out to be circular arcs perpendicular to the x-axis (half-circles whose origin is on the x-axis) and straight vertical rays perpendicular to the x-axis.
The set of points on the upper half-plane are also described as the set of complex numbers z=x+iy with imaginary parts \Im z>0. Just as ordered pairs (m,n) \in \mathbb{Z}^2 represent certain rigid motions of the Euclidean plane, the set \mathrm{SL}(2, \mathbb{R}) of 2 \times 2 matrices \(\bigl(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \bigr)\), with a, b, c, d \in \mathbb{R}, ad - bc = 1, represent rigid motions of the Hyperbolic plane. This matrix moves a point z in the upper half-plane to the point (az+b)/(cz+d), which also lies on the upper half-plane, and preserves the hyperbolic distance between any two points in the upper half-plane. In particular, the elements of the set \mathrm{SL}(2, \mathbb{Z}), where a, b, c, d are integers, are rigid motions of the Hyperbolic plane.
Just as the square tiles fill the Euclidean plane, \mathrm{SL}(2, \mathbb{Z}) copies of any one-shaded shape in the above figure fill all of the Hyperbolic plane; in other words, it represents a fundamental domain for \mathrm{SL}(2, \mathbb{Z}). Some of the beautiful art works of the Dutch artist M.C. Escher, inspired by this model of hyperbolic geometry, serve to illustrate this concept graphically.
Who are the other people in your life whom you would consider your gurus, as we in India would reverentially address one’s mentors and teachers? What influence did they have at crucial junctures in your life?
Ono: I have many gurus. In college I had Paul Sally, the University of Chicago “Pirate Professor”. Sally took me under his wing when I needed help. I was a troubled student for the first three years of college. I was getting by with a 2.7 grade point average (C work). I was spending all of my time at parties and racing bicycles. I did my best to avoid my school work. Paul Sally rescued me before it was too late.
In 1988, I watched Letters from an Indian Clerk, a documentary about Ramanujan, a man I had not thought about for four years. I was mesmerized by the story again, and this time I was ready to accept the message. I applied myself in my last year of college with Sally’s help. He saw talent in me—others had given up on me—and he singlehandedly got me into top PhD programs.

In graduate school at the University of California, Los Angeles, Basil Gordon transformed me. He took me on long walks on the beach. He played Chopin nocturnes for me. He recited poetry to me. Before we did any mathematics, we spent months talking about culture. He told me that I first had to learn to see beauty in the world before I could do creative mathematics. Together, we read Robert Kanigel’s book, The Man Who Knew Infinity. Gordon suggested that I follow Ramanujan’s mathematics. Gordon was my guru.
British analytic number theorist Andrew Granville was like my Hardy. Granville groomed me right out of graduate school. My professional success has a lot to do with the lessons he taught me as a new PhD.
1984 was, we hear, an important year for you. A strange and unplanned event led to your first real contact with something very Indian. Tell us what happened.
Ono: On April 7, 1984, a mysterious letter arrived at my home in Baltimore, Maryland. The letter was from an 80-year-old widow. The letter thanked my father for making a gift which helped fund the commissioning of a bust which honoured the memory of her late husband, a man who died over 60 years earlier.
This letter brought my father to tears. Ordinarily a stoic man, I was struck by my father’s emotional response. It would take me almost 20 years before I understood the significance of the note from Janaki Ammal, the widow of the late Srinivasa Ramanujan. As a 16-year-old, I only understood that my father revered Ramanujan, a two-time college dropout who had somehow inspired mathematicians before his untimely death. My takeaway was one of hope. I learned that my father revered a man who had not earned perfect test scores and grades. Indeed, he held a college dropout in high esteem. I needed to know that it was possible to earn parental respect without being a perfect student. In Ramanujan I found hope for my own life.

Around 1997, when things seemed to have settled down both personally and professionally, a much awaited moment of catharsis involving you and your father had yet to happen. Could you elaborate on this event please?
In 1997, I finally learned why my father was brought to tears by the letter from Janaki Ammal 13 years earlier. I learned this at the Institute for Advanced Study, Princeton, where I was a Member.1 I reconnected my father with the great André Weil shortly before Weil’s death. They had not seen each other for nearly 20 years.
My father was discovered by Weil in 1955, at the Tokyo-Nikko Conference, which is most well-known for its role in the history of Fermat’s Last Theorem. The conference was held in the spirit of peace and reconciliation after the bloody world war. The United States hosted the conference as part of an effort to rebuild Japan. André Weil was one of the distinguished mathematicians who attended the meeting. The young Japanese students were ready; they were hungry, not just for knowledge but also for food. Japan at the time had food shortages.
Inspired by the young Japanese students, Weil delivered an impromptu lecture one evening. He wanted to inspire the young Japanese, for he himself had struggled early in his career—he had escaped as a prisoner of war, then endured being ignored by senior mathematicians who did not understand the value of his early work. That evening Weil told the starving Japanese about a mysterious Indian genius. He told them about Ramanujan. There is no wonder now that so many Japanese mathematicians have gone on to study mathematics inspired by Ramanujan. They learned about Ramanujan at the very meeting where they found their own hope. For my father, Ramanujan symbolized hope and represented his own discovery as a mathematician.
In 1992, you considered seppuku, taking your own life. In your book, you also talk about the mathematician Yutaka Taniyama who did take his life. Do you think academia is not open about the personal difficulties that researchers sometimes face?
Ono: Yes, we do not talk so much about mental illness and personal struggle. However, these problems are very common. Earning a PhD is hard. Proving theorems on subjects which have confounded others is hard. Struggling for months on a problem can be maddening. Combined with the very high expectations set for me by my parents, I ended up hearing voices. I still hear them. However, I have been able to manage them.

Mathematics is vast enough that one could easily spend a lifetime in its study without making any new contributions to it. How and when did you realize that you could become a creator of mathematical knowledge rather than just a consumer?
Ono: Basil Gordon taught me how to do mathematics. Of course I read papers and books. However, if you were to visit my home you wouldn’t find any books. I spend over half of my time working without the influence of research articles, books, or the internet. I spend a lot of time alone wondering, with pads of paper, about the unwritten properties of the objects I like studying.
“I spend a lot of time alone wondering, with pads of paper, about the unwritten properties of the objects I like studying”
What are the kinds of mathematical questions that appeal to you? Do you have a philosophical outlook that informs your mathematical tastes?
Ono: I like to work on problems which seem to have beautiful solutions. I am not very skilled with long and complicated proofs. Instead, I enjoy problems which turn out to have a beautiful and crystal clear solution.
Is there a particular mathematical work of yours that has given you a sense of pride?
Ono I am very fond of my work on Ramanujan’s partition congruences. I first learned about them on television, and I fell in love with them at first glance. I am very happy that I was able to add to the theory in my work.
You have worked on the Rogers–Ramanujan Identities, (See Box 2) which are continued fractions as well. Are these identities some kind of a bridge between physics and mathematics?
Ono: Yes. The Rogers-Ramanujan identities appear in many places in science: birth-death processes, statistical mechanics, algebraic geometry and, of course, number theory. In these identities we find pure inspiration, which in the final analysis—if I can be so bold—has inspired the theory of vertex operators, Moonshine, and now is being put to good use in string theory and the invariants related to black holes.
The Rogers–Ramanujan continued fraction is defined as
\[R(q) = \cfrac{q^{1/5}}{1 + \cfrac{q}{1 + \cfrac{q^2}{1 + \ddots}}},\]
where q can be a real or complex number. This fraction emerges in the study of hypergeometric series, which are a type of power series. It represents the ratio of two hypergeometric series that appear in the Rogers–Ramanujan Identities. G.H. Hardy, in one of his lectures on Ramanujan’s work, opined that Ramanujan’s investigations into hypergeometric series and continued fractions “suited him exactly, and here he was unquestionably one of the great masters”.
This continued fraction has seeped into diverse areas of science over the years. One recent example is borne out through the work of P.R. Parthasarathy and R.B. Lenin at the Indian Institute of Technology, Madras, along with W. Schoutens and W. Van Assche at the University of Leuven, Belgium, in 1998. They showed that the Rogers–Ramanujan continued fraction provides a convenient way of understanding the dynamics of queue formation.
Being in a queue is a ritual we all engage in daily. There are obvious physical queues like traffic on a road, and there are more subtle queues, such as when we search Google and wait a fraction of a second while their servers respond to millions of other search queries made before ours. In these cases, how much time will be spent in the queue, or how quickly the queue will grow with time, are some of the important questions addressed by queueing theory.
Many factors determine the dynamics of the length of a queue, two of which are the arrival rate and the service rate at the queue. These are the rates at which new members join and leave the queue, respectively. In a queueing model, one first chooses appropriate arrival and service rates, along with other parameters of the queueing system. Then, one typically calculates the probability that a queue which initially has m members in it will grow or shrink to n members after t units of time. This probability, denoted p_{mn}(t), emerges as the solution of a set of differential equations known as the Chapman-Kolmogorov equations.
Once this probability is calculated, many other quantities of interest about a queue can be easily found, such as the average time the i-th member of a queue will have to wait to be served. p_{mn}(t) is relatively easy to compute when the arrival and service rates are independent of queue length. Such models approximate the dynamics of some real world queues quite well, such as the queue of waiting phone calls at a call centre. However, in models where the arrival or service rates depend on queue length, computing this probability becomes a lot trickier and involves more sophisticated techniques.
Parthasarathy and collaborators discovered a queueing model that is intimately connected to the Rogers–Ramanujan continued fraction. This is a queue where \lambda_n + \mu_n = 1 and \lambda_{n-1} \mu_n = q^n, where 0 \leq q \leq 0.576148\ldots, with \lambda_n and \mu_n representing the arrival and service rates of the queue when it has n members in it. For this queue, it can be shown that \lambda_n increases with n and, consequently, \mu_n decreases with n. The authors refer to this queue as the “more-the-merrier” queue, where the probability that a new member joins it increases with the queue length, while that of a member leaving decreases with the queue length. Such behaviour can be seen, for example, when a crowd of onlookers quickly grows in size because each person feels there is something “interesting” taking place and joins the crowd, which makes it even more likely for another person to join, and less likely for someone to leave.
The authors showed that with such a process, the Laplace transform of p_{00}(t) \equiv p_0(t) defined as f_0(s) = \int_0^\infty p_0(t)e^{-st}dt, is \[f_0(s) = \cfrac{1}{s + 1 – \cfrac{q}{s + 1 – \cfrac{q^2}{s + 1 – \ddots}}},\] which is the Rogers–Ramanujan continued fraction when s=0. Here, p_0(t) is the probability that no one is in the queue after time t. The probability that n people are in the queue after time t can then be approximated by considering convergents of f_0(s).
In joint work with Zachary Kent and Amanda Folsom, you have connected partitions of a number, which is Ramanujan territory, with fractals, which the world started to take note of only after computer graphics became powerful enough to capture their rich geometric and topological complexity. And this was a connection that was not there at all before you arrived. Tell us more about this work.
Ono: Ramanujan’s partition congruences have informed me in many ways. I am certain that Ramanujan understood much more than the congruences he proved and conjectured. I think we simply worked out a picture that he already had in mind. Even when congruences do not exist, it turns out that there are self-similar patterns with increasing resolution, in analogy with fractal geometry. However, these properties are about congruences.
That is very intriguing. Could you elaborate more on how this idea of attacking the partition problem from a fractal point of view came about?
Ono: The idea was an accident. Zach and I went for a hike in the north Georgia mountains. On a walk to some waterfalls, we marvelled at the lovely colours of the leaves on the heavily wooded trail. I naively remarked that the partition numbers formed our mathematical forest, and it dawned on us that we should try to assemble a theorem which explained what a walk along the partition numbers would look like. When we formulated this question, we naturally found what we had been searching for. (See Box 3)
Ono’s Work on Partition CongruencesThe partition function p(n) of a natural number n gives the number of distinct ways in which n can be expressed as the sum of smaller positive integers. As n varies, p(n) also varies. When Ramanujan started looking at the mysteries underlying partitions, he uncovered unexpected relations that connected p(n) to the world of primes. He observed that no matter how large p(n) became with increasing n, the following relations, now known as Ramanujan’s partition congruences, always held:
\[\begin{alignat*}{2}
p(5n+4) & \equiv 0 \,(\mathrm{mod}\, 5),
p(7n+5) &\equiv 0 \,(\mathrm{mod}\, 7), \mathrm{and}\,
p(11n+6) &\equiv 0 \,(\mathrm{mod}\, 11).
\end{alignat*}\]
The key point here is the presence of the prime numbers 5, 7 and 11 in the relations above. Ramanujan initially offered no proof of the above statements. But he was urged and prodded on by Hardy to provide a proof of his conjectures on the Prime Number Theorem, which led to the duo inventing the circle method. This invention was seen as a tool meant to not just prove Ramanujan’s statement, but also help prise out the structure that lay hidden behind what Ramanujan believed were his divinely inspired mathematical insights into the allied question of the partitions of a number. This synthesis, the result of the confluence of Ramanujan’s famed intuition and Hardy’s insistence on rigour and proof, finally manifested in a clearly laid out logical framework, and was founded on ideas involving the so-called contour integral from complex analysis.
In the mid-eighteenth century, Euler had discovered a way to calculate p(n). But as n becomes large, this method becomes intractable. The circle method of Hardy and Ramanujan, however, could be used to reliably estimate partitions of numbers much larger than was possible using Euler’s method. In 1937, the German-American mathematician Hans Rademacher discovered a new formula that, while based on the ideas of Ramanujan and Hardy, was, in Ono’s words, “a crazy infinite sum of perfectly good integers”. The adjective “crazy” is apt because the formula, expressed as a series approximation, flies in the face of what is expected of the successive terms of a convergent series. Each successive term in a convergent series ought to take a function closer to its final value. But in the formula that Rademacher discovered, the successive terms fluctuate wildly, putting the very idea of convergence under a cloud. This fluctuation was an anomaly, and had to be either explained away, or justified and retained.

A fractal is a geometric object that is composed of many scaled copies of one basic shape, so that any locally observed part of the object is an exactly scaled replica of the original basic shape itself. Rademacher’s terms were hard to comprehend because they were not smooth, and had a lot of intrinsic jaggedness and fluctuations. Ono and Kent had found that the patterns in the physical forest surrounding them were suddenly mirrored in a completely different abstract space. A bridge connecting two faraway islands had been literally dreamt into existence.
This episode brings to mind what John Milnor, who was awarded the Fields Medal in 1962 and the Abel Prize in 2011, said he loves the most about the study of mathematics: its “anarchy”. “There is no mathematical czar,” Milnor said, “who tells us which direction we must work in, what we must be doing.”
The number 2719 makes an appearance in your research. It’s interesting to note that 2719 is a permutation of Ramanujan’s taxicab number, 1729. Tell us about 2719, and how it played a role in your own life as a mathematician.
Ono: I really like 2719. It turns out that it is related to an old paper by Ramanujan, on quadratic forms. Ramanujan asked for a rule which determines which odd numbers are not of the form x^2+y^2+10z^2, where x,y, z are integers. He raised this problem as an example of the general problem of determining which integers are represented by ternary quadratic forms. Kannan Soundararajan (Stanford) and I studied this problem, and we proved—subject to the Generalized Riemann Hypothesis—that 2719 is the largest odd integer which is not represented. I later found this number etched in charcoal in Sarangapani Temple, Ramanujan’s family temple in Kumbakonam. The sight of the number was thrilling. It seemed like Ramanujan was sending me a message.
While reviewing your Annals of Mathematics paper on the partition function in 2000, Bruce Berndt had these glowing words to say: “The theorems in the author’s paper represent the most exciting and significant work on congruences for the ordinary partition function since the inaugural conjectures of Ramanujan in 1919.”
Could you explain, in the simplest terms possible, why this work is seen as a landmark result, coming as it did nearly eight decades after Ramanujan’s original work?
Ono: Ramanujan’s congruences for the partition function only involved the primes 5, 7 and 11. My work involved every prime greater than or equal to 5.
Amir Aczel, with whom you wrote your book My Search for Ramanujan, was a prolific author of popular mathematics books. Sadly, he died last year, before your book could be published. What was the nature of your collaboration on this book? Was the book complete at the time of his death?
Ono: Amir was a good friend. I got to know Amir because of the articles and books he wrote on mathematics. In 2014, he wrote a story for Discover about my joint work on the Rogers-Ramanujan identities. He learned about my personal story, and wanted us to write a book. I didn’t agree at first, but over time I came to see the project as an opportunity to help young students who might benefit from hearing about my path.
The book was nearly finished when he died. Amir was a kind and loving man who did a wonderful job of sharing mathematics and science with the world through his writing.
Tell us about the Spirit of Ramanujan Math Talent Initiative. We read that you’ve already found a worthy young student to support through this initiative. How do you plan to nurture such talents through this programme? How would it accommodate talented people regardless of their age or qualifications?
Ono: The idea of Ramanujan is that talent is often found in the most unpromising of circumstances. This talent must be discovered and then nurtured. The Spirit of Ramanujan Global Mathematics Initiative is a search for talent in the world. Thanks to the support of the Templeton World Charity Foundation, we are offering fellowships and travel support for exceptionally talented undiscovered students. Details can be found here
Your students and mentees range from an athlete who at one time represented your country in the Olympics, to a professional songwriter who discovered a love for math when he was in his late thirties. Do you see kindred spirits in them when they come to you?
Ono: I have been blessed with an unusual collection of students. Perhaps mathematicians are naturally interesting people. I have never met a mathematician whom I did not find to be very interesting. I am drawn to students who have passion, and I am really interested in students who have multiple interests. I love all of my students. Having students is one of the best benefits one could ever ask for in any job.
What advice would you give to those who find themselves in the position you did decades ago struggling to meet expectations, both external and internal, and feeling lost?
Ono: Oh boy. I am not sure where to start! My first thought is that life is long. Have faith that you won’t be thinking about present problems a few years from now. At the end of the day, one should choose to follow a life path which does not lead to regret. Will you care about your grades from your death bed? Not a chance.
Choose to follow your passion. If you don’t have a passion, then find one. You only have one life, so live one which is true to yourself.
You have said in your book that “Searching for Ramanujan is my calling and it is my life’s purpose.” However, in another place in the book, you talk of the 2003 war in Iraq which triggered a spiritual awakening in you. While one is clearly mathematical, the other is difficult to define in precise terms. Can the two be reconciled, and if so, have you seen any common meeting points between them?
Ono: When I was young, I thought like a child. When I was in college, I still thought like a child. In fact, I thought like a child well into my 30s. I think that this is not uncommon. We live in an era where our young are taught to pursue and chase a life based on numbers—good grades, high test scores, highly ranked schools, high salaries, and so on. This isn’t living. Moreover, this mindless pursuit ignores the fact that we are all part of something much larger than ourselves. It takes time to reflect on our own individual roles, and I don’t see how one can do so properly without some sort of spirituality. In this regard, to each his or her own.
In mathematics, progress often involves flights of fancy. Just like Ramanujan gave credit to goddess Namagiri for his ideas, I believe that all great ideas are flashes of insight that are divine. Whether one believes that such flashes can be gifts from a goddess is not an important point to me. What is important is my strong belief that they are indeed divine, something heavenly.
“We live in an era where our young are taught to pursue a life based on numbers—good grades, high test scores, highly ranked schools, high salaries. This isn’t living”
Footnotes
- A visiting researcher at IAS, Princeton, is known as a Member. ↩
