Maryam Mirzakhani (1977–2017)

Maryam Mirzakhani, a great mathematician, passed away on 14 July 2017, at the age of 40. She is survived by her husband, her daughter, and her parents. She is mourned by those who knew her personally as a generous, brilliant colleague and friend, as well as by the much larger community of people who saw her as an inspiration.

In Memoriam

As a Muslim immigrant to the United States, and as a woman in mathematics, she had to overcome significant explicit and implicit bias. Her story, cut cruelly short, is truly remarkable.

Mirzakhani set standards that her peers aspired to achieve. Her PhD thesis, on hyperbolic geometry and dynamical systems, led to papers in the Annals of Mathematics [7], Inventiones Mathematicae [6], and the Journal of the American Mathematical Society [5], the top three journals in pure mathematics.

Mirzakhani, through deep study and hard work, developed deep and unusual insights into difficult subjects which she would share generously with colleagues. She was equally happy to have a conversation with a starting graduate student as with a senior faculty member. The impact of these discussions cannot be overstated. The confidence it instilled in people to have Mirzakhani take an interest in their work, and the particular creative ideas she would share, constitute a body of work whose influence is hard to assess by traditional measures like publications or citations.

Curves, Surfaces, and Spaces of Surfaces

Mirzakhani’s work is creative, deep, and innovative, centering on the geometry of curves on surfaces. An everyday example of a curve on a surface is the seam on a cricket ball, or even a line drawn on a piece of paper.

While a piece of paper is flat, a cricket ball, or its mathematical approximation, a sphere, is positively curved, meaning that it bulges outward at all points. There is a corresponding notion of negative curvature, where surfaces bulge inward. In a precise mathematical sense, most compact surfaces are negatively curved.

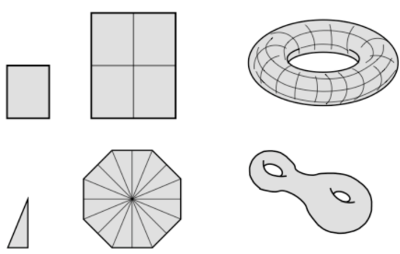
Compact surfaces are classified by their genus, or number of holes. A sphere has genus $0$ , the surface of a vada has genus $1$ , and two vadas fused together have genus $2$ . A round sphere has positive curvature; the surface of a vada, which can be constructed by gluing opposite sides of a piece of paper, has zero curvature; and any surface of genus $2$ or higher has negative curvature.

Spherical, flat, and hyperbolic soccer balls. The hyperbolic ball is always bending away from itself.

A concrete way of thinking about negative curvature starts with the tiling of the (flat) plane by regular hexagons. If you replace some of the hexagons by pentagons, you get the usual paneling of a soccer ball, that is, positive curvature. If, on the other hand, you replace some of the hexagons by septagons (seven-sided polygons), you get something that curves away from itself.

Curves on Surfaces

Mirzakhani studied the problem of counting simple closed curves on hyperbolic surfaces, which are surfaces of constant negative curvature (round spheres have constant positive curvature). Simple closed curves are ones that do not cross themselves, and are very rare amongst the set of all closed curves.

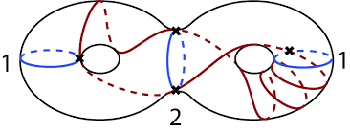
Simple closed curves—neither the blue nor the red curve intersect themselves

In precise terms, the number of closed curves of length at most $R$ grows exponentially in $R$ (in fact, like $e^R/R$ ). A typical closed curve of length $R$ has approximately $R^2$ self-intersections [4], whereas simple ones have none. Mary Rees [8] showed that there are upper and lower polynomial (like $R^{6g-6}$ , where $g$ is the number of holes, or genus, of the surface) bounds on the growth of the number of simple closed curves. Mirzakhani’s remarkable achievement [7] was to show that these bounds could be turned into precise asymptotic formulae. Moreover, averaging the coefficients of these polynomials over spaces of surfaces, yields inductive formulae in terms of averaged coefficients for simpler surfaces.

Spaces of Surfaces

Mirzakhani also interpreted these coefficients in terms of the size or volume of these spaces of surfaces, known as moduli spaces, and using these ideas, gave a new proof of the Witten conjectures, a deep result in mathematical physics.

On a personal note, I collaborated with Sasha Bufetov, Alex Eskin, and Mirzakhani [1] on a project to understand how volumes of balls in these spaces of surfaces grow, and to understand how to count multicurves, which are formal linear combinations of curves. This project was very important for my career, not just for the publication that resulted but rather for the ideas that I had the opportunity to exchange with my wonderful co-authors. Mirzakhani was always encouraging and positive, even when the technical difficulties looked overwhelming.

Billiards and Renormalization

Mirzakhani’s most recent work focused on mathematics that grows out of a simple model problem in Newtonian mechanics. Let $P$ be a Euclidean polygon, and consider the billiard dynamical system on $P$ —the motion of a point mass on $P$ with no friction, and elastic collisions with walls (that is, the angle of incidence $=$ angle of reflection).

The trajectories of this point mass are straight lines on $P$ with this rule of reflection on the boundary. If the polygon is rational (all the angles are rational multiples of $\pi$ ) we unfold the table to obtain a surface $S = S_P$ consisting of finitely many copies of $P$ with sides glued by translation, an object known as a translation surface. Billiard trajectories on $P$ become straight lines on $S_P$ . For example, if you start with billiards in a rectangle, the resulting surface is a torus obtained by identifying opposite sides of four copies of the rectangle, and if you start with a $\pi/8, 3\pi/8$ -right triangle, you obtain a regular octagon with opposite sides identified.

A fruitful technique for studying the long-term behavior of these straight-line trajectories is known as renormalization (though we are using this word somewhat differently than how physicists use it). To understand a long piece (say length $T$ ) of trajectory in direction $\theta$ , first rotate the surface $S$ until the direction is vertical—we call the new surface $r_{\theta} S$ , then contract the surface by $T$ in the vertical direction while expanding by $T$ in the horizontal, leading to a length $1$ piece of trajectory on a new surface, which we write as $g_t r_{\theta} S$ .

By understanding the shape of the new surface, we can recover information about the distribution of the trajectory on the original surface. Eskin and Mirzakhani, and Eskin-Mirzakhani-Mohammadi [2],[3], building on the work of many others, proved a remarkable result about this renormalization: the set of surfaces $M$ that can be approximated by renormalizations of a fixed surface $S$ can be described by linear equations in appropriate coordinates. More mathematically, the orbit closure of a surface under renormalization is an algebraic variety.

This result, described memorably by Anton Zorich as the ‘magic wand’ theorem, allows one to count special billiard trajectories, known as generalized diagonals, which are paths from corner to corner. As with much of Mirzakhani’s work, we are only starting to understand the impact of this theorem, which promises to yield many deep and beautiful consequences.

While Mirzakhani’s work will continue to have an enormous influence in several fields of mathematics, her loss will be felt deeply. On a personal note, I had looked forward to many more years of conversations about mathematics and other subjects, and exploring the directions in mathematics that she opened up. She will be missed as a colleague, a mentor, and a friend.

The 2014 Fields Medalists Artur Avila, Martin Hairer, Maryam Mirzakhani (with her daughter), and Manjul Bhargava at the ICM 2014, Seoul Gert-Martin Greuel/Archives of the Mathematisches Forschungsinstitut Oberwolfach

References

[1] J.S. Athreya, A. Bufetov, A. Eskin, and M. Mirzakhani. Lattice Point Asymptotics and Volume Growth on Teichmuller Space, Duke Mathematical Journal. 2012. 161(6): 1055–1111
[2] A. Eskin, M. Mirzakhani. Invariant and Stationary Measures for the SL(2,R) Action on Moduli Space. 2013. arXiv:1302.3320. 1–172
[3] A. Eskin, M. Mirzakhani, A. Mohammadi. Isolation, Equidistribution, and Orbit Closures for the SL(2,R) Action on Moduli Space. 2013. arXiv:1305.3015. 1–46
[4] S. Lalley. Self-Intersections of Closed Geodesics on a Negatively Curved Surface: Statistical Regularities. pp. 263–272 in: Convergence in Ergodic Theory and Probability (Columbus, Ohio, 1993), Ohio State Univ. Math. Res. Inst. Publ. 5. De Gruyter, Berlin, 1996
[5] M. Mirzakhani. Weil-Petersson Volumes and Intersection Theory on the Moduli Space of Curves. Journal of Amer. Math. Soc. 2007. 20(1): 1–23
[6] M. Mirzakhani. Simple Geodesics and Weil-Petersson Volumes of Moduli Spaces of Bordered Riemann Surfaces. Invent. Math. 2007. 167(1): 179–222
[7] M. Mirzakhani. Growth of the Number of Simple Closed Geodesics on Hyperbolic Surfaces. Annals of Mathematics. 2008. 168(1): 97–125
[8] M. Rees. An Alternative Approach to the Ergodic Theory of Measured Foliations on Surfaces. Ergodic Theory Dynamical Systems. 1981. 1(4):461–488

Jayadev S. Athreya, who collaborated with Mirzakhani, is at the Department of Mathematics, University of Washington, USA.