
Third edition, published 2020 by Chapman and Hall/CRC
346 pages
isbn 9781138061217
Close your eyes and imagine…
It is said that in some of his graduate classes in Princeton, the mathematician William Thurston (1946–2012) would say: “Close your eyes and imagine…”. The Shape of Space, a famous book, penned by one of his students, captures the reader’s imagination and draws her into the fascinating field of modern geometry.
This imagination or geometric intuition is arguably innate to all humans. Ever since the time we traversed the globe that we thought was flat, and marked out boundaries as we cultivated land, humans have been trying to “measure the Earth” and understand the shape of the world we live in. It is that grand question–-what is the shape of our universe?–-that the book leads towards, progressively uncovering some of the deep mathematical concepts and constructs that this age-old quest has generated.
Much like the bewildered Flatlanders in two-dimensional Flatsburg that the book opens with, we humans are at a point in history where we are baffled with observations of our own universe. Although astronomy has progressed by leaps and bounds since 2002, when the second edition of this book came out, which in turn has come an even longer way since the first edition in 1985, cosmological mysteries abound, like the preponderance of dark matter. The ideas in geometry and topology featured in this book are therefore quite relevant even today, and the publication of a fresh edition cannot be more timely.
Many of the mathematical notions discussed in the book had their genesis in the work of Carl Friedrich Gauss (1777–1855), and it is perhaps no surprise that Gauss himself had done field-work as a surveyor. One of his key insights was the Theorema Egregium, which established that a notion of curvature of a surface that quantified how much it bends in space was actually “intrinsic” to the surface. In other words, this Gaussian curvature could be calculated by a tiny ant who could measure the intrinsic metric on the surface (i.e. distances between points) but had no idea of the ambient space it was sitting in. To illustrate this, an ant on a “positively-curved” sphere will find that the area of a circular region is smaller than that of a disk of the same radius on a plane, whereas an ant on a saddle-shaped surface would derive the opposite conclusion.
It was Gauss who is also credited, along with Lobachevsky and Bolyai, with the first description of the “hyperbolic plane” where every point is intrinsically saddle-shaped, with the same negative Gaussian curvature everywhere. In this model of non-Euclidean geometry, the area of a disk grows exponentially with its radius, the sum of angles of a triangle add up to less than 180 degrees and there are a multitude of lines parallel to a given line L that passes through a given point not on L. This model also shows that the Parallel Axiom of Euclid was independent of the other axioms of Euclidean geometry.
This idea of using such “intrinsically defined” quantities to determine the shape of a space was vastly generalized by Bernhard Riemann (1826–1866), who was a student of Gauss. In his habilitation thesis in 1853, Riemann proposed a notion of an infinitesimal metric that could vary from point to point, and determined a notion of curvature that worked for higher-dimensional spaces as well. It was a deep insight that started a flurry of activity not too long after, that continues to this day. Indeed, in 1915, Einstein used Riemannian geometry to model our universe as a “curved space-time”, in an elegant theory of gravity that has proved to be stunningly accurate and immensely useful. Today, the GPS on our phones uses Einstein’s theory to correct for how the signals from the satellites are affected by the Earth’s gravity.
A few decades after Riemann, the work of Henri Poincaré (1854–1912) led to the birth of the subject of topology. In his attempt to solve a prize problem–-on whether our solar system is stable–-Poincaré realized that sometimes it is a qualitative feature of a space, like the number of “holes”, or genus, of a surface, that is relevant, instead of quantitative measurements of distances and areas that would be induced by a Riemannian metric. In particular, such topological features persist under a continuous deformation or “homotopy”. It was Poincaré who systematically defined various algebraic homotopy-invariants that generalized the notion of the “Euler number” of a surface. The Euler number is obtained by dividing a surface into polygonal regions, and calculating V- E+ F, where V is the number of vertices, E the number of edges and F the number of faces or regions.
These ideas from the 19th century now pervade mathematics, and there was a fascinating interplay between geometry and topology that unravelled over the next century. The two are inextricably linked in Thurston’s work on three-dimensional manifolds (or 3-manifolds in short), which this book eventually arrives at in its third part.
The first part of the book introduces topological spaces–-mostly surfaces (2-manifolds) and 3-manifolds, which lend to easy visualization, aided by the abundant illustrations that are all in colour in the new edition. Starting with basic vocabulary, it spends time on various constructions like cutting-and-gluing (quotients), adding handles and taking products, that help build more complicated manifolds from simpler ones. Indeed, any surface is obtained by adding handles to a sphere with “crosscaps” and a proof of this famous result, the “classification of surfaces”, is provided in the book’s Appendix. Part I includes a beautiful exposition of the topological notion of “orientability” where Escher’s ants on a Möbius strip, and tic-tac-toe on a Klein bottle make their appearance. It is this inventive and engaging nature of the book, with its various exercises, games (now available as smartphone apps), the occasional limerick, and even a dialogue (featuring Sagredo and Salviati, two characters in Galileo’s Dialogue Concerning the Two Chief World Systems) that makes it a unique experience for the reader.
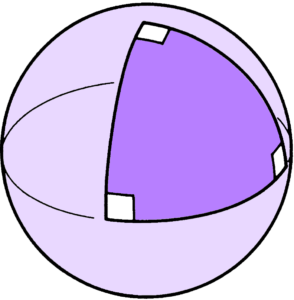
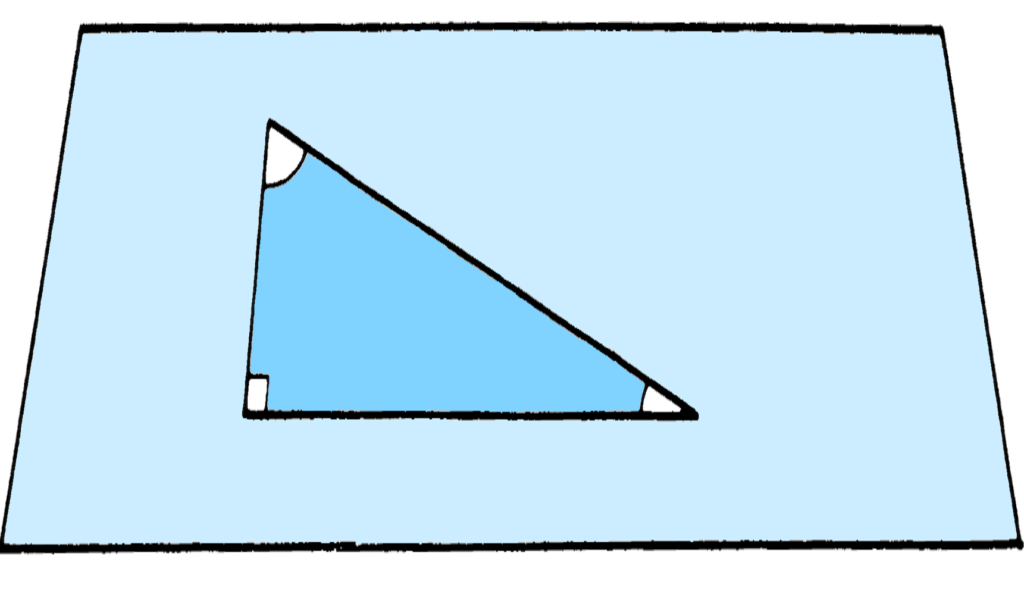
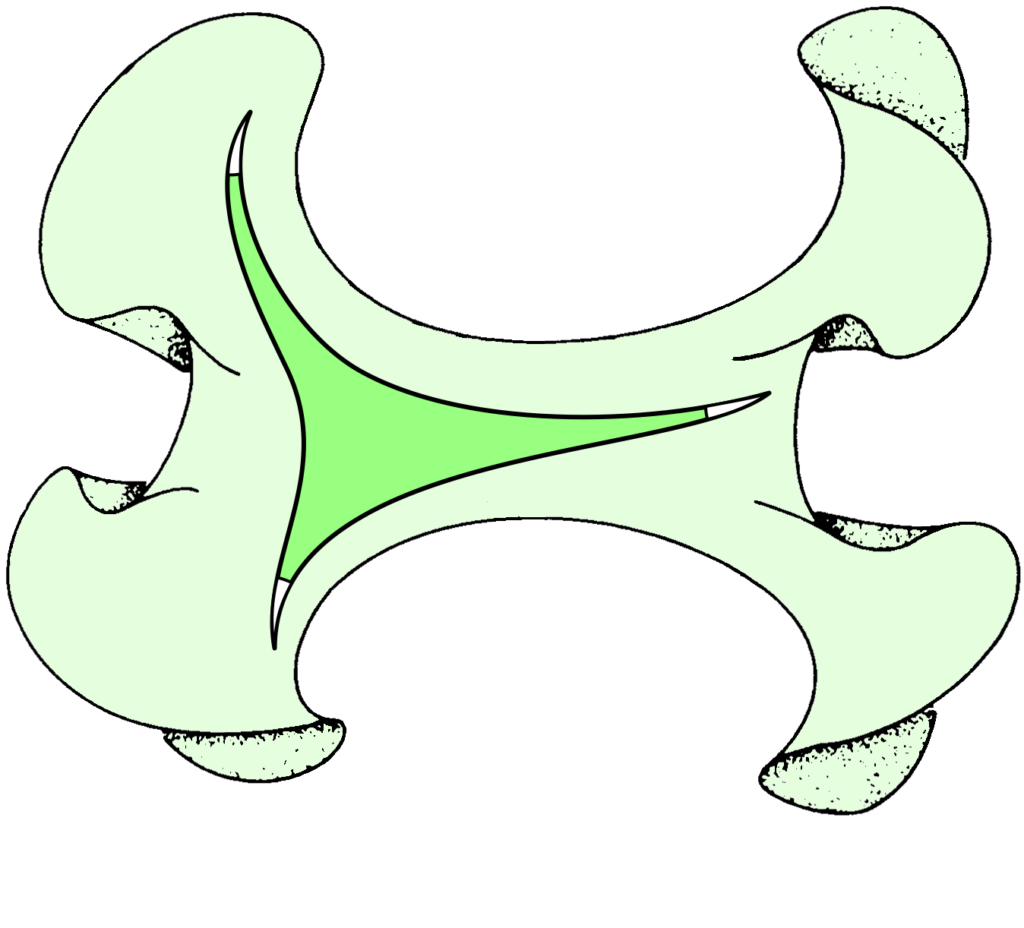
The three 2-dimensional homogeneous geometries Jeffrey Weeks
The second part of the book examines geometry in two dimensions, focusing on the non-Euclidean models of the round sphere \mathbb{S}^2 and hyperbolic plane \mathbb{H}^2, which are examples of “homogeneous spaces”. These are spaces which are isometric, i.e., look the same around any point. It turns out that any surface can be “geometrized”, that is, it can be given a geometry that locally looks like one of the three model spaces \mathbb{S}^2, \mathbb{H}^2 and the Euclidean plane \mathbb{E}^2. Indeed, just like a torus can be obtained by gluing sides of a square on \mathbb{E}^2 by translations that are isometries of the Euclidean metric, most surfaces can be built by gluing sides of polygons in \mathbb{H}^2 by hyperbolic isometries. Part II culminates in the famous Gauss–Bonnet formula that relates the Euler number to the integral of the Gaussian curvature over the surface. This is a striking equation, since it has a topological quantity on one side and a geometric one on the other–-historically, one of the first bridges between the two worlds. The book gives a beautiful illustrated proof of the formula for constant-curvature surfaces where it is shown that the area of a triangle on the sphere or hyperbolic plane is related to the sum of its interior angles, and the formula pops out if one divides the surface into triangles and adds up these areas.
The classification of 3-manifolds was a more daunting enterprise compared to surfaces. The Geometrization Conjecture of Thurston, formulated in the 1970s, asserted that any topological 3-manifold can be divided into building-blocks that can be equipped with one of eight homogeneous geometries. In the third part of the book, Weeks introduces these geometries and discusses how various 3-manifolds can be modelled on these spaces. Apart from the “constant-curvature” spaces, which are the 3-dimensional Euclidean space \mathbb{E}^3, the hypersphere \mathbb{S}^3, and hyperbolic space \mathbb{H}^3, these model geometries include product spaces \mathbb{S}^2 \times \mathbb{R} and \mathbb{H}^2 \times \mathbb{R}, and three more “twisted” products like the Solv geometry (the “real weirdo”, as the book describes it). The latest edition of the book has fascinating illustrations of what it looks like to be living inside some of these spaces, like the Seifert–Weber space (that is modelled on \mathbb{H}^3) or the Poincaré dodecahedral space (that is modelled on \mathbb{S}^3).
In fact, Thurston had conjectured that most 3-manifolds are hyperbolic (i.e., modelled on \mathbb{H}^3), and proved that to be true for most knot-complements. This was implemented as a computer program called SnapPea by Weeks, that, given a knot, describes such hyperbolic structures as gluings of hyperbolic tetrahedra. These were part of a collection of deep, insightful conjectures that appeared in an article by Thurston in the 1980s (titled “Three-dimensional manifolds, Kleinian groups and hyperbolic geometry”1) that had a profound influence on research in the subsequent decades. In the first decade of the current century, not long after the previous edition of this book was published, almost all of these conjectures were proved to be true. In particular, the Geometrization Conjecture was proved by Grigori Perelman in a celebrated series of three papers put up online in 2002–03, using techniques in geometric analysis that have their own long history. Interestingly, one consequence of the geometrization of 3-manifolds was an affirmative answer to a question of Poincaré about a certain topological characterization of the hypersphere. This long-standing problem in topology, known as the Poincaré conjecture, was thus finally settled by a deeper understanding of geometry, completing a circle of ideas that spanned more than a century.
Weeks’ book is a timeless classic, and will certainly be enjoyed by generations to come
The final part of the book enters into the exciting frontiers of cosmology, which is a promising playground for applying the various concepts in geometry and topology introduced in the previous sections. It includes a helpful summary of the basic questions (e.g. Is the universe finite? Does it have a boundary?) that we have been wondering about since antiquity, and the evolution of our knowledge about them. In the second edition of the book, two 21st-century projects have been described that aimed to figure out the topology of the universe. One went by the name of “cosmic crystallography”, where the idea was to analyze repeating patterns of clusters of galaxies when we observe them from the Earth. The other involved examining the Cosmic Microwave Background (CMB) radiation, which is a tantalizing glimpse into the early universe in the aftermath of the Big Bang. Once again, the hope was that the pattern of homogeneity and fluctuations in the CMB data could tell us how the curvature of space is distributed, providing hints about the shape of our universe. These projects seem to have not yielded definitive conclusions, and the current edition concludes by saying that the global topology and curvature of our universe remain a mystery. So, the scientific effort is still on towards resolving it, with the vital help of geometry that has, amazingly enough, progressed to realms far beyond the more mundane ambition of “measuring the Earth”.
Even within mathematics, geometry has had an extensive reach, touching many diverse areas. The notion of space had also come up in classical mechanics in the 19th century, where manifolds arise as configuration spaces or phase-spaces of physical systems, which has evolved into the flourishing area of symplectic geometry. Also inspired by equations of motion, the analysis of partial differential equations is today intimately tied with the geometric theory of integrability, where Lie groups (manifolds which are also groups) provide an instructive and important class of examples. Geometry connects with discrete groups in the more recent field of geometric group theory, which played a key role in settling one of the conjectures in Thurston’s list from the 1980s. Even number theory often uses algebraic geometry, that has systematically developed analogues of various notions of Riemannian geometry in more general settings (for example, for shapes described by integers and finite fields, instead of real numbers). It would be wonderful to have expository accounts of these, similar to this book, conveying the key ideas in these fields in a friendly and lucid manner.
After all, Thurston himself once wrote that “mathematical ideas are often hard to transplant from mind to mind”. A book such as this, which conveys key ideas in geometry and topology, as well as some of the excitement of mathematical discovery, is precious. Weeks’ book is a timeless classic, and will certainly be enjoyed by generations to come. \blacksquare
Footnotes
- William P. Thurston. 1982. “Three-dimensional manifolds, Kleinian groups and hyperbolic geometry.” Bull. Amer. Math. Soc. (N.S.) 6(3): 357–381. ↩
