
enrico castelnuovo was an Italian writer and is the father of the algebraic geometer Guido Castelnuovo. His short story titled “Teorema di Pitagora” (Theorem of Pythagoras) was originally published in Italian in 1886 in the collection Sorrisi e lagrime (Smiles and Tears) of short stories by Enrico. It has been translated here from Italian by C.S. Aravinda, and an earlier version of this translation had appeared in Samasyā, 1998, 4(1, 2, 3).


Born in Venice in 1865, Guido Castelnuovo was one of the early and celebrated algebraic geometers of the Italian school. His interest in geometry was kindled by Veronese, who taught him at the University of Padua. Castelnuovo graduated from there in 1886, and spent almost all of his academic career at various universities of Italy. He also worked in close collaboration with leading mathematicians of the day such as Corrado Segre, Luigi Cremona, Alexander von Brill and Max Noether.
Early in his career, Castelnuovo sent one of his papers to Corrado Segre, a leading geometer of the time. The carefully annotated and prompt response from Segre took him by pleasant surprise. When he expressed his gratitude, Segre is supposed to have replied: “It is a bad habit, even if widespread, to praise papers without reading them. On the contrary I have the habit of reading all the papers I receive and of sending my remarks to the authors: I do with others what I would like others to do with me.” It is widely believed that the Italian school of algebraic geometry came into prominence during the years 1887–1891 that Castelnuovo spent in Turin. He would discuss geometry of algebraic curves with his mentor and collaborator Segre during long walks under the arcades of Via Po in Turin.

Castelnuovo was an invited speaker at the International Congress of Mathematicians in Bologna in 1928 and, from the title of his talk, La geometria algebrica a la scuola italiana (Algebraic Geometry and the Italian School), one can infer his deep concern for both research and teaching. He influenced an entire generation of young Italian mathematicians. Conforming to his own philosophy of how mathematics should be taught, he usually divided his course into two parts—the first part being a general overview of mathematics while the second part was more focussed. “[T]he reason for the division,” he wrote, “is that on the one hand it is necessary to have general culture, on the other hand it is necessary to have deep knowledge of a particular field.”
Among his most prominent students who has had a lasting impact in shaping algebraic geometry as a major mathematics discipline in the twentieth century was Oscar Zariski. It is an interesting and a well known story narrated by Zariski himself as to how he was examined by Castelnuovo on various topics in mathematics, without his knowledge, during a three-hour walk around Rome, at the end of which he told Zariski that he was taking him as his student.
Castelnuovo’s interests later turned to probability theory and the theory of relativity—he even wrote a book titled Calcolo delle probabilità in 1919 on probability theory and a text on the theory of relativity in 1923. He also took an interest in the history of mathematics.
During 1911–14, Castelnuovo was the president of ‘Mathesis’, an association for teachers in mathematics founded in 1895–96 and made decisive contributions to drafting the high school mathematics syllabus in Italy. The following quote1 bears testimony to his remarkable vision:
In the end, no school is truly effective unless it is able to engage an average intelligence, unless it is able to form an educated democracy, which is the base of every modern nation. To study the means by which education can be spread even at the expense of some depth—this is the problem that we are all called to solve!
His emphatic words2 about school education remain relevant today:
Middle schools should not furnish their pupils with knowledge, so much as with the desire and the need for knowledge. They cannot seek to provide an encyclopaedic knowledge of everything, but can only offer a clear, although necessarily very limited, idea of the principal issues examined by the various branches of knowledge, and of some of the methods which have been employed in tackling them. They should not be afraid of sacrificing profundity for range of ideas. Of course, this kind of teaching will not be sufficient to provide middle school students with preparation specific to one or another of the faculties of the university. However, this is not the aim of middle schools. They serve simply to provide students with the aptitude to move on to more advanced studies.


In another place,3 he notes:
It is often preferable to proceed by successive approximations, where each step is evaluated in relation to actual facts, in order to separate true from false bit by bit, rather than to rely on impeccable logic sealed off from the exterior world. The way mathematics is taught in schools nowadays shuns, wrongly, that first approach and therefore gives up on the only way of thinking that is common to most people. The emphasis on demonstrating through logic what is already evident intuitively causes a double damage in that it undermines reasoning, which has a different function, and intuition, by not acknowledging its immense value. One can always say that intuition can lead to mistakes; maybe. But intuition also provides the principal, if not the only, path to the discovery of truth. Should we really give up the truth for fear of making mistakes? If we are willing to strip elementary geometry of a whole series of mental gymnastics which serve no purpose, we might be able, I think, to reach two goals which at first glance might seem incompatible. We will be able to raise the pedagogical value of mathematics and, at the same time, nurture several mental abilities, instead of sacrificing everything to just one. Simultaneously, we will make mathematics enjoyable and accessible to everyone, finally defeating the prejudice that the very elements of this subject are only suitable to a few select minds.
Guido Castelnuovo was instrumental in bringing the University of Rome to high repute, and quite fittingly the Department of Mathematics there now bears his name—the Institute of Mathematics Guido Castelnuovo (Istituto Matematico Guido Castelnuovo).
He was deeply influenced by the life and work of his father Enrico Castelnuovo who was a celebrated Italian writer. In the following story (translated into English) the father Enrico Castelnuovo graphically relates his ignominious tryst with the celebrated theorem of Pythagoras to the unexpected return of the spectre of that forgettable event several years later in his son’s notebook. Although the story by itself carries a delightful humour throughout, it reflects a typical sentiment of many who prefer to stay clear of pursuing anything to do with mathematics. All the same, it amusingly brings to the fore the message that mathematical creativity need not be a hereditary enterprise.
The Theorem of Pythagoras
“The theorem of Pythagoras,” said Professor Roveni, sounding somewhat sarcastic, reading from the slip of paper I had just then taken out with my trembling fingers from a box on his table. Then showing it to the commissioned government official next to him, he whispered something in his ears. Finally he handed over the slip of paper to me to see the question myself with my own eyes.
“Go to the board,” he uttered, gently rubbing his hands together.
A student who had just been through with this examination ordeal before me stepped out of the classroom silently after freeing himself with supreme effort and, as he opened the door, a streak of bright sunlight entered the room. It fell on the floor and up the wall and I felt a slight relief seeing my shadow on that.
The door closed and the room became dimly lit as before. I must say that it was rather suffocating on that day in August, with the blue canvas curtains meant to prevent light coming in through the glass windows appearing insufficient against the fiery rays of the sun even with the windows shut. Whatever light was coming in was falling only on the black board, enough to display my defeat prominently.
Noticing my hesitation the professor said, “Go to the board and draw the figure.”
Drawing the figure was the only thing I knew and I took a chalk and began drawing the figure with total concentration. I didn’t have to hurry. Because the longer I took to draw the figure lesser the time I would be left with for the oral explanation.
But the Professor wasn’t the one to be fooled by my tricks.
“Yes, do it fast, you are not going to draw the Madonna of Raphael.”
I had to finish the picture now.
“Label the points now, fast! You are not displaying your talent of good hand writing. Why did you erase that letter G?”
“It resembles the letter C that I have already written. I was going to put H instead.”
“What a profound thought!” continued Professor Roveni with his usual sarcasm. “But are you done now?”

“Yes, done.” I then said to myself, “What a pity!”
“Now why are you silent? Get on with the proof of the theorem.”
Here began my tragedy. The details had slipped away from my memory.
“In a triangle …” I started shakily.
“Yes, go on.”
I collected all my courage and finished saying all that I knew: “In a triangle… the square on the hypotenuse is equivalent to the sum of squares of the other two sides.”
“In any triangle?”
An encouraging voice from behind hinted, “no, no!”
“No sir,” said I.
“Now go over again correctly—in which triangle?”
“In a right-angled triangle,” the voice behind prompted again.
“In a right-angled triangle,” I promptly reproduced.
“Silence! Out there!” the professor thundered.
Looking at me he continued: “So, according to you, the square on the biggest side is equal to that on each of the smaller ones?”
Good heavens! This is absurd. Sudden inspiration struck me.
“No sir, to them both added together.”
“To their sum then, say so. And then you should say that it is equivalent to and not equal to. Fine, go ahead and prove now.”
Although the weather was tropical and warm, I was cold with sweat. I stood looking stupidly at the right-angled triangle, the square on the hypotenuse, the two smaller squares sticking to it and tossed the chalk from one hand to the other without opening my mouth at all, for it was indeed true that I didn’t have anything to say!
Now no one prompted me. There was pin-drop silence. The professor cast his grey eyes straight on me, displaying a malevolent joy. The government inspector was taking notes on a piece of paper. Then all of a sudden the respected gentleman cleared his throat and Professor Roveni said, in a most insinuating manner, “Then?”
I didn’t answer.
Instead of sending me out he continued his interrogation with the pleasure of a cat chasing a mouse.
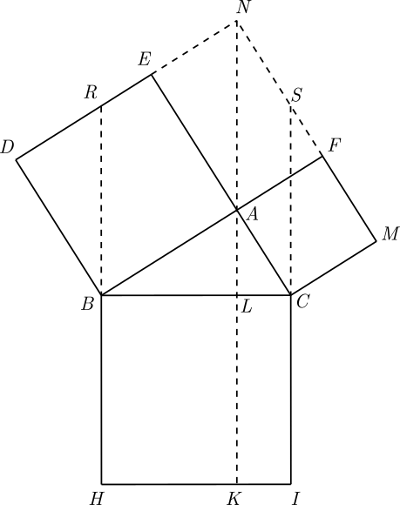
“Perhaps you are trying to find a new proof. I don’t say that you may not find one but we will be happy with any one of the well-known proofs. Go ahead, have you already forgotten to extend the lines DE and MF so as to meet at a point? Yes, do it now.”
I then mechanically extended the lines as indicated. Now my picture looked like a monster and I felt as if its heavy weight sat on my chest.
“Call the point where they meet N. Then what?”
I remained silent.
“Don’t you know that it is necessary to draw a straight line from N through A until it intersects the base of the square BHIC?”
Although I did exactly as he said I didn’t know any such thing.
“You should also now extend the two sides BH and IC.”
Uff! I couldn’t hold out any more!
“Now, even a two-year-old child can explain the proof,” the professor continued. “Do you have anything to say about the triangles BAC and NAF?”
Since the silence was killing, I said, “Nothing” briefly.
“That means you really know nothing?”
“You should have come to this conclusion earlier,” said I with a calmness that could have made even Socrates proud.
“Very right! Very right! Is that all you have to say? Don’t you even know that this theorem of Pythagoras is also known as Donkeys’ bridge because only donkeys cannot cross this bridge?… You may go now. I suppose you understand that you have not passed this examination. You should know the price you have to pay for reading Don Quixote or drawing pictures of cats during my lessons.”
The government official reached out for a pinch of snuff. And I left the duster and chalk on the table as I royally walked out of the room, noticing my classmates in suppressed laughters.
Three or four of them who had performed hardly any better than me in the same examination were waiting for me outside.
“Finished?” they asked eagerly.
“Finished indeed!” And putting up a brave face, said I, “Mathematics is only for the duds as I have always been saying.”
“Certainly so,” exclaimed one of my rivals.
“What did they ask you?” asked another.
“The theorem of Pythagoras. What do I care if the square on the hypotenuse is equal to the sum of squares of the other two sides or not?”
“It means nothing to you, to me, and to anyone in this world,” peevishly added a third in all the blissful ignorance of a fourteen-year-old. “Even if it is equal why should one keep on saying it time and again, and if not why should they trouble us about it?”
“Believe me my friends,” said I, continuing the discussion as if I were a lot more experienced. “It is absolutely true that this way of teaching is completely wrong, and it will not change as long as Germans are here in our country.”
Not only convincing ourselves that our failure was in protest against the Austrian domination, we went home firmly believing that it was an indication of our extraordinary intellectual maturity. But it was also true that all my initial enthusiasm in such matters vanished very soon without a trace.
Failing in this examination in such a shameful manner had a profound influence on my future. Since it was impossible for me to understand mathematics, the same day it was decided that I should leave studies and that I earn a living soon enough in view of the financial situation at home.
That was a very reasonable decision and I had no right to oppose it. However, I felt extremely sad. I had not the same hatred for other subjects as for mathematics and I had done quite well in these other subjects. Also I loved going to the school very much. Those sacred classrooms that would come alive with all our noises and those benches with our names engraved on them were all very dear to me. I was even very fond of the same blackboard which had witnessed my irreparable defeat.
I blamed the theorem of Pythagoras as the real culprit for all this. If it were some other question, who knows? I would probably have saved myself by a whisker as was the case in the previous years! But it was reality that it had to be this one.
It came in my dreams that night. It stood there right in front of my eyes—that terrible square with a triangle sitting on its head and the two smaller squares one leaning to its left and the other to its right. I saw the lines crossing each other and the confusion of the letters, as also the constant hammering on my head: BAC = NAF; RNAB = DEAB.
It took me a while before I could free myself from the stronghold of Pythagoras and his three squares and the nightmares. In the long run, however, time the great healer, which erases so many things, had also completely erased this from my memory until a few weeks back when the spectre of that image re-appeared in one of the notebooks of my son.
“Has this curse been passed on to my descendants too,” I exclaimed in horror. “Poor boy! What if the same theorem of Pythagoras proves fatal to my son as well?”
I decided to ask him about this as soon as he returned from school.
“Have you already come to the theorem of Pythagoras in geometry?” I began gravely.
“Yes, father,” he answered me with ease.
“Difficult proposition,” I said moving my head with hesitation.
“Do you think so?” he asked smilingly.
“Oh! Are you trying to boast and make me believe that it is easy for you?”
“I do find it really easy.”
“Then I must see you do this”—the words fell out of my mouth without my knowledge. “I don’t tolerate such boasting.”
“Yes, right away,” he said with juvenile confidence. And started off even before I was through with my sentence. Taking a piece of paper and pencil he quickly drew that devilish figure.
“There are many ways of showing this. I suppose it is alright if I follow any one of them?” he paused.
“Yes,” said I mechanically. It had to be alright as far as I was concerned. Even if there were a hundred different proofs I wouldn’t have been able to comprehend any one of them.
“Then let us take the one commonly used,” my mathematician son continued.
Extending the same lines which, twenty-seven years ago, unforgettable Professor Roveni had asked me to do, my son set out with supreme conviction to show that the triangle BAC is congruent to the triangle NAF, that the rhombus RNAB like a slave shared with the square DEAB and that so many other things were equal to each other, so that it came from a natural consequence that the BHIC square was equivalent to the sum of the two squares CAFM and DEAB.
Having finished with the proof my son said, “Now, if you wish, we can come to the same conclusion in a different way.”
“Since we have reached the end, let us rest for a while,” said I, a bit haltingly.
“But I am not at all tired.”

Not at all tired! Does it mean he is a junior Newton? But why do people talk of inheritance!
“You appear to be the first in your class,” I then said, in a voice not without a certain reverential fear.
“No, no. There are two of them who are better than I. Besides, as you very well know all except absolute donkeys understand the theorem of Pythagoras,” he added.
Excepting absolute donkeys! I was now hearing from my own son the same unforgettable words that Professor Roveni had used on that tragic examination day twenty-seven years back! In addition, the same words were ironically now prefixed by as you very well know.
I had to save my honour anyway and so I hastened to add: “Of course, I know it. I was saying it just for fun. But you are not going to be a fool to take pride in such a small thing.”
My Newton was now regretting the arrogant statement he had made. With a bit of embarrassment he said, “Even then some do not pay any attention to their lessons and studies. As a result… although they are not donkeys… I bet…”
As I felt that he was showing me a way of escape, at that instant, I said in all honesty, “That must be true. I suppose I didn’t pay much attention.”
“How come?… You?’, the boy burst out blushing to the root of his hair. Yet I bet at the bottom of his heart, he had a great desire to laugh.
I put my hand on his mouth, and said “Shh! Let us not start scratching for details in this matter.”
Thus, as one can see, the theorem of Pythagoras again put me in deep humiliation. However, I have no lasting resentment for it. True, any trust of friendship can never develop between us. Despite this, I convinced myself to consider it as a good family friend to whom it is not proper to be rude, nor is he personally disliked.
Footnotes
- G. Castelnuovo. 1909. Sui lavori della Commissione Internazionale pel Congresso of Cambridge. Relation del Prof. G. Castelnuovo della R. Università di Roma, Atti II Congresso della Mathesis, Padova. ↩
- G. Castelnuovo. 1910. La scuola media e le attitudini che essa deve svegliare nei giovani. Federazione Nazionale Insegnanti Medi. 33–47. ↩
- G. Castelnuovo. 1907. Il valore didattico della matematica e della fisica. Rivista di Scienza. 1: 329–337. ↩
