
The 2024 Infosys Science Foundation Prize in Mathematical Sciences category is the latest in a series of accolades that Neena Gupta of the Indian Statistical Institute (ISI), Kolkata has received for her significant work in mathematics. Introducing the awardee and her work, the following prize citation1 was read out by the Jury Chair Chandrashekhar Khare:
The Infosys Prize follows another signal recognition Neena received in the same year, on 21 February 2024, that of her being named the 2025 AWM-AMS Emmy Noether Lecturer. As a tribute to the great Emmy Noether2 (1882–1935), who has shaped our modern abstract algebraic thinking, the annual `Emmy Noether Lecture’ series was established in 1980 by the Association for Women in Mathematics (AWM) to honour women “who have made fundamental and sustained contributions to the mathematical sciences”. From 2015, this series is being jointly sponsored by AWM and the American Mathematical Society (AMS). These one-hour expository lectures are presented at the Joint Mathematics Meetings of AWM and AMS each January.
It is a matter of pride for the Indian mathematical community that Neena Gupta of ISI Kolkata, is invited to deliver the 44th Emmy Noether Lecture on January 9, 2025. She is the youngest mathematician so far, and is also the first from an Indian institution and the third of Indian origin to be chosen for this honour. Bhama Srinivasan from the University of Illinois at Chicago and Raman Parimala from Emory University at Georgia have earlier delivered the Emmy Noether Lectures in 1990 and 2013 respectively.

During 2021–2023, as India was celebrating 75 years of Independence, Neena had been receiving several other international and national recognitions. Apart from the Ramanujan Prize, Neena was an invited speaker at the International Congress of Mathematicians (ICM) organised by the IMU in July 2022 in two sections: (a) Algebra and (b) Algebraic and Complex Geometry. Such an invitation signals an entry into the “hall of fame for mathematics”.
The Honourable President of India conferred on Neena the `Nari Shakti Puraskar’ on 8 March 2022. A brief biography of Neena appears in the book Vigyan Vidushi, brought out by Vigyan Prasar, an autonomous organization under the DST, on the occasion of 75 years of Indian independence. The book was released on 28 February 2023 during the National Science Day programme of the Ministry of Science and Technology at Vigyan Bhavan, New Delhi.

During the previous decade, Neena had received all the major national scientific awards covering mathematics. In 2019, she earned the distinction of being the youngest ever mathematician to be awarded the nation’s then highest scientific honour, the Shanti Swarup Bhatnagar Prize. Earlier, the Indian National Science Academy (INSA) had described Neena’s work on the Zariski Cancellation Problem as “one of the best works in algebraic geometry in recent years done anywhere”, while awarding her their Young Scientists Medal (2014).
Neena’s research contributions have all been accomplished entirely in India. Apart from the citations in numerous awards, the importance given to her work by mathematicians in her area can be glimpsed from the recent book Polynomial Automorphisms and the Jacobian Conjecture by Arno van den Essen, Shigeru Kuroda and Anthony J. Crachiola, three leading experts in the field. This book, published by Birkhäuser in 2021, is on new results in affine algebraic geometry from the beginning of the present century. Chapter 3 of the book presents Neena’s first contribution on the Zariski Cancellation Problem in textbook style, developing all the concepts, tools and previous results needed to comprehend her work.
As many readers would be curious to know how Neena grew up to become a strong mathematician, I am sharing below a brief account of her early education and her initial research career till she became a faculty member at ISI Kolkata in 2014.
Neena’s Early Life and Education
Neena was born on 24 November 1984 at Alambazar in Baranagar, a place near the Dakshineswar Temple, Kolkata. She belongs to the Marwari community with roots in the Jhunjhunu district of Rajasthan. Her father Satya Narayan Gupta has been in service in Kolkata. Neena grew up in a modest middle class setup in Kolkata with her two brothers Rohit and Amit. She fondly recalls her father playfully setting mathematics riddles to his children; her mother Gyanlata too taught them till Class 10.
Neena studied from Nursery to Class 12 in Khalsa Model Senior Secondary School, near her home. Mathematics was her favourite subject in school. After completing Class 12 in 2003, Neena studied BSc Mathematics Honours at Bethune College, a historic women’s college affiliated to Calcutta University (CU). She had excellent performances in the college and university examinations, for which she won numerous medals and prizes in the form of books from her college.

Towards the end of her BSc studies, Neena came to know of the new MMath (Master of Mathematics) programme at ISI Kolkata and applied for it. The MMath curriculum had been initially designed as a continuation of an ambitious BMath programme that ISI had launched at its Bangalore centre from the year 2000. During the initial years, the MMath programme was too tough for most students entering after a standard BSc Mathematics course from a college, and very few students would be selected for it. Fortunately, beginning 2009, the course structure was revised to include a few basic topics in the initial semesters and that made the MMath programme more accessible to non-BMath students.
Neena joined the MMath programme at ISI Kolkata much earlier, in 2006, after getting selected through the stiff all-India admission test. Though Neena had good dedicated teachers at Bethune College, the CU BSc curriculum in her time excluded several core topics in mathematics, especially in abstract algebra. This made the ambitious MMath programme tough for her at the beginning and she says that initially she had feared that she would fail the course. But through her mathematical intellect, determination and hard work, Neena soon attained a strong mastery over all the diverse MMath subjects and received the Gold Medal for the best performance in her batch. Paradoxically, it is in algebra, the subject in which she was most under-prepared initially, that Neena began to best manifest her exceptional mathematical talent and originality. In an interview later, Neena identifies her admission to the MMath programme as the definitive turning point in her becoming a mathematician.
I taught her MMath batch courses in Algebra, Commutative Algebra and Algebraic Geometry and have been a witness to the swiftness with which she assimilated the course requirements in a short time. During her second year, she even attended some of our expository research seminars in algebra during vacations or when she did not have classes. She followed the seminar lectures and participated actively.
Neena acknowledges the conducive ISI environment for her success, especially the generous guidance she had received from the MMath teachers and the helpful discussions with some of her better-equipped batchmates. She is especially grateful for the help from her batchmate Arindam Banerjee who is now a faculty member in the Mathematics department of IIT Kharagpur. Arindam had joined MMath after completing the BStat programme of ISI where he had acquired considerable mathematical maturity. He was thus familiar with the system and comfortable with the course structure.
I feel tempted to narrate an anecdote here about Neena’s zest and motivation during the period. During the MMath admission interview, Neena had impressed all my colleagues in the interview board by her firm grip on the concepts she knew. As I mentioned, the MMath programme at that time assumed considerable prior knowledge of certain topics which were covered in the BMath programme but not in CU colleges – Neena too had not studied them. Towards the end of the interview, I advised her to study one such topic (basic ring theory) from the book Abstract Algebra by D.S. Dummit and R.M. Foote and mentioned a bookshop near our institute where the book would be available. The very next day, a senior member of our interview board found Neena at the bookshop purchasing the book!

In 2008, Neena got selected for the PhD programme at TIFR, for the Shyama Prasad Mukherjee Fellowship (SPMF) of the CSIR; and for the Special Research Fellowship of ISI for an outstanding PhD student. She decided to join ISI Kolkata for her PhD and opted for the SPMF. Number Theory and Algebra had become Neena’s most favourite subjects during MMath. There being no professional number-theorist in ISI Kolkata at that time, Neena registered for PhD under my supervision to work in Commutative Algebra and Affine Algebraic Geometry. She submitted her PhD thesis in September 2011 and obtained her PhD degree in February 2012.
Apart from accomplishing an impressive thesis, she undertook a study of numerous papers, old and new, on apparently diverse topics, which laid the foundation for her future glorious achievements. During the period, she had fruitful interactions with my PhD supervisor S.M. Bhatwadekar of TIFR and other renowned mathematicians like R.V. Gurjar and Ravi A. Rao of TIFR, T. Asanuma, N. Onoda and S. Kuroda from Japan, D. Wright from USA, and many others who had visited ISI; Neena also made a few visits to TIFR.
Neena as a budding mathematician
According to the Indian mathematician Mahāvīrācārya who lived in the ninth century, a mathematician can be recognized by the following eight qualities that he/she is endowed with:
- the ability to simplify and to express concisely;
- the ability to deduce valid results;
- the ability to disprove invalid statements;
- vigour in work and progress;
- the power of comprehension;
- the power of retention;
- the ability to find solutions of problems;
- the ability to discover mathematical facts through investigations.
Even after more than a thousand years, this can provide a beacon for a student enthusiastic about mathematics. Often we come across talented students of mathematics not realising their full potential due to a shortfall in just one or two of the listed attributes.

I share an anecdote in this regard. After teaching `Integral Extensions’ in the `Commutative Algebra’ course, I had listed some results on `integral closure’ from advanced commutative algebra, without proof or much discussions, to give an idea regarding the results known in higher dimensions. A few years later, while interacting with a renowned TIFR mathematician, she invoked one such (out-of-syllabus) difficult result that I had merely stated towards the end of a class at the end of a topic. It so happened that the senior mathematician was not aware of that particular result and thought Neena was making a mistake. But Neena confidently asserted that that was the statement I had stated in class. I was contacted, and I gave the precise reference and they could fruitfully make use of the result.
Indeed, apart from mathematics, she would remember each and every spontaneous word of advice or remark or idea – including those which I myself might have forgotten. I narrate one such anecdote which Neena recalled during her interview on Doordarshan after she won the Ramanujan Prize. During the initial days when she began studying research papers by stalwarts in her area and was overawed by the richness of magnificent ideas and techniques in their landmark papers, she had asked me how could someone like her solve any significant problem which eluded the giants in her area! She had no inkling then that, within a few years, she herself would be counted as belonging to that league of the stalwarts! I had told her that each person is unique and has a unique way of thinking and it is possible that her knowledge, strength and style could work for a particular problem, though the approaches of her brilliant predecessors didn’t. That is precisely what would happen in the case of the `Zariski Cancellation Problem’! I was pleasantly surprised to hear Neena narrate the anecdote on Doordarshan. While I have only a vague memory of the exchanges, Neena remembers the precise details.
So far, we have highlighted Mahāvīrācārya’s criteria (iv), (v) and (vi). We now consider (i) and (ii). From the outset, Neena has shown a flair for discovering short, neat and elegant algebraic proofs; however, when the research so demands, she has demonstrated the perseverance to toil through excruciatingly tedious investigations too.
Even during my MMath classes, Neena would correctly anticipate an approach or an argument on several occasions (for instance, the proof of “irreducible implies primary” when I was doing the theory of `primary decomposition’), a consequence of her rapid assimilation and internalization of algebraic ideas she comes across.

We now consider the point (iii) in Mahāvīrācārya’s list. In my MMath classes I had tried to inculcate among students a craftsmanship for constructing `counterexamples’ – examples which conclusively disprove an invalid statement. Neena responded admirably by constructing remarkable counterexamples to the True/False type questions in my Exercises.
Let me share an anecdote here. During his visit to ISI Kolkata in December 2002 and discussions with us, the eminent mathematician Shreeram Abhyankar, had been wondering whether a certain result on `associated primes’ extends to `non-Noetherian rings’. After considerable thought, I constructed a counterexample and felt thrilled about it; Abhyankar liked it. Later I used to ask the MMath students a modified version of the original query of Abhyankar. Neena and Arindam were the two students who independently came up with the counter-example, the same as my original example! That was one of the most fulfilling moments of my life as a teacher. A striking feature of the massive body of work of Neena, right from her PhD, has been the construction of fascinating examples illustrating unexpected twists.
During her PhD days, Neena had rediscovered a famous example of David Mumford (the Fields Medalist) of a “two-dimensional factorial ring which is not regular”, without knowing about Mumford’s work. It so happened that Mumford’s example was referred to by several speakers (including me) at the 2010 CAAG conference at IISc. When I made a passing mention in my talk that Neena had rediscovered the example by herself, algebraists in the audience were pleasantly surprised.
Another anecdote of February 2014, during the post-doctoral phase of her career. In an international conference at KSOM (Kerala School of Mathematics), there was a talk on a recent work of one of the leading figures in affine algebraic geometry and his junior collaborators but Neena felt uncomfortable with a main theorem presented in the talk. She kept thinking about it and by the time the next talk was over, she came up with a counterexample to the claimed theorem. The authors of the paper were taken aback. After discussions over the next few days, they modified their original hypotheses to address the lacuna revealed by Neena’s example, and presented a corrected version of their result at the end of the conference.
Before discussing items (vii) and (viii) in Mahāvīrācārya’s list and recalling her grand achievements around the `Zariski Cancellation Problem’ immediately after her PhD, we give brief introductions about Zariski, the research area `Affine Algebraic Geometry’ and the cancellation problem.
On Oscar Zariski (1899–1986)
Oscar Zariski played an important role in laying the foundations of modern Algebraic Geometry. As the name suggests, the subject treats geometry algebraically as in High-School `Coordinate Geometry’ where geometric problems involving straight lines and conic sections are transferred to algebraic problems involving solutions of linear and quadratic polynomial equations in one or two variables. This Coordinate Geometry was developed mainly by Rene Descartes (1596–1650) in the seventeenth century. Much more advanced and sophisticated results in geometry were obtained subsequently, especially by the Italian algebraic geometers of the nineteenth and early twentieth century. But the later progress of the subject came at a price. The algebraic geometers of the Italian school were unable to develop a sufficiently precise axiomatic foundation of the subject. Consequently they had to write about their interesting results in an informal style; their methods lacked the rigour of modern mathematics.

Apart from contributing deep theorems in both commutative algebra and algebraic geometry, Zariski was also the mentor of several big names of twentieth century algebra and algebraic geometry. His PhD students include Shreeram Abhyankar, Heisuke Hironaka, David Mumford, Daniel Gorenstein, Irvin Cohen, Abraham Seidenberg, Pierre Samuel, Michael Artin, Robin Hartshorne, Steven Kleiman and many other important mathematicians.
Oscar Zariski was born in the city of Kobryn, then a part of the Russian Empire. His original Russian name was Ascher Zaritsky. He pursued his initial mathematical career in Italy where he westernized his name. He obtained his doctorate from the University of Rome under Guido Castelnuovo (1865–1952), a leading algebraic geometer of the Italian School. Zariski eventually settled in Harvard University, making it a world centre for algebraic geometry.
The Indian mathematical community is indirectly indebted to Zariski for his contributions to algebraic geometry and commutative algebra, two of the subjects in which Indian mathematicians have made a mark in world mathematics.
Affine Algebraic Geometry
Affine algebraic geometry is a branch of algebraic geometry intimately connected to commutative algebra. Roughly speaking, affine algebraic geometry focuses on properties of what are called `affine spaces’ over a `field’ or over a `ring’. A `field’ can be thought of as a collection (like the collection of real numbers \mathbb{R}, the collection of complex numbers \mathbb{C}, the collection of rational numbers \mathbb{Q}) where one can perform addition, subtraction, multiplication, and division (except by 0). On the other hand, a `ring’ is a collection (like the set of integers) where one can always perform addition, subtraction and multiplication but not necessarily division. Polynomials in n coordinates over a field k form a ring called, polynomial ring; for instance, all polynomials in X and Y form a polynomial ring denoted by k[X,Y]. For any polynomial f(X,Y), the set of polynomials (in X and Y) modulo f(X,Y) also forms a ring denoted by k[X,Y]/(f).
Certain fields contain a relation of the form 1+1+ \cdots +1=0; they are said to be of `positive characteristic’; otherwise a field K is said to be of `zero characteristic’. An example of a field of positive characteristic is the binary set \{0,1\} with usual addition etc, except that 1+1 is defined to be 0. The structure of this field with two elements is precisely the mathematical principle (binary arithmetic) for the computer. The field of real numbers, the field of complex numbers, the field of rational numbers, are all of zero characteristic.
An affine n-space over a `field’ K is simply K^n, the collection of all n-tuples of elements coming from the `field’ K. The collection is given some additional structures called `Zariski topology’, `sheaf of regular functions’, etc. An example of an affine space is {\mathbb{C}}^2, the collection of all pairs of complex numbers.



The `Abhyankar–Sathaye Conjecture’ (named after Abhyankar and his student Avinash Sathaye) surmises that the Epimorphism Theorem extends to higher dimensions as well. In general it is often very difficult to determine whether a certain polynomial is a coordinate in a polynomial ring. Therefore, results like the Epimorphism Theorem, or affirmative solutions to the Abhyankar–Sathaye Conjecture, even in special cases, are of enormous value for algebraists and geometers.
The most fundamental and challenging problems on affine spaces include the `Embedding (or Epimorphism) Problem’ (which includes the Abhyankar–Sathaye Conjecture) and the `Zariski Cancellation Problem’. G. Freudenburg had remarked in the first edition (2006) of his Springer book Algebraic Theory of Locally Nilpotent Derivations (p. 235):
The `Jacobian Problem’, the most famous problem on affine spaces, is included by Fields Medalist S. Smale as the 16th among 18 problems for the 21st century. A nice discussion on these problems is made in the article Challenging problems on affine n-space by H. Kraft.3
We now discuss the Zariski Cancellation Problem.
Zariski Cancellation Problem
We know that for a non-zero real number r, a relation rv=r^{n+1}(=r.r^n) implies that v=r^n, i.e., r^n has the cancellation property. We also know that the implication does not hold if r=0. We frequently apply this cancellation property of non-zero real numbers in any work involving basic algebra. We also need to remember always that 0 is not cancellative. Cancellation questions also arise for mathematical objects like affine spaces in place of elements, with equality being replaced by isomorphism.
A fundamental cancellation question on affine spaces is the Zariski Cancellation Problem which asks whether every affine n-space K^n over a field K has the cancellative property. That is, if \mathbb{V} is a space defined by a system of polynomials over the field K such that \mathbb{V} \times K is isomorphic to K^{n+1}, does it follow that \mathbb{V} is isomorphic to K^n? For n=2, the problem may be visualized as follows: if the cylinder over an algebraic surface V is isomorphic to the 3-space K^3, then is the surface V necessarily isomorphic to the plane K^2?
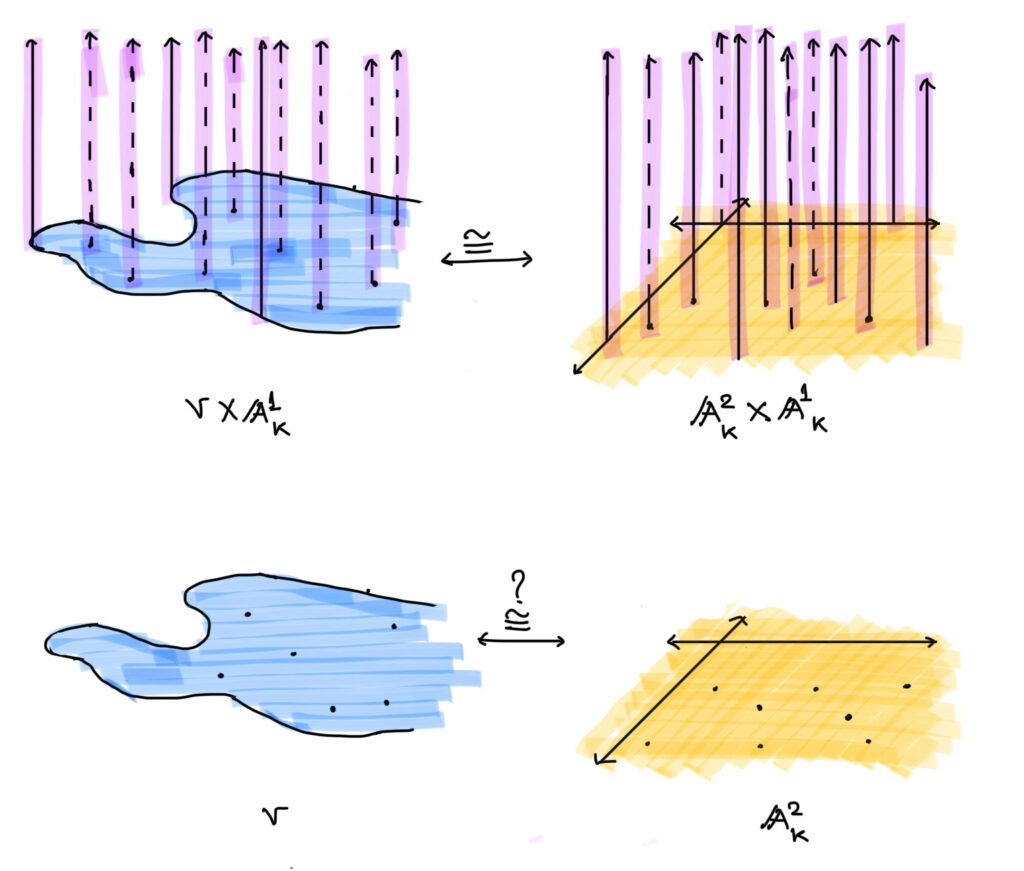
Affirmative answers were provided for the affine 1-space K (also called the affine line) by Abhyankar–Eakin–Heinzer (1972) and for the affine 2-space K^2 (also called the affine plane) by Fujita–Miyanishi–Sugie (1980) when K is of zero characteristic and Peter Russell (1981) when K is a perfect field.
The Zariski Cancellation Problem has been influencing mathematical developments for more than seven decades. For instance, C.P. Ramanujam’s topological characterization of {\mathbb{C}}^2, one of the high-points of Indian mathematics during the past 60 years, was inspired by an attempt to show that the affine plane is cancellative. This was followed by M. Miyanishi’s algebraic characterization of the affine plane (1975) which led to the establishment of the cancellation theorem for the affine plane, a result that has been of enormous technical aid for researchers.
But what happens in the case of the affine 3-space? Does the cancellation property hold? There was no further answer for more than three decades, though the period witnessed mathematical activities around this question and closely related problems. We highlight important developments due to the Japanese mathematician Teruo Asanuma who was a regular visitor to TIFR and ISI Kolkata from 1994.
Asanuma did deep and pioneering work in the 1980’s in another important area of affine algebraic geometry known as `affine fibrations’. This area investigates the structure and properties of an `R-algebra’ gleaned from information about its fibres over the base ring R. During 1987–94, Asanuma constructed and studied a k-algebra A over a field k of positive characteristic, the ring A being defined by a relation of the form x^m y=f(z,t), where f(Z,T) is a certain `non-trivial line’ in k[Z,T] as defined previously. This pivotal ring A is known as an `Asanuma threefold’.
Improvising on certain expansion techniques of Abhyankar–Moh, Avinash Sathaye had shown in 1983 that when a field k is of characteristic zero, then any {\mathbb{A}}^2 fibration (an algebra whose fibres are polynomial rings in two variables and have some basic properties) over the polynomial ring k[X] are polynomial rings in two variables over k[X]. The `Affine Fibration Problem’ asks whether the result extends to all {\mathbb{A}}^n fibrations over polynomial rings of all dimensions.
Asanuma showed that the above theorem of Sathaye does not hold when k is of positive characteristic; for he proved that the Asanuma threefold A is an {\mathbb{A}}^2 fibration over k[X] but not a polynomial ring over k[X]. He then asked the question whether the Asanuma threefold is a polynomial ring (in three variables) over k.
Asanuma showed that if the answer to his question is Yes, then there is a counterexample to another important problem on affine spaces called the `Linearization Problem’ in positive characteristic; but if the answer is No, then the Asanuma threefold A is a counterexample to the Zariski Cancellation Problem. Peter Russell popularized this dichotomy as `Asanuma’s Dilemma’. He popularized the simplified case m=1 of the Asanuma threefold, i.e., the ring defined by xy=f(z,t). But for nearly two decades there was no resolution of the dilemma.
Neena’s outstanding postdoctoral research at TIFR
We now return to Neena’s research. During her three and half years as a PhD student, apart from doing research on Laurent polynomial fibrations for her thesis and working with me and Onoda on another topic called `{\mathbb{A}}^1-patch’, she had been making an extensive study of research papers on other topics. One such topic was `{\mathbb{G}}_a-actions’. In characteristic zero, the `{\mathbb{G}}_a-actions’ are usually studied through `locally nilpotent derivations’ and in arbitrary characteristic, they are often studied through a more technical concept known as `exponential maps’.
There were exciting developments on locally nilpotent derivations from the 1990’s, resulting in a huge amount of research literature. L. Makar-Limanov opened up a new horizon in affine algebraic geometry when he used the tool of `locally nilpotent derivation’ to show that a certain three-dimensional ring over \mathbb{C} defined by Peter Russell, known as the `Russell cubic’, was not isomorphic to a polynomial ring in three variables over \mathbb{C}. Using exponential maps, A. Crachiola extended the result over any field. Makar-Limanov had defined a new concept pertaining to locally nilpotent derivations (later extended to exponential maps), now known as the Makar-Limanov invariant, to distinguish between the Russell cubic and the polynomial ring. All hitherto known invariants and properties had failed to distinguish the two rings. Makar-Limanov and Crachiola also gave a new elementary algebraic proof of the cancellation theorem for affine planes.

Neena had studied the literature in this fertile area, especially the techniques developed by Makar-Limanov and Crachiola. It also helped that Bhatwadekar had delivered a series of survey lectures on locally nilpotent derivations at ISI Kolkata in November 2007, highlighting the above developments, and when Neena joined me as a PhD student, she studied my notes of the lectures.
I also encouraged Neena to study Asanuma’s deep work on affine fibrations; although not much development had been taking place in that direction and therefore there was a tendency among researchers to not dwell on it. Again, it helped that Asanuma was to visit ISI in 2011 and therefore Neena had an additional impetus to get immersed in his work.
With her studies on the above two streams, Neena began to wonder whether the new techniques on {\mathbb{G}}_a-actions developed by Makar-Limanov and Crachiola could be applied to resolve the Asanuma Dilemma about the Asanuma threefold. When Asanuma visited ISI Kolkata during February-March 2011, Neena broached the topic. Asanuma was shocked that a novice in research was thinking about the longstanding Zariski Cancellation Problem which was considered a notoriously hard problem by some of the best mathematical minds. Affectionately, he cautioned in a musical tone, “it is v-e-e-e-e-e-r-y difficult”. He felt that the raw youngster should apply herself to reasonably tractable problems rather than waste her time on a question which, in all likelihood, will not result in any concrete research output.
In May 2012, Neena joined TIFR as a postdoctoral Visiting Fellow. Bhatwadekar had retired from TIFR a year earlier and joined the Bhaskaracharya Pratishthana at Pune. At some point Neena took up her earlier idea and plunged into the Zariski Cancellation Problem through Asanuma’s Dilemma using {\mathbb{G}}_a-actions. Her approach involved repeated applications of some homogenizing techniques involving judicious assignments of weights to generators of several intermediary rings. Finally, sometime in July, she arrived at the “Eureka” moment: she succeeded in showing that a certain invariant of an Asanuma threefold called the `Derksen invariant’ was not the Derksen invariant of a polynomial ring! This invariant too is defined by exponential maps. It is interesting to note that Neena considered relations of the type x^m y=f(z,t) for m>1 and not the simpler form xy=f(z,t) popularised by Russell; the consequent asymmetry helped her achieve her goal! Indeed, her approach did not work for m=1. So, to summarize, Neena showed at last that the Asanuma threefold for m>1 was not isomorphic to the polynomial ring showing that the affine three space is not cancellative in positive characteristic, that is, the Zariski Cancellation Problem has a negative answer in this case.
Neena sent a draft of her proof to Bhatwadekar and me by email after which we had regular and frequent discussions on phone and email for the next few days. Her proof being too intricate I used all my research experience to help her organize the presentation in a manner that will help a reader go through the difficult steps. Her paper is short (only 10 pages) and elementary. It is accessible even to a bright undergraduate student who has aptitude for ring theory. Though full of algebraic intricacies the paper is nearly self-contained – it does not require familiarity with advanced or specialized topics. It is rare to come across such a paper in her area which is at the frontier of research and yet accessible to a student. I recommend bright students with spare time to read the paper as it will demonstrate before them at an early stage, a concrete and complete example of an outstanding research accomplishment. The paper is titled “On the cancellation problem for the affine space {\mathbb{A}}^3 in characteristic p”. It appeared in the prestigious journal Inventiones Mathematicae.4
Sometime in July 2012, she delivered the TIFR Colloquium talk on her PhD thesis. She was being congratulated for her thesis and her talk, but TIFR mathematicians had no idea of what she had quietly accomplished during that month. Finally she dropped the bombshell, sometime in late July, that she has solved the Zariski Cancellation Problem for the affine 3-space in positive characteristic. In spite of her brilliant academic and research record, the first reaction was of sheer disbelief. Bhatwadekar and I confirmed that we have indeed checked the details. The official confirmation from the journal Inventiones Mathematicae, where she had submitted her paper in September 2012, arrived in January 2013.
Both Onoda and I visited TIFR in September 2012. A special seminar was arranged during the month where she presented her breakthrough work. The seminar room was full and the TIFR experts listened with rapt attention. There was almost a festive mood in the air at Neena’s success in resolving the famous problem. Dipendra Prasad, the then Dean of School of Mathematics of TIFR, arranged a special official lunch for Neena to celebrate the happy occasion; Onoda, Ravi Rao and I were the invitees.
Neena was selected for the inaugural Saraswathi Cowsik Medal of the TIFR Alumni Association; the award was presented to her in 2013 on TIFR Founder’s Day (30 October). Her solution to the Zariski Cancellation Problem was one of the main themes in an International Conference on Polynomial Automorphisms and the Jacobian Conjecture that was organized by Arno van den Essen and Wenhua Zhao at the Chern Institute of Mathematics soon after her result was announced.
I feel it was very appropriate that Neena had made her first breakthrough on the Zariski Cancellation Problem during her stint at the TIFR. First, she may be considered as a product of the famed algebra school at TIFR. I had been a student and collaborator of Amit Roy (1940–2010) and Bhatwadekar of TIFR for several years and I must have transmitted something of their algebraic styles and skill when I was mentoring Neena. My role here reminds me of the Arab transmission of Indian arithmetic. Further, Neena had direct interactions with Bhatwadekar himself. Second, TIFR has a rich legacy of solving cancellation problems for quadratic spaces and projective modules where Amit Roy, Bhatwadekar and their students and collaborators were involved.

Neena’s outstanding postdoctoral research at ISI
Sometime in December 2012, Neena Gupta returned to ISI Kolkata with the INSPIRE Faculty Award. After the acceptance of her first paper on the Zariski Cancellation Problem in Inventiones in January 2013, she was flooded with congratulatory mails from experts and even job offers. Hardly had the excitement faded, when she announced her follow-up work. This was a deep insightful theory on the class of threefolds defined by a relation of the form x^my=F(x,z,t). The theory culminates in an amazing theorem which establishes the equivalence of ten statements and thereby gives a unified treatment of several apparently different-looking questions of fundamental importance which had been of long interest to mathematicians, including the Zariski Cancellation Problem, the Abhyankar–Sathaye Conjecture, and the Affine Fibration Problem.

Soon thereafter, she showed that the Zariski Cancellation Problem has a negative solution for any affine space of dimension greater than two when the underlying field is of positive characteristic.

Neena’s thesis had already given early evidence of her flair for both these qualities. Her Inventiones and Compositio papers of 2014 are grand examples of (vii) and (viii) respectively. After a mathematician solves a longstanding problem through sheer ingenuity, it is usually other mathematicians who gradually develop, over a period of time, a good theory which provides a deeper understanding of the underlying principles. It is rare to come across a researcher like Neena who, after solving a celebrated problem by sheer algebraic ingenuity, herself builds, in a very short time, a path-breaking general theory that provides easy solutions to previously open problems and a simple recipe for solving more of such unresolved problems in future.
Miscellaneous episodes
During the international conference at KSOM in 2014, when Bhatwadekar, Neena and a prominent Polish mathematician were travelling by car to the conference venue, the Polish mathematician struck a conversation with Neena. During those days, Neena’s girl-next-door appearance could be mistaken for an undergraduate student. At some point, the Polish mathematician asked her, “Do you know that an `Indian’ has recently solved the Zariski Cancellation Problem?” An amused Bhatwadekar immediately quipped, to the astonishment of the Polish mathematician, “That Indian is sitting next to you!”
Neena felt doubly happy at the tag `Indian’. Later, when she was awarded the Ramanujan Prize at the ICTP, it was a proud occasion to celebrate Indian contributions. In his brief speech introducing Neena’s work, Ng\hat{\rm o} Bao Ch\hat{\rm a}u recalled that there were two streams in algebraic geometry where Indians have made major contributions: one pioneered by M.S. Narasimhan, and the other, pioneered by S.S. Abhyankar, and pointed out that Neena’s work belongs to the Abhyankar school. He was spot on. One can indicate an arrow of transmission: Abhyankar \rightarrow Sathaye \rightarrow Bhatwadekar and Roy \rightarrow Amartya Dutta \rightarrow Neena Gupta.

During 2013-14, mathematicians from renowned institutes like CMI, TIFR, IIT Bombay, wanted her to join their institutes. She was invited by CMI to present her work. Late C.S. Seshadri of CMI had fond memories of interactions with Fields Medalist H. Hironaka; the difficulty of the Zariski Cancellation Problem had once come up during their discussions. Naturally, Seshadri was keen that Neena join CMI. She got job offers from IIT Bombay and TIFR and the Director of IIT Bombay personally rang her to try to convince her that she should join IIT Bombay. After a freeze on recruitment was lifted, she got an offer from ISI Kolkata, where she joined as an Assistant Professor in June 2014 and continued her research.
In June 2015, Neena got married to Vishal Saraogi who has been supportive of her. A year later she was blessed with her daughter Manya. After a break, Neena has again been prolific in her research and has been mentoring several doctoral and postdoctoral researchers. In recent years, she and her students have made various generalizations of her earlier results to obtain affirmative solutions to the Abhyankar–Sathaye Conjecture for various classes of polynomials which are linear in one of the indeterminates.
Alongside her research and other mathematical duties, Neena has been performing all her family responsibilities, especially taking personal care of her little daughter. She is deeply religious and personally I feel that rigour, dedication and intensity in her mathematical life have come to her naturally from the meticulousness, discipline and devotion in her religious life from early childhood. It has been deeply rewarding to be a witness to the rapid evolution in her maturity as a human being, alongside her rapid progress in mathematics.
Epilogue
For the book Vigyan Vidushi, I had been invited to write the biographical sketch of Neena Gupta. During the book release programme at Vigyan Bhavan, New Delhi, on National Science Day [28 February] 2023, a gentleman remarked to me in a congratulatory tone that it is rare to come across someone writing about his student! Indeed, it must be a rare privilege accorded to a mentor that his student becomes famous in such a short time that he is asked to write about her inspiring journey.
And, I agreed to write on Neena’s life and achievements as I felt it would act as an inspiration and motivation for youngsters in India.\blacksquare
Footnotes
- https://www.infosysprize.org/laureates/2024/neena-gupta.html. ↩
- Bhāvanā, in its October 2021 issue, featured a story about Emmy Noether in sketches. https://bhavana.org.in/emmy-noether-her-story-in-sketches/. ↩
- Séminaire Bourbaki, 37 (1994-1995) 295–317; also available at https://eudml.org/doc/110203. ↩
- Inventiones Mathematicae 195 (1), 2014, 279–288. ↩
