
Daina Taimiņa, born in 1954, in Latvia, probably best exemplifies this great synergy between mathematics and the arts, a synergy that affords many exciting possibilities. As a maths educator, Daina has employed the fiber arts and exploited the mathematical themes underlying them as an effective teaching device. She pioneered the use of crocheting models as a potent medium to explain the idea behind the geometry of the hyperbolic plane, which was until then not readily visualisable. Her unique book Crocheting Adventures with Hyperbolic Planes won the 2012 Euler Book prize awarded by the Mathematical Association of America1 and also another interesting accolade: the 2009 Bookseller/Diagram Prize for Oddest Title of the Year!2
Daina’s fiber artwork and crochet models have made their way into numerous mathematical museums and have been showcased at many art galleries around the world as exhibits. Notably, Daina’s ideas served as the genesis of the Crochet Coral Reef project that came about through her collaboration with Margaret Wertheim and the Institute of Figuring, a project that has now grown in scope, given the underlying currently significant theme of global warming and climate change.
In this freewheeling interview, Daina Taimiņa recounts her transformative childhood years, growing up in Latvia, her unexpected doctoral degree in theoretical computer science and her later evolution into a mathematical artist and geometer.
Daina Taimiņa’s work is testimony to the fact that women bring more than just diversity and excellence to mathematics, rather the feminine aspect is in itself a quintessential manifestation of the very nature of mathematical ideas, ideas that can only be completely realised and propagated by the perspective that women bring to the mathematical world.
First of all, a very warm welcome on behalf of Bhāvanā. Let us start at the very beginning. You were born in Riga, Latvia in 1954. Tell us a bit about your childhood and also about your Latvian heritage.
DT: I was born nine years after WWII, and five years after the second largest deportation of Latvian intelligentsia by the Soviets. Both my parents had left Doles Sala (an island on the river Daugava not far from Riga) and moved to Riga to find jobs in the city. During my first six years, our family lived in a small room, sharing a large apartment with other people. I was the only small child in that apartment and I was loved by everybody. Across our room, which was facing north and was always semi-dark, there was a room occupied by a professor. For political reasons, he could not hold any official position–-he used to work for the government before the Soviet occupation, and had had encounters with the KGB. Since he was working from home, I spent a lot of time with him. To keep me busy he taught me to read before I turned four. Since then, I have fallen in love with books. He also gave me very valuable advice: “Keep learning! You may lose everything, but nobody can take away what is in your head.’’
How were your schooling days? Do you have any notable memories from that time?
DT: Thanks to my “babysitter” professor Skuja, I was well prepared for school, except that I had to learn to write in cursive. In second grade, I got into a fight with a maths teacher because she claimed I was interrupting her class. My parents were called to the school, and at the teacher-parent meeting, the teacher was asked how I was behaving in her class. She said that she could barely ask a question to the class when I would be already answering it. Then I was asked why I was doing that. I honestly answered–-“Because I want to learn something new, it is too boring to keep repeating the same thing again and again for those who cannot get it”.
Were you interested in maths from an early age?

DT: I found maths interesting when I was in fifth grade, and we had a wonderful maths teacher. He was always prepared to give me something else to do while the rest of the class did routine exercises. I was not alone in that because there were two boys who also had the same problem that I did. For me, it was a matter of friendly competition to get results faster.
So you were precocious. Was there anyone in your family or friends, or a teacher who motivated your interest in maths initially, say, from high school? Or was the interest more organic and gradual?
DT: I was very lucky from grade five onwards to have good maths teachers. The best teacher I had was in high school–-Alfrēds Grava–-showed us how beautiful geometry was. All his teaching style was problem-based. He would come into class and say, “You know, this morning while commuting, this problem came to my mind. Let’s see if we can solve it.’’ We would start and then he would stop and say, “Oh! At this point, we could use a theorem, but I haven’t told you about it. Let us first prove that.’’ He was also an author of several maths textbooks and problem books. He had amazing freehand drawing skills.

Jeff Weeks, who shares your fascination for the hyperbolic world, mentioned in an interview to Bhāvanā last year that reading the book “Flatland” made him fall in love with geometry. Did you too have any such favourite books that shaped your interests growing up? Did you read a lot by the way, or were you more of the `outdoors’ type?
DT: I was reading Russian translations of Martin Gardner’s books. They were interesting, but I was more fascinated with the world of literature. We had many books from all over the world translated into Latvian. Of course, at that time I didn’t know that those translations were not fully authentic–-some original text was censored. One of my favourite books was Dickens’ David Copperfield. My favourite book in middle school was Resat Nuri Guntekin’s Calikusu (The Wren). I was fascinated by Feride’s (the lead character) determination to be a teacher. In high school, the whole class knew almost by heart Jerome K Jerome’s Three men in a boat and often quoted it at appropriate moments to tease classmates. I loved reading biographies and books about travel. It was so fascinating to read about Marco Polo. I also love poetry and I still have a few small books of Rabindranath Tagore in Latvian. My parents had a copy of Rudyard Kipling’s The Jungle Book which I read at about age eight. Only later I learned that he had written poems, and his poem If–- still is one of my favourites.
Latvia, at the time, was under Soviet occupation. Did that have any noticeable (positive or negative) effect on your formative years, particularly in educational aspects?
DT: I must admit the most positive effect on my education–-it was free then. My parents would not have been able to pay for my education. As for the rest–-we were young, fascinated with the poetry of that time, which taught us to understand the hidden meaning behind words. To pass censorship, the poem could be apparently about nature, but we would know what each symbol meant. In my formative years, I learned critical thinking by comparing what was in the news against what was in reality.
Incidentally, what was the medium of instruction during the time of your education? Was it Latvian?
DT: From grade one up to my graduate studies, all of the instruction was in my native language Latvian. Those whose native language was Russian had their instruction in Russian. All textbooks I had in school were in Latvian. At the university level, textbooks were in Russian because there would not be enough of a market for books in Latvian. However, university instructors would write their own teaching materials in Latvian, and they were published by the Latvian University Press. These were of very poor printing quality, and essentially cheap paper brochures, but very much appreciated by students.
I must admit the most positive effect on my education—it was free then
Did you feel that learning maths in your native tongue was beneficial for honing your intuition and understanding? I ask this because, with the new national education policy here in India, there has been an increased debate on learning subjects like mathematics in one’s native tongue.
DT: Certainly, yes. See, if your instruction in any subject is not in your native language, then first your brain has to translate it into your language and then you must translate your answer back. And the level of this other language in itself, has to be pretty advanced. If M.~Gardner’s books wouldn’t be so engaging, I wouldn’t read them in Russian. It took me some time to start reading other popular maths books in Russian, written by excellent mathematicians.
As a precursor to your later work, were knitting and crocheting something that you enjoyed even as a kid? There seems to be a long tradition of handicraft making and even handicraft education (Rokdarbi) in that region.
DT: Yes, handicrafts were part of the school curriculum until very recently. I learnt only basic handicraft skills in school. Most of my advanced skills came from practical purposes–-to make my own clothing. For example, at school, we had to wear navy blue school uniforms. However, we could wear some sweaters when it got cold. That was where we could make something unique. I loved knitting. I taught myself to crochet in order to finish my knitting projects.
So you were always handy with the needle. Latvia has a vibrant folk history, drawing in general from the rich Baltic mythology. Did that hold a fascination for you at any point?
DT: Yes. I have knitted things with Latvian ornaments in them. I loved cross-stitch tablecloths, or pillows with Latvian ornaments. I am very interested in comparing geometric symbols from various cultures and finding their similarities–-for example, the following symbol:
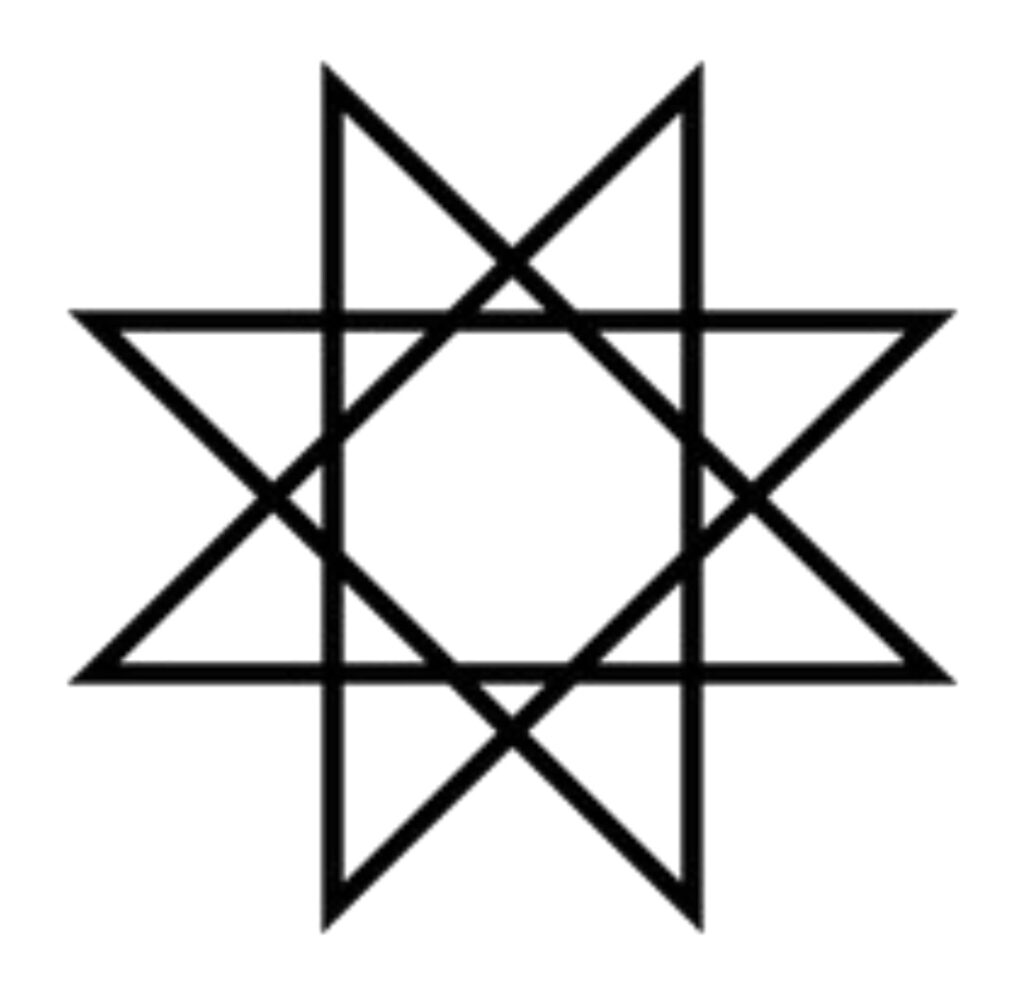
That is an interesting symbol, an octagram. What is its significance in Latvian culture?
DT: It is a symbol of the Morning Star–-Auseklītis . In Latvian mythology, it is believed that wearing it protects you from evil. It was a symbol of Atmoda –-in 1989-1991, when Latvia was gaining independence from the former Soviet Union. Recently I learned that this symbol could be traced to ancient Mesopotamia as a sign of Goddess Ishtar or Inanna.
In the Hindu culture, a variant of that symbol is associated with the Goddess Lakshmi. Incidentally, the Latvian language along with Lithuanian, are commonly claimed to share their roots with Sanskrit. In fact, there seems to be some shared mythology of Gods too. For instance, Latvian culture has the notion of the Divine Twins or Dieva Dēli (Sons of Dievs) and the closely related Ūsiņš, which seemingly corresponds to the Vedic era Ashvins (sons of Dyaus, and the horsemen). The resemblance seems to be even more striking when looking at the Lithuanian equivalent where they are called Ašvieniai (the horse twins). In Latvia, Ūsiņš day heralds the arrival of summer?
DT: Yes, there are similarities between Sanskrit and the Latvian language or Latviešu valoda . For instance, the Latvian for “Who are you” is “Kas tu esi” and it is “Kas tvam asi” in Sanskrit, and “night” in Latvian is “Nakts” while the Sanskrit equivalent is “Naktam”. There are probably many others. I only became aware of it when I started university from what I recall. I had a friend at the university who was studying Latviešu valoda and literature at the time.
As for Ūsiņš day, it is in April, and not summer yet in Latvia. It is a spring festival that marks the beginning of shepherding–-animals, mostly horses, are let to go to pastures, and the green season starts. But yes, in some ways, it does herald the beginning of warm weather. With climate change, not anymore, it can get warmer earlier.
You graduated from the University of Latvia as a mathematics and maths education major with a cum laude. What topics in mathematics did you really enjoy or connect with the most, during your graduation days? Did the maths education aspect motivate your later pursuits?
DT: I chose to study mathematics because it seemed to be the least political subject (later in life, I learned I was wrong) and I wanted to become a teacher. As for topics in maths–-I liked geometry, analysis; algebra seemed dry and formal. My passion during university was not maths. I wanted to be a teacher, and for me, it meant to know much more than your own subject. I was not planning on doing any further graduate studies.
I see. But then you did your doctoral studies in theoretical computer science under the renowned Latvian mathematician and computer scientist Rūsiņš Mārtiņš Freivalds–-of the Freivalds algorithm fame. Tell us a bit more about how this choice of theoretical computer science transpired? Was it a conscious one?
DT: When after graduating from the University of Latvia, I was invited to stay on as an instructor, I agreed. But then I faced a need for a degree. I tried to do something in education, but that was a bad experience–-too much Communist ideology was required. I dropped it. Then I worked in the history of mathematics, and did some research, but I needed to access some archives outside the Soviet Union, which was denied.
I also love poetry and I still have a few small books of Rabindranath Tagore in Latvian.
I first met Freivalds briefly in 1976, when I was an undergraduate. I later met him again in May 1980. The Soviet Union, of which Latvia was then a part, was celebrating the thirty-fifth anniversary of the end of WWII and the University of Latvia track and field team (of which I was a part) proposed to perform a relay run of about 500 km. Since it was a highly politicized event, for each region that the run was going through, some senior member from the University of Latvia was to be present. When I finished one of my parts of the relay in Latgale and was getting into our bus, I was greeted by a man who said: “You should stop running around, and should start serious work.” It was Rūsiņš Mārtiņš, who was in charge of that region. I replied, surprised: “What do you mean by that?” and he told me “You have potential; you should come to my seminars.” So I met Prof. Freivalds by accident. I did not even know what he was doing, when he suggested that I attend his seminars. I was still in doubt when the chair of my department heard about this invitation, and made a remark that I was too stupid to be Freivalds’ student. That was a push for me to prove that he was wrong.

Freivalds was known to be a prolific researcher. What are your memories from your doctoral research period, and from your interactions with Freivalds? How did you cope with the rather steep learning curve that probably resulted from this unexpected foray into theoretical computer science?
DT: At that time, I was teaching calculus and geometry for physics undergraduates and prospective mathematics teachers, and was a part-time high school teacher myself, and had a part-time job on a grant about mathematical methods in nuclear physics. After some hesitation, I went to the first seminar, just to realize that having no background in computer science, I could not understand a thing. I was ready to leave but Freivalds said that I should not do that after just one meeting, and that I should continue to come to the seminars.
It was a challenge because I lacked all introductory computer science courses. So I was taking classes with computer science undergrads. It took me ten years from our first meeting to the degree.
My advisor also required regular weekly meetings with him, so I could catch up on courses I missed as an undergraduate–-algorithm theory, automata theory, etc. Our meetings were held in his office, and he usually explained a new notion, then assigned to me about four or five problems, and I had a week to work on them. I am not sure that Rūsiņš even knew that in the US such an approach is called the Moore Method, nor did I. For me, it was Freivalds’ method of teaching computer science.
Just to be in the same room with such a legend [Kolmogorov] was memorable
That’s really inspiring! You also spent a semester in Moscow during that period.
DT: I spent a semester at Moscow State University as a young university instructor in order “to improve my qualification”. It was expected that we take some maths classes and also attend lectures in “scientific communism” etc. I think I showed up for some of those large required classes to make sure I had attendance, but have no memory of what was lectured. Prof. Freivalds gave me names of mathematicians I should take classes from. I really enjoyed the lectures of Prof. Vladimir Uspensky, who taught the theory of algorithms, and Semenov’s class in automata theory. They both were also participants of the Kolmogorov seminar which I attended. Kolmogorov himself came to the very first one. I think he had recently suffered a stroke, because his speech was hard to understand. Semenov was acting as an interpreter. Nevertheless, just to be in the same room with such a legend was memorable.
The closest place to reach by overnight train was Minsk, and that is why I defended my thesis there
Your thesis was on the `Behavior of Different Types of Automata, and Turing Machines on Infinite Words’, which you finished in 1990?
DT: In other words, it can be described as how to make a decision knowing only a part of some information (infinite word), how long this part should be, and what is the probability that your decision is correct.
You actually ended up with a Ph.D from the National Academy of Sciences of Belarus after defending your thesis in Minsk, although you studied at the University of Latvia.
DT: Actually, I finished writing the first draft of my thesis on November 27, 1987. On December 1, 1987, my oldest daughter was born. It delayed the time of my formal thesis defence. In those days, the defence of the thesis in mathematics and computer science had to be outside Latvia in certain accepted places. I was trying to find a place that would accept me. But then the whole Soviet Union started to crumble, and it was complicated to find the board for the defence of my PhD thesis. By then, I was pregnant with my second child, and was not allowed to fly for medical reasons. The closest place to reach by overnight train was Minsk, and that is why I defended my thesis there. There were fifteen voting members, each with one white and one black ball. In order to pass, there had to be at least eight white balls. For me, there were fifteen.
From working on automata to hyperbolic geometry, how did that shift come about?
DT: Another accident. 🙂 I kept teaching in the same department as before, and had various other courses; also, I was advising several masters theses in maths education. I had to leave computer science because it would take too much time, and I had two small children.
Then you moved to Cornell in 1996. But before that, you met your future husband David W.~Henderson, himself an accomplished geometer, at a geometry workshop in Italy.
DT: It was not a simple workshop–-it was an invitation-only ICMI Study Group “On the teaching of Geometry for the 21st century”. I was representing Latvia. David gave the last plenary lecture, after which I went to him with an example. That started our collaboration on a paper, which is the only one we never finished.

And a whole new adventure started in a workshop that you attended at Cornell in 1997! Bill Thurston provided the rudiments of a paper model of the hyperbolic plane in his book. Was Thurston the first to come up with that sort of construction? Can you tell us a bit about the history of such hyperbolic models? What made you anticipate a better model, a crochet one?
DT: Thurston came up with a paper model idea when he was a senior in college. He said he wanted to see how a hyperbolic plane looks. He did not know that Beltrami had made a paper model in 1868. Because a paper model is a physical model, and can be handmade, I was just thinking of using a different medium that would impart the model more durability, and playability.
Your breakthrough made it possible for the first time to actually get a very good physical realisation of what was until then an abstract mathematical construct. That crocheting is something one would rarely consider as a source of mathematical ideas makes it all the more surprising and remarkable. For the benefit of our curious readers, can you give a brief idea of the “crocheting algorithm” at play?
DT: In order to get this curly surface, the number of stitches in a row should increase steadily–-for example, adding one more stitch after each five. Keeping this ratio, the number of stitches will increase exponentially.
I was just thinking of using a different medium that would impart the model more durability, and playability
So the model that one gets is a surface of constant negative curvature. But then we come to Hilbert’s theorem that a complete smooth surface of constant negative curvature could not be embedded in the three-dimensional Euclidean space. How does this model work around that obstruction?
DT: That issue and some others are well discussed in a Mathematical Intelligencer article.3
Thurston was probably very happy once he knew about it. You have often attributed Bill Thurston as a major influence and support, and he wrote an insightful foreword for your book. Tell us something about your enriching association with him.
DT: I was attending his seminars, classes. Not that I understood much but I liked to watch Bill think at the board, and come up with ideas, and then correct them. He valued what I was doing at the time when some others were not taking me seriously. I am very grateful for his foreword to my book which otherwise wouldn’t be taken seriously either. Also, John Conway’s endorsement of the book is very precious to me.

Of course, we have to talk about your book, Crocheting Adventures with Hyperbolic Planes, which still remains one of its kind. Along with Jeff Weeks’ Shape of Space, I find it one of the most beautiful books concerning geometry available in that it literally gives you a physical feel for the topic at hand. Can you share a bit about how the book came to be realised?
DT: It was Vicki Kearn from Princeton University Press who, once after my talk, suggested that I should write a book. I submitted a book proposal, and it had two reviews that were diametrically opposite. Then I met Klaus Peters who asked me about the book. David suggested that I write it first because nobody really understood my vision for this book–-because they had never seen anything like it before. My inspiration was Joanne Harris’s cookbook The French Kitchen that had beautiful photos, stories and recipes (The author is best known for her novel Chocolat). Since English is my third language, it was easier for me to tell a story and show how with pictures, which I both drew, and photographed myself.
 |
 |
Both yours and David Henderson’s philosophy on maths education is a revelation. To give some context, you co-wrote an introductory book on geometry Experiencing Geometry: Euclidean and Non-Euclidean with History along with Henderson, the fourth edition of which came out last year. The book, true to its title, is unique in its treatment of the subject as it talks about geometry as an experience to be sought in the making of machines, paintings and in nature. Is that also how the both of you approached your teaching?
DT: Yes, that is actually how we met–-we started to talk at that ICMI Study I mentioned before, and realized that we both have similar teaching philosophies. When we met in 1995, David had just received the first few printed copies of Experiencing Geometry. It was the first edition. I worked with him on the subsequent editions of the book. The fourth edition, which is published, and available as open-source,4 is in his memory.
There are models that are inspired by nature
A similar theme is seen in Henderson’s other book on differential geometry, to which you also contributed writing. In fact, there is a particular exercise to show the intrinsic nature of the Gaussian curvature, or in other words, it acts as a proof of the ‘Theorema Egregium’ which I have not found in any other book on differential geometry. The proof is also personally the most enlightening, among all the other proofs available. Tristan Needham, who also discovered it independently much later, expresses similar sentiments in his newest book on differential geometry, and that, apparently, neither Marcel Berger nor Roger Penrose was aware of it when he wrote to them.
DT: That proof is a hundred percent David’s–-he was proud of that result. I am glad to see that it is now recognized as unique.

You taught at the University of Latvia for almost twenty years for students at various levels. What were the subjects that you taught and did you have an affinity for using hands-on activities to supplement your teaching activities even then?
DT: I taught various geometry classes, calculus, history of mathematics, psychology of mathematical thinking. At the time, it was not very hands-on. I was sometimes blamed by colleagues for teaching too simply, not as formal as required. I was just trying to make the material more accessible to students.
You also later taught at Cornell and went on to engage workshops and give lectures around the world. How has your teaching evolved since your time in Latvia over the years, and how do you adapt yourself to dealing with an assorted audience with varying levels of mathematical knowledge?

DT: I was an adjunct faculty at Cornell for most of the time I was teaching there. It means that sometimes, even a few days before the semester starts, I don’t know what I will be teaching, if anything. That means I was teaching various courses and at various levels–-freshman calculus, multivariable calculus for engineers, honours calculus, geometry and history of mathematics for seniors, explorations in mathematics for those who were scared of maths but had to take at least one maths class to graduate. One year I was teaching a supplemental course in calculus and for that, I was hired by the Learning Center. One of my Maths Department colleagues told me that he got a phone call asking whether I will be able to teach there. He had answered: “What a question! You will be lucky–-she can teach anything!’’

So how do you approach your work on making these mathematical models? What is the accompanying thought process when you decide to do something new for an exhibit?
DT: It really depends on the exhibit–-how large the model should be, and what materials are available. Using wool is very tempting and feels good working with, but it is an expensive material. I like to try new materials.
What non-mathematical themes or motifs inform your crocheting models the most? Do you just look around for inspiring ideas in nature, or is it more of a calculated preparation?
DT: There are models that are inspired by nature, but most of the time it depends on what materials I have available. I do not do any calculated preparation.

The use of crocheting or more generally knitting as an effective tool in communicating mathematical ideas seems to be finding a great amount of traction in modern maths teaching. Of course, this extends to other manual activities. This is also in line with the opening quote of Confucius5 in your book. But do you see these practices as just effective teaching tools, or as something with the potential to draw a larger majority of the populace, especially women, into mathematics courses, through something more down to earth and relatable?
DT: There is some psychological effect to these models–-they are made by hand and therefore feel more accessible. They are tangible, real, even if they are revealing information about abstract spaces. Mathematicians have been making similar models to understand their problems for a long time.
The fusion of art with mathematics does seem to make mathematics itself a very stimulating and enjoyable activity. Given your handy background as an artist and a mathematician, how do you view this relationship between art and mathematics?
DT: You know Einstein’s quote: `The most beautiful experience is the mysterious. It is the source of true art and science’. I think the common link between art and mathematics is creativity. That would be my short answer. I could give a whole talk on this topic but that would be too long here (smiles).6

So apart from crocheting and teaching math, you are also a painter.
DT: I wish I had more time for that. I was told in school that I can do anything but art. So all my life I thought that I was bad at art until I took a watercolour class and learned something. I really took that class because I wanted to experience what students who are told, and sadly, end up believing, that they are bad in maths, experience in my classes. It turned out that it was only the watercolour techniques that I had to learn. At university, besides other traditional geometry courses, I had also taken a course in descriptive geometry, as well as a short course on how to draw three-dimensional geometric diagrams–-both these latter courses contained a lot about perspective.
What has been your most satisfying and favourite artistic project so far?
DT: It was creating an installation “The Cloud of White Thoughts” for a 2014 exhibit in Latvia. In Latvian, “white thoughts” poetically means thinking good thoughts. I told the participants not to buy new material but to look for something around them that they can use because you cannot buy those good thoughts, you have to create them from what you have. Continuation of this was last year’s installation for Riga Biennale “Dreams and Memories”–-there were more colours in that. Ironically, my dream was to create this big installation, but because of the Covid pandemic, I was not able to go to Riga, and it was displayed, though not in the way I envisioned. That is how my own dream became a memory. My whole idea for this work was to create it in memory of my husband David Henderson, without whom I wouldn’t be what I am now.

That’s heartening to hear. On a side note, I hear that you visit Latvia almost every year. What do you love most about the Latvian culture or the Latvian way of life?
DT: Language, food, theatre, nature–-most of my life, I lived in Latvia. It is my birthplace. It is hard to name just one thing in particular.


