
Pavaman Murthy, an emeritus professor of mathematics at the University of Chicago, is known for significant contributions to algebra and algebraic geometry. One of the very early batches of students entering the famed school of mathematics of TIFR Bombay in the late ’50s, Pavaman, as he is known to his friends and colleagues, did his Ph.D. with C.S. Seshadri. Returning from an exciting stint in Paris just then, Seshadri introduced Pavaman to the impactful seminars of Grothendieck and Serre that sparked his creative mind to telling effect. Pavaman later dropped anchor for life in Chicago, already home to another illustrious TIFR alumnus Raghavan Narasimhan. A scholar with a passion for avocational pursuits as disparate as Marxism, Urdu ghazals and long-distance running, Pavaman’s stature as a distinguished mathematician, and his personality as a genial mentor and a generous colleague, is in clear evidence in this interview with Purnaprajna and the foregoing warm personal essay My association with Pavaman by Mohan Kumar.
My association with Pavaman
I am pleased for this opportunity to reminisce about my friend and mentor, Pavaman. This is a brief and very personal account of my memories of our long association and what I have imbibed from him both mathematically and in my personal life.
I met Pavaman for the first time in 1978. Though thanks to many an amusing story about Pavaman, told by senior members of TIFR at the tea tables, he had already become a colourful iconic figure in my mind. One can imagine my nervousness when I first met him. But as anyone who knows Pavaman, his open-hearted friendliness is anything but intimidating.
When he returned to Chicago in the summer of 1979, I was by then an L.E. Dickson Instructor at the University of Chicago. It was a heady time in algebraic geometry – Miyanishi and Sugie had proved the cancellation of affine 2-space and Shigefumi Mori had settled the so-called Hartshorne conjecture, setting the course for the study of higher dimensional varieties. After several decades, the ensuing earthquakes are still going strong.
Till then, my knowledge of algebraic geometry was superficial. The above-mentioned breakthroughs and the active algebraic geometry seminar at Chicago stoked my interest. Both the algebraists I had hoped to interact with—Pavaman and Richard Swan—were equally comfortable with geometry and in the years to come, thanks to their influence, I too stopped distinguishing between commutative algebra and algebraic geometry.
At that time, Pavaman was interested in classifying rational singularities on rational surfaces and fortunately, I was pulled in. Frequently, I would end up in his house, well fed by his lovely and inimitable wife, Prema, discussing surfaces, occasionally trying to read the classic book by Coolidge. The excitement and carefree abandon of those days cannot be recaptured. Ultimately, we resolved the problems (some of them counterintuitive) to our satisfaction. By then, I was well aware of both his and Prema’s exceptional generosity, but what happened next was something beyond my expectation. He insisted that the results on rational double points are mine and that he would not be a co-author. I was young and perhaps a bit greedy, so I acquiesced to this.
I am also indebted to him for another passion of my life. While in Chicago he introduced me to Chicago Blues. Ever since that first blues concert he took me to at Theresa’s (a venerable institution, which has since closed down), the power of the blues is still with me today. Of course, it is another story, that after the concert, later in the night someone stole his car! Just one of the many fantastical stories about him.
A few years after I went back to Bombay, TIFR was literally abuzz with the thrilling news that Pavaman is returning! At that time, I was closest to him mathematically, so this was the most exciting news for me. His daily routine at TIFR was typical of his largesse. He would come to the office and on most days we would work together on how Chern classes determine projective modules over affine three-folds, and then late in the evening, he would go home. The best description for these evening walks home is that of the character Pig Pen in Charlie Brown comics. As he walked home, he would start collecting young people, and by the time he reached COBRA (today’s Bhaskara),1 there would be a coterie of us who would end up in his apartment. Those evenings of chit-chat, drinks and Prema’s delicious food, bring back such fond memories. Prema sometimes reminded me of Draupadi and her Akshayapatra. Their joie-de-vivre and hospitality sustained many of us.
But his elan did not diminish his rigour. When we finished our project on affine three-folds and started writing up our results, another facet of Pavaman appeared. He was laid-back in many respects, but while writing mathematics, I discovered that he was quite exacting. I have a tendency to be terse, but he would often point out what I should expand on and how precision and details helped everyone. I learned and grew up a lot during those years.
The institute, in spite of the camaraderie, always had a sense of underlying hierarchy for us younger ones. Pavaman on the other hand was not hierarchical. He would defend the younger and weaker (he may prefer disempowered) to the best of his abilities. Nothing would attract his ire than a bully and I have witnessed this oftentimes. He also made it a point to get visiting mathematicians together with the younger group, on mathematical and social grounds. I can certainly remember this with say, Abhyankar and Suslin. But all good things come to an end. After two years, he decided to go back to Chicago. I was devastated.
I will mention yet another occasion to illustrate his love of life and people. When Prema died an untimely death, despite his deep grief, Pavaman threw a party to celebrate her life. That is Pavaman.
Do not for a moment think that he is in any way grandiose. Pavaman is self-effacing and genuinely humble. I suspect that this is a reason why he did not have a fest for his sixtieth birthday, as most Indian mathematicians of his stature do. I am thankful to him for coming down for my retirement conference and even happier to see him dance to the Blues in my kitchen. Aah, that mischievous twinkle in his eye!
Though it seems unlikely that he and I will do any mathematics together in the future (wish it were not true), he will always, always, be my friend and mentor.
As a mentor, he is exceptional. As a noble human being, the mould is broken after him.
Even as we are excited to be talking to you, we begin by wishing you many more years of sound health and happiness. On behalf of team Bhāvanā, here is a warm welcome to you Pavaman. We would like to hear about your ancestral background and your parents.
PM: I come from an orthodox Madhva brahmin family. My grandfather Narayana Char was a lawyer practising in Anantapur. He had studied law in Madras and told me that, at that time, C. Rajagopalachari was a year or two senior to him in the law college. Most of my grandfather’s cousins too were lawyers.
My father Bheema Char studied and grew up in Anantapur. My father’s mother came from a place called Nagenahalli near the Bangalore area. For his B.Sc, my father moved to Machilipatnam, where he failed the first time. In fact, he always used to tell me that his father forced him to take up science, even though he didn’t want it. He was more interested in literature.
My father got married to my mother Saraswathi Bai who was also his cousin. He moved to Hyderabad, and tried to get a government job as a teacher in a high school. He did not get it for two reasons. One, he did not know Urdu and two, he did not satisfy domicile requirements. You had to be in Hyderabad for at least 10 years to get a government job there. So, he was a teacher in a private school when I was born. He thought it was a good idea to enrol me in an Urdu school so that I wouldn’t have the problems he had.
Before we go there, can you tell me about your place of birth?
PM: My birthplace is Hyderabad, and I was born on 3 November 1935.
What are some of your earliest memories from that time?
PM: The earliest memory I have is of my fifth birthday which was celebrated with a lot of women around me singing Devaranaamas2. I remember that we went to a photography studio, where they took a picture of me and my sister Uma.
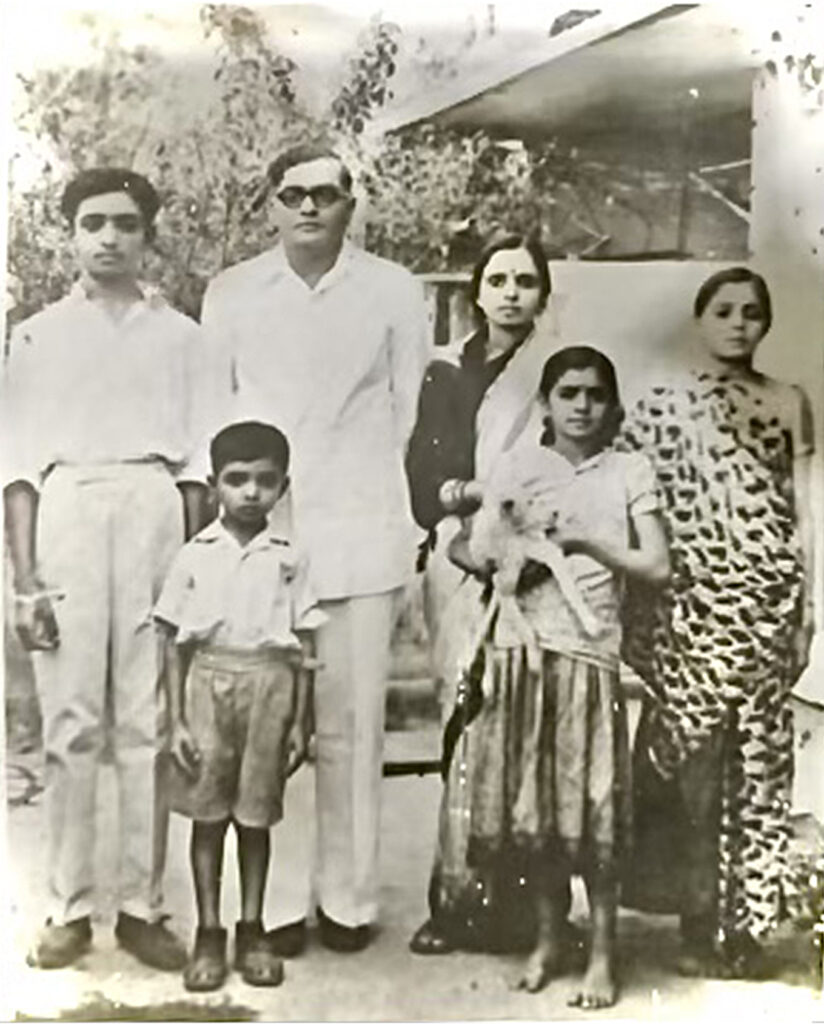
How many siblings do you have?
PM: We are four siblings. I have two sisters Usha and Uma and one brother, and I am the eldest among them. My brother Madhusudan, who was the youngest, passed away in 2015 and one of my sisters Uma passed away in 2022.
You were born in Hyderabad. Since you were Kannada Brahmins, do you remember any of your vacations to Karnataka?
PM: We used to go to Bangalore for vacation because my mother’s father is also from Bangalore. He came to Hyderabad for a job, and his father was also in Hyderabad before he went back to Bangalore after retirement. I remember that when I was two or three, my mother took me to her grandfather’s house in Bangalore for the Aksharaabhyaasa3 on rice. They made me write “OM” on rice with my hand.
Was most of your childhood spent in Hyderabad? Or did the family travel around? What was the language spoken at home?
PM: Aside from my vacations in Bangalore, my childhood was spent entirely in Hyderabad. One of the reasons is that my maternal grandmother was from Hyderabad. We spoke Kannada at home. Occasionally someone would burst into English, but generally, it was Kannada.
Until what age were you in Hyderabad?
PM: Until I went to the Tata Institute (TIFR) in 1958, when I was 22.
Do you remember the first school you went to?
PM: I went to several schools. I think one was called Pantulamma School, that was when I was four or five. There was a woman who used to run the place. I don’t have any memory of what I learnt there. The first memory I have is when I went to an Urdu school for two years, namely the third and fourth years, and I have good memories of that.
I remember you mentioning that your schooling was in Urdu medium, and you can easily talk mathematics in Urdu. How did this happen?
PM: I was put in an Urdu medium school maybe because my father could not get a government job, so he thought that it was good to learn Urdu. I don’t know how conscious a decision it was, but you know it must have been guided by the circumstances.
Were the blackboard lessons also conducted in Urdu script?
PM: Yes, of course. Everything was done in Urdu. I remember learning Euclidean geometry from an Urdu textbook that came from Punjab. I had no trouble studying in Urdu at all.
Was there a parallel grounding at home as well that exposed you to a whole view of things from that early time?
PM: My mother was deeply religious. So I started observing Ekadashi4 at the age of eight. My aunt, that is my mother’s sister, was just a year older, and she observed Ekadashi. I used to look up to her and even envied her. That was the kind of atmosphere I grew up in. I was glad because, after the observance of Ekadashi, they showered you with gifts.
I remember learning Euclidean geometry from an Urdu textbook that came from Punjab
I also remember you telling me that these were really demanding fasting sessions, and you used to have hallucinations.
PM: Yes. Even in the Hyderabadi summer, usually we used to go to my grandfather’s place for observing the Ekadashi, and he would say if we were feeling uneasy and so on, just place a wet towel on the stomach, and one would feel alright. That’s the best we could do.
But never intake anything.
PM: Oh no. Absolutely not.
So this is quite a radical situation at home. It is radical from a certain perspective but normal from some other perspective. How much of this would you attribute, as a contributing factor, to your robust physical constitution much later on?
PM: I don’t know. I don’t think in those terms at all. I don’t think I am so robust physically.
You used to run many marathons.
PM: So many people run marathons. Not everyone does Ekadashi (laughs).
Fine. When did you come to realize that you had a special liking for mathematics?
PM: I was reasonably good in school, and in high school, I started liking it because of a teacher by the name of Nasiruddin, who really encouraged doing trigonometry identities, factorising polynomials and such things in the ninth grade. I remember that sometimes he would ask me to come and do the problem on the board, all in Urdu. As I solved the problem, he would say: Did you really do it yourself? I would say “yes”. Then he would show a much simpler way of doing it, and say, “good you thought of some other way to do it”. He sort of encouraged me, so that was the first time that I developed a liking for the subject. It didn’t mean at all that I wanted to become a mathematician at that time. At home, everybody used to say that if one is good in mathematics, one should go to engineering, and if one was good in biology, then go to medicine; because that’s where the jobs were.
Was there any other subject that caught your fancy besides mathematics?
PM: Not so much in high school but once I came to college, that is the eleventh and twelfth standard, my whole life changed.
In what way?
PM: I met young students involved in the armed Telangana struggle,5 which was going on at that point. Some of the young people who had stopped going to high school got involved in it, even in the villages. Many of them were imprisoned and tortured. Finally, when the communist party—which was underground at that time—abandoned the armed struggle, some of them were released, and these guys were back to school. I met a friend who was in the same school for some time. He and I became very close and he introduced me to Marxism.
Once I came to college, that is the eleventh and twelfth standard, my whole life changed
So the Telangana struggle had a deep impact on your consciousness? What aspects of the Telangana struggle caught your imagination?
PM: It had the total support of the peasantry, so much so that Ravi Narayan Reddy had challenged Jawahar Lal Nehru to come to his constituency, and win. Even Nehru wouldn’t have won there. They had that kind of support. They started their own village committees and conducted meetings. They were even dispensing justice, and redistributing lands of some landlords, and they did all this with total support from the peasantry.
So would it be correct to say that the seeds for your radical politics, which were sown during the Telangana struggle, have continued to grow strong until today? For example, I see a lot of books by people like Noam Chomsky, Howard Zinn, Robert Fisk and, of course, Karl Marx.
PM: Yeah. We were part of the student union, most of whom were communists. I remember that I had put up a big poster of Stalin in my house. Somebody from college told my father that I was having all these friends who were talking about communism and so on, and that I shouldn’t be with them because I would not be able to get a job and so on. My father said “Remove that poster first”. I was still only a teenager then, and so there was already that rebellious stand. Of course, I had to remove it then, but after he left, I put it back again.
I remember that I had put up a big poster of Stalin
Is there a book or two that left an indelible impression on your young mind, both in politics and in mathematics?
PM: I read the Communist Manifesto and other books on Marxism during my first year of college. At that time, I also read a book called What is Socialism? by Ernest Mandel. Of course, by that time I was an atheist.
Anyway, I did mathematics, and I did well in it. Though at that time too, I was still not thinking of becoming a mathematician. In mathematics, I read a book by Schreier and Sperner on Matrix Theory.6 I couldn’t understand much of what they were doing at school, so I read it by myself, and I got interested.
Did you do mathematics with any particular friends of yours? Do you have fond memories of friends during those times?
PM: No. I used to just take a sheet of paper and do all the problems by myself, and just throw it away.
While the abiding interest in mathematics was always there, were you interested in other pursuits such as history, linguistics, music or sports?
PM: Not sports, except listening to cricket commentary. Music, of course, yes. I am not trained, but I like music in general. I used to listen to film music mostly, on the radio, and also ghazals7 because I knew Urdu. I could even understand what they said, and so on. I liked listening to Begum Akhtar. Sometimes I used to sing also. But my real interest in classical music, particularly Indian classical music, caught on after going to the Tata Institute.
What about your bachelor’s and master’s degrees? When and where did that happen?
PM: Everything in Hyderabad. It was called Osmania University at that time. My BA was in Mathematics, Statistics and Astronomy and I did very well, but I thought I didn’t do well, so on the very first or second day of joining for MA, I withdrew. And that was good for me because I spent the whole year reading mathematics books by myself. One of them was the book by Schreier and Sperner that I enjoyed very much.
When did you come to realize that mathematics is your true calling?
PM: Essentially after the MA in mathematics. I had to look for a job, and so after my BA, I actually went for a bank interview with the State Bank of India. I had to first take a written test. After passing the test, they gave me a free train ticket to Chennai for an interview. In the interview, I was asked “You are interested in mathematics, so who invented zero?”. At that time, I didn’t know. I said “Arabs”. “You may go now”, he said. I am happy that I was not selected. (Laughs)
So you entered TIFR to pursue your PhD in Mathematics in 1958. What was the experience at the entrance interview like?
PM: Well, I thought I had learnt some mathematics, but at the entrance interview, I was very nervous. First, they asked me, “So, you did some differential equations. What kind of differential equations?” I said, “Nonlinear differential equations”. “Of what order?”, one of them asked. I said, “Nonlinear differential equations.” “What order?” Again I said, “Nonlinear differential equations.” Then Balagangadharan said, “he is asking what order.” “Oh, first order”, I said (Laughs). Then they asked me what a continuous function is, and so on.

Do you remember who all were present on the interview committee?
PM: Yes, the interview committee had three people: K. Chandrasekharan, K.G. Ramanathan (KGR) and K. Balagangadharan.
So Balagangadharan was senior to you?
PM: Oh yes. Very much. He was much senior to C.S. Seshadri even. He was an extremely nice person. He knew a lot of Sanskrit and also had a very good sense of humour. He had all kinds of stories, and jokes, and was funny.
What topics in mathematics interested you when you joined the Tata Institute?
PM: I don’t know whether I had any specific interest but I attended all the first-year graduate courses. R. Sridharan taught topology I think, and Ramabhadran taught algebra. I think Balagangadharan taught analysis, measure theory and stuff. So, I went through that and of course, it was difficult for me. Actually, it’s very difficult for me to understand anything in lectures generally because my mind wanders. I don’t have a good attention span I think, and so I had to read afterwards. I knew what was going on, but I was not very good at following proofs and so on, in class.

Who were your batchmates?
PM: My batchmates were R.R. Simha, K. Ramachandra and Vasanti. At that time she was Vasanti Rao. I talked to her and then suddenly realised that she is related to me and that she was my mother’s cousin.

It is quite a coincidence that all four students were from Karnataka or Kannada speaking.
PM: Kannada speaking, yes. I was from Hyderabad.
Did you have close interactions with your batchmates?
PM: Oh yes. Particularly with Simha because we became roommates within a few months after I joined, and I was his roommate for seven or eight years afterwards.
Since I was at the Tata Institute much later, I have heard that during those days, as you were walking in the corridor, sometimes a senior mathematician would pull you into a room and interview you. Was this prevalent in your time?
PM: Not really. The only thing I remember is that I was once in the library and looking through the books in the old Yacht club. And, KGR comes along and asks me something like this: “Can you construct a field with 36 elements?”. But I don’t think there was ever any interview of the kind you mentioned.
One of my teachers in Hyderabad whom I admired, Mohammad Ahsan, had told me: “You know, when you go there, you will hear many things that you won’t understand. You shouldn’t pay too much attention to that kind of thing, and you should not get disheartened because you are not understanding something”, and this was quite true. When I went there, everybody was discussing mathematics at lunch and so on, which didn’t initially make any sense to me of course.
Mohammad Ahsan had studied at Aligarh University at the time when André Weil was there. He even had a gold medal, but for certain reasons, he initially went off into a job in agriculture. Later when he joined Osmania University, he was one guy I interacted a lot with. I used to go to his home and talk mathematics with him. He was like my mentor. I admired him because he was one who would try to do things rigorously. His wife is actress Shabana Azmi’s aunt, while actress Tabu is his granddaughter.

Nice trivia here. Later students of the Tata Institute, like Aravinda and I, have heard delightful accounts of your lively and uniquely playful personality, which would keep the general air of the campus upbeat and enjoyable. Especially so in an otherwise demanding life dedicated to studies and research. You have written some of your recollections of one of your batchmates K. Ramachandra.8 We would like to hear some of your own memories of life on the Old Yacht Club premises, and, later on, on the Navy Nagar campus.
PM: Well, the Old Yacht Club was a British club, and there were butler quarters which were later converted into hostels, and these were very dilapidated. It had lots of bed bugs, and rats too. We always wanted an iron cot so that we could light a match stick to kill the bed bugs. This was the atmosphere there, but even with all that, it was still quite enjoyable because of the company we had. In the Old Yacht Club, after breakfast, we would study till evening, and then come back to the hostel, and head for a walk. Again at night, we would go back to study, clad now in pyjamas, dhotis and so on. It was totally enjoyable.

Who were you interacting with mathematically, besides Simha?
PM: Besides Simha, the major interaction I had was with C.P. Ramanujam and Sridharan. C.P. Ramanujam would rarely come to the Institute when I joined in 1959. So I started going to his room, and thus got to know him better and better. I really enjoyed talking mathematics with him. I learnt quite a bit, so he was probably most influential for me.
What made it nice talking mathematics with him?
PM: It was easy to talk to him. He was very mild-mannered. We also interacted socially and used to go to movies and do many things together. And when we moved to Navy Nagar, we were roommates there in the office. So I was Simha’s roommate in the hostel and Ramanujam’s roommate in the office.
So he had an impact on your early mathematical life. Can you tell us what you learnt from him?
PM: We used to discuss algebra and basic algebraic geometry, and then in fact we started a seminar on differential equations, but it sort of fizzled out after two or three sessions.
I also noticed that your first paper listed on MathSciNet is in The Mathematics Student. It’s about differential equations. Did Ramanujam have any influence on that? It was published around 1961, I think.
PM: No. It was written before I came to the Tata Institute.
Before this paper, I had also sent another one to The Mathematics Student. If you look at it, it is pretty embarrassing now, but it was something about a new proof for the rank of the product of two matrices. I mean, that was my level of mathematical maturity before I came to the Tata Institute!
When did your interest turn more algebraic?
PM: Somehow, I felt that I didn’t know analysis very well, and also algebra looked more approachable. So, I studied algebra and then I started studying algebraic geometry, reading books by Solomon Lefschetz Algebraic Geometry and Serge Lang Introduction to Algebraic Geometry. I also read some parts of André Weil’s Foundations of Algebraic Geometry but never got beyond the first couple of chapters.
When did your mathematical relationship and friendship with Seshadri start and what was his influence on you in the early years?
PM: In my early years at TIFR, Seshadri was in Paris and I was waiting for his return because Ramabhadran had suggested that I might become his student. I met Seshadri when he came back. He had attended Alexander Grothendieck’s seminars on the EGA (Éléments de Géométrie Algébrique).9

Seshadri started a seminar on EGA, starting with schemes, products of schemes and the commutative algebra we needed to know. He had also attended Jean-Pierre Serre’s lectures, from which later came out the book Algèbre Locale. He had the handwritten notes. He gave it to me and said, “you read this and lecture once or twice a week”. We used to talk about EGA and I lectured about once a week on Commutative Algebra by Serre. This book hadn’t yet come out. That was, of course, a big influence on me.
Coming to your thesis, who suggested the topic?
PM: Seshadri suggested studying vector bundles over the product of an affine line and a curve, possibly singular.
Great. So what was your thesis topic about?
PM: Seshadri had proved that if you take the product of a smooth affine curve with a line, then every vector bundle comes from the curve. I generalized this to the product of an arbitrary curve and a line. The proof was an adaptation of Seshadri’s original proof.
Then one sees a branching out in your work to more non-linear considerations like commutative algebra and so on. But I want to first talk about your work with Hyman Bass on the Whitehead group of finitely generated abelian groups if I am not mistaken.
PM: Before Hyman Bass came to TIFR, we had started studying algebraic K-theory because when Harish-Chandra came to the Tata Institute on a visit, he made us aware of this paper K-theory and stable algebra by Bass. I wrote to Bass and he sent me his paper in the Publications mathématiques de l’IHÉS.
Sridharan and I, and a few colleagues, started reading it. Then when Bass visited TIFR, he introduced me to the following question of Milnor: are Whitehead groups of a finitely generated Abelian group finitely generated?
Did this have some topological or geometric motivation?
PM: Yes. But my interest was purely algebraic.
What year was this?
PM: By that time, I had written my thesis and so it must be 1965–1966.
Because Amit Roy wrote his Lectures on topics in algebraic K-theory. It was there at the same time.

PM: Yes. Bass was giving that course.
Indeed. In fact, Bass comments that Amit Roy’s writing is so beautiful, and has added much more value to the exposition than what he himself lectured on. In some sense, Bass was your mentor too, right?
PM: Bass and Seshadri were my thesis examiners, and they were also certainly my mentors. My thesis was about the splitting of projective modules over the polynomial ring over a one-dimensional Noetherian ring (with mild hypothesis). In view of this, Bass suggested that I should try to show that the K_0 of the integral group ring of a rank one finitely generated abelian group is finitely generated. This would be true if Milnor’s question had an affirmative answer.
I found a counterexample by showing that the K_0 of the integral group ring of G=\mathbb{Z} \times \mathbb{Z} / p^2 (for prime p) is not finitely generated. This was the starting point of my collaboration with Bass.
Then you had this paper in the Annals of Mathematics which was about vector bundles over affine surfaces birationally equivalent to a ruled surface. This was around 1969. How did that come about?
PM: The result in the paper you mention easily follows from the observation that Seshadri’s algebraic proof of the triviality of vector bundles over an affine plane has the following geometric interpretation: vector bundles over a smooth affine surface with lots of smooth rational curves split into a direct sum of a trivial bundle and a line bundle.
 |
 Chennai Mathematical Institute |
Very nice. I also noticed that there is a certain connection with Bass. It’s not about modules, but concerns rings. You have this beautiful theorem which is a converse of a result of Bass. Namely, if R is an image of a regular local ring which is a unique factorization domain, then it is Cohen–Macaulay if and only if it is Gorenstein. How did this come about?
PM: This came about because I learned about Gorenstein rings when Pierre Samuel came to the Tata Institute. A question which Samuel asked was whether unique factorisation domains are Gorenstein. I didn’t know much about Gorenstein rings initially, but fortunately, I knew Grothendieck’s way of thinking about Gorenstein rings in terms of Ext groups. The canonical divisor can be expressed in terms of the Ext group. I could prove that if a quotient of a regular local ring is factorial and Cohen–Macaulay, then it is Gorenstein.

Being from Brandeis University, I am curious to know if you had any interactions with Maurice Auslander and David Buchsbaum.
PM: Yes, I knew Auslander, but not Buchsbaum in the beginning. That’s because I was reading a paper by Auslander on unramified regular local rings. In this paper, he shows that if any Tor group vanishes, then all the higher Tor groups vanish. I showed that for any regular local ring, if two consecutive Tors vanish, then all higher Tors vanish. A later result of Lichhtenbaum supersedes all these results.
Kind of rigidity of Tor.
PM: Yes. Then Auslander had some questions about `depth’, and I found an easy counter-example.
This is the Illinois Journal of Mathematics paper on modules over local rings. It is quoted as recently as 2021 by young mathematicians. There still remains an abiding interest in these kinds of questions. Did you also know my thesis advisor David Eisenbud back then?
PM: Yes. I first met him in Oberwolfach in 1970, if I remember the year right. Then I used to meet him at conferences and we enjoyed talking mathematics together.

You have had many colleagues during long years of your academic life stretching to well over 60 years. The longest association you have had has been with Raghavan Narasimhan, and it has been a special friendship. There are many legendary stories about Narasimhan at the Tata Institute. Can you talk about Narasimhan and others whom you have come across in your career?
PM: Sure. I knew Narasimhan from the day I joined the Tata Institute. He was very very nice to me. There was a lawn of the Old Yacht Club where we used to sit and talk often in the evenings, and on many of those occasions, we used to go out for dinners. I was his neighbour in the dorm. So we used to meet early in the morning as well.
I was also very close to C.P. Ramanujam. He and Narasimhan had studied together in college before they both joined TIFR. I didn’t see Narasimhan as often as I saw Ramanujam then, but after I came to Columbia University, Narasimhan and Raghunathan, who were visiting the IAS (Institute for Advanced Study) in Princeton, used to come to New York almost every week; and I used to visit them in Princeton. So we met often and our friendship grew in time steadily.
Once I came to Chicago, my friendship with Narasimhan became even more cemented. I have a great admiration for his mathematics. His interest in wine, and whatever he did, was done with such passion that it was quite admirable. He was a kind person who helped me a lot, and if I had any problem, I used to go to him first. We used to discuss mathematics quite a bit. In fact, whenever I had questions about affine varieties, I used to ask Narasimhan if answers were known in the case of Stein manifolds. If I did something in mathematics, I would tell Narasimhan first.
With Seshadri also, I had a very close relationship, and our families too had a close bonding.

Tell me about your collaboration with Mohan.
PM: I first met Mohan Kumar when I was in Delhi in 1978-79. Our collaboration really began when I returned to the University of Chicago during his second year as a Dickson Instructor there, and strengthened when we were both in Mumbai in 1981-83. Upon my arriving in Mumbai in 1981, Mohan and I started thinking about the following problem: Let V be a smooth n-dimensional affine variety. Let P be a vector bundle of rank n. Suppose the top Chern class (with values in the Chow group of zero cycles) vanishes. Then P splits off a trivial bundle of rank one. Mohan and I had a breakthrough by proving this statement when V is of dimension 3. A major contribution came from Mohan’s work in his Commentarii Mathematici Helvetici paper in 1984.10 Finally, the problem was solved in the general case in my paper in the Annals of Mathematics in 1994. In a true sense, this work was the result of a joint effort of Mohan and myself.
You left the Tata Institute around 1970. Could you recall a bit about your life around that time?
PM: I formally left TIFR on November 25, 1970. Before that, after spending a year as a postdoc at Columbia, I had a visiting position in 1967–68 at the University of Illinois at Chicago. When I was there, I used to attend algebra seminars at the University of Chicago run by Kaplansky. He and I used to discuss mathematics and he asked me to speak in his seminar. At the end of that year, Kaplansky asked me if I would be interested in a permanent position at the University of Chicago. I told him that I was interested, but that I was committed to staying at TIFR for two years. After a year, I got a letter from Narasimhan stating that the University of Chicago would like to offer me a job. So that’s how I ended up being in Chicago.

I had made up my mind to leave for various reasons, including the delicate health of my wife Prema. So, I had already accepted the University of Chicago offer at that time, but I did not have a visa. Therefore I spent a year at the Forschungsinstitut für Mathematik in Zürich, before moving to Chicago in 1971.
So you had a long innings in Chicago until your retirement.
PM: I retired in 2006, but until 2015 I was giving a course every year.
Let’s go back a little. Can you tell us about your efforts to prove Serre’s conjecture? What prevented you from proving it for the general case?
PM: I was only thinking about Serre’s question for three variables. Using Abhyankar’s construction of three explicit generators for a smooth curve in affine 3-space, I essentially reduced Serre’s question to a result which Jacob Towber had orally communicated to me in 1967. Thus, in 1973 I contacted Towber and we collaborated to finish the proof. I remember Towber telling me that for him it was like he had put his result in the bank for several years and then collected dividends!
 |
 |
Apart from mathematics, what are the other things that have held your continued interest? I know about your radical politics. You participate in meetings and sign petitions. Can you expand on that?
PM: Originally, my interest in these matters started when I was 17 or 18. Nowadays, I am actually trying to read more about how capitalism works. I recently finished reading Das Kapital, and I am trying to read some other writings of Marx.
As I understand, Marx has left a deep impact on your conscience.
PM: You are 100% right.
What exactly is it about him and his political philosophy that moves you?
PM: From the beginning, even though I didn’t understand it this well back then, the whole materialistic approach, historically, posits that matter exists outside human consciousness.
It was so easy for me to see that point. Also, his simple way to express how profit or surplus value is created, and in the whole of human history how human labour is so important. These are some of the things which I am reading more about nowadays, and spending much more time on. I have vague ideas, but I am trying to clear up my thinking now. My son Viren is of much help to me in this.
 |
 |
You also run marathons. You have done it for many years and are very motivated. It is a physically demanding pursuit. You once told me that when you are doing a marathon, it’s like meditation. Do you have any thoughts to share on that?
PM: There is not much to talk about. The way it started was that my son Niren wanted to run, and he said, “Why don’t you come with me?” So I ran with him for a few days, several days in fact, and then afterwards he stopped, but I continued. I could see that I could run two miles, three miles, and so on. Then I started reading about how to train myself. I enjoyed the loneliness of a long-distance runner (laughs). There is even a book called The Loneliness of the Long-Distance Runner.11 So it’s quite interesting that the mind goes through many changes during the long run. It is in that sense meditative, I agree.
Getting back to some mathematics, you have witnessed a lot of change in the mode of publishing research findings these days. Also, collaborations have become more common compared to the time you started as a PhD student. What personal impressions do you carry about publishing, changes in the mode of publishing research, and such? Would you say that pressure on younger people is much more these days?
PM: Yes certainly. The way capitalism has evolved, young people are now feeling its effects. I read in the New York Times the other day that many young people realize that their parents around the same age, already had a job, enough money to buy a house, marry and have children; but many of the current generation are struggling and still single. Obviously, this is going to penetrate into the academic world too. I see that it is much harder now.
All these universities themselves have turned out somewhat like corporations, and so many people have even been denied tenure for political reasons.
And hiring far more adjunct professors, so that they don’t possibly have financial bindings perhaps?
PM: Oh yes. I agree.
Do you see all of these patterns emerging, when you read Marx? Do you see that he predicts these kinds of things?
PM: Yes. Some of it. Marx mainly wrote about working people and that includes academics, but that was not his main focus. He himself could not secure an academic job because of his views and writings. He was driven out of Germany and then of France and eventually lived in London. He was always poor; the only money he earned was as a correspondent for the New York Tribune. Friedrich Engels helped him some, but Marx could not even save his own son, who died because Marx could not buy the prescribed medicines.
I enjoyed the loneliness of a long-distance runner
Let me rewind back a little. Were you at the Tata Institute when the International Colloquium happened there in 1966, in which Grothendieck participated?
PM: No. I was in Chicago at that time, at the University of Illinois at Chicago. But I heard about it from S.S. Abhyankar.
I guess Abhyankar and you were good friends?
PM: Yes. He was very happy that Towber and I proved the Serre conjecture for three variables using his work.
What was your experience writing lecture notes for Samuel’s lectures on unique factorisation domains?
PM: Oh, it was very pleasant. I used to meet with him regularly when the notes were being written.

Tell me about your interaction with Samuel. He too was into radical politics, and so did you ever talk politics with him?
PM: No. I came to know about his political interests only later. He was strongly against the use of nuclear weapons.
But you had quite a bit of interaction with Samuel?
PM: Yes. I even went to his retirement conference. The paper with Bloch and Szpiro “Zero cycles and number of generators of an ideal” was written for that conference. Samuel was a very kind and generous person, and very helpful to me.
You have had a number of mathematical influences, as I understand. Can you please name them?
PM: I have been around for such a long time, naturally I came into contact with many mathematicians and their ideas. Besides the people whom I have already mentioned, here are some of the other people who had a mathematical impact on me.
Of course in Chicago, Madhav Nori has been a close friend and colleague for many years. In all these years, our many mathematical conversations have deepened my understanding and enjoyment of mathematics. I had numerous conversations that led to collaborations with R. Swan, S. Bloch, L. Szpiro, and M. Kervaire. Others who had an impact on my mathematics were V. Srinivas, M. Ojanguren, Ravi Rao, A. Roy, S. Mandal, S.M. Bhatwadekar, Raja Sridharan, and D. Mumford. Of course, this list is incomplete.
Do you still think about mathematics these days?
PM: Not very much really. I try to think about some problems but I need some ideas. I don’t have any right now (laughs). I don’t generally think much but just to say for example, is the embedding of A^2 in A^5 a complete intersection? Even that is not known, so sometimes I just like to think but I don’t go very far. Then I pause a bit and go back to my reading of Marx.
There is one question that has come to our mind that we want to ask. While you are very passionate and involved, as we understand, regarding politics and injustice in systems, communism, capitalism and such, you are quite detached from the sociological aspects of it when it comes to the world of academics: a quality that some of us have noticed present in you to an unusual degree, and which is not usually seen in the academic world. What do you attribute this detachment to?

PM: No. I am not really detached but I look at it from a global point of view, so to speak. There are many serious things going on in the world that you could be doing rather than getting into sociological aspects of the academic world. You know it’s there, but it’s all part of the system. Much more serious injustice and corruption exist in the world. This is how I look at it. I don’t agree with you regarding the use of the word detachment. All I am saying is that there are so many things going on in the world, and mathematics is one of the many things out there. It is nicely encapsulated in this Urdu poetry, by a famous Pakistani poet Faiz Ahmad Faiz. He says
Aur bhī dukh haiñ zamāne meñ mohabbat ke sivā
Rāhateñ aur bhī haiñ vasl kī rāhat ke sivā
which means: There are other sufferings of the time besides love. There are other joys, besides the joy of the union. I think it sounds much better in Urdu.
Beautiful
PM: Faiz was a very famous Urdu poet, who was for some time held in jail in Pakistan. He was a Marxist, and I think one of the best poets in the world.
Very philosophical and spiritual, and Marxist. I want to ask you how what you recited is relevant to the question that I asked.
PM: In a sense, what you call detached, in reality, is actually attached. I am attached to several things in my mind. So, that’s the reason I said I look at it all from a global point of view. The gist of this poem is, in essence, captured by the two lines I recalled just now, and the poem’s beginning line `Do not ask me now, beloved, for that love of other days’.
I am attached to several things in my mind
Now I will recite to you the whole poem. I am going to torture you (laughs). Here is the poem:12
Mujh se pahlī sī mohabbat mirī mehbūb na maañg
Maiñ ne samjhā tha ki tū hai to daraḳhshāñ hai hayāt
Terā ġham hai to ġham-e-dahr kā jhagḍā kyā hai?
Terī sūrat se hai aalam meñ bahāroñ ko sabāt,
Terī āñkhoñ ke sivā duniyā meñ rakkhā kyā hai?
Tū jo mil jaa.e to taqdīr nigūñ ho jaa.e
Yuuñ na thā maiñ-ne faqat chāhā thā yuuñ ho jaa.e
Aur bhī dukh haiñ zamāne meñ mohabbat ke sivā
Rāhateñ aur bhī haiñ vasl kī rāhat ke sivā
An-ginat sadiyoñ ke tārīk bahīmāna tilism
Resham-o-atlas-o-kamḳhāb meñ bunvā.e hue
Jā-ba-jā bikte hue kūcha-o-bāzār meñ jism
Ḳhaak meñ luthḍe hue ḳhuun meñ nahlā.e hue
Jism nikle hue amrāz ke tannūroñ se
Piip bahtī huī galte hue nāsūroñ se
Lauṭ jātī hai udhar ko bhī nazar kyā kiije?
Ab bhī dilkash hai tirā husn magar kyā kiije?
Aur bhī dukh haiñ zamāne meñ mohabbat ke sivā
Rāhateñ aur bhī haiñ vasl kī rāhat ke sivā
Mujh se pahlī sī mohabbat mirī mehbūb na maañg
I could feel the import of the poem in your lively expression as you read it. And it appears to me that the poem also captures your own philosophy of life and attitude towards mathematics and academics. It was truly delightful.
Thanks a lot, Pavaman. You have been an influential person to many younger people including me. I deeply thank you for taking the time and talking to us about your life and experiences inside and outside the academic world. \blacksquare
Acknowledgment We are immensely grateful to Lynn Narasimhan for her kind and generous help at every stage of preparation and editing of this article. We also record our deep gratitude to Shilpa Gondhali for her ever willing help in transcribing the interview from the audio recordings.
Footnotes
- A residential complex in the TIFR housing colony right opposite the institute campus in Colaba in Mumbai. ↩
- Interpreted quite literally, a `Devaranaama’ invokes the name of a God. These are verses and hymns in praise of the divine and are present in various forms, metres, and languages in all parts of India. The nomenclature `Devaranaama’ is predominant in Kannada. ↩
- `Aksharaabhyaasa’ is a compound word in Sanskrit consisting of two words `Akshara’ and `Abhyaasa’. The first word is literally and symbolically a letter of the alphabet and serves as a metaphor for knowledge. `Abhyaasa’, refers to a sustained practice. In an extended context, the compound word means the pursuit, practice and a lifelong quest for knowledge. Typically young kids are led through such initiation rites, where family elders hand-hold them, and guide little fingers to trace the sacred symbol `OM’, on a plate usually filled with rice or other grains. ↩
- `Ekadashi’ is the eleventh day of the Hindu calendar, and is considered particularly sacred. Many communities observe a fast on this day and refrain from eating and drinking the entire day, while choosing to spend the day in prayers and learning. ↩
- The Telangana Rebellion (1946–51) was an armed revolt of peasants led by the communist party of India. ↩
- Introduction to Modern Algebra and Matrix Theory by O. Schreier and E. Sperner, Second Edition, translated by Martin Davis and Melvin Hausner; originally published in 1951 by Chelsea Publishing Company, New York. ↩
- Originating in the Middle East, a Ghazal is an ode or a poem that talks of emotions related to various aspects of love. Though Arabic in origin, it is now a popular component of South Asian poetic traditions, where patrons typically congregate in `mehfils’ to enjoy Ghazals, composed largely in Urdu. ↩
- See K. Ramachandra: Reminiscences of his friends, Hardy-Ramanujan Journal, Vol. 34 & 35, (2013) 53–63. https://hrj.episciences.org/177/pdf. ↩
- The Éléments de géométrie algébrique (Elements of Algebraic Geometry) by Alexander Grothendieck (assisted by Jean Dieudonné), or EGA for short, is a rigorous treatise, in French, on algebraic geometry that was published (in eight parts or fascicles) from 1960 through 1967 by the Institut des Hautes Études Scientifiques. In it, Grothendieck established systematic foundations of algebraic geometry, building upon the concept of schemes, which he defined. The work is now considered the foundation stone and basic reference of modern algebraic geometry. ↩
- Comment. Math. Helv. 59 (1984), 243-252. ↩
- Loneliness of the Long-Distance Runner by Alan Sillitoe, Published by Macmillan, 1968. ↩
- For a translation into English by Victor G. Kierner, please follow this link http://www.columbia.edu/itc/mealac/pritchett/00urdu/3mod/kiernan_faiz/06_lovedonot.pdf. ↩
