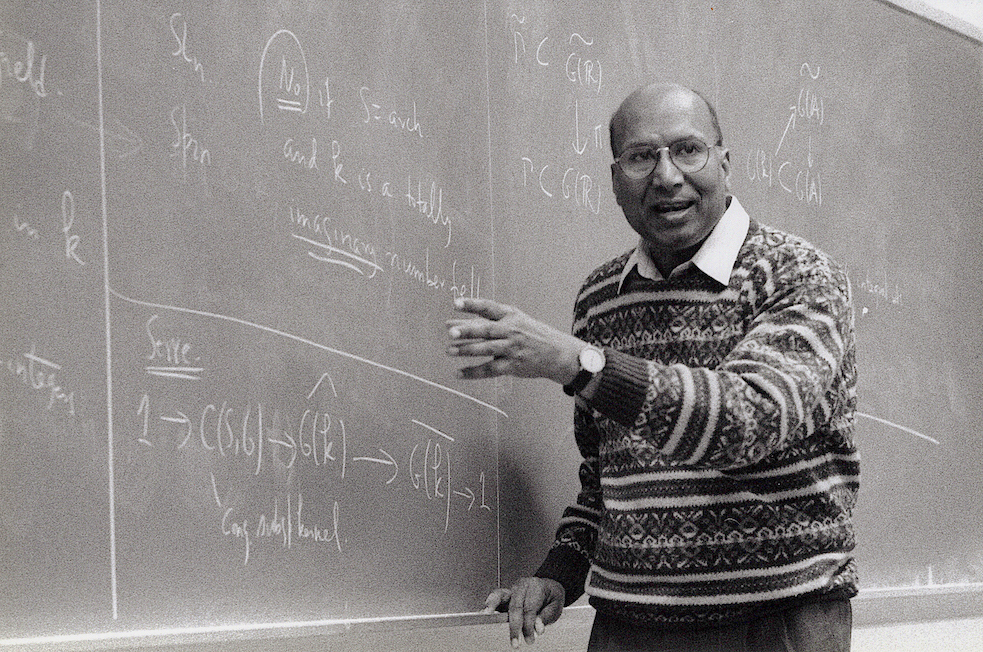
Going through the grind of generally uninspiring school and college years, but propelled by a series of subconscious decisions at crucial turning points landed him in the exciting company of some of the most distinguished players in mathematics. A six-time long-term visiting member of the famed Institute for Advanced Study in Princeton, Gopal Prasad has an enviable record of highly impactful research publications in some of the most prestigious forums in mathematics. Acquiring an unquestionable expertise in the esoteric topic of Bruhat–Tits theory, Gopal Prasad’s insightful foray into the topic resulted in a new approach to the field. Celebrating his unique success story in a most befitting manner, his son and daughter have endowed the Gopal Prasad Professorship in April 2022 at his favourite destination – the IAS, Princeton.
The Bhāvanā team spent an entire day with the Gopal Prasad and Indu Devi couple, and engaged in a fascinating conversation during their recent visit to the International Centre for Theoretical Sciences in the city of Bengaluru. The following interview article captures the highlights of the invaluable time spent in their warm and friendly company.
Dear Professor Gopal Prasad, thank you for speaking to us! It is an immense pleasure and honour for us to talk to you.
GP: Thank you for the initiative you have taken. I am really greatly honoured by your invitation to speak to the Bhāvanā team and I will be very happy to see the result.
You have been a great support to Bhāvanā. It means a lot. Starting from the beginning, can you please recall memories of your childhood, your parents, and also your family background?
GP: I grew up in a business family in Ghazipur, Uttar Pradesh. Before I went off to do mathematics, the family was engaged purely in business. We are a Marwari family who moved from Charkhi Dadri (in Haryana) to Ghazipur around 1850, with little money. Some of my ancestors later moved to Buxar (in Bihar). Both Ghazipur and Buxar are on the banks of the river Ganga. Buxar is located to the east of Ghazipur. My father was born there, but after a while, he moved to Ghazipur. My father’s Bhabhi (an elder cousin’s wife) lost her husband soon after her marriage, so she adopted my father who was a toddler at that time, as her son. My father always treated her as his mother, though his biological mother (who was born in Karachi and passed away in 1965) also lived in the same house in Ghazipur. He always treated and respected both of them equally well. I was quite close to both grandmothers. They were very affectionate with me and all of my siblings.
I had seven brothers and three sisters. It was mostly my grandmother who raised us all. She was extremely loving and caring. She had only a primary school education, but she regularly read Hindu mythology, religious books and newspapers.
Could you tell us their names and what they did?
GP: My grandmother’s name was Anardeyi Devi, my father was Ramkrishna Prasad and his brother’s name was Govind Prasad. My mother, Lakshmi Devi, was born in Varanasi which is 75 Km from Ghazipur. Both my parents were gifted with considerable native intelligence. Many Marwari families moved from Rajasthan and Haryana in the nineteenth century, to escape adverse conditions, to UP [Uttar Pradesh], Bihar, Bengal and some even as far south as Chennai. They were very hard-working and enterprising. They established and acquired many industries, businesses, and some well-known newspapers (Hindustan Times, Indian Express, and Times of India are some of these).

One of the first flour mills in Kolkata was founded by my ancestors. They also had an insurance business. Before the Railways came, freight was moved and people travelled by river, by rowboats and/or big barges. All freight transport from Allahabad1 to Kolkata was by these boats. They would transport vegetables, grains, sugar and fish. One might be surprised that transport insurance existed 150 years ago in North India. My ancestors were insuring boats at that time.
That region of UP and Bihar was very famous for khaṇḍsārī sugar, a type of unrefined sugar which is slightly brownish. My family was also engaged in the sugar trade. Later, they got into the business of coal mining. They leased a coal mine in Bengal from the local Maharaja. A British company, Andrew Yule & Co, was given the contract to mine the coal and the family received a monthly royalty. This passive income in a way spoiled them. The family eventually lost the lease, and internal conflicts resulted in a major division within the family. Then some parts of the family moved to Delhi, Kolkata and Hathras, but my parents, grandmother, great-grandmother, and my father’s biological parents stayed on in Ghazipur.
By the 1930s the family was not in a good shape financially, having lost the coal mine lease and closure of other businesses. My father’s biological father, Madanmohan Prasad, was a travelling salesman in the sense that he would travel to towns near Ghazipur, and take orders from cloth merchants for cloth mills earning a commission. But he did not earn much.
So your father started a new business?
GP: Yes, my father and his elder brother Govind Prasad started a business in partnership from very modest beginnings. In 1937, they established Prasad & Co. dealing with bicycles and Usha sewing machines. In those days, bicycles were imported as there were no locally produced bicycles. Even after Independence, we used to get import licences from the Reserve Bank. I remember that at least until the 1950s, though local production had started, we still relied on supplies from abroad, especially for popular brands such as BSA, Raleigh, and Hercules. We also imported sewing machines at that time. There used to be a popular German sewing machine company by the name of PFAFF. My father told me that during the Second World War, when the PFAFF consignment came, it also came with translated copies of Hitler’s autobiography Mein Kampf as propaganda material.

My father was also quite active in the freedom movement, but never sought any elected office after independence. He would welcome and provide support to the Congress leaders passing through Ghazipur. I remember having a banner which was prepared to welcome Netaji Subhash Chandra Bose, with the message, “The great revolutionary Subhash Chandra Bose is welcome’’, written in Hindi. In 1942, during the Quit India movement, my father was imprisoned for a year and sent to Banaras Central Jail. Many freedom fighters were rounded up at that time from various places and confined in different prisons. For example, Nehru was confined in Naini prison near Allahabad. They were treated well because they were political prisoners. They were not handcuffed, and inside the prisons, they were essentially left free. My father told many interesting stories about his days in jail. They could get magazines and books. My father told me that he did quite a bit of reading in jail because he had nothing else to do. I have several of his books which he acquired during that time.
During my father’s imprisonment, most of the family stores were closed down as they couldn’t be taken care of. The business shrank to just one or two stores until they opened branches in Kanpur, Arrah (in Bihar), and Deoria (near Gorakhpur, UP).
Even after his release from jail, my father continued to be involved in the freedom movement. During Indira Gandhi’s regime, those imprisoned during the freedom movement were given copper medals (tāmra-patra) and a railway pass to travel for free in second-class AC with a companion. He availed this when he and my mother used to come to stay with us in Mumbai.
So he had some conviction, to not seek political offices…
GP: Yes; but he was very interested in the upliftment of society. He was involved in establishing the first undergraduate degree college, which now also offers post-graduate education, in Ghazipur. He was also involved in establishing a Degree college for girls. And then, he established a Homoeopathy college. He was involved with the leprosy eradication programme of the Government of India.
Are you the eldest of your siblings? We know that two of them, Shrawan Kumar and Dipendra Prasad, are mathematicians like yourself, and a third one, Pawan Kumar is an astrophysicist, which reflects a strong presence of academic excellence running in the family. Was there a special emphasis at home to do well in academics?
GP: I am the second eldest of eleven children. We studied in very ordinary government schools. During my primary school, I sat on the floor on a strip of cloth like a runner, and we wrote on painted wooden planks with chalk. I was enrolled in a school in the third grade. I didn’t go to school earlier, since the nearest primary school was somewhat far from my home. We had a tutor who came home to teach children. I really liked my first tutor. During my visits to Ghazipur from Mumbai I would often visit him.
My elder brother Rajendra Prasad, who unfortunately passed away in 2015, joined the business. Later, one of my younger brothers, Shyam Sundar Prasad, also joined the business. But still, my father expected me too to join the family business after my BSc since in my family no one ever did anything else. So after my Intermediate (that is 12th grade), he sent me to Arrah as an apprentice to my brother who had a store there and also to continue my education. After my BSc (Hons), even though I had topped in Magadh University (to which my college, Harprasad Das Jain College, was affiliated), my father asked me to join the family business. I was very sad about this decision, so my grandmother (Anardeyi Devi) intervened on my behalf and persuaded my father to change his decision and then he relented. I am indebted to my grandmother that I was able to go for my Masters and after that eventually join TIFR and continue in my mathematical career.

After I was invited by Yale University in 1972, before earning a PhD, my father felt that pursuing a career in science and mathematics was pretty good. So three of my younger siblings: Shrawan, Pawan and Dipendra were encouraged to go for higher education. He sent Shrawan in 1973 for an MSc in mathematics at Bombay University, and later in 1975 Pawan and Dipendra for further education in Mumbai. Dipendra joined St. Xavier’s college for a BSc, and I suggested Pawan to join IIT Kanpur, which he did, and obtained a Masters in physics and M. Tech in computer science there. After I returned from the US in 1974, Shrawan moved with us to Bhaskara (in TIFR Housing Colony) and lived with us till his marriage. Dipendra also lived with us while in BSc. After completing his BSc, he went to IIT Kanpur, where he earned MSc in Physics.
Indu and I are extremely happy that my three younger brothers did not have to persuade our father to continue their higher education; on the contrary, they were encouraged and supported to follow their passion. All three have done extremely well in their fields. This makes us very proud.
Did you enjoy your early education? Are there any particular anecdotes you may have?
GP: My primary school was about a kilometre from home, and there were no bathrooms in it. In fact, most schools didn’t have bathrooms in those days (this was soon after India gained independence). Maybe just as well given the lack of bathrooms, you couldn’t drink water there the entire day as there was no running water in those schools and there was no tradition of carrying water from home. So at the end of the day, the children raced home to use the restroom. My memory of those schools is not so fond and my memory of my teachers in primary school is almost nil. But I did learn to read, write and do some basic arithmetic and memorize the multiplication tables.
Teaching would happen in Hindi, I suppose?
GP: Yes. All communication was in Hindi. The teaching of English began in sixth grade. It was quite minimal, there was no exposure to spoken English. I couldn’t speak fluently. I started to speak English only when I went to TIFR after my masters. My father could speak a little English because he had studied up to ninth grade. You know, in those days of British rule, teaching of English was quite good. He could write business letters and also knew how to type. He asked me to learn typing and sent me to a typing school, because in business correspondence it is a skill that is good to have. But I did not pay much attention to it, so I never learned how to type well. We had several typewriters at home, and we had a clerk who would type letters that my father dictated to him.
What are the names of places, courses you attended and degrees you earned before you joined your research programme?
GP: I completed sixth grade in 1954 in Dayanand Anglo Vedic (DAV) Inter College, a school in Ghazipur near my house. Though I passed the exam, I do not think that I was inspired much academically in that school. Back then, I had no interest in languages, history, geography and humanities.
For my seventh grade I went to the Marwari Inter College in Kanpur, where there was a branch of Prasad & Co. looked after by my father’s elder brother. As this store suffered big losses in the hire-purchase scheme,3 it was decided to close the business. My father went there in 1954 for a year, to help recover the losses and close the store.
My seventh grade was not good because I used to get a lot of headaches at that time, and I had to leave Kanpur before completing the school year. I didn’t like living in Kanpur. Even though it was an upper middle-class home, bathrooms were shared. This caused a lot of inconvenience.
After leaving Kanpur in 1955, I went to spend some time with my mother’s sister in Varanasi. I spent a month or two there recuperating from my headaches. And in fact, miraculously, I became better. I moved back to Ghazipur, as did my father after he closed the Kanpur store. I was admitted to a junior high school to repeat my seventh grade.
When did your serious interest in mathematics begin? Was it during your school or college years?
GP: My only memory of this school is that I got interested in mathematics. Counterintuitively, my reason for becoming interested in mathematics is that my teacher had a poor understanding of plane geometry and wanted us to memorize the proofs, which led me to study independently and come to appreciate the topic well. Providing proofs did not appear difficult at all, and I did not need to memorize them. My interest in mathematics began then in seventh grade through geometry.
From ninth grade onwards, my teachers were generally good. My memory of my maths teacher, in the 11th and 12th grades, is especially good. A new maths teacher, Vijay Shankar Pandey, joined the school. He had recently finished his MSc in maths. He was a very good and encouraging teacher, and we learnt some algebra, trigonometry, dynamics and differential calculus. He liked me because I was doing well in my studies, and he really encouraged me.
I really loved collecting exercises from various books during my high school, studying topics like permutations and combinations, and became totally immersed in mathematics. I was also interested in physics and chemistry and did quite well. But in the chemistry lab, I had trouble: many experiments involved detecting colours or colour changes, like titration, in which a solution turns from acid to base drop by drop. I didn’t realise that my problem was colour blindness. I just thought that I was bad at experimentation. My colour blindness was only detected much later by Dr Jotwani (the resident TIFR doctor) in 1966 after my selection in TIFR.
In the undergraduate college (Harprasad Das Jain College, in Arrah), I chose maths for my “Honours’’. In Bihar and Bengal, Honours meant that you learned much more in your chosen subject than in the ordinary BSc. My maths teachers were quite good, and they liked me. We used some very good books in honours classes.
Which university granted your BSc Honours degree?
GP: Magadh University, to which my college was affiliated. Its headquarters are in Bodh Gaya, where Buddha got his enlightenment.
Was that when you decided to take up mathematics as a career option?
GP: I topped in BSc (Hons) at Magadh University. But to my father, this did not matter much. He was a real businessman and it was enough for him that I passed.
So after my BSc came the crucial question, of whether I would be allowed to study further. As I narrated earlier, due to my grandmother’s intervention my father reluctantly permitted me to study further.
Indu PrasadShe deserved great respect. She only had a primary education, but she championed education. She would read a Hindi newspaper every day, unusual for a woman in her community in those days. All her eleven grandchildren owe for what they are now to her. She taught them manners, culture, and etiquette and she took care of everyone. She laid a solid foundation for the family. She herself wished to learn English and one day in her sleep she was reciting the alphabet introduced to her by her brother-in-law and an elderly member of the family teased her about her passion for learning English; she felt so embarrassed that she gave it up from that day.
GP: With my father’s reluctant permission to study further, I applied to a few places: Patna University both for physics and for mathematics, BHU [Banaras Hindu University] and Delhi University, which was reputed to have a very good physics department, thanks to D.S. Kothari. I also applied to Birla Institute of Technology in Ranchi. Because I came first at Magadh University, I was admitted to all the places. In those days it was all about the marks.
She only had a primary education, but she championed education
So you not only got admission in all the places, you got selected for both physics and mathematics courses?
GP: I had applied to both departments only at Patna University. But in BHU and Delhi University, I applied only to physics because physics was good in those places.
Anyway, when it came to choosing a university and a subject, I chose Patna University, because Patna is so close to Arrah where my brother lived. I had studied in Arrah and Patna was hardly fifty kilometres from there. So I thought that I could easily visit my brother from there whenever I wanted.
I went to Patna with admission letters from both the physics and maths departments. It was clear to me that I was more interested in maths. But physics and biological sciences had better prospects in terms of jobs and income.
My intellectual interests won the day. I decided to pursue mathematics and got a masters from Patna University. I really enjoyed learning mathematics there, though I will not say that all the teachers were good. Some were certainly good. Among electives, I took mathematical physics, and complex function theory courses. I studied the first volume of the book on mathematical physics by Courant and Hilbert, which focused on special functions. For complex function theory I read the books by Copson and Whittaker. I learned a fair amount of applied mathematics and ordinary and partial differential equations also.
So you really enjoyed learning these topics, and also the vicinity of the place to Arrah.
GP: Yes, I enjoyed it. I stayed in a hostel called Faraday House. An interesting fact about Patna University was that we had hostels named after notable scientists, so we had a Newton House, a Cavendish House, a Ramanujan House, and so on. Most hostels at that level, masters or undergraduate, were double-seated. Faraday House alone, with forty rooms, was single-seated. Most of these rooms were given to people who had stood first in some university. So I got into Faraday House. It was a very interesting place. It was nicely built with a courtyard and big rooms. The courtyard was full of rose plants. The gardener there took good care of the plants.
I finished my masters exams, but in Patna University and also maybe in Bengal, the examination results were announced late, in the middle of August. Even if I wanted to apply, I couldn’t have applied anywhere for a PhD program. But something interesting happened.
Patna University had the tradition of offering a lecturership right away to toppers in the university masters exam. I was invited to go see the Head of the Department of Mathematics, Dr. R. Shukla, and he asked me to meet the Principal of the Science College. The Principal at that time was Dr. S. Nagendra Nath, who had earlier worked with Sir C.V. Raman. There is a short paper of Raman with Nath.4

In the meantime, I began to read on my own a book on real analysis by Simmons.
It would be Introduction to Modern Topology and Analysis by George F. Simmons, I believe.
GP: Yes, I bought that book and began reading it. I felt that Patna was not a place to pursue higher studies and that was a timely realization. Looking back, in my life, some decisions were made by instinct without real knowledge, but they turned out to be extremely lucky.
I think my decision to move from Patna saved my mathematical career. Had I continued there, I would have worked in the area of point set topology; an area that is not very active.
How exactly did the idea of studying at TIFR come about?
GP: First I went to IIT, Kanpur. It so happened that IIT had admissions also in the second semester. I was interviewed there sometime in November 1965. I was selected and I joined there in 1966 in the winter semester, January to June. There I met Ramji Lal, who came from Allahabad University and he became a close friend.
Ramji Lal and I shared several things. He was born in the same district as myself, Ghazipur. And his date of birth [31 July 1945] is the same as mine.
I heard about TIFR after joining IIT. But I didn’t know much about it, and how life-changing it would be for me to go there.
Perhaps, in 1966, Kanpur was already a place from where I guess people had gone on to study at TIFR?
GP: No. I don’t think that anyone from Kanpur had gone to TIFR until then. Ramji Lal and I applied to TIFR, and on the basis of our marks in BSc and MSc, and letters of recommendation from our teachers at IIT, we were both called for an interview. Ramji Lal’s elder brother Gopal Lal worked for the Indian Railways in Naini (near Allahabad), and he promised to get us train reservations. Because of the awful rush in trains due to the wedding season in the summer in UP and much of north India, without reservation, it was almost impossible to travel to Bombay from Allahabad. Kashi Express and Bombay Mail were the only two express trains in those days that went from Allahabad to Bombay. But it so happened that Ramji Lal’s brother forgot to make a reservation in either of them.
On the day of our journey, we learned that we didn’t have a reservation. We went anyway to Naini station. The Kashi Express usually departed in the afternoon at about 3 o’clock, and it was so full. It stopped for only three minutes. We tried various ways to enter the unreserved compartment but failed. Taking this train, we would have reached Bombay only a day before the day of our interview, so there was no question of trying to go on the next day. I was disappointed, determining that there was no way to reach Bombay in time. But Ramji Lal’s brother-in-law insisted that we take a non-express passenger train, which stopped at every station. That train was also extremely crowded, but this time we made it inside thanks to the kindness of a few people who pushed us in through the window! Packed so tightly that we couldn’t move an inch. This train went up to Itarsi. From there we caught the Punjab Mail to finally somehow reach Bombay just a day before our interview. For me, this was a life-changing event. Without going to TIFR I would have been in the mathematical backwaters, and it is impossible to imagine what would have happened to three of my brothers who later followed me. My eldest grandchild Amit, who was asked in his school (in New York) to write an anecdote about a remarkable event in a family member’s life, chose this incident for his school project. His teacher and classmates found it very amusing.
Tata Institute reimbursed the train fare but didn’t arrange for accommodation in Bombay for the interview. With our scholarship money, we could stay in a hotel on Marine Drive!
When we went to Tata Institute for the interview the next day, our turn didn’t come until late in the evening. Luckily we were both selected. In the interviewing committee, Seshadri was there. There were several others, and I remember Shrikhande who was there because it was customary for someone from Bombay University to be there, but he didn’t ask me any questions. We decided to leave IIT Kanpur and met with J.N. Kapur [Jagat Narain Kapur], who was the head of the department, to tell him that we would go to TIFR. He didn’t object or ask us to refund the scholarships we had received at IIT. We joined TIFR in August 1966.
Talking about the interview questions at TIFR, you said Seshadri and others were there. What questions did they ask you?
GP: I remember one or two questions. It was about continuous functions, uniformly continuous functions, metric spaces, and things like that. I had some understanding, and they were willing to offer me some help. To prove uniform continuity on [0,1] you had to replace a set of neighbourhoods by a finite set which is possible due to the compactness, and then you are done. There were many other questions too.
How long did your interview go?
GP: It must have been more than an hour.
And was the communication in Hindi or English, because you mentioned earlier that you learnt to speak in English only after joining TIFR?
GP: I was very insistent on learning English: At IIT Kanpur, and even at Patna University, I used to read English newspapers every day, and make a note of the words I didn’t know. I would later look them up in the dictionary and write down their meaning. That didn’t mean that my verbal English improved much, but certainly became more fluent. I could express myself better.
After I joined TIFR, it became clear to me how much better it was than any place I had seen before. In my batch, there were 18 students. In the first year, we learned the compulsory courses: algebra, measure theory, analysis and topology. These were taught by the senior members.
going to TIFR was a life-changing event
That is quite a large batch…
GP: Yes. At the end of the first academic year, we were all examined orally. After this examination, only four students were given extensions: Cowsik, Ramji Lal, Krishnaprasad and myself. Vijay Kumar Patodi also joined TIFR that year.
Ramji Lal and two others were given a one-year extension and were told that they would be examined again after a year. I was given a full extension.
When you say full extension, was this what was called a Research Assistant position then?
GP: Yes, and it was for a period of four years. I am just quoting from my memory, so roughly this is what happened. After the first year, Ramji Lal opted to leave TIFR which I thought was a big mistake, and I tried to persuade him not to leave, but to no avail. After leaving TIFR, he joined Allahabad University where he eventually became a professor and wrote some very comprehensive books on algebra.
In the first year, hostels were near the Gateway of India. Those were barracks that were used as servants’ quarters for the old Yacht club. The officers would enjoy the Yacht club and the servants lived in the quarters. That is where we lived. There were not enough rooms for everyone to be accommodated in independent rooms. So two people had to share a room, but in our batch, since it was a large batch, Ramji Lal, myself, Pathak and Krishnaprasad – four people shared a room. Two could sleep on the cot, and two others on the floor.
In those days, there was very good camaraderie. You know people like Ramanan, Raghunathan, Gowrisankaran, not Narasimhan though, all came to the hostel. These senior mathematicians lived in private apartments in Colaba. Raghunathan lived near Radio Club, near the Taj Mahal Hotel. Ramanan may have lived near the Colaba post office. They used to come and talk to people, gossip, and discuss mathematics too. And we often went together for dinner. There was one Modern Hindu Hotel, and they would serve south Indian thali with rice in limited quantities. Sometimes we would go there, but sometimes we would go to Kwality and then there was the Majestic Hotel (both in Colaba, and both now closed). It was very nice that people would come and we would talk. Even though they were already associate professors, we could meet them freely and regularly. I became somewhat close to C.P. Ramanujam. Spanier’s book on algebraic topology came out in the year I joined TIFR, and as I was interested in topology, I read this book. In case of difficulty, I would talk to C.P. Ramanujam. He was also learning topology in those days. He was pretty brilliant.
Vijay Kumar Patodi became a close friend from the first year when he was a PhD student at Bombay University. During that time he used to come regularly to attend the first-year courses in TIFR and in 1967 he joined TIFR.
What were the research options available at TIFR then, and how did you take up the study of Lie groups?

GP: TIFR was extremely good. My coming to TIFR for my research meant a lot!
Daya-Nand Verma had joined TIFR in ’67. He had a job before that, I think in New Mexico, and when he joined Tata Institute, people thought of him as someone with great potential, because N. Jacobson had written a very strong letter for him. His thesis was on the so-called Verma Modules written under the supervision of Jacobson. Verma wanted me to be his student.
I think in 1967, Raghunathan came back from Princeton, and I distinctly remember being introduced to him near the elevator on the third floor, where there is a notice board. He asked me some mathematical questions, and also what I had studied or what I was studying. In those days, I was interested in topology. Since P.J. Cohen’s book Set Theory and Continuum Hypothesis, came out in 1966, I also became interested in axiomatic set theory that year. I recall that Cohen proved that the Continuum Hypothesis is independent of the axioms of Zermelo-Frenkel set theory. This was one of Hilbert’s problems, and Cohen was awarded the Fields Medal for his proof. I read a part of Cohen’s book, but did not complete it because I got more interested in various topics in topology: fibre bundles, characteristic classes and such. When I met Raghunathan, I had somewhat of a better understanding of topology than set theory. And then Raghunathan more or less took me under his wing. He would come to my office and talk to me on a regular basis. He also gave a course on Lie algebra, a very rapid course: in about a week covering the whole structure theory.
It so happened that G.D. Mostow [George Daniel Mostow] from Yale University was going to visit TIFR in 1968 under its usual long-term visitor programme.

I studied Lie Group theory from two books, one was Chevalley’s foundational book, and then another by Hochschild, The structure of Lie groups. I followed these books very carefully, but one needs some practice to become fluent, just like in learning a new language. Nevertheless, I have been able to teach courses on Lie groups and Lie algebras just based on my knowledge of that time. Without having to carefully consult books on a day-to-day basis, I gave courses first in TIFR, and afterwards several times in the University of Michigan.
Raghunathan more or less took me under his wing
As I knew nothing of algebraic groups which comes up quite a bit in the theory of semisimple groups, (for example, it is helpful to know the work of Borel and Tits on reductive algebraic groups over non-algebraically closed fields) and had also not learned the theory of discrete subgroups of Lie groups, my writing of Mostow’s notes, I would say, was poorly done.
Raghunathan had initially suggested to me a problem in topology because he knew that I was interested in it. I had read Spanier, and I was reading Characteristic Classes from, yet unpublished, notes of Milnor; I wanted to learn some more topology.
I think you were Raghunathan’s first student, right?
GP: No, I think, technically speaking I was his second student. The first student V.J. Lal didn’t complete a PhD, but he became a very close friend of mine.
I think he went to Madurai?
GP: Yes. And after me, S.G. Dani came along. Dani is a very good mathematician. Another early student of Raghunathan was Vinay Deodhar who did some very interesting work. I have high regards for both of them.
Dani was my thesis advisor. What was the specific problem that you studied for your PhD thesis? Would it be possible to describe it, or give an idea, in simple, non-technical terms?
GP: Raghunathan initially suggested a problem on vanishing of characteristic numbers of a flat bundle which was, I would say, not very interesting since in most cases this was already proven. A flat bundle is the bundle obtained by a representation of the fundamental group. For a differentiable flat bundle, one knows that characteristic numbers, Pontrjagin and Chern numbers vanish. The reason for this vanishing is that the Chern–Weil theory tells you that these numbers can be computed using curvature form, by integrating some power of the curvature form or some polynomial that tells you right away that these numbers are zero because for flat bundles the curvature form is identically zero.
Raghunathan had wanted me to do the topological analogue of this, without the Riemannian structure. And that was also possibly being done by Illinois-based mathematicians Tondeur and Kamber—now my memory is not totally reliable on this—but there were things by them which studied flat bundles and their various topological invariants. So if you have a Riemannian manifold structure, then you immediately see the vanishing. So this was a problem which to me looked uninteresting because after all, in the good situations, one already knew the answer.
In 1969, TIFR brought out the lecture notes titled “Discrete subgroups of Lie groups” by Mostow for which you wrote notes. Did this first interaction with him trigger your later work on the Mostow–Prasad rigidity theorem?
GP: Mostow’s coming to India was a blessing for me. I developed a lifelong friendship with him and his wife Evelyn.
Mostow had written a paper which plays an important role in his work on strong rigidity. That paper, thanks to K.G. Ramanathan, was submitted to the Journal of The Indian Mathematical Society. Ramanathan gave the paper to Raghunathan to look at and Raghunathan in turn gave it to me. I spotted a small mathematical error and filled the gap for him.
Mostow’s paper studies the situation where G / \Gamma is compact, where \Gamma is a discrete subgroup of G also called a cocompact, or uniform lattice. Then it was, you know, a natural question whether this can also be done for non-cocompact lattices where G/\Gamma has finite volume, but is not compact. I mentioned this question to Raghunathan, and he said, “Yes, it is a worthwhile question to investigate.’’ And he was pretty fast and knew the subject very well. So he came up with some ideas within just a few days. He told me about his ideas, and then I made some more contributions and it finally became a long joint paper. That paper appeared in print but after removing its long fourth section, which is still unpublished. But the first three sections appeared in the Annals of Mathematics, which is the most prestigious journal of mathematics. This paper in preprint form attracted the attention of several people including Mostow. You know in those days cyclostyled copies were made, we inserted symbols by hand, and then I sent it to two or three people – Borel and Mostow, perhaps one or two others. Mostow immediately used it in his book on strong rigidity. Then he sent me a letter sometime in the summer of 1972, saying that Yale University was offering me an assistant professorship for one year. Being invited to Yale University had a big impact not only on my life, but, as I mentioned earlier, it also had a major impact on the lives of three of my younger brothers.
Curiously, I didn’t even have a PhD at the time! Raghunathan was not yet recognized by Bombay University as a thesis guide so I decided to wait. I could have formally become a student of M.S. Narasimhan for my thesis, but I felt it would not be proper. When I went to Yale, Mostow learned that I didn’t have my PhD, and he was surprised.
A paper in the Annals of Mathematics, but does not have a PhD yet…
GP: At that time, the paper was accepted but not yet published. Mostow knew that the paper had many interesting results and that Borel was also interested in it. So the paper circulated amongst some experts like Furstenberg. Furstenberg is a famous Israeli mathematician.
Mostow’s coming to India was a blessing for me
Furstenberg was awarded the Abel prize in 2020.
GP: Yes. When I went to Yale in 1972, we once crossed paths in the department and I introduced myself to him, though I had no idea that he was famous. I knew some of his papers, but didn’t know the person. He said, “I have seen your paper which is interesting’’, or something to that effect.
You must have felt extremely good! While at Yale, you proved important rigidity theorems, can you describe what these are?
GP: Yes, certainly! I was still quite young, just 27. That was my first paper, and then I wrote one more paper before going to Yale which was submitted to the Journal of the Indian Mathematical Society.
At Yale, I did two major pieces of work. The first one was on the strong rigidity of \mathbb{Q}-rank one lattices. In the cocompact case, this was already Mostow’s result. My rigidity result was proved only in the \mathbb{Q}-rank one (non-cocompact case). The reason for that was that in this case there is a nice fundamental domain constructed by Garland and Raghunathan, using some ideas of Selberg. This fundamental domain was known to me because Raghunathan had given a course on discrete subgroups before I went to Yale. In that course, he also covered the Garland–Raghunathan result. It is also fully described in his well-known book Discrete Subgroups of Lie Groups. So I knew these things very well. Sometimes knowledge is helpful and handy. My result covers all real-rank one groups. Margulis’ wonderful super-rigidity theorem doesn’t cover rank one cases; so combined with mine, we have the general rigidity theorem for all real semi-simple groups and all lattices in them.
After this, while at Yale, I proved the strong rigidity of cocompact lattices in semi-simple groups over local fields. The proof was modelled on Mostow’s proof of the strong rigidity of cocompact lattices in real Lie groups. It uses the Bruhat–Tits buildings in place of symmetric space. This was my first use of these buildings. Based on my fragmentary knowledge of the theory, I formulated certain results about them which were needed in my proof and wrote to Tits to confirm them. He replied promptly and confirmed the results. This was the beginning of my lifelong association with him.
I informed Margulis about the above result on the strong rigidity of lattices from Yale. This was the beginning of my mathematical correspondence with him, which continued until he left Moscow to join Yale. We have become good friends and, after our retirements, often talk to each other over the phone.
And that was your first trip abroad?

GP: Yes. It was in 1972, I was 27, had a toddler son and had no idea how life was going to be in the US. We had no money and in those days, one could get 8 per passenger for a trip abroad and that wasn’t enough to travel from the airport to your destination. Raghunathan gave us 100 when we were leaving and we used it to get a limo ticket to travel from JFK to New Haven. Mostow was waiting in our hotel with a few bags of groceries and a month’s salary in an envelope. What a thoughtful thing to do! He reserved a flat for us in the university housing on Prospect Street. He also bought basic furnitures for us. (Rajat Tandon, who was a PhD student there, helped us to move the furnitures to our flat.) All this made settling at a new place easy. With the first month’s advance salary, we could get the things we needed to establish a new residence with basic furniture, a crib and kitchen utensils, winter clothing etc. The Mostow’s were extremely friendly and kind to us all their lives.
Patodi and Parthasarathy visited us in New Haven. They were happy to have Indian food Indu could cook with basic groceries. Patodi invited us to visit him at the IAS. We visited him during the Christmas holidays, stayed with him for a few days, cooked Indian food together, and walked on the frozen lake at the Institute.
To talk a bit more about Patodi, at TIFR it looks like no one before him or after him worked in that field.
GP: Yes. Formally he was a student of Narasimhan or Ramanan; perhaps they were his joint advisors. But the fact is that he was no one’s student. He was self-taught. And he saw a problem about Reidemeister torsion. I think there was some conjecture known as the Ray–Singer conjecture; as these two had done some initial work on it. Patodi read somewhere what the problem was and then himself found a way to solve it. There was a book on linear differential operators by [Lars] Hörmander; Patodi mastered that book. In his student days, he used the heat equation method. He noticed some cancellation properties which then led to his work on Reiemeister torsion and later a new proof of the index theorem jointly with Micahel Atiyah and Raoul Bott.
Recently, I happened to talk to Jothilingam who mentioned that he was his officemate.
GP: Jothilingam was a great friend of mine. My economic situation was not good shortly after my marriage in 1969. So I used to borrow money from him sometimes. You know the salary was low at that time. Since I had not followed my father’s desire, I didn’t want to take any money from him. Whenever I needed money, I borrowed from Jothilingam, and I would repay him when I got my next salary. He became my permanent bank!
Taking a brief break, we would love to hear about your marriage to Indu Devi, and the ensuing family life.
GP: We got married in 1969. It was an arranged marriage. One of my younger brother Vijay Prasad’s family lives in the same town as Indu’s family. Indu was an undergraduate student at BHU.
Soon after her examination, the marriage took place and we moved to Chembur, a suburb of Bombay, where I was allotted a flat and we settled down there. We lived there for three very happy years. Indu made some good friends in the building. I regularly took a train to go from Chembur to VT station,5 and from there went to TIFR by the institute bus and came back after the rush hour, reaching home after 8 pm. Indu joined Ruia College to continue her study.
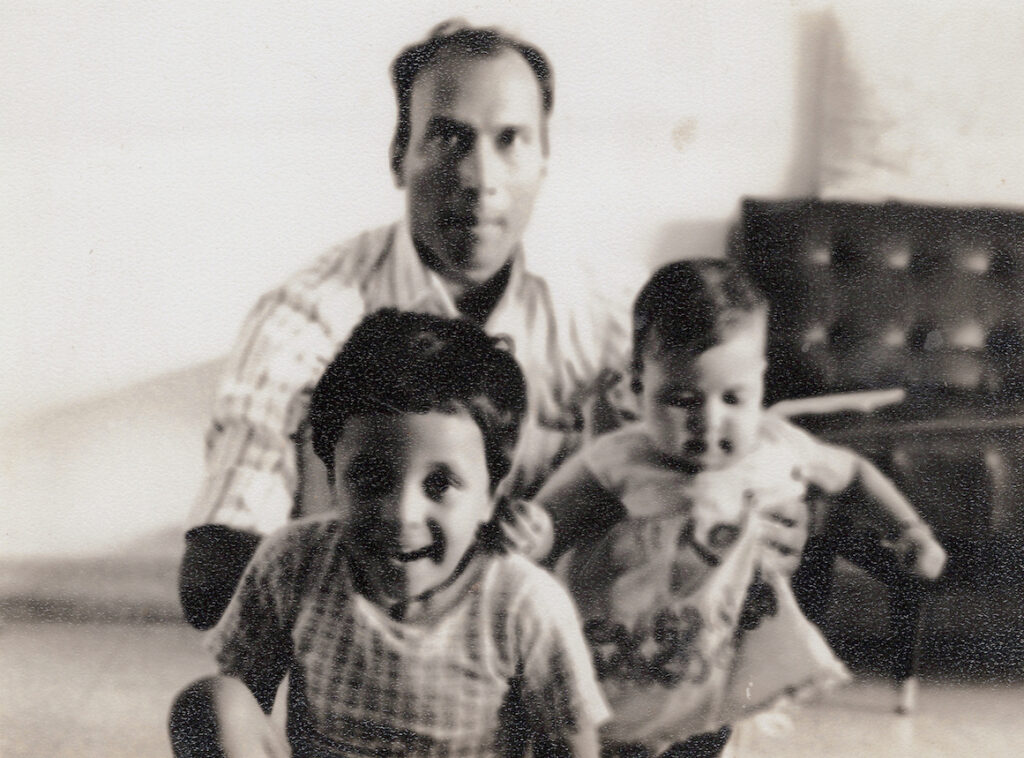
At the time of our visit to Yale in 1972, we had been married for three years and our son Anoop was a toddler. Here, I would like to mention Indu’s contributions to our family. Everyone raises one’s own children, but she simultaneously took care of two of my younger brothers too; she has been a very positive influence on all of us. And in my opinion, raising one’s own children is easier than raising a mathematician—I realized early on that I could not manage to live by myself, therefore I almost always travelled with my family. In one’s life, there are many ups and downs and Indu has been my total support in every possible way. We were the first one in the family to settle in Bombay, therefore we often had family members, as well as others, come for sightseeing and also for work related to their business, and stay with us.
Yes, it must definitely be a tremendous support, I reckon…

GP: Returning to mathematics, I spent the year 1972–73 at Yale where I proved strong rigidity for \mathbb{Q}-rank one lattices, and it appeared in Inventiones Mathematicae. I also proved it in the p-adic case, the same result which, of course, is contained in the later work of Margulis and also perhaps Gromov. You know they did that by different methods. I used Mostow’s method and used Bruhat–Tits buildings rather than symmetric spaces. So there are certain simplifications and certain difficulties which one has to face. This paper was written at the IAS in 1973 and published in Studies in algebra and number theory.
In the first semester, I had to teach one undergraduate course at Yale. Then IBM gave me a fellowship, which I had not applied for, perhaps through a recommendation by the department. I did not know about it. But in any case, in the second semester, I had no teaching responsibilities and I made good use of that. In April and May of that year, Grothendieck was coming to the State University of New York at Buffalo and I asked Mostow about attending his month long course on algebraic geometry and algebraic groups. He said it was a good idea. To attend the course, Indu, Anoop and I went to Buffalo for a month.
raising one’s own children is easier than raising a mathematician
It would surprise many who read this that before going to Buffalo, I already had several conversations with Grothendieck when he came to TIFR to participate in a very famous International Colloquium on Algebraic Geometry in 1968, which was attended by many luminaries. Grothendick had come there after visiting war-torn Vietnam, and by that time he was disillusioned with mathematics. In his conversations with me, he tried to convince me, a second-year student, that science and technology are useless, and even harmful, and India should not be spending any money on research in these fields. He also said that India should follow Mahatma Gandhi and focus on developing cottage industries in villages.
After he went back to the IHES [The Institut des hautes études scientifiques (in English: Institute of Advanced Scientific Studies)], I received a large parcel from him. It contained all the SGA [Séminaire de géométrie algébrique] volumes, and also his writing on Vietnam. I left these volumes at TIFR, since I did not think at that time that I would ever use SGA. I was proved wrong as I have been using SGA3 for 25 years now.
We note that Armand Borel and you shared many decades of friendship and professional interests. What common mathematical interests brought the two of you together professionally, after you first met him in 1972 while visiting Yale?
GP: Both of us were interested in rigidity questions, arithmetic groups, representation theory of reductive p-adic groups and geometry.
The way the first meeting with Borel happened is quite amusing, so I will narrate it. During my visit to Patodi during the Christmas holiday in 1972, he asked me if I would like to see Armand Borel. I told Patodi that it would be wonderful to meet Borel. He is an expert in my area and is a very famous mathematician. I went with Patodi to see Borel in his office. The day was Saturday. (Borel used to type his manuscripts in his office at the IAS on Saturdays.) As expected, he was typing. After introducing me to Borel, Patodi left. My meeting with Borel lasted for over an hour discussing rigidity and arithmeticity. He asked me a few mathematical questions, about arithmeticity and so on. He did it to learn, not to examine me. At the end of the meeting, Borel asked me if I would like to come to the IAS for a year. I readily accepted the offer. He wrote a letter of recommendation for me, and I got an invitation to visit the IAS during 1973–74.
Borel and his wife Gaby were always very kind to me and Indu. We visited each other in Princeton, and before he retired from IAS, he invited me there again in 1981–82, and 1987–88. He also visited me in Ann Arbor. Borel had a reputation for being a very tough person. In mathematical conversations with him, he certainly did not like imprecise statements.
He once told me that he usually answered all letters with mathematical results or questions, since, he said, some Cambridge mathematicians to whom Ramanujan had sent his results before he sent them to G.H. Hardy, did not respond. If Hardy also had not responded, Ramanujan would have probably died in obscurity.
Indu and I had a very happy year at IAS. I learnt some mathematics from visitors who came, and at the institute tea time, I would sit, for example, with Gersten, a K-theorist who was an expert on Quillen’s K-theory, to learn the basics of that theory. Bill Casselman was also there. He gave me a preprint of the Casselman–Wigner paper which became very useful in my later work on central extensions. So that was a fruitful year. In 1987–88, I even collaborated with Borel.
By the way, when Borel fell terminally ill, I went to see him in his house. We talked for quite some time. It so happened that he passed away that night. Thus, unfortunately, I became the last person, outside his family, to see him last.
Did that year 1973-74 at IAS coincide with Patodi’s stay there too?
GP: No, Patodi was there in the previous two academic years.
And was it during this time that you also first met Harish-Chandra? You have had close interactions with him, quite literally a tall figure in the theory of Lie groups and their representations. At this significant moment just past his hundredth birthday, we would like to hear reminiscences of your interactions with him.
GP: Yes, he invited us to dinner at his house. (Invariably, we would be invited to his house on the Thanksgiving holiday, even later after his passing away in 1983, by his wife Lily.) And he too came to our house in Princeton for dinner. Though he was very formal and kept aloof from most people, in his own way, he was quite nice to me.

But on the other hand, I can’t tell a student not to carry excess baggage: A student has to have a good understanding of some parts of mathematics at least. Harish-Chandra was extraordinarily gifted and not everyone can be as creative and “travel’’ as light as him, so I take his words, but not too seriously, because sometimes extra baggage can be useful. In fact, his remark would not apply to some of his own colleagues. Take the case of Borel who knew a lot of mathematics. He created a lot of mathematics to be sure, but he also knew a lot of mathematics.
We returned to India from IAS in the summer of 1974. My proof of strong rigidity of lattices in groups over non-archimedean local fields, when this local field is of positive characteristic, I needed a proposition which I tried to prove while in Princeton. After returning to Bombay, I could prove it. I realised suddenly one day that that proposition proves, or it can be used to prove, the so-called strong approximation property. This is an important result. It was proved in 1975.
By then you had submitted your thesis as well? I mean when you came back, Raghunathan was already an officially recognized guide?
GP: Yes. I submitted the paper on strong rigidity for p-adic groups as my thesis after returning to TIFR. The reason is that it was already typed at the IAS, and it was of reasonable size, something like 80 pages. T.S. Bhanumurthy was the external examiner. He conducted my oral examination in Raghunathan’s office.
I slowly started to move towards the arithmetic side, after proving the strong approximation property, which is in some ways very useful in the arithmetic theory of semi-simple groups, though it is proved using ergodic theory and so on. (That paper was also published in the Annals of Mathematics.)
After I returned to TIFR in 1974, I began reading an important preprint of Raghunathan’s on the congruence subgroup problem for isotropic groups. It kindled my interest in the problem. The congruence subgroup problem has two components. There is an extension constructed by Jean-Pierre Serre. The first, purely group theoretic component is to show that this extension is a central extension, namely the kernel of the map, which is called the congruence kernel, is a central subgroup. The second component is to determine this kernel. For this, one needs to determine the central extensions of the group of rational points of semi-simple simply connected groups, and also of the adele group of groups over global fields. One needs some cohomology computations. I had read the paper of Casselman and Wigner, in 1973, without realising that it would ever be of use to me. But it later became useful to know, from that paper, cohomology computations using Bruhat–Tits theory. Now, since I knew these things, I mentioned to Raghunathan that one can try one’s hands on computing precisely the central extensions. And that became our project for almost ten years.

In 1980–81, I went to IAS for the second time. At that time, together with Raghunathan, I was primarily focused on determining the topological central extensions of the group of rational points of semi-simple simply connected groups over non-archimedean fields. As there was considerable progress on this problem while I was at IAS, I began writing up the first (but still incomplete) draft there. During that time, I learnt the finer details of the Bruhat–Tits theory just by experimenting with it. Because the famous second volume of Bruhat–Tits IHES paper had not yet been written, I had to work out many details by myself. The paper was completed, after I went back to Mumbai, and published in the Annals. It is quite long (125 pages!), and it uses quite a bit of Bruhat–Tits theory. We were lucky that things worked out.
In 1981 while I was in Princeton, the University of Notre Dame invited me for a month or so. Timothy O’Meara, who wrote a famous book on quadratic forms, was the provost. He must have known my work on strong rigidity somehow, or at least heard of my name. While there, I was asked to give two or three seminar talks. I decided to speak on the arithmetic of semi-simple groups and wanted to work out something new for my lectures. There was the Kneser–Tits problem. I found a solution to this problem over local fields there. When I came back in 1981 to Bombay I showed this proof to Raghunathan. Raghunathan said, “Yes, it is very nice. Maybe you can do it over general fields.” Kneser–Tits problem is quite interesting for local fields. I found a proof that reduces the solution to groups of rank one. From classification over local fields, we know that there are five families of groups that have rank one; each one of them is a classical group for which you already know Kneser–Tits. So the technique I developed was a technique of reduction to rank one. Raghunathan suggested that I find the same reduction over general fields.
Was the rank one case known?
GP: No. Over general fields, there are many more groups of rank one. For number fields, there are already many more. I started to work on reduction to rank one and finally found a proof with some help from him. Suslin came to TIFR and I had some useful conversations about quadratic forms with him – mathematics is not developed in a vacuum. I completed the paper on rank reduction for the Kneser–Tits problem in 1983. It is a short paper. Raghunathan was going to the IHES, and he wanted to read the paper before it was submitted for publication. When it was submitted to Commentarii Mathematici Helvetici, the Swiss journal, it was accepted and published in 1985.
I think you wrote a series of some six or seven papers with Raghunathan.
GP: Yes, six papers. Two of them are in Annals of Mathematics. There are two in the Inventiones, one of which is almost 50 pages long devoted to the central extensions of SL_1(D), and the other paper is on the finiteness of the metaplectic kernel.
In 1986, I visited MSRI [Mathematical Sciences Research Institute], now known as The Simons Laufer Mathematical Sciences Institute (SLMath) at UC Berkeley for one year. Before that Borel had invited me to ETH, Z”{u}rich for six weeks. There, Borel told me about a problem that Tits had suggested to him. It is somewhat technical to explain: Given a semi-simple group over a non-archimedean local field, there is an associated Bruhat–Tits building, and you have chambers in the building. The question is, what are the discrete subgroups of the given semi-simple group which act transitively on chambers of the corresponding building? W. Kantor and Tits had completely classified such groups. But Tits’ hunch was that it might be possible to prove more general results. Not just chamber transitive but something more. I had some ideas, and those ideas ended up working in most cases. We made an announcement in Compte Rendus Acad of Sciences of France. That announcement was written from Berkeley, MSRI.
While trying to improve the results, I thought that it would be nice to prove a volume formula. If you can get the formula for the volume of G/ \Gamma, that would be nice. The wide use of such a formula was not so clear to me then, but I thought that it would be very attractive and then I found the formula. This formula is quite well-known and turned out to be quite useful. This volume formula was proven in 1986–87. And then Borel invited me to IAS again, the third time. So 1987–88 was spent at Princeton, and there I collaborated with Borel on two projects. Using the volume formula we proved several deep finiteness theorems. These say, in particular, that if you bound volume, then you have only finitely many possibilities. And then there was a preprint of Margulis on the Oppenheim conjecture. Borel and I ran a seminar at the IAS, and while learning Margulis’ wonderful proof we found some simplifications in the proof and generalisation of his result. So altogether 1986–88 were quite fruitful years.
It makes me very happy to see my volume formula being used by many mathematicians in many different contexts.
Was that your first collaboration with Borel?
GP: With Borel, yes this was my first collaboration. There were two announcements, one on Tits’ question and another on the Oppenheim conjecture. And we wrote two long papers.

In a rather surprising move perhaps, you left TIFR in 1992 to join the mathematics department of the University of Michigan at Ann Arbor, where you have had a long stint and are now the Raoul Bott professor emeritus of mathematics. How did this shift come about?
GP: As I have already mentioned earlier, I made a third extended visit, with my family, to the USA, first to the MSRI at UC Berkeley in 1986–87, and then to the IAS in Princeton in 1987–88. In 1989, I received an invitation from the University of Michigan out of the blue, asking if I would consider relocating there. They asked me to come for a year to see what I thought. Having returned only the previous year from Berkeley and Princeton, and with the children in schools in Bombay, another year of leave was impractical, so I took one semester of leave, and Indu and I went together to Ann Arbor, leaving our children in the care of my younger brother Dipendra. We liked the visit and found that the mathematicians there really cared for us.

Indu Prasad He went to Chicago to give a lecture, where Raghavan Narasimhan talked to him. He told me, “What is stopping Gopal from accepting the offer of the University of Michigan? I see a hesitation in him’’. He said, “It is a big decision yes, but he has proved himself, he doesn’t have to prove again, if that is what he is worried about…”
GP: Yes, Raghavan Narasimhan encouraged me to accept the offer from the University of Michigan.
TIFR had been a boon in my early work. Over time, as I became more senior and took on the role of the Dean, I was faced with a difficult administrative situation. I noticed frustration among some older, and not-so-active, members. Some people had reached the top of their pay scales and were frustrated at not being promoted to the next level because they weren’t active in research.
My philosophy at that time, as also now, is that if you employ a person in an institution then you should keep him/her happy. One frustrated person will make three others frustrated. I tried to correct the situation by offering pay grades similar to the ones in the Department of Atomic Energy (DAE), and I did this with the help of DAE. Most people were willing to accept this solution, but some others were not. Some professors thought that promoting people to the rank of professor would amount to diluting the prestige of TIFR. So, this was an argument put forward by some. I said to them, “Do you think that anyone ever asks you what your position is at TIFR? People never ask when they invite you. I mean I went to various places without even a PhD; I was never asked what my post was’’. But the tensions remained and I was not happy to spend so much time on administration and still ending up with dissatisfied colleagues.
How has it been since you moved to the US?
GP: My going to the US has been very good for me mathematically. This includes the six visits to Yale, IAS and Berkeley at various times, but also going to Ann Arbor permanently was very useful because soon after I went there, I invited Andrei Rapinchuk from Minsk. I have a long and very fruitful collaboration with him. We have written over a dozen papers, several of which have turned out to be quite influential. Among the things we did together were computation of the metaplectic kernel, Galois cohomology, existence of generic elements and their various applications including to the study of weakly-commensurable arithmetic subgroups and the question of whether isospectrality implies commensurability for compact locally symmetric spaces.
So your time at Michigan has been very productive…

GP: When I went to Michigan, an early collaborator there was Allen Moy. He worked in the representation theory of reductive p-adic groups. I hadn’t worked in this field until then. He had asked me some questions back in 1986, but then I got busy with other work and so did not think about his questions. When I joined the University of Michigan in 1992, he asked me those questions again. We collaborated on three papers, two were published and have become very basic in the representation theory of reductive p-adic groups. Our theory is now widely known as the Moy–Prasad theory.
I wrote two papers with Jiu-Kang Yu, the first one, published in Inventiones, completely answers the following question: Given an action of a finite group F on a reductive group G over a discretely valued Henselian field k, when is the fixed point set under F, in the Bruhat–Tits building of G, the building of the identity component of G^F? The second paper with Jiu-Kang Yu was published in the Journal of Algebraic Geometry, and was written to answer a question of Kari Vilonen. The main result of this paper is crucial for his joint work with I. Mircovic on Tannakian description of the Langlands dual.
Around 2008, I began my collaboration with Ofer Gabber and Brian Conrad on the structure and classification of pseudo-reductive groups. This was a problem which Tits wanted to settle and he ran a two-year-long course at Collège de France. He was a great mathematician, but this work couldn’t be completed. He did construct several very interesting examples though.

As I said earlier, Brian had been corresponding with Ofer Gabber, but there was little progress. I was away in Princeton, and when I came back to Ann Arbor, Brian invited me to join in the project. After I joined, luckily things started to move very fast, and then we published our first book on the topic in 2010 on Tits’ 80th birthday, to whom the book was dedicated. After that, I realised how to complete the characteristic 2 cases mostly left open in the book, and that resulted in the second, much expanded, edition of the same book.
The point is, in mathematics sometimes very heavy machinery may not work. You sometimes need to know things about, maybe, the internal structure of the thing, or a different angle, not the machinery. And my joining the project probably brought in this kind of expertise in algebraic group theory. Later, Brian and I were able to obtain a complete classification of pseudo-reductive groups. This classification was published as a Annals of Mathematics Studies book in 2016. Brian is a very good writer. And he is willing to write as many times as is required to give a proper exposition.
Seated here in the ICTS-TIFR campus in Bengaluru, we note that you are here for a seminar on Zariski-dense subgroups, of which you are one of the organisers. Some of your work in this area has been done
in mathematics sometimes very heavy machinery may not work
while working in close collaboration with Andrei Rapinchuk. What are some noteworthy mathematical takeaways from your joint work with Rapinchuk?
GP: As I mentioned earlier, I have had an extremely fruitful collaboration with Andrei Rapinchuk. I have already listed some of the results we obtained together. Andrei is a very original mathematician. He has made important contributions both independently and jointly. You may know that our work on the existence of generic elements in Zariski-dense subgroups (of semi-simple groups) has turned out to be quite useful. It has led to many interesting developments in the field.

Very recently, Andrei, with two other mathematicians, used generic elements and some number theory to prove that a Zariski-dense subgroup cannot be boundedly generated just using semi-simple elements. This is a very surprising result with a beautiful proof.
You have had a prolonged interest in Bruhat–Tits theory starting from the ‘70s. In late 2022, you have even authored, with Tasho Kaletha, a massive 750-page book on this topic, suggesting a new approach. In a nutshell, what is “Bruhat–Tits theory”?
GP: Bruhat–Tits theory has been used in several of my papers. I was a user of algebraic group theory, and then I became a contributor by working on the structure and classification of pseudo-reductive groups. That is hardcore algebraic group theory. And then I was a user of Bruhat–Tits theory for a very long time. In fact, I had been a user even before the Bruhat–Tits volumes were published. I think due to this, Tits was always very nice to me. Some of the results in Bruhat–Tits theory, for example the boundedness criteria, are obtained after a considerable amount of work, I could prove them simply and directly. More recently, I developed a totally new, and more geometric, way to do certain things in Bruhat–Tits theory itself (including the unramified descent), and so our new book is devoted to developing Bruhat–Tits theory, in my way. And that is really useful because first of all there was really no book giving the complete theory in a comprehensible form. Even French mathematicians complained that they didn’t understand the theory even though the Bruhat–Tits papers are all written in French. So I think this new book fills a gap in the field…. And it is a very useful theory. For example, the proof of strong rigidity, determination of central extensions, and volume computation, all require quite a bit of Bruhat–Tits theory.

There are infinitely many possibilities for numbers fields underlying the arithmetic structures, and for each possibility, there are countably many possibilities for the forms of PU(2,1), and so altogether there are infinitely many possible cases. So in our work to determine all fpp [fake projective planes], Sai-Kee Yeung and I needed to cut it down to a reasonable finite list using my volume formula and several number-theoretic estimates. At the end, we proved that there are 28 nonempty classes of fpp. But then with extensive computer-assisted computations, suggested in our Inventiones paper on fpp, Donald Cartwright and Tim Steger finally determined a complete list of 50 (up to real diffeomorphisms) fpp. As each of them carries two distinct complex structures, up to holomorphic isomorphisms there are exactly 100= 10^2 fpp. When I sent Mumford the preprint of our fpp paper, he congratulated us and said, “Marvelous results! I am amazed that you can get such explicit results”. Our work led to the discovery of an exotic smooth complex projective surface whose Euler–Poincaré characteristic is 3, but which is neither an fpp nor is it the complex projective plane. We named this surface “Cartwright–Steger’’ surface to acknowledge the computations by Cartwright and Steger.
We then also looked at a natural higher dimensional generalisation of fake projective planes. These are locally symmetric spaces with the same Betti numbers as their compact dual. We showed that there are just a few of them, and found 4 explicit examples.
Can you reflect a bit on your general discussion with Harish-Chandra?

GP: For arithmetic subgroups of classical groups, André Weil had some lecture notes from Chicago. He gave a few lectures in Paris on these groups which Harish-Chandra attended. Weil described some partial results on arithmetic subgroups of classical groups, mostly due to Minkowski, Siegel and others. From Weil’s lectures, Harish-Chandra realized that the results are not only partial, but the proofs are ad-hoc. He could solve the problem right away for the adjoint group (that is, a semi-simple group whose centre is trivial) by a uniform and very beautiful method. He communicated his result to Weil by mail. Weil then wrote to Borel, who was on a holiday on some island, about Harish-Chandra’s result by postcard. On his return, Borel stopped in New York to see Harish-Chandra (who was a professor at Columbia University at that time). By that time Harish-Chandra had a mental breakdown so he gave Borel the handwritten manuscript containing his results and proofs and told him that he could do with the manuscript whatever he liked. Borel generalized Harish’s result for arbitrary reductive groups and published the famous Borel–Harish-Chandra paper on Arithmetic Groups in the Annals of Mathematics.
Unlike most mathematicians, Harish-Chandra could deal with general semi-simple groups without working-out particular examples.
This must be 1959–60, I think…
GP: Yes. Harish-Chandra was feeling very low. He told me that he couldn’t even feel the strength to get up from the bed. Harish-Chandra had very good handwriting and he would write down each step of a proof. So he gave the manuscript to Borel and told him to do whatever he liked with it.
Thanks to a good physician who treated him in New York, Harish-Chandra recovered rather quickly.
The paper with Borel on arithmetic groups is the only joint paper of Harish-Chandra in mathematics. I would say that most of its principal results are due to Harish-Chandra.
Harish-Chandra wanted Indian mathematics to develop, and he felt that one institute of the TIFR kind was not enough for such a large population. So he thought that some good mathematicians should be going to other universities to help improve the quality of those universities. He suggested to me that I go somewhere else. Then I told him the story of Patodi. The physician treating him felt that he might benefit from a drier climate with his kidney problem. So he applied for a position at BITS Pilani. The letters of recommendation were written by Atiyah and Bott, and probably Singer as well. Sadly, his application was not even acknowledged properly. But the most unfortunate thing is that in December of 1976, after Patodi passed away that year, there was an Indian Mathematical Society meeting in Kerala, and the Head of the Department of Mathematics at BITS Pilani lamented that it was a pity that Patodi could not come to BITS Pilani despite their best efforts!
That is completely misrepresenting the fact [by BITS].

GP: Indeed. The fact is that it was not even acknowledged that he had applied. Patodi had told me this himself once, that when this head of the department met him in some place and Patodi enquired about his application, he said maybe my clerk has misplaced it. That feels like a lame excuse. André Weil has said that first-rate mathematicians choose first-rate mathematicians, but second-rate mathematicians choose third-rate mathematicians.
Another high point in your career has been this invitation to speak at the prestigious International Congress of Mathematicians (ICM). You spoke on “Semi-simple groups and arithmetic subgroups’’, in the ICM of 1990 held in Kyoto, Japan. How do you reflect on your experience participating as an invited speaker at a big event like the ICM?
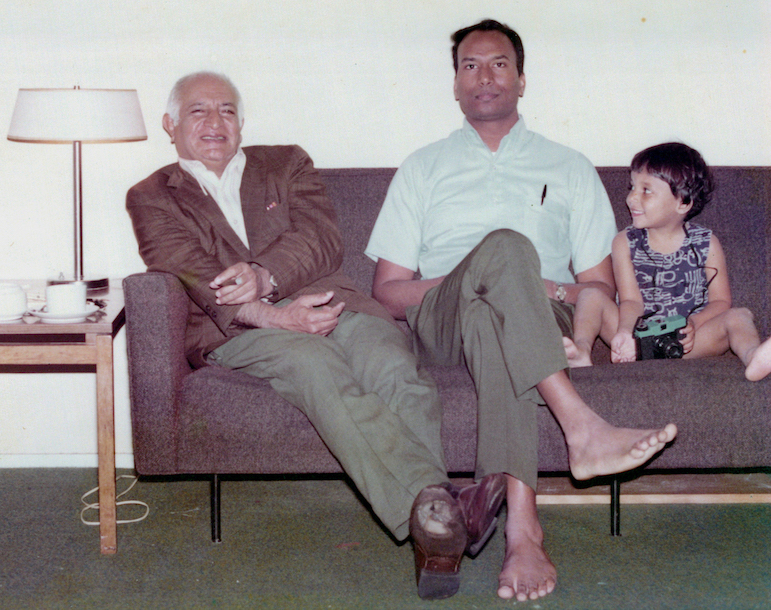
GP: Yes I gave a talk in Kyoto in 1990 and, as is to be expected, I was very happy to have been invited to address the ICM. It is considered an honour to be invited to speak at the ICM.
Let us now talk about the professorship instituted at the IAS in your name. Was it a surprise to you that the children endowed it? How do you feel about it?
GP: I was informed only after all the formalities were completed. It came as a very pleasant surprise to be honoured this way. Anoop got the idea of instituting a professorship in my name at the IAS. He also has the financial resources for that. He discussed the idea with his sister Ila, who was thrilled with the idea. They approached the IAS, which was very happy with the proposal to name the professorship after a frequent visitor to the Institute.

The connection of the Prasad family with the IAS is pretty strong. I have spent six years there as a member at various times. Pawan spent six years there as a professor, and both Shrawan and Dipendra spent more than a year each. Anoop and Ila have fond memories of their stay in Princeton, and Ila was offered a professorship at the university there.
But your coming to mathematics seems to have a big contribution to academics from a business family. Two of your brothers are mathematicians themselves.
GP: Yes, I am very happy that in my family now there are 10 PhDs and even happier that the daughters and daughters-in-law of the family went for higher education, and some of them now are professionals.

Indu Prasad: It has altered the course of family life. There has been a shift from business to academic and professional pursuits. Only two of his brothers remain in business now. Most of his nieces and nephews have gotten higher education in India and US earning PhD are other professional degrees, and most are in north America. We have a family reunion in the US every two years or so. We are happy that every time about fifty members are able to participate in it.
One can clearly discern that Indu ji’s role in the academic accomplishments of the family has been very crucial.

GP: All my books acknowledge her role. When she needs to be tough, she is tough. She is an equal partner. In India, you know one talks of luck or fate. But I believe that fate is shared by the two of us. That is, what I have achieved, I could not have achieved without her. From the day she came into my life, she has been a pillar of support.
In 1969, my parents came to visit us in Chembur, soon after we moved there, on their way back from Chennai, where they had gone for a business meeting. My father was upset with our very basic living conditions, and told Indu in my absence, “Bahurani [daughter-in-law], what is Gopal doing here, hardly earning enough, living a hand-to-mouth existence? Why don’t you persuade him to join me in the family business and have a comfortable life?’’
Indu Prasad: But I never mentioned this to Gopal…
GP: She never told me because she thought I would be upset.
That calls for a lot of inner strength.
GP: I agree. Though the life of an academic was not financially easy, it has been very rewarding for me in many ways. I hope the journey has been worth it for her and the rest of my family.
I take this opportunity to express my appreciation to everyone in Anoop and Ila’s family for their love and support in every way. After I retired from the University of Michigan in 2017, Indu and I have been enjoying extended periods of time with them.
I thank Professor R. Sridharan for his wise counsel whenever I needed it.
I thank C.S. Aravinda and his colleagues Rajesh Akkihal and Sumitra Satyavolu in the Bhāvanā team for their very pertinent questions and for their editorial work.
Thank you very much both of you for giving your precious time to talk to us, and for insights into the remarkable success story of your life. Our aspiring readers are sure to draw inspiration.\blacksquare
Footnotes
- In 2018, Allahabad was renamed Prayagraj. ↩
- Founded in 1923, Gita Press is an Indian book publishing company. Headquartered in Gorakhpur in Uttar Pradesh, it is one of the largest publishers of Hindu religious texts. ↩
- This is an arrangement where the buyer makes an initial down payment and pays the balance plus interest in instalments. ↩
- Raman–Nath theory: With his student, S. Nagendra Nath, Sir C.V. Raman provided the theoretical description of the acousto-optic effect (light scattering by sound waves) in a number of articles which resulted in the Raman–Nath theory. This effect has enabled optical communication components based on laser systems through the use of modulators and switching systems. ↩
- Victoria Terminus then, is now called Chhatrapati Shivaji Terminus. ↩
