Computing Processes and Pāṇini’s Aṣṭādhyāyı̄

It is hard to imagine that concepts that originated some 2500 years ago, find a semblance with modern concepts whose environment is drastically different from that which existed so far back in time.

Introduction

Language is a vehicle used by mankind to express emotions, experiences of the world, and thoughts. It provides humans with an ability to exchange verbal utterances (as in a spoken language) or symbolic visuals (as in a signed language). A language can be encoded into secondary media using auditory, visual, or tactile stimuli-like structured sounds, whistling, signing, or braille. In other words, human language is modality-independent, and written or signed language is the way to inscribe or encode natural human speech or gestures. Depending on the philosophical perspectives regarding the definition of language and its meaning, when used as a general concept, a “language” may refer to the cognitive ability to learn and to use systems of complex communication, or to describe a set of rules that makes up these systems, or the set of utterances that can be produced from the set rules. All languages rely on the process of semiosis to relate signs to particular meanings. Oral, manual and tactile languages contain a phonological system that governs how symbols are used to form sequences known as words or morphemes, and a syntactic system that governs how words and morphemes are combined to form phrases and utterances.

India’s rich linguistic heritage can be seen in its, possibly the longest surviving, oral tradition¹ of several Sanskrit texts. The Ṛgveda and certain later compositions of remote antiquity, together called the Vedas—believed to have been classified into four branches by Sage Vyāsa, thus earning him the epithet Veda Vyāsa—have come down to our times as very precisely intonated, blemish-free chants.

The two celebrated epic poems—the mahākāvyas, Rāmāyaṇa of Sage Vālmı̄ki and Mahābhārata of Sage Vyāsa—each running to several thousand verses or ślokas are also believed to have come down through generations via the oral tradition. In the typical traditional storytelling form associated with much of ancient Indian literature, the story surrounding the composition of the Mahābhārata is that Vyāsa wanted someone competent to scribe while he composed down. That’s when Lord Gaṇeśa is supposed to have offered his services with the condition that once he begins his taking down, he will not stop until the end, to which Vyāsa was acceptable with his own cleverly posed condition that from time to time he will recite his verses in coded or cryptic form that should be deciphered by Gaṇeśa himself as he took them down, perhaps buying his own time to compose his verses!

The technique used to ensure a high level of fidelity while transmitting the Vedas, orally from generation to generation across centuries, is to devise many combinatorial methods of rendering each line and verse of the text. In addition to the normal, continuous recitation of the Vedas, called the saṁhitāpāṭha, there are multiple techniques, where the words are combined in phonetic and euphonic ways, such as the padapāṭha, in which a pause is applied after each word during recitation. There are other traditions where the words are permuted and combined in definite patterns, called the kramapāṭha, the jaṭāpāṭha and the ghanapāṭha² and so on. Indeed, there are ten such ways of rendering the verses, and Vedic scholars who have memorised the saṁhitā and the padapāṭhas, and know the definite patterns of each of these variations,³ can recite them in one continuous flow. This ensures that any error that creeps into a recitation is automatically corrected with reference to other types of recitations.

In short, some of this ancient literature has propagated over a long period of time in the oral tradition with very few aberrations. Since the language of narration alluded to above is essentially in Sanskrit,⁴ one natural instinct would be to explore, in certain detail, the kind of techniques developed, evolved and documented in Sanskrit. The linguistic traditions of Sanskrit and other Indo-European languages were famously referenced by the English philologist and Judge Sir William Jones in a lecture to the Asiatic Society in Calcutta on February 2, 1786:

Similar explorations across the world have led to the study of language as an important branch of philosophy. Such a linguistic turn was a major development in Western philosophy during the early 20th century, the most important characteristic of which was the focusing of philosophy and the other humanities primarily onto the relationship between language, language users, and the world.

India’s rich linguistic heritage can be seen in its possibly the longest surviving oral tradition

The great scholar named Pāṇini, who lived around 500 BCE, in the Gāndhāra region, formalised the grammar of the entire Sanskrit language in his celebrated work, the Aṣṭādhyāyı̄. It is remarkable that the text, except for a few variant readings and interpolations, has remained intact, at least regarding its functionality. We shall not discuss reasons for variations of sūtras in the Aṣṭādhyāyı̄ that have again been largely handed down (see [30]) through generations by oral tradition. The seminal treatise consists of 3,959 rules organised into eight chapters.

Computing has also been an ancient activity. Several pieces of evidence of computing can be found from counting, notions of time and calendars, calculations of astronomical, astrological, navigational or urban or temple infrastructural planning requirements and such. Even various mechanical devices existed to support calculations.

However, the modern formalisation of the notion of computing can perhaps be traced to the attempts to solve David Hilbert’s “Entscheidungsproblem” or the decision problem for first-order logic. Kurt Gödel’s famous paper On Formally Undecidable Propositions of Principia Mathematica and Related Systems sealed the fate of Hilbert’s programme, as well as the grand aim of Bertrand Russell and Alfred North Whitehead, that there is no complete and consistent set of axioms for all of mathematics. There were several notions of “effectively calculable” during the 1930s. In the 1930s, Alan M. Turing came up with a mechanistic model of computing that was rooted in how humans carried out calculations while leaving out everything irrelevant to the task; for example, children learn how to follow procedures of arithmetic operations, geometrical calculations, solving equations etc.

Turing’s proposal was a minimal set of five actions that a person needs for carrying out a computation. He established that those actions and deciding between them could be done in a way that required no human intervention—i.e., they could be done in principle by a machine.

What does computing have to do in the discussion of a topic like language analysis? In keeping with the rationale of the quote of Edsger Dijkstra, “Computer Science is no more about computers than astronomy about telescopes”, this is an expository article to reflect on the ideas underlying the Aṣṭādhyāyı̄ in building a grammar for Sanskrit by Pāṇini for both Vedic (oral tradition) and written forms. An important point to note is that for Sanskrit, “words” play a vital role,⁵ as emphasised by Sage Patañjali. Such an exploration would lead to an understanding of the cognitive computing processes a person would normally do for a good speech act. It is not unlikely that such an understanding could also lead to a discernment of how children learn a language and refine their knowledge continuously, using the underlying ubiquitous computations (which could be like “bootstrapping” compilers).

Pāṇini captured the underlying abstract computations that needed to be done (mentally) for either spoken or written sentences. Further, he captured these abstractions and generalisations through succinct notations. This appears to conform with the way “effective computing” was abstracted by Turing. Looking back after several discoveries in computer science, linguistics, mathematics and information theory, one can see how several abstractions found in the modern formalisation of the notion of computing can be related to the expounding through the sūtras posited in the Aṣṭādhyāyı̄, as explored in [27], [17] and [21]. Further, a succinct notation plays a vital role in computer science (particularly in the logical aspects of computer science) and in mathematics. Some of the illuminating examples found in the Aṣṭādhyāyı̄ are: striking resemblance to the Backus-Naur Form (BNF) notation [16], which is an illustration of the syntactic description using metarules, optimality of Pāṇini in his ordering of the phonological segments to represent natural classes of intervals [29] and the richness in knowledge representation [4].

There is a vast amount of literature that relates to the linguistic aspects of Sanskrit, adaptation of the grammar to other natural languages, both Indian and European, and relationship to modern computer-based sentence generations (see [12],[15] and [14]). However, there has not been much literature about the intrinsic “formal methods” used by Pāṇini to accomplish his goals. Understanding these will bring out the significance of Pāṇini’s approach that may aid in understanding, processing or learning natural languages. The work of Kadvany [17], whose goal is to relate the Pāṇinian grammar to modern computation is an exception. One may also recall here the correct forecasts, to an extent, of the possible stumbling blocks of machine translation by the philosopher Yehoshua Bar-Hillel [26]. In the context of Fully Automatic High Quality Machine Translation (FAHQMT), he highlighted issues like “the need of semantics, limitations of logic as well as un-attainability of a database of knowledge”. Some of these aspects should be kept in mind while looking at the knowledge representation feature in the Aṣṭādhyāyı̄, and also the databases used in Pāṇini for the formation of preferred sentences.

A Brief Summary of Grammatical Concepts prior to Pāṇini

Pāṇini’s grammar [19] seeks to provide⁶ a consistent, exhaustive, and maximally concise formal analysis of Sanskrit. It is arguably the most complete generative grammar of any language yet written. The grammar deals with the standard spoken Sanskrit of Pāṇini’s era—a stage between Vedic and classical Sanskrit; syntactically it is as good as being identical with the languages of the Brāhmaṇa and the sūtras. Its method and content build upon prior works on phonetics, phonology, and morphology that had grown out of work on codifying complex Vedic rituals in the concise sūtra format.

the excellence achieved must be interpreted as the culmination of a very rich grammatical tradition

The phonetic treatises had been developed to help fix the pronunciation of Vedic texts. They classify vowels and consonants by a single unified set of place features, crossed with a multi-valued aperture feature that distinguishes consonants from vowels, height within vowels, and stops from fricatives within consonants. Each place has a characteristic resonance (dhvani), activated by tone (nāda) if the throat aperture is closed, and by nose (śvāsa) if it is open, producing respectively voice (ghoṣa) and voicelessness (aghoṣa). Increased airflow (vāyu) produces aspiration. High pitch (udātta) is ascribed to tenseness of the articulatory organs, resulting in the constriction of the glottis (kaṇṭhābila); low pitch (anudātta) from relaxation of articulatory effort with consequent widening of the glottis. The grammar presupposes phonetic categories and refers to them, but imposes its own phonological classification on sounds based on how they pattern in Sanskrit. In phonology, Pāṇini’s work was preceded by the construction of word-by-word (padapāṭha) versions of Vedic texts, and the formulation of rules for converting these man-made texts back to their orally recited originals in which the words fuse together by the rules of sandhi. The breaking down of sentences into words and their substitution rules to reconstitute the running text reveal considerable grammatical sophistication, showing that the extant padapāṭhas were completed when grammar had already reached an advanced stage. In morphology, Pāṇini drew on the fundamental idea that words are composed of meaningful parts, which appears in Vedic exegesis from the earliest prose (the Brāhmaṇa).

An Overview of the achievements of the Aṣṭādhyāyı̄

Pāṇini’s achievement was to formalise and extend these initiatives in a vastly more ambitious undertaking: a grammar of the entire language that relates sound and meaning, through rules for building words and sentences from their minimal parts. It was not quite intended to be a practical reference grammar, still less a textbook. Simplified and abridged works suitable for these purposes were produced later. It sought solely to extract all grammatical regularities, rigorously guided by the twin imperatives of complete coverage, and the principle of Minimum Description Length. The latter requires the grammar to be the shortest overall representation of the data, crucially including the principles and abbreviatory conventions through which data is encoded.

The Aṣṭādhyāyı̄ is a grammar with the goal of systematically analysing correct sentences of Sanskrit, not only of classical Sanskrit but also of the Vedic version. The analysis is realised by first identifying the constituents of the words of a sentence and then subjecting them to an analysis in terms of bases, affixes and operations relative to the emergent structures. It is to be noted that the emergent structures are an imagination of the grammarian, and do not exist outside the world of grammar [30], but the objects of the analysis are real. For this reason, Leonard Bloomfield [3] calls the Aṣṭādhyāyı̄ “one of the greatest monuments of human intelligence”. He adds, “It should be remembered, however, that the excellence achieved must be interpreted as the culmination of a very rich grammatical tradition”.

Pāṇini’s grammar serves as a means towards understanding sentences. This goal is accomplished by abstracting generalisations from usage, and formulating rules which best capture that usage. In order to facilitate proper formulation, interpretation and application of rules, the grammar requires a meta-theory that is brilliantly provided by Pāṇini. Through the meta-theory, he succinctly defines terms, sets forth rules of interpretation and outlines conventions he follows. In the sūtra style, one must make inferences, test and reject or accept them depending on whether or not they are in consonance with the Pāṇinian practice. In a sense, this could perhaps be interpreted as “extensible grammars” in the area of programming languages.

Pāṇini’s Rationale

Pāṇini’s rules of grammar rely on two simple concepts:

• that all nouns are derived from verbs, and
• that all word derivation takes place through suffixes.

However, Pāṇini does depart from these guidelines in some instances. He collected and incorporated words that did not conform to verbal derivation into a separate list. Such words “were often forcibly derived from verbal roots by means of a number of special suffixes. Pāṇini refers to all such words as ready-made stems, the formation of which does not concern him” (see [17]). To the extent that the Aṣṭādhyāyı̄ addresses word meanings, Pāṇini also chooses to accept the dictates of `common usage over those of strict derivation’. The grammarian says “that the authority of the popular usage of words… must supersede the authority of the meaning dependent on derivation. The meanings of words (the relations between word and meaning) are also established by popular usage” (see [17]). Pāṇini’s preference for examining the language as it was truly spoken, instead of adhering completely to intellectually defined rules, exemplifies the innovation of his work.

Sage Patañjali⁷ is to be commended for presenting the basic theoretical issues related to the grammar of Pāṇini. His work, known as Mahābhāṣya, begins with the statement “atha śabdānuśāsanam”, i.e., the instruction about words; the words include those from the Vedic as well as classical Sanskrit literature. He first discusses “words” as the subject matter of grammar. Patañjali does not accept words merely as jāti (species), ākṛti (form), kriyā (action), or guṇa (attribute). For him, a word is that which when uttered brings about a comprehension of its meaning. A word is thus Dhvani but only for the common people. For grammarians, the real word is sphoṭa, “that by means of which meaning is made manifest. It is received by ears, perceived by Buddhi, the mind, thought-process and reflected in sound (Dhvani). Meaning does not leave a word. Meaning is comprehended by the word itself. The word is eternal and resides with us” (see [30]). The basic purpose of a grammar is to account for the words of a language, not by enumerating each one of them but by writing a set of general rules with related exceptions. These rules must be based on generalisations abstracted from usage for which the language learnt is the norm. Use of correct words brings merit. That is, word-by-word enumeration is not a good means of understanding words, understanding them by means of incorrect words is equally futile. The mass of incorrect words is overwhelming and making generalisations based upon them is impossible. Hence, Patañjali recommends that for economy, one must study words by focusing on correct usage; again, a notion of grammatical inference plays a role.

The Pāṇinian Grammar Structure

Pāṇini’s grammar seeks to provide a complete, maximally concise and theoretically consistent analysis of Sanskrit that includes the spoken version, the Vedic version as well as regional variants then prevailing. It has optional rules [19] that distinguish preferable and marginal forms, and a few rules even have socio-linguistic conditions. In other words, variants are simply treated as alternate forms. Pāṇini’s grammar is hierarchical and with the following layers (i) sounds to symbolic phonemes, (ii) phonemes to meaningful morphemes, (iii) morphemes to syntactically well-formed words, and (iv) sentences. The grammar includes a good amount of implicit semantics through its linguistic content, and a set of basic semantic categories (available as databases). As a whole, the Aṣṭādhyāyı̄ consists of four components[32]:

1. Aṣṭādhyāyı̄: there are 4000 sutras in which 3983 are specially in kāśikāvṛtti (a commentary). It has eight chapters or adhyāyas,⁸ divided into 4 pādas. A sūtra or rule is referenced as x.x.x (x adhyāya, x pāda, x sūtra). For example, sūtra 1.1.1 (vṛiddhirādaic) refers to adhyāya one, pāda one and sūtra one.
2. Śivasūtra: the inventory of classes of segments (Sanskrit phonemes) partitioned by markers to allow abbreviations for classes of segments to be formed through additional techniques (pratyāhāras). There are 14 (Māheśvara sūtras) which work as data to enunciate any word.
3. Dhātupāṭha: the list has 1967 verb roots, and if the kaṇḍvādi roots are included then it becomes 2014, with subclassification and encoding of their morphological and syntactic properties.
4. Gaṇapāṭha: an inventory of classes of lexical items (or nominal stems) idiosyncratically subject to various rules. These contain other pertinent items like primitive’s nominal bases and avyayas.

The rules of the Aṣṭādhyāyı̄ make reference to classes on the elements in the other components by means of conventions spelled out in the Aṣṭādhyāyı̄ itself. Thus, while none of the components is intelligible in isolation, together they constitute a complete integrated system of grammar. The rules can be divided into four types:

1. Definitions that introduce the technical terms of the grammar.
2. Metarules that constrain the application of other rules throughout the grammar.
3. Headings supply a common element for a group of rules. A heading must be read into every rule in the domain over which it is valid unless it is semantically incompatible with its wording; they can stretch over 1000 rules in some situations dividing it into topical sections.
4. Operational rules are the workhorses of the system and are subject to applicable definitions, metarules, and headings. They carry out four basic types of operations on strings:
   1. Replacement
   2. Affixation
   3. Augmentation
   4. Compounding

In the following, we shall discuss mostly how the “replacement” rules relate to the generative capacity of contextualised replacement systems.

Forms of Rewrite Rules used by Pāṇini

The substitution rules envisaged in the Aṣṭādhyāyı̄ are precise and worth comparing to modern forms of substitution used widely in programming languages. Rules of substitution or replacement are prescribed using the left- and right- contexts. We generally follow the general structures described in [32],[19]. There are also other approaches like simulating the Pāṇinian system [25], or comparing with formal grammars like adjunct grammars [1].

a. Substitution: To describe the rule in Sanskrit that i is replaced by b when it is followed by a vowel, the process is:

\[\begin{align*}[i \rightarrow b] \text{ vowel}\end{align*}\]where i and b are terminals and the vowel is a non-terminal.⁹ Here, the context is marked by brackets. In general, when a rule states that b is replaced by c in context a ~-~ d, it is denoted by abd \rightarrow acd or

\(\begin{align}a[b\rightarrow c]d \end{align}\) where b is always a single element.

1. If at least one of a or d is not null, then the rule is referred to as context-sensitive.
2. If both the contexts (left- and right-) are null, then the rule is called context-free.
3. If the grammar consists of at least one context-sensitive rule, then the grammar is called context-sensitive grammar.
4. If the grammar consists of only context-free rules, then it is called context-free grammar.

Typical reference of case endings by Pāṇini (cf. [32]) looks like,

\[\begin{align}a + \text{ablative}, b + \text{genitive}, c + \text{nominative}, d + \text{locative}\end{align}\]

where + denotes a contextual concatenation operator.

One has to observe that

1. (2) corresponds to (1) but the order of elements in (2) is not fixed since their function is fully circumscribed by the case endings.¹⁰
2. On the other hand in (1), the order is fixed.
3. The differences between (1) and (2) reflect the differences between inflected languages and uninflected languages.

b. Recurrence: One of the methodological devices used by Pāṇini is “recurrence”. This principle is used to avoid a recurrent element or a string. This demands an ordering of the rules. The rules like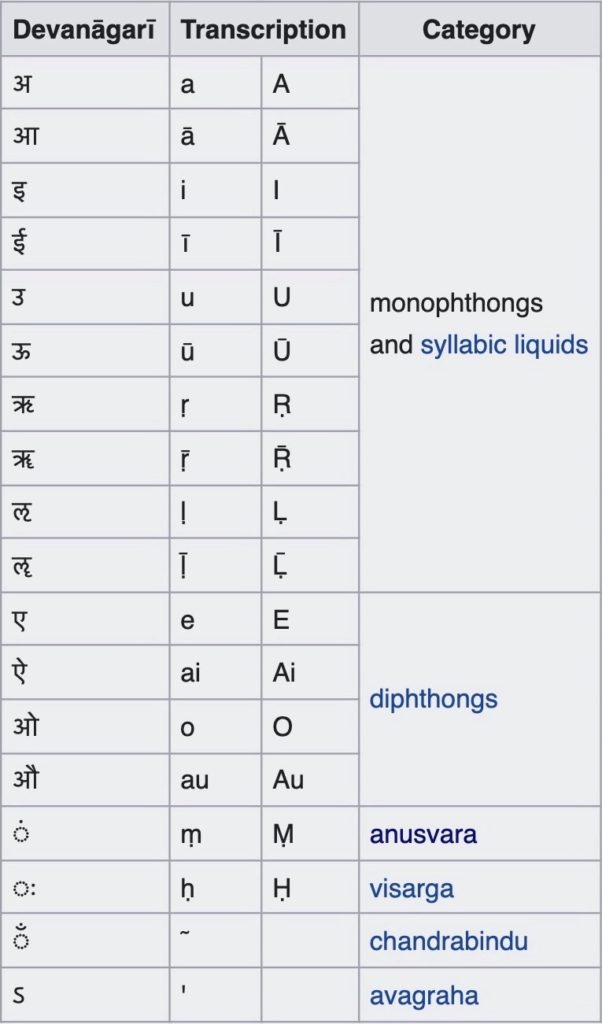

\[a_1[b_1 \rightarrow c_1]d_1\]

\[a_1[b_2 \rightarrow c_2]d_2\]

are replaced by Pāṇini by the following rules

\[a_1[b_1 \rightarrow c_1]d_1\]

\[~~~~[b_2 \rightarrow c_2]d_2\]

Here, in the second rule there is recurrence (called anuvṛtti) and may be expanded whenever necessary as:

\[(a_1)[b_2 \rightarrow c_2]d_2\]

The use of recurrence may be extended over numerous rules which need not all occur simultaneously. Ambiguity is therefore not excluded. However, Pāṇini assures consistency.

c. Useful simplification: The notation can be simplified by listing elements and referring to these in their respective order in the list. For example, Pāṇini replaces the following set of rules:

\[ a_1[b_1 \rightarrow c_1]d_1, …, a_1[b_n \rightarrow c_n]d_1\]

by the following single rule: a_1[b_1 b_2 … b_n \rightarrow c_1 … c_n]d_1

This is written in a matrix-like form shown below:
\[ a_1\left[
\begin{array}{ccc}
\left(
\begin{array}{c}
b_1 \\
\cdot \\
\cdot \\
\cdot \\
b_n \\
\end{array}
\right) & \begin{array}{c}\!\!\!\! \rightarrow\!\!\!\!\\ \end{array} & \left(
\begin{array}{c}
c_1 \\
\cdot \\
\cdot \\
\cdot \\
c_n \\
\end{array}
\right)\\
\end{array}
\right]d_1 \]

From the above elucidation, we can say that:

1. The grammar relies on the method of auxiliary markers, or terminal and non-terminal symbols, as the primary heuristic for expressing formal rules. Pāṇinian rules are defined using a semi-formal metalanguage for defining linguistic categories and rules which operate on those categories to generate Sanskrit expressions.
2. It is easy to see that the rewrite rules cover Chomskian rules considering that the element being replaced could also be \epsilon (meaning “empty” word—the identity in the concatenating world). In other words, the length of the right-hand side need not preserve the length of the left-hand side (the condition leads to context-sensitive grammars). From such a structure, we can see that Pāṇinian grammar can generate phrase structure grammars.
3. From the structure of the rules, one can visualise matrix grammars, ordered grammars, parallel rewriting systems etc (see [27] for details).

Remarks:
1. The user of the grammar will start with some Sanskrit target word, compound word or sentence in mind as the goal, and the Pāṇinian grammar works as a constructive generating device; that is, it is a derivational word-generating device. In general, it is not capable of `testing membership’ of the given expressions for grammatical correctness, though invalid derivations will at some point fail. In other words, there is no master definition of `grammatical expression’. An expression qualifies as grammatical just in case it can be produced by the rules. Further, the rules are non-deterministic, having several possibilities such as putting a sentence into an active or passive voice. Such a non-deterministic formulation further compacts the grammar and reduces its size for memorisation. As a means of better characterising empirical speech, Pāṇini also marks variant usage as occurring `usually’ versus `rarely’, or `sometimes’.

2. Bhartṛhari’s Vākyapadı̄ya was the work in which the speculations of the Indian grammarians found their fullest expression. One of the important notions of “Akanksha” literally means “expectancy”; it is a syntactic notion used to describe the following concept: words or phrases of different sorts have expectancy for words or phrases of other sort. If such expectancy is satisfied, a sentence results. Such a concept was developed in the “Mı̄māmsa” philosophy of the language. Its application is based on the syntactic work of Pāṇini. Bhartṛhari uses it in his discussions of treating the nature of a sentence as a sequence of words.

It must, however, be noted, as these formulations were prior to the “formal notions of computing” articulated by Post-Church-Turing, in the Aṣṭādhyāyı̄ one is not able to see notions of universal computations. Kadvany [17] relates the Pāṇinian approach through Post production systems and thus provides a succinct comparison with universal computation.

Pāṇini vs metasyntax of programming languages

The Backus-Naur Form (BNF) is a metasyntax notation discovered by John Backus and Peter Naur for describing the syntax of programming language ALGOL in their ALGOL 60 report. The notation is widely used to describe the syntax of programming languages, and quite often used to describe document formats, instruction sets and communication protocols. Such a description provides a precise and concise description of the language and allows recognition of possible structural ambiguities with simple constraints that lead to deterministic processing of commands or assert the declarative intent of the sentences.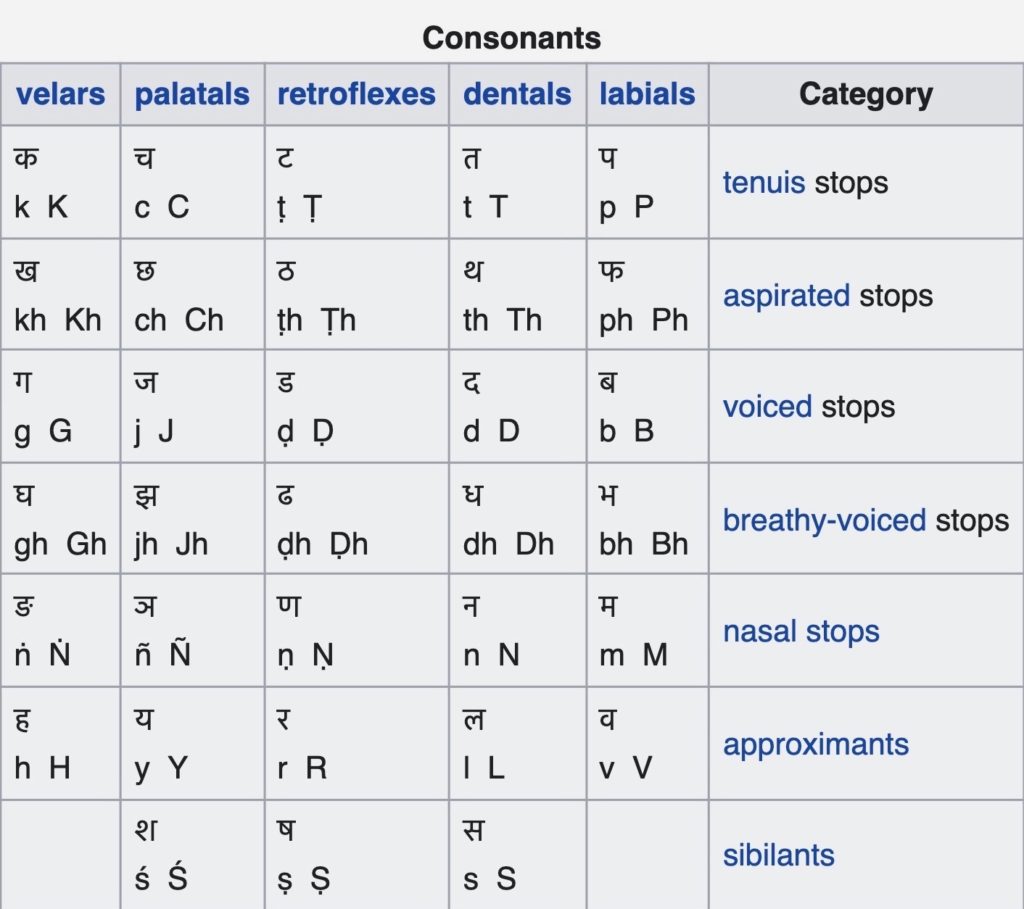

A succinct comparison of the BNF notation with the notations used in Pāṇini’s grammar has been captured by Ingerman [16]. The relation as envisaged by him is given below almost in his own words: “In order to describe the (rather complicated) rules of the grammar, he (Pāṇini) invented a notation which is equivalent in power to that of Backus and has a very similar property: given the usage to which the notation was put, it is possible to identify structures equivalent to the Backus “ | ”, and to the use of meta brackets “ < ” and “ > ” enclosing suggestive names. Pāṇini avoided the use of “::=” by writing the meta-result on the right rather than left as has been used even in other specification of syntax directed translations.”

The power of Pāṇinian grammar to express context-free grammars—a part of the modern families of formal languages—was first recognised by Noam Chomsky who refers to these grammars as precursors to his generative grammars that have widely come to be known as Chomsky grammars.

Commenting on the above, P.F. Ingerman further says: “Since it is traditional in professional circles to give credit where it is due, and as there is clear evidence that Pāṇini was the earlier independent inventor of the notation, may I suggest the name `Pāṇini-Backus Form’ as being a more desirable one?” It is of interest to quote Evelyn Lamb [21].

A comparison of Pāṇinian Grammar with Universal Computation

Kadvany [17], relates Pāṇinian structural rules with that of Post-Normal systems and relates the same with modern computation of Post’s canonical rules of the form gX \rightarrow Xh, where X is a variable symbol, and g and h are fixed strings.

Post’s methods show, for example, that axiom systems with rules such as {A, if A then B} \rightarrow B, can also be reproduced in rewrite form, with Post himself noting applicability to Russell and Whitehead’s Principia Mathematica. Using his canonical form for rewrite systems, Post demonstrated that his production/rewrite systems are equivalent to the representational power of Turing machines by showing that his standardised rules can be used to enumerate all rewrite rules and their productions. But for the use of spoken phonemes rather than inscripted graphemes, Pāṇinian methods can also be used to represent any target language according to Post’s theorems, and thus, capable of expressing universal computation through a largely direct application of the grammar’s rule system.

Kadvany nicely argues that: (a) similar to a modern computing language Pāṇinian grammar has a systematic method for introducing new symbolic categories and rules applying to those categories; (b) It is not as if Pāṇini devised a single ad-hoc rewrite system of ambiguous generality; (c) Pāṇini completed the difficult metalinguistic work needed to lay the groundwork for universal computation through the Aṣṭādhyāyı̄ as his grammar, described through the grammar’s metalanguage.

Thus Pāṇini is actually close to formulating a computing paradigm, given his generic and rigorous formulation of context-sensitive rules, that was formalized two and half millenniums later.

Māheśvara Sūtrāṇi (Śivasūtra)

Although Pāṇini’s Aṣṭādhyāyı̄ is the earliest work on Sanskrit grammar that has come down to us in full, unmodified form, Vedic scholars who preceded him had already worked out a sophisticated theory of phonetics to help fix the pronunciation of the earliest texts such as the Ṛgveda. They classified speech sounds by their place of articulation and degree of aperture of the mouth and larynx, as shown in Figure A.

Pāṇini organised the Sanskrit sounds in a particular way, letting them refer to certain groups of letters succinctly, in a series of 14 aphorisms believed to be a revelation from the drum beats of Śiva. For that reason, these rules are popularly called the Śivasūtra (also referred to as Māheśvara sūtrāṇi). Pāṇini also rearranged the alphabet—occasionally in less than intuitive ways—so that classes of sounds that combine in the same way with each other are adjacent. It is not as if one can define every group of letters with these sūtras, but one can define the most important ones.

Note that from top to bottom in the “two-dimensional” listing of consonants of the Sanskrit alphabet, the point of articulation moves outward in the oral cavity. For example, the first row of stops originates from the throat (the velars or gutturals), the second row from the soft palate (the palatals), and so on until the fifth row, which originates from the lips (the labials). Along the horizontal axis, the stops are organised according to increasing aperture, which correlates with increasing sonority or amplitude.

The vertical columns also reflect phonetic features implemented by constricting the larynx and oral cavity to manipulate the airflow, such as voicing (meaning vibration of the vocal cords) and aspiration. Remarkably, the vowels can also be classified by the same system.

The richness of the notation created by Pāṇini can be discerned from the 14 aphorisms of the Śivasūtra.

The Sanskrit Alphabet and its organisation

Let us reflect briefly on the elements of the Sanskrit alphabet and the syllables, which begin with the svaras or vowels, and then are listed the vyañjanas or the consonants. Vowels are sounds that are produced by letting air flow cleanly through the mouth (e.g., “a” or “o”. The airstream has no stops or breaks of any kind). Consonants, are sounds that are produced by interrupting the flow of air through the mouth (e.g., “ca”, “ba”). Below is a brief on some of the features.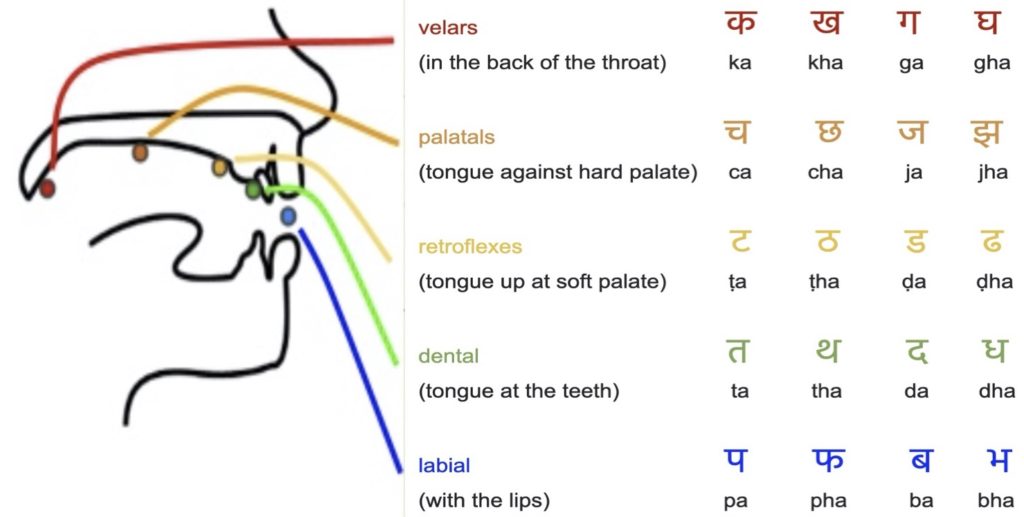

Vowels:

1. Short vowels: a (pronounced at the soft palate), i, u, ṛ.
2. Long vowels (pronounced for exactly twice as long as the short vowels): ā,ı̄, ū, ṝ.
3. Simple vowels: union of short and long vowels.
4. Compound vowels: combinations of two simple vowels and are pronounced for exactly twice as long as the short vowels.
5. Other classification of vowels: (i) weak: weak vowels are the simple vowels; (ii) medium: by adding an “a” sound to the front of the weak vowels, we get medium vowels; (iii) strong: by strengthening the “a” sound in a medium vowel, we get strong vowels; (iv) In Sanskrit, vowels oscillate, either as long or short vowels, from guttural (a, ā), palatal (i, ı̄), retroflex (ṛ, ṝ) and dental (ḷ, ḹ ) to labial (u, ū). The umlauts or the vowel mutations (e, ai, o, au) are always long.

Consonants:

1. Consonants are produced by interrupting the air flow. We can interrupt the air flow in one of three ways: (i) stopping it entirely, (ii) redirecting it (through the nose), and (iii) suppressing it, without stopping it entirely.
2. Soft palate consonants: we stop the air at the soft palate using the base of the tongue (ka, ṅa).
3. Hard palate consonants: we stop the air at the hard palate using the middle of the tongue (ca, ña).
4. Retroflex consonants: behind-the-bony-bump-on-the-roof-of-the-mouth consonants are long and hard to read (ṭa, ṇa).
5. Tooth consonants: we stop the air at the base of the top row of teeth using the tip of the tongue (ta, na).
6. Lip consonants: we stop the air with the lips and we don’t use the tongue at all (pa, ma).
7. Semi-vowels: consonants in this group are halfway between vowels and consonants. Like the vowels, the semi-vowels are voiced and unaspirated, produced by continuous air flow out of the mouth. We produce these sounds by suppressing the flow of air at the point of pronunciation (ya, ra, la, va).
8. “s”-sounds: hissing sound types are produced by suppressing the flow of air at the point of pronunciation; these are unvoiced, each having a different point of pronunciation: śa uses the hard palate, ṣa is a retroflex consonant, and sa uses the teeth.
9. Two sounds aṃ and aḥ: these are neither vowels nor quite consonants and appear only after vowels; they are called anusvāra and visarga respectively.

Syllables: The sounds of a language are arranged into packets called syllables, which are pieces of sound that have exactly one vowel. The syllable relies on the vowel to be pronounced.

1. A syllable must have a vowel, and it must have only one vowel. For example:
   • Syllables: a, ā, ki, ye, o, ghai, au
   • Not syllables: k, r, y, l
2. When the anusvāra or visarga appears, it ends the syllable. For example:
   • Syllables: aṃ, kaṃ, kāṃ, aḥ, kaḥ, kāḥ
   • Not syllables: ṃa, ḥa
3. A syllable must always start with a consonant. However, a syllable can start with a vowel only if one of the following conditions holds:
   • The syllable is at the beginning of a line.
   • The syllable follows a consonant that is removed due to a special rule.

Returning to Pāṇini’s Aṣṭādhyāyı̄, one observes that he adds extra letters to a term to show its properties. These letters only have a meaning in technical literature, and they never appear in the Sanskrit language. For that reason, such a letter is called anubandha, literally meaning “bound after”. In the listing given in the Śivasūtra table, all of the red letters are anubandha letters.

Illustrative Example: Choose a regular letter and attach an anubandha to it. The combination of a letter and its anubandha, called a pratyāhāra, indicates everything from the letter to the anubandha. It means that we can create hundreds of different groups of letters by just naming the two.

For example, the word ac refers to all of the vowels. This pratyāhāra consists of two parts: a, which is the first letter in line 1, and c, which is the anubandha in line 4. As another example, the word hal refers to all of the consonants. This pratyāhāra consists of two parts: ha, which is the first letter in line 5, and l, which is the anubandha in line 14. Note that the a in ha is just there to make the word easier to pronounce. Pāṇini never uses pratyāhāra to refer to sets consisting of a single phoneme.

Note also that the anubandha letters are all quite rare in Sanskrit. Through the choice of using rarer letters, Pāṇini could reduce the chance that a pratyāhāra could be mistaken for a real word. Some of the odd aspects of the rules are:

1. ha is included twice! The second ha can only form a pratyāhāra with the l in its row, producing hal. But this second ha is never used to define a pratyāhāra. Instead, it is used within other pratyāhāras. For example, śa includes all of the sounds in śavarga, which includes ha.
2. What about four long vowels? It is true that the four long pure vowels (ā, ı̄,ū, ṝ) are all missing, even though all these are counted with their short counterparts. So, the pratyāhāra ac includes all of the pure vowels: a, ā, i, ı̄, u, ū and ṛ. Note that the long form ṝ, unlike the short form ṛ, never occurs as an independent letter in any word. For example, ṛ occurs in the word Ṛgveda; whereas ṝ occurs only in half-forms, adjoined with another letter, like in the words mātṝṇām or pitṝṇām.
3. ṇ is used twice as an anubandha! This is a real ambiguity. It is possible that Pāṇini ran out of anubandha letters and was forced to be ambiguous here. Unfortunately, you’ll have to rely on the context of a rule to interpret a word using the ṇ anubandha.

From these 14 aphorisms, a total of 281 pratyāhāras can be formed:
(14\cdot 3)+ (13\cdot 2) + (12\cdot 2) + (11\cdot 2) + (10\cdot 4) + (9\cdot 1) + (8\cdot 5) + (7\cdot 2) + (6\cdot 3 )+ (5\cdot 5) + (4\cdot 8) + (3\cdot 2)+ + (2\cdot 3) +(1\cdot 1), (where \cdot signifies multiplication), minus 14 (as Pāṇini does not use single element pratyāhāra) minus 10 (as there are ten duplicate sets due to h appearing twice); the second multiplier in each term represents the number of phonemes in each. But Pāṇini uses only 41 pratyāhāras (with a 42nd introduced by later grammarians) in the Aṣṭādhyāyı̄.

The Śivasūtra places phonemes with a similar manner of articulation together, such as sibilants in line 13 (śa ṣa sa R) or nasals in line 7 (ña ma ṅa ṇa na) M. Economy (referred to as lāghava in Sanskrit) is a major principle of their organisation, and it is debated whether Pāṇini deliberately encoded phonological patterns in them (as they were treated in traditional phonetic texts called Prātiśakhyas) or simply grouped together phonemes which he needed to refer to in the Aṣṭādhyāyı̄ and which only secondarily reflect phonological patterns (as argued in [19] and [29]). Pāṇini does not use the Śivasūtra to refer to homorganic stops (stop consonants produced at the same place of articulation), but rather the anubandha U: to refer to the palatals c ch j jh, Pāṇini uses cU.

Pāṇini uses a significant set of rules of transformation. As an illustrative example, consider the rule 6.1.77 in the Aṣṭādhyāyı̄: iKaḥ yaṆ aCi.

iK means i u ṛ ḷ;

iKaḥ is iK in the genitive case, which means ‘in place of i u ṛ ḷ’;

yaṆ means the semi-vowels y v r l and is in the nominative, so iKaḥ yaṆ means `y v r l replace i u ṛ ḷ’.

aC means all vowels, as noted above

aCi is in the locative case, so it means before any vowel.

Hence, this rule replaces a vowel with its corresponding semi-vowel when followed by any vowel, and that is why dadhi together with atra makes dadhyatra. The proper pairings i\rightarrow y,~ u\rightarrow v, ṛ \rightarrow r,~ ḷ \rightarrow l (rather than, say i \rightarrow r) are ensured by a further general condition: among alternative possible replacements which the rule allows are precisely, y for i, v for u, r for ṛ, and l for ḷ as desired.

As shown already, Pāṇini uses in Śivasūtra, a table which defines the natural classes of phonological segments in Sanskrit by intervals.

Petersen [29] presents a formal argument showing that Pāṇini’s representation method of ordering the phonological segments to represent the natural classes is optimal. The argument is based on a strictly set-theoretical point of view depending only on the set of natural classes and does not explicitly take into account the phonological features of the segments which are, however, implicitly given in the way a language clusters its phonological inventory. The key idea is to link the graph of the Hasse diagram¹¹ of the set of natural classes closed under intersection to Śivasūtra style representations of the classes. Towards forming Śivasūtra like alphabet, he formally defines S-alphabet and establishes results that say that Pāṇini’s method of representing hierarchical information in a linear form is an interesting field for further investigation. Especially, the fact that this method enables one to define phonological classes without referring to phonological features is remarkable.

Sanskrit sounds written according to the International Alphabet of Sanskrit Transliteration (IAST) are based on Pāṇini’s organisation of the language. The points of articulation of the moves outward in the oral cavity, and the consonant stops are organised according to increasing aperture, which correlates with increasing sonority or amplitude.¹²

Discovering Computing Processes in the Aṣṭādhyāyı̄

In an earlier section, we described how Kadvany [17] has compared Pāṇinian systems with universal computation through Post systems. Here, we highlight how he demonstrates that the language can be extended or bootstrapped.

From the Kāraka theory, one can see a process of enriching the existing grammar through additional rules. To construct such a new version of the grammar, one might introduce a Kāraka rule which, by some new affixing marker, segregates numerical or computing terms from ordinary Sanskrit grammar. Derivations starting from this new starting point would be isolated from the original grammar. Categorical definitions, for `numbers’, `constants’, `variables’, `addition’, `multiplication’ and other logical and computing categories would need to be introduced using Pāṇinian style rules. These could involve simple recursive definitions typical of computing syntax for categories such as `formulas’, `sentences’, `proofs’ and `theorems’. Applying to such categories, just as with a modern formalism, rules for new derivations could be cast as replacement rules of many kinds, including the context-sensitive rules described earlier.

Thus, the expression of computations using Pāṇinian grammar can almost be just a transcription of a modern formalism into the grammar, enabled by its native technique for categorical and rule definitions. To quote Kadvany,

The parallel between a modern computing language, or formalism, and Pāṇinian grammar can be thought of in terms of its four major functional components: (1) the rewrite formalism by which Sanskrit expressions are ultimately constructed; (2) the metalinguistic paribhāṣa rules guiding those operations; (3) the finite inventory of phonemes, stems and roots to which rules initially apply; and (4) the versified sūtra codifying all rules in reduced form. As highlighted by Kadvany,

Reflecting on some of these highlighted aspects from the modern standpoint of computing, of making connections with a work from two and a half millennia older time-scale, is it good to project contemporary mathematical ideas into its distant history?

While it may not be fair to attribute the understanding of the advanced formal methods of computing to the Pāṇinian system, it certainly shows the maturity with which the notations were devised to arrive at a succinct form to articulate preferred sentences, both in their oral and written forms. The notions of calculation or computation have evolved in the course of time, and we now have Alexa and Siri, which try to construct reasonable phrases or sentences wherein we can recognise the ubiquity of Pāṇinian thinking in its own way.

We can say for certain that Pāṇini invented rewrite methods that were rediscovered more than 2000 years later, perhaps with a different objective. Glimpses of Pāṇini’s inferences through rules and finite set of databases of root verbs, stems, phonemes in arriving at phrases and sentences that were prevalent in the society both in the oral and the written form, are indeed reflected in the current day language translators or question-answering systems using natural-language technology that are becoming ubiquitous.

Kāraka Theory and Knowledge Representation

Knowledge representation plays a crucial role in the computer understanding of natural languages or artificial intelligence in general. Briggs argues (cf. [4]) that the Pāṇinian approach of language analysis parallels that of knowledge representation used in artificial intelligence. Before briefing his approach, let us take a look at the Kāraka theory of Pāṇinian grammars.

An overview of the Kāraka Theory

The classical Pāṇinian approach facilitates the task of obtaining the semantics through the syntactical framework. In text summarisation, human cognition focuses upon the identification and interpretation of important sentences that is broadly known as Śabdabodha. This theory tries to acquire a verbal knowledge through the application of the Kāraka theory. An extensive and perfect interpretation of phonology, morphology, syntax and semantics is available in Pāṇinian grammar. It ideally explores all the concepts of theories of scientific analysis and description of a language. The Pāṇinian approach focuses on information while analysing language structures. It analyses the language from both the communicator’s and recipient’s points of view. During communication between them, the information is coded in the language strings. While analysing these language strings one is expected to decode such information.

it is clear that the Pāṇinian grammar is sentence-based and not merely word-based.

From a cognitive perspective (cf. [2]), the recipient understands the entire sentence first and then concentrates on the meaning of the individual words. Thus, the analysis can be understood in two stages (i) syntax and (ii) morphology. The Pāṇinian framework considers that the words and sentences are isolated and thus, only when they come in a group through a formal process, they contribute to the overall meaning of the sentences. Since Pāṇini accepts the existence of words only within the sentences, it is clear that the Pāṇinian grammar is sentence-based and not merely word-based. During sentence analysis, the Pāṇinian approach does not propose any separate syntactic level. Instead, it assumes various levels of sentence analysis for the actual written or spoken sentence for its interpretation. Each level in this analysis is more refined than the previous one. The first one is the actual string or the sentence, and the second one represents the communicator’s actual intention, i.e., the real thought behind the sentence. The early level known as Vyākaraṇa makes minimal use of world knowledge and uses mostly morphological knowledge. The later levels make greater use of the knowledge of the world or semantics.

The Pāṇinian framework considers two more crucial levels known as Kāraka and Vibhakti levels [2] in between the surface and the semantic levels. Note that even the surface level considers the notion of Vivakṣa, i.e., a speaker’s viewpoint to a certain extent, which has a relation to pragmatics. The surface level captures the written or the spoken sentences as it is. In between this surface level and the upper level, i.e., the Kāraka level, there exists the Vibhakti level, which is purely syntactic. At this level, the case endings are used to form the local groups of the words.

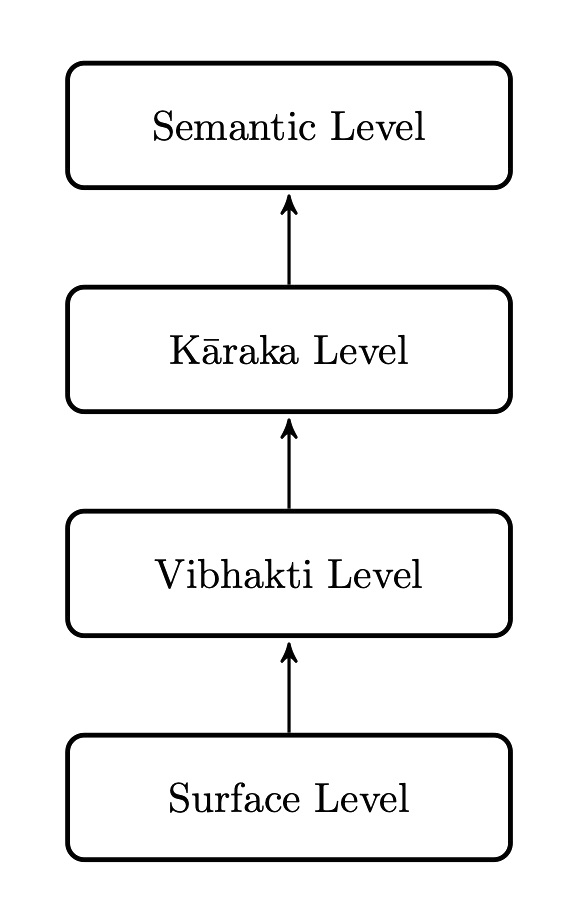
The word divisions are indicated in Figure C.

At the Vibhakti level, a noun group is formed containing a noun, which contains the instances of noun or pronoun etc. These instances are included with their respective Vibhaktis. According to Sanskrit grammar, Vibhakti is the word suffix, which helps to find out the participant’s gender, as well as the form of the word. Vibhakti for verbs includes the verb form and the auxiliary verbs. Vibhakti gives TAM (Tense Aspect Modality) details of the word. These labels are syntactic in nature, and are determined from the verbs or the auxiliary verbs. Hence Vibhakti plays an important role in Sanskrit.

After Vibhakti, the next Kāraka level, that is, the relation of the participant noun to the verb is determined. Contrary to Vibhakti, the Kāraka relations are Syntacto-semantic. These relations are established in between the verb and other constituent nouns that are present in the sentences.

Through these relations, the Kārakas try to capture the information from the semantics of the texts. Thus, the Kāraka level processes the semantics of the language but represents it at a syntactic level. Hence, it acts as a bridge between semantic and syntactic analysis of a language. In Pāṇinian grammar, the sentence analysis is carried out by considering the centrality of the verb. Here, the verb is considered as the binding element of the sentences. In Kāraka theory a sentence is defined with reference to Kriyā, i.e., action, Kāraka, i.e., participatory factor, and Anvaya, i.e., their relation. In summary, Kāraka is defined as that which follows action. In a sense, it is the relation between the noun and the verb. The derivational process is illustrated below.

Sanskrit is a free-order language and requires roots and stems that are user-selected. From this starting point, metalinguistic rules are used to mark roots and stems as having their intended syntactic roles, using six functional categories that today’s linguists may characterise as agent, goal, patient, instrument, location and source. Paul Kiparsky provides a succinct explanation as follows: Pāṇini’s grammar represents a sentence as a little drama consisting of an action with different participants, which are classified into role types, called Kāraka roles, or functions assigned to nominal expressions in relation to a verbal root. While such choices are made by the user, the Kāraka metarules list the categories and rules for using them. Pāṇini thus takes meanings into consideration from the very outset of a derivation (see [6] [p.160]). Because of that, and the need to interpret rules through a working knowledge of Sanskrit, the grammar is not sharply divided into phonology, morphology, syntax and semantics as in some modern linguistics (see [7] [p.14]).

Kadvany [17] provides an abstraction of the derivation process, and a comparison with forming a well-formed program in a computing language.

Let us look at an example of a sentence derivation (see [30][Ch.3]), as elucidated by Kadvany [17]: Suppose the goal is to derive a correct Sanskrit expression of Devadatta is cooking rice in a pot with firewood for Yajñadatta: devadattaḥ odanam yajñadattāya sthālyām kāṣṭhaiḥ pacati. The Kāraka roles chosen would be the verbal action of cooking, an agent Devadatta, a patient of the action which is rice, an instrument of firewood, a location of the pot, and a recipient Yajñadatta of the action. The Kāraka categories are formally defined and regulated by metarules, and provide a powerful heuristic for constructing a wide range of sentences. The categories mediate informal semantic meaning through their functional syntactic role. The free word-order of Sanskrit means the collection of initial stems, roots or words to associate with Kāraka roles can be thought of as an unordered set: {devadatta, firewood, rice, cooking, pot, yajñadatta}, i.e., devadatta, kāṣṭha, odana, pac, sthāli, yajñadatta. Again, as Kiparsky puts it, the grammar is a `pure form of lexicalism’.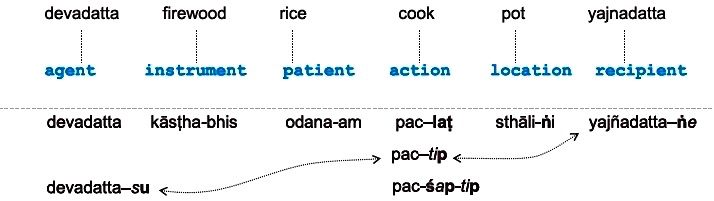

The elements, schematised in Figure D, require rule applications to mark their assigned Kāraka roles and to create new expressions. For example, the pot is singular and the location of the action, and is marked by the suffix –ṅi, producing sthāli-ṅi. The boldface ṅ represents an auxiliary and non-terminal marker used in the derivation process, with italicised i being a terminal sound, and the hyphen indicating concatenation. Similarly, yajñadatta is the recipient of the action, marked by the suffix—ṅe and yielding yajñadatta–ṅe. The patient and instrumental roles, for rice and firewood respectively, can be marked with suffixes not needing auxiliary markers: odana-am and kāsṭha-bhis. Derivation of the verb and its inflection for the cooking action, pac, involves more steps. The interested reader is referred to Kadvany [17] for further details.

Affixing and Bootstrapping

The derivation above is typical; that is, auxiliary markers are similarly used throughout the grammar for rule-expression and their application. Sanskrit syntax is highly governed by case endings, and thus, the approach of Pāṇini essentially extends the Sanskrit object language by its own means. The systematic role for affixing makes Pāṇini’s innovation a kind of grammatisation, which is often central to language change generally. Here, existing affixing resources of the object language, Sanskrit, are generalised to describe the object language itself.

In the theory of computation, the analogous bootstrapping innovation is to use Post-type rewrite rules to formulate a metarule, or system, for all rewrite rules; or to use Type 0 grammar to define a universal Turing machine; or, as shown by Gödel, to use number theory to define a metalanguage for its own derivation and so forth. Such bootstrapping also occurs practically when a programming language like C++ or Pascal is used to write its own compiler, with successive versions accommodating larger swaths of the language. The difference in the Pāṇinian approach arises as we assume the spoken natural language Sanskrit and its structure to begin with. The object language is neither a mathematical invention nor is it necessarily even written.

Knowledge Representation using Pāṇinian Grammar

In 1985, Rick Briggs [4] of the Research Institute for Advanced Computer Science of the NASA Ames Research Center argued that natural languages can serve as well as artificial languages for representing knowledge.

Using Sanskrit as an example of a natural language, he argues that Sanskrit grammarians had “a method for paraphrasing Sanskrit in a manner that is identical not only in essence but in form with current work in artificial intelligence”. He says that “one of the main differences between the Indian approach to language analysis and that of most of the current linguistic theories is that the analysis of the sentence was not based on a noun-phrase model with its attending binary parsing technique, but instead, on a conception that viewed the sentence as springing from the semantic message that the speaker wished to convey”.

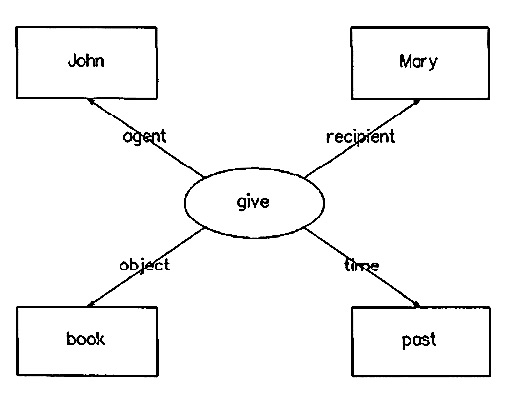
He lays out a typical Knowledge Representation Scheme (using `semantic nets’), and illustrates with an example through the method used by the ancient Indian grammarians to analyse sentences unambiguously.

A semantic net is a graphical representation of concepts in the world. It is essentially a directed graph, whose nodes represent individuals or concepts (like event, action names, objects, places, time etc.), and links (edges/arcs) are labelled to represent relationships between these concepts. An edge/arc/link is labelled by the name of the relationship it represents. Several arcs can have the same label. However, each node represents a single individual or concept. Such a representation denotes the meaning independent of the words used. The other idea is to eliminate the potential interference of syntax in understanding the meaning implied by the sentence. For example, the sentences, “John gave a book to Mary” and “Mary was given a book by John” are semantically the same though the syntax is different. So, if we take an example of an event as “John gave a book to Mary”, we get the following picture as a possible semantic net illustration. We refer to [4] for a more detailed discussion of this example.

One of the underlying reasons for Briggs’ argument can be understood by looking at the rationale of semantic specification of a natural language and the way Pāṇini generates correct sentences. Semantic specification of natural languages (specifically English) has been nicely articulated by Woods (cf. [33]):

Pāṇinian grammar, through its use of rule precedence and other meta-conventions, generates a single derivation for every grammatical sentence of Sanskrit. As pointed out in [27], “through the lens of contemporary natural-language processing, the most amazing fact about the Aṣṭādhyāyı̄ is not that it produces so many correct derivations after all, but that it simultaneously avoids so many incorrect ones.” These aspects shall become more pronounced if we relate Kāraka theory with the extended semantic network formalism of [11]. We shall illustrate such a relationship in the following informally; first we relate semantic networks and logic programs.

Representation of Semantic Networks as Relational or Logic Programs

Relationships of the network can be captured in what is known as Horn Clause Programming¹⁴ (cf. [22]) and can also be described using Horn clauses.

Coming back to semantic networks, simple semantic networks can only express collections of variable-free assertions. First, let us consider a simple generalisation before going for extended semantic network formalism to take into account representation of assertions with variables in an informal way.

In the semantic net illustration, relative to the Kāraka “give”, other “phrases” can be treated as place holders. That is, agent (give, ?), recipient (give, ?), Time (give, ?), and object (give, ?) where “?” denotes unknown. For such an interpretation, capturing the above relations in a logical formalism enables us to understand the embedded richness of the Kāraka theory of the Aṣṭādhyāyı̄. That is, the Kāraka theory effectively is making general propositions rather than simple assertions.

Thus, constants like John, book, past, and Mary can be treated as variables—say by replacing those by “?”. This is possible naturally in the logic programs as it satisfies the property of input/output invertibility. The generality through variable instantiations can be captured assuming a database of ground facts of the respective predicates. In Pāṇinian rules, an expression qualifies as grammatical just in case it can be produced by the rules. Further, the rules are non-deterministic, having several possibilities such as putting a sentence into an active or passive voice. As a means of better characterising empirical speech, Pāṇini also marks variant usage as occurring `usually’ versus `rarely’, or `sometimes’.

As highlighted in [17], it is also to be noted that in the Aṣṭādhyāyı̄, the context-sensitive conventions are used as a master format for sūtra coding, and hence are a consistent clue to their meaning. These aspects could perhaps be captured largely in the logical formalism using the notion of search rules like that exists in Prolog.

Generalisations through inferences that are part of logic programs, particularly through extended formalism of semantic networks, has been explored in [11].

As we create semantic nets for more complex networks, it results in a hierarchic structure of semantic nets, and the explicit set-relationships are essential to understand the meaning of the sentence and facilitate inference. It must, however, be noted that W.A. Woods, the original author of semantic nets, was more concerned with the semantics of the natural language and the representation of natural-language meanings than with semantics of semantic net formalism itself. To alleviate such issues, [11] proposed an extended formalism of semantic networks that allows a rich representation to visualise complex representations. A brief on the same is given below.

Extended Formalism and Kāraka Theory

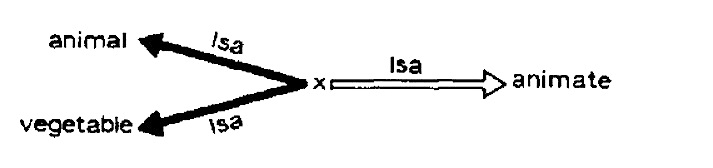
Assertions with variable and other extensions, taking into account inference/deduction, is realised through clausal form of logic. In the extended formalism, terms are denoted by nodes. Constants, variables, and functional terms are respectively represented by constant, variable and functional nodes. Binary predicate symbols are represented by labels along the arc, and atoms are represented by the arc label along with the two end-nodes. Direction of the arc indicates the order of the arguments of the predicate symbol that labels the arc. Conclusions and conditions are represented by different types of arcs: conditions are drawn with two lines and conclusions are drawn with bold lines.

In the following simple example of extended semantic network, the arc labelled “isa” with x and animate as left and right end-nodes is a condition, and the arc labelled “isa” with end-nodes x and animal is a conclusion. Thus, this illustrated semantic net represents: every animate is a vegetable or an animal.

In fact, the clause Act (t(x), take) \leftarrow (x, give) expresses that for every act of giving there is an act of taking. Knowledge representation that depicts the fact “that the actor of any act of taking is also the recipient of the action” is expressed by the extended network. For an assessment of its expressive power, the reader is referred to [11].

Relationship of Extended Semantic Network and Kāraka Theory: Though the concept of a semantic net as a way of representing knowledge was not available to the Sanskrit grammarians in the form discussed above, Briggs has shown the equivalence between their approach and semantic nets. Thus, the use of semantic nets could possibly show how the grammarians went about their formalism. Several dependencies among the components of a sentence are derived and depicted as a dependency graph in [10]. Such dependency graphs can be transformed into the extended semantic network formalism as discussed above. In other words, the extended formalism could be used as a model to understand how the Sanskrit grammarians could have arrived at such a succinct model for Sanskrit.

The power of extended semantic nets can also be seen through an example of a picture logic programming. In [24], Bernd Meyer proposes logic programming with picture terms to realise a visual formalism where picture terms can be considered as partially specified pictures. He explores picture logic programming through Picture Clause Grammars (PCGs). These are related to picture programs in the same way as Definite Clause Grammars [23] are related to normal Prolog programs. PCGs are more restrictive than arbitrary picture programs [24], i.e., they can only recognise a subclass of the pictures that can be recognised by picture programs. For purposes of illustration, consider the example depicted in Figure G, where circles are used for entities, diamonds for relationships and triangles for generalisations.

Syntactically, a diagram consists of a relation or a generalisation inside of a diagram. In fact, this could be under extended semantic nets. This also shows the power underlying the implicit knowledge representation used in Sanskrit grammars.

We remark that the extended formalism has the power of “inference” of logic. Such an interpretation also allows us to understand Pāṇini’s razor as articulated by Kiparsky [20] in a constructive way; it will surely provide clarity on “short grammar” or the roles of induction etc., in the Aṣṭādhyāyı̄.

Logic Formalism, Unification, Kāraka Theory and Knowledge presentation

Historically, a clean and powerful formalism for describing natural and artificial languages followed from a method for expressing grammars in logic due to Colmerauer [8] and Kowalski [11]. This formalism, which is a natural extension of context-free grammars, is often referred to as Definite Clause Grammars (DCGs). Since DCG is an executable program of the programming language Prolog, it provides not only a description of a language, but also an effective means for analysis. Pereira and Warren [28] compare DCGs with the successful and widely used Augmented Transition Network (ATN) formalism, and indicate how ATNs can be translated into DCGs. They further argue that DCGs can be at least as efficient as ATNs, whilst the DCG formalism is clearer, more concise and in practice more powerful. In the DCG formalism, unification (to be specific, it is MGU, standing for Most General Unifier) plays a crucial role for interpretation and computation.

Having interpreted Kāraka theory in terms of logic formalism, a natural question will arise about the relationship of “unification” as used in logic. The interested reader can take a look at the simple example illustrated in Figure H.

We have just discussed the relationship of Kāraka theory and the extended semantic network formalism. One needs to analyse the role of “unification”, which is vital in DCGs, from the perspective of Kāraka theory, as well as from the binding of rules and pragmatics. It is of interest to note that, historically, there exists a body of grammars referred to as “Unification-based approaches to grammar” [31] that are the result of separate research in computational linguistics, formal linguistics, and natural-language processing; related techniques can be found in theorem proving, knowledge representation research, and theory of data types.

Several independently initiated strains of research have converged on the idea of unification to control the flow of information. In fact, the relation between Kāraka theory and extended formalism of semantic networks provides a strong basis of the role of unification in Sanskrit, as it is a free-order language and the Aṣṭādhyāyı̄ has its own objectives of relevance to spoken and written forms of Sanskrit as already highlighted.

In fact, in this context, it is nice to observe some of the aspects articulated as “A Computational linguist’s wish-list” by Veronica Dahl [9]:

1. avoiding overgeneration,
2. obtaining semantic representations,
3. unbounded or long-distance dependency, for instance, Topicalization, and
4. using pragmatic knowledge to glean implied meaning.

As remarked by Kiparsky, note that overgeneration is avoided through the rules in the Aṣṭādhyāyı̄. The other aspects are captured to an extent required in Sanskrit, as reflected in the discussion on Kāraka theory and extended semantic net formalism.

From the discussions above on Kāraka theory, and the semantic formalism, how far Pāṇini overcomes other aspects is worth analysing in the Sanskrit language itself rather than transformational adaptation of Pāṇinian grammar for other languages and analysing for such characterizations. While the number of Sanskrit speakers is very small, it is indeed important that computing scientists and Sanskritists come together to understand these aspects. The gain of such a study would be enormous for understanding the beauty of Sanskrit as well as the pragmatic cognitive skills a human uses in understanding or mastering a natural language.

Pāṇini’s Razor

Kiparsky [20] makes a nice presentation comparing the notion of simplicity elucidated throughout in the Aṣṭādhyāyı̄, relative to the notions of Occam’s razor, Chomsky’s razor etc., and summarises Pāṇini’s razor, largely captured by the word lāghava as follows:

• The simplicity metric applies to the whole system: rules in the Aṣṭādhyāyı̄ for phonology and lexicon, like Śivasūtra, gaṇapāṭha and dhātupāṭha.
• The metalanguage (technical terms and certain conventions of rule application) is defined within the grammar itself.
• Shortest grammar = shortest theory.

Consequences of the above lead to:

• Abstract categories such as kārakas, lakāras,…;
• principles governing rule interaction: blocking (utsarga or apavāda), anuvṛtti, adhikāra and the siddha-principle;
• abbreviations for recurrent arbitrary classes: ghi, ghu, bha, ārdhadhātuka…

The inductive value of Pāṇini’s razor is captured by [17] as follows:

• The core categories of Pāṇini’s Sanskrit grammar recur in widely divergent languages.
• Principles like blocking (utsarga or apavāda, sāmānya/viśeṣa) and the siddha-principle.
• Arbitrary classes are grammatical realities (declensions, conjugations etc.).

From this, he concludes that a systematic application of the Pāṇinian razor to one language brings out concepts and principles that apply to other languages. This suggests that the Pāṇinian razor is a sound methodological basis for linguistics.

He further compares the paradigm to

• modern ideas on induction and algorithmic complexity like Minimum Description Length, Kolmogorov Complexity, and
• the hypothesis that a universal measure of algorithmic complexity is enough to explain properties of grammars.

He argues how Pāṇini’s razor leads to (1) induction, statistical prediction, and (2) data compression, Formal Concept Analysis.

Conclusions

It is hard to imagine that concepts that originated some 2500 years ago find a semblance with modern concepts whose environment is drastically different from that which existed so far back in time. Pāṇini’s Aṣṭādhyāyı̄ is one such gigantic incomparable work. It is not just the semblance but the generality, brevity and thoroughness one finds in the Aṣṭādhyāyı̄ that is astounding.

The aim of the article had been to relate the explicit and implicit computational thinking¹⁵ that Pāṇini had in articulating a grammar for the spoken and written Sanskrit. From a pure comparison perspective of the rewriting systems, as stated in [17], Pāṇini’s basic method was rediscovered in the 1920s and 1930s by Emil Post through his production/rewrite systems. Far-reaching aspects of equivalence could be discerned if we look back at the origin of “algorithm” in the early 20th century. The famous logician Alonzo Church, through \lambda-definability, had come up with the notion of “effective computability”. However, this was thoroughly unsatisfactory to another famous logician Kurt Gödel. Alan Turing’s submission of his famous work in 1936 that heralded the notion of “algorithm” is evident in the review by Alonzo Church of the contemporary works on effective computability. According to Church:

The Turing machine became the founding abstraction of digital computers instead of the other formalisms even though they existed earlier. Once the relations among these abstractions were established, the other formalisms too found their way into computing in several ways. In the same way, one needs to understand that Pāṇini’s formalism has no direct bearing on the content of mathematical algorithms. However, as the sūtras get encoded using the current day formalisms, they create shared space for computation, formal description and Sanskrit as a natural language.¹⁶

In this article, we have tried to discuss various works that relate Pāṇini’s work with respect to formal grammar formalism, logic formalism, Kāraka theory, knowledge representation and so on. The confluence of linguistic and mathematical thoughts in Pāṇini’s Aṣṭādhyāyı̄ provide a unique¹⁷ view of how modern mathematics and computation rely on linguistic and cognitive skills. A thorough computational thinking underlying the Aṣṭādhyāyı̄ would perhaps allow a clear way to handle the linguist’s wish-list mentioned earlier—an effective understanding of cognitive skills, the use of induction, statistical prediction, data compression and formal concept analysis—in a succinct manner. For this purpose, more research is needed in Sanskrit itself as a language that has a complete detailed grammar. This in turn will possibly throw some light on how children acquire language, language learning in general, and ultimately lead to good language understanding systems along with the cognitive processes. Possibly, we may learn something like what is embedded in personal assistants like Siri, Google Assistant or Alexa¹⁸. In fact, with platforms like [14] being available, one could build systems for specialised families of sentences for experimental purposes for learning Sanskrit and use the effect of bootstrapping for enriching classes gradually. Such a study is quite likely to integrate machine learning, artificial intelligence as well as language formalism in a ubiquitous way. This will not only show the power of Pāṇini’s formalism but will also enable a clean adoption for other languages. The statement due to Kadvany [18] “Pāṇini is to spoken Sanskrit as Turing and other early logicians are to modern mathematics and early formalisms. Turing did not use a natural language like Sanskrit for his generative analysis” should provide some kind of holistic view.

Acknowledgements

First and foremost, humble salutations to the great muni, Pāṇini, who created the Pāṇinian grammar for Sanskrit for which there has rarely been a parallel in the linguistic history of civilisation. Further salutations go to Patañjali and Bhartṛhari whose contribution to the Pāṇinian system is immeasurable. Salutations also go to Bhartṛhari, whose treatise Vākyapadı̄ya is the single most important work in the long history of Pāṇinian grammar, and scholars worldwide generally refer to it as the Indian “philosophy of grammar”.

A large number of researchers from India and abroad have worked and contributed to the linguistic analysis of Sanskrit, adaptations of Pāṇinian grammar for a wider spectrum of natural-language analysis, as well as adapting Pāṇinian formalism for computational linguistics. In the context of Ingerman suggesting renaming of the famous BNF (Backus-Naur Form) as Pāṇini-Backus Form, Evelyn Lamb refers to this as “a feat of mathematical eponymy”, which is a testimony to convergence of areas like computer science and mathematics. While a large number of works are related to language/grammar analysis or applications to natural-language processing, authors of [5], [19], [17], [10], [11], [30], [32] have brought to light the underlying computational thinking aspects of the Aṣṭādhyāyı̄ from their own perspective, as well as the impact of the Pāṇinian system on various scientific developments. It is indeed a pleasure to thank these authors for bringing several subtle aspects from the perspective of computing. It is indeed a great pleasure to thank C.S. Aravinda and the Bhāvanā team who have significantly contributed to the editing of the article and, last but not least, my heartfelt thanks to C.S. Aravinda who convinced me on this journey.\blacksquare

References

1. A. Bharati, V. Chaitanya, K.V. Ramakrishnamacharyulu and R. Sangal, Natural language processing: a Pāṇinian perspective. New Delhi: Prentice-Hall of India; 1995.
2. A. Bharati, M. Bhatia, V. Chaitanya and R. Sangal. Pāṇinian grammar framework applied to English. South Asian Language Review, Creative Books, New Delhi, 1997.
3. L. Bloomfield, On Some Rules of Pāṇini, Journal of the American Oriental Society. 47 (1927) 61–70.
4. R. Briggs, Knowledge Representation in Sanskrit and Artificial Intelligence, The AI Magazine, Spring 1985, pp. 32-39.
5. G. Cardona, Pāṇini: A Survey of Research, Motilal Banarsidass Publishers, 1 January 1998 ISBN-10-8120814940.
6. G. Cardona, Pāṇini: His works and Its Traditions, Motilal Banarsidass Publishers, 1988.
7. G. Cardona, On the Structure of Pāṇini’s System, LNCS 5402, 2009, pp1-32, Springer-Verlag, ISBN 9783642001543.
8. A. Colmerauer, Les grammaires de metamorphose, Groupe d’Intelligence Artificielle, Universite de Marseille-Luminy (November 1975). Appeared as “Metamorphosis Grammars” in: L. Bole (Ed.), Natural Language Communication with Computers, (Springer, Berlin, May 1978).
9. V. Dahl, The Logic of Language, in The Logic Programming Paradigm: A 25-Year Perspective edited by K.R. Apt et al., Springer Berlin Heidelberg, pp. 429-456, Berlin, Heidelberg 1999.
10. A. Dash, Kāraka Theory For Knowledge Representation, web access: https://nagoya.repo.nii.ac.jp/.
11. A. Deliyanni and R.A. Kowalski, Logic and Semantic Networks, Communications of ACM, 22,3, March 1979, pp. 184-192.
12. P. Goyal, G. Huet, A. Kulkarni, P. Scharf and R. Bunker, A Distributed Platform for Sanskrit Processing, Proc. of COLING, pages 1011–1028, COLING 2012, Mumbai, India.
13. C.A.R. Hoare, Hints on Programming Language Design, Stanford Artificial Intelligence Laboratory memo aim-224, stan-cs-73-403, December 1973.
14. G. Huet, The Sanskrit Heritage Site, https://sanskrit.inria.fr/.
15. G. Huet and A. Kulkarni, Sanskrit Linguistics and Web Services, 25th COLING, 2014, Dublin, Ireland.
16. P.Z. Ingerman, Pāṇini Backus Form Suggested, Communications of ACM, Vol. 10, 3, 1967, pp. 137.
17. J. Kadvany, Pāṇinian Grammar and Modern Computation, History and Philosophy of Logic, 2015, http://dx.doi.org/10.1080/01445340.2015.1121439 .
18. J. Kadvany, Positional Value and Linguistic Recursion, J. Indian Philos. (2007) 35:487–520 DOI 10.1007/s10781-007-9025-5.
19. P. Kiparsky, Pāṇinian Linguistics, in R.E. Asher, ed., Encyclopaedia of Language and Linguistics, p. 2918-2923. Oxford, New York: Pergamon Press, 1994. Reprinted in R. Asher (ed.), Concise History of the Language Sciences. Pergamon Press, 1995.
20. P. Kiparsky, Pāṇini’s Razor, Symposium on Sanskrit and Computational Linguistics, Paris, Oct. 29-31, 2007.
21. E. Lamb, A Feat of Mathematical Eponymy, Scientific American Blog Network, https://blogs.scientificamerican.com/roots-of-unity/a-feat-of-mathematical-eponymy/
22. J.W. Lloyd, Foundations of Logic Programming, Springer-Verlag Berlin Heidelberg, 1984.
23. D. Maier and D.S. Warren. Computing with Logic, Logic Programming with Prolog. Benjamin/Cummings, Menlo Park/CA, 1988.
24. B. Meyer, Pictures Depicting Pictures, Proceedings of the 1992 IEEE Workshop on Visual Languages, Seattle/WA, September 1992.
25. A. Mishra, Simulating the Pāṇinian System of Sanskrit Grammar, First International Sanskrit Computational Linguistics Symposium, INRIA Paris-Rocquencourt, Oct 2007, Rocquencourt, France, INRIA-00207943
26. S. Nirenburg, Bar-Hillel and Machine Translation: Then and Now, 4th Bal Ilan Symp. on Artificial Intelligence, www.AAAI.org , 1995.
27. G. Penn, and P. Kiparsky, On Pāṇini and the Generative Capacity of Contextualized Replacement Systems, COLING 2012: 943-950
28. Fernando C.N. Pereira and David H.D. Warren, Definite Clause Grammars for Language Analysis—A Survey of the Formalism and a Comparison with Augmented Transition Networks, Artificial Intelligence 13 (1980), 231-278 North-Holland Publishing Company.
29. W. Petersen, A Mathematical Analysis of Pāṇini’s Śivasūtra, Journal of Logic, Language and Information 13: 471–489, 2004.
30. R.N. Sharma, The Aṣṭadhyāyı̄ of Pāṇini Vol. II English Translation of Adhyāya One with Sanskrit Text, Translation, Munshirm Manoharlal, 1 January 2002, ISBN-10-9788121510493
31. S.M. Shieber, An introduction to unification-based approaches to grammar. Brookline, Massachusetts: Microtome Publishing. Reissue of Shieber, Stuart M. 1986. An introduction to unification-based approaches to grammar. Stanford, California: CSLI Publications, http://nrs.harvard.edu/urn-3:HUL.InstRepos:11576719
32. F. Staal, Context-Sensitive Rules in Pāṇini, Foundations of Language, Jan 1965, Vol. 1, No. 1, pp. 63-72, Springer.
33. W.A. Woods, What is in a Link: Foundations for Semantic Networks, (BBN Report 3072, AI Report 38, Distributed by NTIS), in D. Bobrow and A. Collins, Eds., Academic Press, New York, 1975.

---

Appendix: A Brief Overview of Clausal Form of Logic

A clause is an expression of the form
\[ A_1,…, A_n \leftarrow B_1, …, B_m\] where A_1,…, A_n are called conclusions and B_1,…, B_m are called conditions. Both conclusions and conditions are of the form

\[P(t_1,…, t_r)\] called atom, where P is an r-ary predicate and t_1,…, t_r are called terms. Terms are constants, or variables or functional terms of the form
\[f(t_1,…, t_k)\] where f is a k-ary function and t_1,…, t_k are the terms.

A clause is said to be a definite clause, if the conclusion is at most one (i.e., n=1); in that case it is also a called a head in logic programming and the right side (the set of conditions) is called the body.

A clause is called a goal if there are no conclusions (n=0) and only conditions (m \geq 1).

If there are no conditions (m=0), then the clause is called a unit clause. Formal interpretation of a unit clause in logic programming is that “A is valid.”

The informal interpretation of definite clausal programs or logic programs are given below:

1. A program clause of the form A_1 \leftarrow B_1, …, B_m, is called a conditional rule that contains precisely one positive literal. A in the program clause is called the head and B_1,…,B_m is called body of the rule. The informal semantics of A_1 \leftarrow B_1,…, B_m in logic is that “for all interpretations, if B_1 \wedge … \wedge B_m is true, then A is true”. Formal semantics of the rule in logic programming is that “A is proved if B_1,… B_m are proved together” where A, B_1, B_2,…, B_n are predicates along with the arguments and the symbol \leftarrow denotes “implied by”.
2. A unit clause is a clause of the form A \leftarrow. This is an unconditional clause. Its informal semantics in logic is that “for all interpretations, A is true”.
3. A clause of the form \leftarrow B_1,…, B_n that has no positive literal (or no conclusion or consequent) is called a goal clause.
4. An empty clause is the clause with empty conclusion and empty condition. This clause is to be understood as a contradiction.
5. A logic program is a finite sequence of program clauses.
6. The meaning of a logic program P is the set of ground goals deducible from P; it uses SLD (Selective Linear Definite) clause resolution principle for deduction.

The reader is referred to [22] for further details.

Footnotes

1. In 2003, the UNESCO recognised the tradition of Vedic chanting as a masterpiece of the oral and intangible heritage of humanity (https://ich.unesco.org/en/RL/tradition-of-vedic-chanting-00062). ↩
2. Here is the precise description of these pāṭhas. If each word in the padapāṭha is enumerated according to the order in which it occurs, in its basic form in the saṁhitāpāṭha, as 1, 2, 3,…, the sentence formation in the kramapāṭha goes according to the pattern 1+2; 2+3; 3+4;… The pattern followed in the jaṭāpāṭha is: 1+2, 2+1, 1+2; 2+3, 3+2, 2+3,… and that followed in the ghanapāṭha is: 1+2, 2+1, 1+2+3, 3+2+1, 1+2+3,…. ↩
3. The names of the eight additional variations, called aṣṭa vikṛtis, can be easily recalled from the verse

   jaṭā mālā śikhā rekhā dhvajo daṇḍo ratho ghanah
   aṣṭau vikṛtayah proktāh kramapūrvā manı̄ṣibhih ↩

4. While this the widely prevalent form in which it is spelt and pronounced, the spelling Saṃskṛta is the norm in some of the Indian language cultures. Pāṇini uses the word Bhāṣā. ↩
5. Traditionally, children learnt to memorise the Amarakośa, a thesaurus that has families of words that are in use. ↩
6. The pre-Pāṇinian grammars are mostly unknown even though the Aṣṭādhyāyı̄ cites several earlier grammarians. The interested reader is referred to Cardona [5] who has made an exposition of these aspects in his book. ↩
7. Patañjali, one of the greatest scholars who lived around 200 BCE, composed a wide spectrum of works ranging from Yogasūtras to a treatise on the Aṣṭādhyāyı̄ of Pāṇini. His commentary (Bhāṣya) on the Aṣṭādhyāyı̄ is so revered in the Indian traditions that it is widely known simply as Mahābhāṣya”. ↩
8. Hence the name Aṣṭādhyāyı̄. ↩
9. The word terminal here literally means that it cannot be altered. The word non-terminal can be treated as a named place holder or simply a variable. ↩
10. Here is a brief explanation of these words. Ablative – Pañcamı̄-vibhakti; expresses motion away from something. Genitive – Ṣaṣṭhı̄-vibhakti; marks a noun to modify another noun. Nominative – Prathamā-vibhakti; subject of a verb. Locative – Saptamı̄-vibhakti; roughly corresponds to prepositions such as `at’ and `on’. ↩
11. A Hasse diagram of a partially ordered set is a drawing of the directed graph whose vertices are the elements of the set and whose edges correspond to the upper neighbour relation determined by the partial order. The drawing must meet the following condition: if an element x of the partially ordered set is an upper neighbour of an element y, then the vertex of x lies above the vertex of y. ↩
12. Biolinguistics was coined and defined at MIT in 1971, as a highly interdisciplinary subject as it related various fields such as biology, linguistics, psychology, anthropology, mathematics, and neurolinguistics to explain the formation of language, the reflection of which can be seen in the Pāṇinian grammar. ↩
13. A Latin phrase meaning, one of its kind, used to describe something considered unique. ↩
14. A brief overview of Horn Clause Programs is given in the appendix. ↩
15. Jeannette M. Wing coined this word to represent a universally applicable attitude and skill set that everyone, not just computer scientists, would be eager to learn and use. ↩
16. For discussions of Pāṇini’s system with respect to arithmetic, the reader is referred to [18]. ↩
17. A word of caution for the enthusiastic reader: It is quite hazardous to project contemporary mathematical ideas into its distant history. But, in the context of Pāṇini’s Aṣṭādhyāyı̄, a large evidence exists to relate the understanding of advanced formal methods to ancient Indian linguists. It must, however, be warned that some of the modern technology that is rooted in some of the mathematical abstractions should not be projected to history unless there is strong constructive evidence. ↩
18. Again, the reader is requested to remember the warning given earlier in the context of the formal methods underlying Pāṇini’s system. ↩