Mathematics in India

In the previous three parts of the series, we had presented glimpses of geometry and computational mathematics in Vedic and Sūtra Literature, especially the mathematics in the Śulba-sūtras and Piṅgalācārya’s Chandaḥ-sūtra; discussed the history and significance of the decimal system in India, emphasizing both the decimal nomenclature and the decimal place-value notation with zero; and described examples of explicit Indian algorithms for some fundamental arithmetic operations including algorithms for multiplication, long division and extraction of square roots.

In this part, we shall mention a few other topics from ancient Indian arithmetic.

Introduction

As mentioned earlier in ([7], p. 58), calculations in ancient India were usually performed on sand-dust (dhuli) spread on a board called pāṭī. In post-Vedic Indian treatises, the term pāṭīgaṇita is employed for the science of calculations (gaṇita) which requires the writing material pāṭī. Sometimes pāṭīgaṇita is simply called gaṇita. The carrying out of mathematical calculations was sometimes called dhuli-karma (dust-work). During the translation of Indian mathematics texts from Sanskrit to Arabic, the terms pāṭīgaṇita and dhuli-karma were rendered into their Arabic equivalents ilm-hisāb-al-takht (the science of calculations on the board) and hisāb-al-ghobār (calculation on dust) respectively.

What we now refer to as `arithmetic’ (as distinguished from abstract number theory) forms a major part of ancient Indian pāṭīgaṇita and in modern usage, pāṭīgaṇita is often taken to be a translation of `arithmetic’. However, in ancient Indian treatises, the subject pāṭīgaṇita (or gaṇita) includes, apart from computational arithmetic, geometry and mensuration, and some topics from what we now consider as a part of basic algebra. For instance, Brahmagupta (628 CE) and his commentator Pṛthudakasvāmī (c. 860 CE) include, in this subject, the rules of operations for the eight fundamental operations (addition, subtraction, multiplication, division, squaring, taking square roots, cubing, taking cube roots), rules for operations with fractions, the rule of three, the inverse rule of three, the rule of five, the rule of seven, the rule of nine, the rule of eleven, and rules for barter and exchange; and the computations of quantities arising out of problems on mixtures, progressions (or series), plane figures (geometry or mensuration), excavations, stocks (or piles of bricks), wood cutting, heaps or mounds (of grain) and shadows. Later texts also include a section on the arithmetic of zero. The Līlāvatī of Bhāskara II ([10], [12], [13]), a hugely popular treatise on pāṭīgaṇita written around 1150 CE, includes topics in algebra like solutions of quadratic equations, integer solutions of linear equations, combinations, permutations, and partitions.

Roughly speaking, all basic topics in mathematics which are needed in daily practical life, and which every student ought to learn, appear to have been accommodated under pāṭīgaṇita or gaṇita. Relatively advanced topics in algebra, which are presumably meant for more specialized scholars, are discussed separately—initially under the title kuṭṭaka and later under the title bījagaṇita, the now familiar Sanskrit term for algebra. The terms vyakta-gaṇita (science of calculations with the known) and avyakta-gaṇita (the science of calculations with unknowns) have also been used to distinguish between arithmetic (and other elementary topics) and algebra. The distinction between pāṭīgaṇita and bījagaṇita is not very rigid. For instance, there is some overlap in topics between the two texts Līlāvatī (on pāṭīgaṇita) and Bījagaṇita of Bhāskara II.

Among the topics in pāṭīgaṇita, the methods for performing the eight arithmetic operations listed above (addition, etc.) are considered the most fundamental by ancient Indian authors. A few weeks ago, in the television show `Kaun Banega Crorepati’ hosted by Amitabh Bachchan, a mathematics teacher named Gurudev, while arguing that mathematics was not at all a difficult subject, pointed out that unlike other subjects taught in school, everyone remembers the fundamental arithmetic operations taught at that primary stage, throughout their life. However, what was not mentioned in the programme, and is rarely highlighted anywhere, is that these methods, which are so easy to understand and remember, and which are of lifelong importance to all, are of Indian origin (as discussed in Part 3 of our article [7]). It is also not realized that while the methods are easy, the invention of these methods needed remarkable mathematical insight, sophistication and brilliance. We shall discuss our present attitude to these methods in the last section of the present instalment of this article.

We had already described examples of the Indian methods for performing some of the fundamental arithmetic operations in Part 3 of this series [7]. In the next section, we shall describe an Indian test method for checking the operations. The literature on arithmetic in Indian treatises is huge, some of which present a rich collection of interesting examples. In this article, we shall confine our discussions mainly to three representative topics: fractions, the rule of three, and progressions. For further principles and examples, we strongly suggest that the reader take a look at the books referred to at the end: the source-book by Datta-Singh [2] and the treatment of pāṭīgaṇita by Brahmagupta [8], Śrīdhara [15], Mahāvīra [11] and Bhāskara II ([10], [12], [13]). The Bakhshali Manuscript and treatises of Bhāskara I, Śrīpati and Nārāyaṇa Paṇḍita are also rich sources for principles and examples of arithmetic in ancient and medieval India.

Checks on the Fundamental Operations of Arithmetic

It is a common experience that, in spite of knowing the rules of arithmetic operations thoroughly, sometimes people do make mistakes during actual numerical calculations. This possibility of making a mistake induces nervousness during calculations, especially if the computations are to be made as a part of crucial scientific, commercial, administrative or other important financial work. It is therefore helpful to have methods which could possibly detect errors in calculations if any.

The treatise Mahāsiddhānta of Āryabhata II (c. 950 CE) describes such a method which was prevalent in India. The method has been described by the Persian scholar Ibn Sina (Avicenna) around 1020 CE and the Byzantine Greek scholar-monk Maximus Planudes (c. 1260–1305 CE); both of them attribute an Indian origin to the method.

For the reader’s convenience, we explain the method (described in the treatise Mahāsiddhānta in words) using modern notation.

To each number n associate a single-digit number f(n) as follows: add the digits of the number n to get s_1. If s_1 is a single digit, set f(n):=s_1; otherwise add the digits of s_1 to get s_2, then add the digits of s_2 to get s_3 and so on, till one arrives at some single digit s_{\ell}; then set f(n):=s_{\ell}.

For instance, consider n=287405. Then

s_1=2+8+7+4+0+5=26

and

s_2=2+6=8

so that

f(287405)=8.

Note that if the decimal expansion of n is

n=10^md_m+ \cdots + 100d_2+ 10d_1 + d_0,

where d_m, …, d_1, d_0 are the digits of n, then we have

s_1=d_m+ \cdots+ d_2+d_1+d_0

so that n-s_1 is divisible by 9, since 10^j-1 is divisible by 9 for every j. In the notation of congruences, we have n \equiv s_1 (mod 9).

Repeating the process, we have s_i \equiv s_{i-1} (mod 9) for every i so that finally we have n \equiv f(n) (mod 9).

The test rule in Mahāsiddhānta can be formulated as follows. Suppose c is the correctly computed product of k numbers n_1,n_2, …, n_k plus or minus another number r, i.e.,

c=n_1n_2 \cdots n_k \pm r.

Then f(c) would be:

f(c)=f(f(n_1)f(n_2) \cdots f(n_k) \pm f(r)).

In the previous part, we had demonstrated Brahmagupta’s zig-zag method for performing the multiplication 1223 \times 235 and had obtained the product 287405. Let us apply the above test to this.

We have

f(1223)=8

and

f(235)=f(10)=1

so that

f(f(1223)f(235))=f(8 \times 1)=f(8)=8

which matches

f(287405)=8

(computed above).

As the reader might have realized, the test rule in Mahāsiddhānta is an application of the principles of congruent arithmetic. One can see that, in case 9 divides n, f(n)=9; otherwise the number f(n) will be simply the remainder obtained by dividing the number n by 9. However, the method of repeated summing of digits is a much more convenient and fast way of computing f(n) than the usual long division method. The procedure is now known as the method of checking calculations by `casting out nines’. It bears a striking resemblance with modern computational error-detecting methods using similar modular arithmetic.

As with the methods of the fundamental operations, the rule of “casting out nines” is easy to implement even by a school-going child, but its invention required remarkable algebraic insights and skill, including a mastery of the basic principles underlying congruent arithmetic (without the notation).

Note that the method of “casting out nines” will not, by itself, detect the error if an erroneously obtained number differs from the correct number by a multiple of 9. Nārāyaṇa Paṇḍita (1356 CE) recommends testing operations by the casting out of any chosen number d (not necessarily 9), that is, by working with the remainders obtained by dividing the numbers involved by that chosen number d.

Fractions

The modern rules for the arithmetic of fractions are of Indian origin. We have become so used to them that we tend to overlook the facts that fractions had been a source of difficulty in other ancient civilizations, and that the modern (i.e., Indian) rules for operations with fractions contain ideas which were unfamiliar even to the Egyptians, who were generally proficient in arithmetic, and to the Greeks who had some of the most brilliant minds in the history of mathematics; and that these ideas came into general use in Europe only from the seventeenth century. For instance, ancient Egyptians handled only unit fractions (fractions with one in the numerator). Even as late as the 10th Century CE, Rabbi Saadia ben Joseph al-Fayyumi, a Hebrew writer in Egypt, made exclusive use of unit fractions resulting in laborious computations.

Etymology and Notation

In Indian arithmetic, the Sanskrit word bhinna, which means `broken’, has been used as the term for what we call `fraction’. This mathematical term bhinna was translated in Europe to corresponding terms like fractio, fraction, rotto which derive from Latin words for `broken’ like fractus (and frangere, `to break’) or ruptus.

In ancient Indian treatises, a fraction is represented as a pair of two integers written one above the other, just as we do now, but without the horizontal dividing line. For instance, the fraction \frac{848320}{14112} is written in the Bakhshali Manuscript as {848320}\atop{14112}.

The present practice of drawing a horizontal bar to separate the numerator and the denominator was introduced by the Moroccan mathematician Abu Bakr Al-Hassār in the late twelfth century and the Italian mathematician Fibonacci in the early thirteenth century.

Antiquity and Ubiquity of Fractions in India

References to fractions occur in India from the time of the Ṛg-Veda—the oldest extant literature. The Ṛg-Veda refers to the composite fraction \frac{3}{4} as tri-pada; the names of a few unit fractions occur in early Vedic literature.

The mensuration problems solved in the Śulba-sūtras, which are mentioned in Part 2 of this article (cf. [6] p. 52), show that Vedic Indians performed arithmetic operations (addition, subtraction, multiplication and even division) with composite fractions. However explicit statements of the rules for operations with fractions can be found only in post-Vedic treatises.

We mention one example to illustrate how familiar people had become with concepts on fractions by the early centuries of the Common Era. The process of reducing a fraction to its lowest terms (by removing the common factors between the numerator and the denominator), called apavartana, had become so well-known even among laymen that the revered Jaina scholar Umāsvāti (c. 150 CE) uses it in a non-mathematical work as a simile to illustrate a philosophical discussion ([2], p. 189):

Or, as when the expert mathematician, for the purpose of simplifying operations, removes common factors from the numerator and denominator of a fraction, there is no change in the value of the fraction, so …

Addition and Subtraction of Fractions

The rules for addition and subtraction of fractions

\frac{a}{b} \pm \frac{c}{d} = \frac{ad \pm bc}{bd}

involve the subtle idea of reducing fractions to a common denominator. For instance, \frac{a}{b} and \frac{c}{d} are replaced by their judiciously chosen equivalent expressions \frac{ad}{bd} and \frac{bc}{bd} respectively, so that both the new expressions have a common denominator.

The concept of reduction to a common denominator is seen highlighted prominently in some of the Indian mathematics treatises, and mentioned along with the above rules. For instance, Brahmagupta (628 CE) describes the reduction principle along with the laws of addition and subtraction as follows ([2], p. 189; [8], p. 5):

By the multiplication of the numerator and denominator of each of the (fractional) quantities by the other denominators, the quantities are reduced to a common denominator. In addition, the numerators are united. In subtraction, their difference is taken.

The rules for addition and subtraction appear in a terse form in the Āryabhaṭīya (499 CE) of Āryabhaṭa (cf. [16], p. 70) and are explained in detail by his commentator Bhāskara I (c. 600 CE).

Mahāvīra (850 CE) describes the LCM (Least Common Multiple) method, called niruddha, for reducing to a common denominator. This method for shortening computations with fractions occurs in Europe in the work of Nicolas Chuquet (1484 CE), and began to be generally recognized only as late as the seventeenth century.

Multiplication and Division of Fractions

The straightforward rule for multiplication \frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd} is explicitly mentioned by Brahmagupta and Bhāskara I. Mahāvīra refers to crosswise reduction or cancellation, whenever possible, to shorten the work. For instance, to multiply \frac{2}{3} with \frac{6}{4}, instead of multiplying the numerators and denominators, one could perform crosswise cancellation:

\frac{2}{3} \times \frac{6}{4} = \frac{2}{4} \times \frac{6}{3}= \frac{1}{2} \times \frac{2}{1}=\frac{2}{2}=1.

The idea of division by fractions by the method of multiplication of the inverted divisor, i.e., the rule

\frac{a}{b} \div \frac{c}{d}= \frac{a}{b} \times \frac{d}{c} =\frac{ad}{bc}

is mentioned clearly by Brahmagupta (628 CE). This rule occurs in subsequent Indian and Arab works, but appears in Europe only in the sixteenth century in the work of Michael Stifel (1544 CE), and becomes fairly common in Europe only in the seventeenth century.

Although Āryabhaṭa does not mention it separately as a rule on division by fractions, it occurs in his treatment of the Rule of Three for fractional quantities. His rule takes the form

\frac{\frac{a}{b} \times \frac{c}{d}}{\frac{m}{n}}=\frac{acn}{bdm}.

The standard rules for taking the square, square root, cube and cube root of a fraction are also mentioned explicitly by most post-Vedic authors of mathematics treatises.

Numerical examples are provided to make the reader adept in the use of the fundamental rules of operations with fractions. For instance, Śrīdhara asks the reader ([15], p. 20) to compute the sum of
\[\begin{align*}
3 \frac{1}{2} + \frac{1}{4} {\rm ~~ of ~~} 3 \frac{1}{2} + \frac{1}{6} {\rm ~~ of ~~}
\left(3 \frac{1}{2} + \frac{1}{4} {\rm ~~ of ~~} 3 \frac{1}{2}\right)
\quad {\rm with }\quad
\frac{1}{2} + \frac{1}{3} {\rm ~~ of ~~} \frac{1}{2} + \frac{1}{4} {\rm ~~ of ~~}
\left(\frac{1}{2} + \frac{1}{3} {\rm ~~ of ~~} \frac{1}{2}\right). \end{align*}\]

Some results of Mahāvīra on Unit Fractions

The above rules on fundamental operations with fractions are useful for practical applications. Mahāvīra also gives several interesting rules on unit fractions which appear to address sheer mathematical curiosities ([2], pp. 199–203). We quote a few of them. For convenience, we write down his verbal statements using algebraic notation.

By slightly modifying his formula for geometric progression, Mahāvīra expresses 1 as the sum of unit fractions

1= \frac{1}{2}+ \frac{1}{3}+ \frac{1}{3^2}+ \frac{1}{3^3}+ \cdots + \frac{1}{3^{n-2}} + \frac{1}{2 \times 3^{n-2}}.

Possibly applying the idea of telescopic sum, Mahāvīra writes down a unit fraction as the sum of fractions with specified numerators:
\[\begin{align*}
\frac{1}{n}&=\frac{a_1}{n(n+a_1)}+\frac{a_2}{(n+a_1)(n+a_1+a_2)} + \cdots
+\frac{a_r}{a_r(n+a_1+a_2+ \cdots +a_{r-1})}\end{align*}\]

Note that: \[\begin{align*}
\frac{a_1}{n(n+a_1)}&=\frac{1}{n}-\frac{1}{n+a_1},\\
\frac{a_2}{(n+a_1)(n+a_1+a_2)}&=\frac{1}{n+a_1}-\frac{1}{n+a_1+a_2},\quad \textrm{etc.}\end{align*}\]

Mahāvīra shows how to express a fraction \frac{p}{q} (with p,q coprime) as the sum of unit fractions as follows: choose i to be a number less than p such that q+i is a multiple of p and let r=\frac{q+i}{p}. Then

\frac{p}{q}=\frac{1}{r}+\frac{i}{rq}

and the process is repeated with \frac{i}{rq}. The process has to terminate as the numerators decrease at each step (for instance, i < p).

Ratio and Proportion: The Rule of Three

Ancient Indians effectively handled problems involving ratio and proportion using rules of simple proportion like the trairāśika (Rule of Three) and the vyasta-trairāśika (Inverse Rule of Three), as well as rules of compound proportion like pañcarāśika (Rule of Five), saptarāśika (Rule of Seven), navarāśika (Rule of Nine) and ekādaśarāśika (Rule of Eleven).

The Rule of Three and its Inverse

The Rule of Three occurs in the oldest extant post-Vedic treatises—the Bakhshali Manuscript (probably around 300 CE) and the Āryabhaṭīya (499 CE) of Āryabhaṭa—and all subsequent works. Problems involving the Rule of Three have the form:

If m yields f, what will r yield?

For instance, the following two problems have the above form:

1. If the price of m units of an object is Rs. f, then what is the price of r units of that object?
2. If a certain distance can be covered at a speed of m kmph in f hours, then how much time will be needed to cover the same distance at r kmph?

The three given quantities m,f,r are called respectively pramāṇa (measure), phala (fruit) and icchā (requisition). The required yield is called icchā-phala. Let us denote it by the algebraic notation x.

For clarity, we call m the standard quantity, f the standard result, r the desired quantity and x the desired result.

Case 1. The result increases (respectively, decreases) when the quantity increases (respectively, decreases), for instance, in Example (i) above.

In this case, the Rule of Three is stated verbally by Āryabhaṭa ([15], p. 68) as follows:

In the Rule of Three, multiply the phala by the icchā and divide the resulting product by the pramāṇa to obtain the icchā-phala.

Algebraically, one has to find x such that \frac{m}{f} = \frac{r}{x}. Thus, the desired result x is clearly \frac{f \times r}{m}. This is the algebraic interpretation of the Rule of Three, which is stated in words in the texts.

Case 2. The result decreases (respectively, increases) when the quantity increases (respectively, decreases), for instance, in Example (ii) above.

Let us discuss algebraically straightaway. In this case, one has f \times m =r \times x so that the desired result is x=\frac{f \times m}{r}. This is the Inverse Rule of Three.

Formulated algebraically, the Rule of Three appears obvious. However, while an algebraization of a problem makes things comfortable for the mathematically minded, it can make discussions incomprehensible for others who do not feel at home when articulated in the language of algebra. Many practical arithmetical problems require the Rule of Three or its variants. Therefore, the algebraic language is avoided while discussing arithmetical problems on the Rule of Three, as these would be relevant to large sections of the population.

We quote two examples of Śrīdhara ([15] p. 23; 25) illustrating the Rule of Three and Inverse Rule of Three respectively. Both involve fractions. Note: The weight of one paṇas equals the weight of four karṣas; the monetary amount of one purāṇa equals that of sixteen paṇas; one paṇa equals four kākiṇīs; one kākiṇī equals twenty varāṭakas.

Example 1. If one pala and one karṣa of sandalwood are obtained for ten and a half paṇas, for how much will be obtained nine pala and one karṣa?

More the money, more the sandalwood that can be obtained with it. Thus, taking m=1\frac{1}{4}=\frac{5}{4}, f=10\frac{1}{2}=\frac{21}{2} and r=9 \frac{1}{4}=\frac{37}{4}, the Rule of Three gives the price of nine pala and one karṣa to be:

\[\begin{align*} \frac{\frac{21}{2} \times \frac{37}{4}}{\frac{5}{4}} &=
\frac{21 \times 37 \times 4}{2 \times 5 \times 4}\\&= \frac{21 \times 37}{2 \times 5}\\&=\frac{777}{10}\\&=77+\frac{7}{10}\\&=
4 \times 16 + 13 +\frac{2}{4}+
\frac{16}{4 \times 20}\end{align*}\]
paṇas, i.e., 4 purāṇa, 13 paṇa, 2 kākiṇī and 16 varāṭaka.

Example 2. When a given quantity of pearls is measured at eight pearls a necklace, the number of necklaces is twenty. Tell, o mathematician, what would be the number of necklaces when the same quantity of pearls is measured at six pearls a necklace?

Here, if the number of pearls per necklace increases, then the total number of necklaces decreases. Thus, taking m=8, f=20 and r=6, the Inverse Rule of Three gives the number of necklaces as \frac{8 \times 20}{6}=\frac{160}{6}=26 \frac{2}{3}.

Note that the problem may also be solved by applying the Rule of Three twice.

First, one computes the total number of pearls. Taking m=1, f=8, r=20, one gets the total number, by the Rule of Three, to be \frac{8 \times 20}{1}=160.

Next, one asks the question: if six pearls are contained in one necklace, then how many necklaces will contain 160 pearls? Here, taking m=6, f=1, r=160, one gets the total number, by the Rule of Three, to be \frac{1 \times 160}{6}= \frac{160}{6}=26 \frac{2}{3}.

Appreciation of The Rule of Three

We see a high appreciation of the Rule of Three among Indians for its simplicity and its applicability to practical problems. In the context of this rule, Varāhamira (c. 505 CE) remarks ([2], p. 209):

If the sun performs one complete revolution in a year, how much does he accomplish in a given number of days? Does not even an ignorant person calculate the sun in such problems by simply scribbling with a piece of chalk?

To emphasize that the Rule of Three is the essence of arithmetic, Bhāskara II (1150 CE) gives the analogy ([2], p. 209):

As Lord Śrī Nārāyaṇa, who relieves the sufferings of birth and death, who is the sole primary cause of the creation of the universe, pervades this universe through His own manifestations as worlds, paradises, mountains, rivers, gods, men, demons, etc., so does the Rule of Three pervade the whole of the science of calculation. … Whatever is computed whether in algebra or in this (arithmetic) by means of multiplication and division may be comprehended by the sagacious learned as the Rule of Three.

He also asserts ([2], p. 210):

Leaving squaring, square-root, cubing and cube-root, whatever is calculated is certainly a variation of the Rule of Three, nothing else.

The Rule of Three, brought to Europe via the Arabs, was very highly regarded by merchants, during and after the Renaissance. It came to be known as the Golden Rule for its great popularity and utility in commercial computations. Much space used to be
devoted to this rule by early European writers on arithmetic. Robert Recorde¹ (1542 CE) refers to it as ([17], p. 484)

the Rule of Proportions, which for his excellency is called the Golden Rule.

The popular English arithmetician James Hodder of the seventeenth century writes ([17], p. 486):

as Gold transcends all other Metals, so doth this Rule all others in Arithmetick.

Compound Proportion

The Rule of Three is the fundamental rule of proportion. Rules of compound proportion like the Rule of Five, Rule of Seven, etc., are combinations of the Rule of Three. In such problems on compound proportion, there are two sets of terms: the first set in which all terms are present (i.e., known) is called pramāṇa pakṣa (measure side) and the second set in which one term is missing (i.e. unknown) is called the icchā pakṣa (requisition side).

Brahmagupta states a general rule known as the `Rule of Odd Terms’ from which all the above rules (Rule of Three, Rule of Five, etc.) follow as special cases ([2], pp. 211–212; [8], pp. 46–47):

In the case of odd terms beginning with three terms up to eleven, the result is obtained by transposing the fruits on both sides from one side to the other, and then dividing the product of the larger set of terms by the product of the smaller set. In all the fractions the transposition of denominators, in like manner, takes place on both sides.

We illustrate the general rule with the help of a numerical example (in three parts) on the Rule of Five from the Līlāvatī ([2], p. 213; [10], p. 83; [12], p. 145):

O mathematician! If the interest on a hundred be five per month, tell me what is the interest on sixteen for a year? Likewise, tell me the period given the principal and the interest, and what is the principal amount when the period and the interest are known.

The unit of currency is not specified in the verse. For convenience, let us take it to be niṣka (gold coin).

Case 1. To find Interest (given Principal and Time).

Here the pramāṇa pakṣa comprises:

Principal: 100 niṣka, Time: 1 month, Interest: 5 niṣka;

the icchā pakṣa comprises:

Principal: 16 niṣka, Time: 12 months, Interest: x niṣka.

The quantities may be arranged in a tabular form as

100	16
1	12
5	x

Here, the `fruits’ are in the third row and are to be interchanged to obtain:

100	16
1	12
x	5

(Note that, in our present mode of communication, the first two rows had to be copied again; but when ancient Indians did calculations on board (pāṭī), they had to simply erase the entries on the third row to interchange the entries and not do anything about the rest of the table.)

The larger set of known terms (i.e., three terms) is in the second column and the smaller set of known terms (i.e., two terms) is in the first column.

The product of the numbers in the former (i.e., the second column) is 16 \times 12 \times 5 =960, while the product of the known numbers in the latter (i.e., the first column) is 100 \times 1=100.

Therefore, the required result is \frac{960}{100}=\frac{48}{5}=9\frac{3}{5} niṣka.

Note: For convenience, henceforth, we will represent a fraction without the horizontal bar (as in ancient India) while writing it as an entry in a table; otherwise we will denote it with the bar as done in modern representation.

Case 2. To find the Time Period (given Principal and Interest).

Here the pramāṇa pakṣa comprises:

Principal: 100 niṣka, Time: 1 month, Interest: 5 niṣka;

the icchā pakṣa comprises:

Principal: 16 niṣka, Time: x months, Interest: \frac{48}{5} niṣka.

The quantities may be arranged in a tabular form as

100	16
1	x
5	48
	5

Transposing the `fruits’ (i.e., the numbers) in the third row, we obtain:

100	16
1	x
48	5
5

Transposing the denominators as stipulated, we obtain:

100	16
1	x
48	5
	5

Now, the larger set of known terms is in the first column and the smaller set in the second column.

The product of the numbers in the former is: 100 \times 1 \times 48 =4800 while the product of the known numbers in the latter is: 16 \times 5 \times 5=400.

Therefore, the required result is \frac{4800}{400}=12 months.

Case 3. To find the Principal (given Time Period and Interest).

Here the pramāṇa pakṣa comprises:

Principal: 100 niṣka, Time: 1 month, Interest: 5 niṣka;

the icchā pakṣa comprises:

Principal: x niṣka, Time: 12 months, Interest: \frac{48}{5} niṣka.

Now the initial tabular arrangement is:

100	x
1	12
5	48
	5

Transposing the `fruits’ (i.e., the numbers) in the third row, we obtain:

100	x
1	12
48	5
5

Transposing the denominators as stipulated, we obtain:

100	x
1	12
48	5
	5

Now, the larger set of known terms is in the first column and the smaller set is in the second column.

The product of the numbers in the former is 100 \times 1 \times 48 =4800, while the product of the known numbers in the latter is 12 \times 5 \times 5=300.

Therefore, the required result is \frac{4800}{300}=16 niṣka.

One can see the rationale of Brahmagupta’s rule here. For instance, in Case 1, one knows that the interest i is directly proportional to both the principal p and the time period t. If p_1, t_1, i_1 are the principal, time period and interest for the first set and p_2, t_2, i_2 are the principal, time period and interest for the second set with i_2 unknown, then \frac{p_1t_1}{p_2t_2}=\frac{i_1}{i_2}, so that, by the Rule of Three, i_2=\frac{p_2t_2i_1}{p_1t_1}, the special case of Brahmagupta’s Rule when applied here.

Before multiplying all the entries in the first column and all the entries in the second column and equating them, the `fruits’ i_1 and i_2 are transposed so that one obtains the relation p_1t_1i_2=p_2t_2i_1, i.e., \frac{p_1t_1}{i_1}=\frac{p_2t_2}{i_2}.

The rule regarding transpositions of the denominators (along with the rule about transposition of `fruits’) corresponds to the principle of division by fraction being the multiplication by its reciprocal.

Progressions or Series

Nowadays topics on finite series like the formulae for Arithmetic Progression (A.P.) or Geometric Progression (G.P.) are usually covered under Algebra. In ancient Indian treatises they are covered under Pāṭīgaṇita. The Sanskrit term for series is śreḍhī. We quote a few examples from the several formulae on finite series in these texts.

Āryabhaṭa (499 CE) describes the standard formulae for A.P. and related problems, including the general formulae for computing the sum of natural numbers, the sum of squares of natural numbers and the sum of cubes of natural numbers ([16], pp. 61–67).

Consider the A.P. series \{a_1, …, a_n\} with first term a_1=a, the common difference d (i.e., a_2=a+d, a_3=a+2d, etc.), the last term a_n=\ell, sum S and Arithmetic Mean M. Then Āryabhaṭa’s formulae give:

1. M=a+ \frac{(n-1)d}{2}.
2. S=n(a+ \frac{(n-1)d}{2}) = \frac{n(a+\ell)}{2}.
3. \ell= a+(n-1)d.<.li>
4. n=\frac{1}{2}[\frac{\sqrt{8dS+(2a-d)^2}-2a}{d}+1].

The formula (iv) is obtained as a solution to the quadratic equation

dx^2+(2a-d)x-2S=0

in the variable x formed from (ii) when S is known and x=n has to be determined.

More generally, for any number p, and the A.P. series with n terms beginning with the a_{p+1} defined above, i.e. the series

a+pd, a+(p+1)d, … , a+(p+n-1)d,

Āryabhaṭa states that the Arithmetic Mean M(p) and the sum S(p) are given by:

  v. M(p)=a+ (\frac{n-1}{2}+p)d.
  vi. S(p)=n(a+ (\frac{n-1}{2}+p)d).

Āryabhaṭa also states the formulae

  vii. 1+2+\cdots +n=\frac{n(n+1)}{2}.
  viii. 1^2+2^2+\cdots + n^2=\frac{n(n+1)(2n+1)}{6}.
  ix. 1^3+2^3+\cdots + n^3=(1+2+ \cdots +n)^2=\frac{n^2(n+1)^2}{4}.

Further, setting s_m:=1+2+\cdots +m, Āryabhaṭa gives the formula:

  x. s_1+s_2+\cdots +s_n=\frac{n(n+1)(n+2)}{6}=\frac{(n+1)^3-(n+1)}{6}.

The term citi is used in the sense of a series, while the term citighana is used for the above series s_1+s_2+\cdots +s_n. The term citighana literally means `the solid contents of a pile (say, of balls) in the shape of a pyramid on a triangular base’. The pyramid is so constructed that there is s_1=1 ball at the top, s_2=1+2 balls at the next lower layer, s_3=1+2+3 balls in the third layer from the top, and so on; at the base is the nth layer comprising s_n=1+2+ \cdots +n balls. Thus, the citighana s_1+s_2+\cdots +s_n is the number of balls in the solid pyramid.

Likewise, the series 1^2+2^2+\cdots + n^2 is termed vargacitighana, which literally means `the solid contents of a pile (of balls) in the shape of a pyramid on a square base’. Here, there is 1^2=1 ball in the topmost layer, 2^2 in the next lower layer, and so on; at the base, there are n^2 balls.

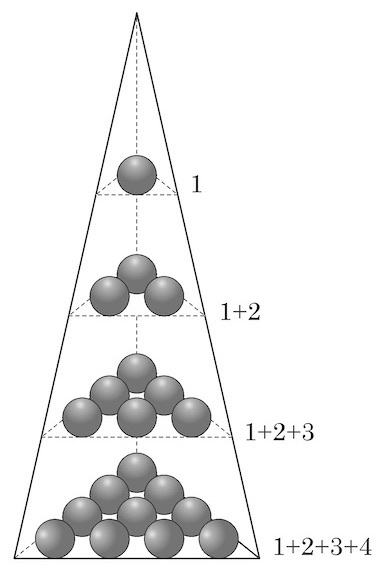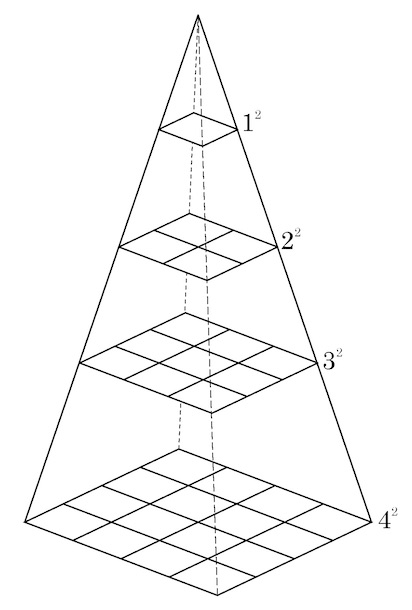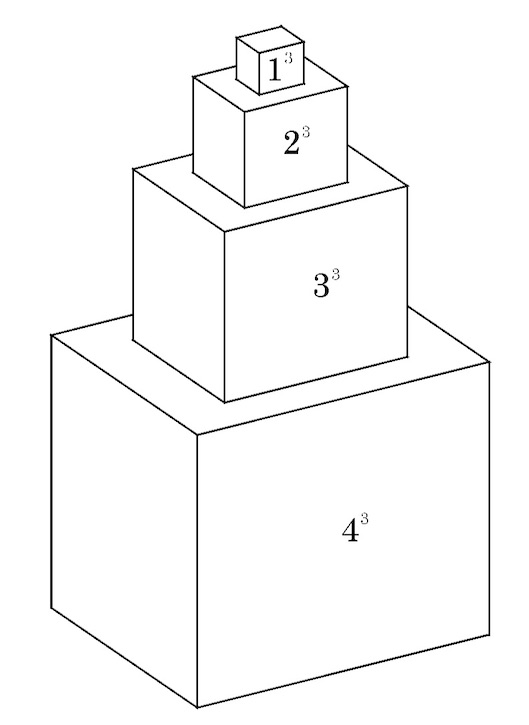The series 1^3+2^3+\cdots + n^3 is termed ghanacitighana, `the solid contents of a pile (of cuboidal bricks) in the shape of a pyramid having cuboidal layers’. Here, there is 1^3=1 brick in the topmost layer, 2^3 in the next lower layer, and so on; at the base, there are n^3 bricks.

The arithmetico-geometric topic citi (piles of shots) is given prominence in Indian treatises or chapters on pāṭīgaṇita—they contain a separate section citi on the theme. This also explains why it has been imperative for Indian mathematicians to include the algebraic formulae on progressions under pāṭīgaṇita.

Śrīdhara (750 CE) gives ([15], pp. 83–85) a formula for the sums of the series in (viii), (ix) and (x), and generalizations of the summation formulae (viii) and (ix):

  xi. \sum_{r=1}^n s_r + \sum_{r=1}^n r^2 + \sum_{r=1}^n r^3= \frac{n(n+1)^2(n+2)}{4}.

  xii. a^2 +(a+d)^2+ (a+2d)^2+ \cdots + (a+ (n-1)d)^2
    = [a+(a+2d)+(a+4d)+\cdots \mathrm{~to~} n \mathrm{ ~terms~}]\times a
   +[1^2+2^2+3^2+ \cdots+ (n-1)^2]\times d^2.

  xiii. a^3 +(a+d)^3+ (a+2d)^3+ \cdots + (a+ (n-1)d)^3= S^2 \times d + a \times S \times (a-d).

Note that in (xii), the summation formulae for the two terms on the right-hand side are already known.

Śrīdhara (750 CE) and Mahāvīra (850 CE) give the formula for G.P.:

  xiv. a+ar+ \cdots + ar^{n-1}=\frac{a(r^n-1)}{r-1}; ~~ r >1.

As we have seen in the second part of this article ([6], p. 55), the special case of the formula for a=1, r=2 is implicit in sūtra-s 8.32-8.33 of Chandaḥ-sūtra by Piṅgalācārya (c. 300 BCE).

Nīlakaṇṭha (1500 CE) gives the formula for infinite G.P.:

  xv. a + ar + ar^2 + ar^3 + \cdots = \frac{a}{1-r}; ~ |r| <1.

The special case of the infinite series, for a=1, r=\frac{1}{4}, has been used earlier by Vīrasena (c. 816 CE) for computing the volume of the frustum of a right circular cone ([14], pp. 203–05).

Miscellaneous Topics

Accountancy and Commercial Arithmetic in Ancient India

The development of arithmetic in ancient India appears to have been strongly influenced by mathematical problems arising out of commerce and accounting. Indeed, the ancient Indian treatises on arithmetic (rather pāṭīgaṇita or gaṇita) abound in commercial and related problems like income and expenditure, profit and loss, barter and exchange, simple and compound interest, discount, partnership, computations of the average impurities of gold and other problems on alligation (calculation of values or properties of a mixture), speeds and distances, and cistern problems. Many of the problems make use of The Rule of Three and its extensions, glimpses of which we have seen in this article. A few problems make use of the solutions of quadratic equations—we give an example below. We will also briefly recall the concept of the weighted arithmetic mean which is involved in some of the excavation and alligation problems.

The strong accountancy culture has been nicely summarised by David Mumford ([9] p. 122) in the following words:

In India, very sophisticated principles of accounting were codified in Kauṭilya’s comprehensive manual of statecraft, the Arthaśāstra written in the 4th century BCE. The Arthaśāstra covers in amazing detail every aspect of setting up and the managing of a kingdom (including managing a special forest for elephants). In Book II, Chapter 6 and also in many later chapters of Book II, Kauṭilya details how accounts are to be kept. He describes a complete system of book-keeping: he has a ledger for income with dates, times, payers, categories, etc., and a ledger for expenditures and finally a third ledger for balances. There are sections on auditing, insurance against theft, debtors, borrowings, mortgages, etc., and subtler accounting issues such as current vs. deferred receipts, how to account for price change of items in inventory, fixed vs. variable costs. Although he does not use negative numbers explicitly, he is clearly aware of how accounts must sometimes show a deficit and that people may carry a negative net worth.

It is speculated that this strong tradition of accounting led naturally to the concept of negative numbers in Indian mathematics at a very early date, which will be discussed in the next part of this article.

In the context of the Arthaśāstra, one is reminded that on the very first page of the Editorial of the inaugural issue of the journal Sankhyā (1933), P.C. Mahalanobis emphasizes that

administrative statistics had reached a high state of organization before 300 B.C.

Mahalanobis points out² that the Arthaśāstra of Kauṭilya

contains a detailed description for the conduct of agricultural, population, and economic censuses in villages as well as in cities and towns on a scale which is rare in any country even at the present time.³ … The detailed description of contemporary industrial and commercial practice points to a highly developed statistical system.

The Arthaśāstra also emphasizes independent cross-verification of the collected data.⁴

Weighted Arithmetic Mean in Ancient India

The weighted arithmetic mean of n quantities x_1, x_2, …, x_n with respective weights w_1, w_2, …, w_n is defined to be \frac{w_1x_1+\cdots+w_nx_n}{w_1+\cdots+w_n}. In a previous article in Bhāvanā ([4]), we had seen that this concept has been defined and applied in ancient Indian texts both as an exact mathematical formula and as a statistical representative or estimate. The terms used for the arithmetic mean include samarajju and samamiti.

The weighted arithmetic mean is used as a mathematical formula to combine different investments (with simple interest) into an equivalent single investment, and to compute the proportion of pure gold in an alloy formed by blending several pieces of gold of different weights and purities. Several examples have been given in Section 4 of the Bhāvanā article [4] (pp. 31–34).

The weighted arithmetic mean is also used to specify the (average) depth, width or length of an irregular-shaped pool of water and thereby estimate its volume. In this sense of a statistical estimate, a representative value, the weighted arithmetic mean occurs at least from the time of Brahmagupta (628 CE). Historians of statistics do not find this concept in European treatises prior to the late sixteenth or seventeenth centuries. Detailed discussions have been made in the Bhāvanā article ([4]).

We end this section by quoting two problems in arithmetic of different flavours from ancient Indian texts.

Interest Problem involving a Quadratic Equation

Brahmagupta (628 CE) addresses the following problem ([8], p. 62): Suppose the principal P is lent out at a certain rate of interest for T_1 months. At the end of the period, the (unknown) interest x that has accrued is again lent out at the same rate of interest for T_2 months. If the interest accrues to a known amount A, find the unknown interest.

If r is the rate of interest, then the conditions give the relations x=PrT_1 and A=x+xrT_2. Eliminating r, we get the quadratic equation

T_2x^2+PT_1x -PT_1A=0,

which yields the interest
\[\begin{align*}
x&=\frac{\sqrt{(PT_1)^2+4T_1T_2PA} – PT_1}{2T_2}\\
& =\sqrt{\frac{APT_1}{T_2}+(\frac{PT_1}{2T_2})^2} – \frac{PT_1}{2T_2},
\end{align*}\]

as mentioned by Brahmagupta in words (we add symbols in bracket for the convenience of the reader who can readily see the correspondence between the verbal description with our above notation):

Multiply the principal (P) by its time (T_1) and divide by the other time (T_2), and place the result (\frac{PT_1}{T_2}) at two places. Multiply the first of these by the mixture (A). Add to this the square of half the other. Take the square root of this sum. From the result subtract half the other. This will be the interest (x) on the principal.

Note that, for our convenience, we have discussed the problem using algebraic notation. We clearly see that the problem has been solved by the formation of a quadratic equation. However, the discussion in Brahmagupta’s chapter on Gaṇita avoids the use of algebraic terminology for wider accessibility—the solution is given as a verbal instruction which can be implemented even by a layman who is not mathematically minded.

The problem and its solution are stated earlier (in words) by Āryabhaṭa for the case T_1=1.

Meeting of Two Travellers: Relative Speeds, Distance and Time

Suppose a traveller is advancing daily at a certain speed and has already covered a certain distance. How much time will it take for a messenger, who starts later but at a faster speed, to catch up with the traveller? This famous `Problem of Messengers’, involving relative motion of two objects, originates in Āryabhaṭīya of Āryabhaṭa (499 CE).

Suppose v_1 and v_2 are the speeds of two moving bodies with v_2 > v_1 and d the distance between them. Āryabhaṭa’s rules can be formulated as follows:

1. If the two bodies are moving in opposite directions towards each other, then the time T that will elapse before they meet is given by T=\frac{d}{v_1+ v_2}.
2. If the two bodies have already met and are moving away from each other, then the time T that has elapsed after they met is given by T=\frac{d}{v_1+ v_2}.
3. If the two bodies are moving in the same direction with the faster body behind, then the time T that will elapse before they meet is given by T=\frac{d}{v_1 - v_2}.
4. If the two bodies have already met and thus the slower body is behind, then the time T that has elapsed after they met is given by T=\frac{d}{v_1 - v_2}.

Appreciation of Arithmetic in Ancient India

We have seen in the first part of the series ([5], p. 26), that mathematics is held in high esteem in Vedic, Vedāṅga, Jaina and Buddhist literature. There are again elaborate assertions on the importance of different branches of mathematics in post-Vedic mathematics treatises. As an example, we quote a long passage on the importance of Gaṇita from the text Gaṇita-sāra-saṅgraha (850 CE) of Mahāvīra ([2], pp. 5-6):

In all transactions which relate to worldly, Vedic or other similar religious affairs, calculation is of use. In the science of love, in the science of wealth, in music and in drama, in the art of cooking, in medicine, in architecture, in prosody, in poetics and poetry, in logic and grammar and such other things, and in relation to all that constitutes the peculiar value of the arts, the science of calculation is held in high esteem. In relation to the movements of the sun and other heavenly bodies, in connection with eclipses and conjunctions of the planets, and in connection with the direction, position, time and the course of the moon—indeed in all these, it is utilized. The number, the diameter and the perimeter of islands, oceans and mountains; the extensive dimensions of the rows of habitations and halls belonging to the inhabitants of the world, of the interspace between the worlds, of the world of light, of the world of the gods and of the dwellers in hell, and other miscellaneous measurements of all sorts—all these are made out by the help of gaṇita. The configuration of living beings therein, the length of their lives, their eight attributes, and other similar things; their progress and other such things, their staying together, etc.—all these are dependent upon gaṇita. What is the good of saying much? Whatever there is in all the three worlds, which are possessed of moving and non-moving beings, cannot exist as apart from gaṇita.

With the help of the accomplished holy sages, who are worthy to be worshipped by the lords of the world, and of their disciples and disciples’ disciples, who constitute the well-known series of preceptors, I glean from the great ocean of the knowledge of numbers a little of their essence, in the manner in which gems are picked from the sea, gold from the stony rock and pearl from the oyster shell; and give out according to the power of my intelligence, the Sāra-saṅgraha, a small work on gaṇita, which is however not small in value.

One can feel the passion with which the author communicates the indispensability of gaṇita for any person in any sphere of activity.

Our Present Attitudes towards Computational Mathematics

In ancient Greece, a sharp distinction was made between

1. `Arithmetic’, what is now called `Number Theory’, the study of the abstract properties of numbers; and
2. `Logistic’, what is now called `Arithmetic’ in school mathematics, the art of practical computations.

The indispensability of `logistic’ or computational mathematics for businessmen and men of war was of course recognized during all periods of Greek history. But, usually, `logistic’ was considered appropriate only for such practical purposes and not for serious mathematics. Euclid’s Elements has profound results on geometry and the abstract properties of numbers, but no place for `logistic’ or computational mathematics.

For instance, in Euclid’s Elements, we find the implicit occurrence of the result often referred to by the misnomer `Division Algorithm’ (quoted as the Remainder Principle in the previous two parts of the present article: [6], p. 44 and \cite {Du3}, p. 59). But this result is only a theoretical existential statement about the quotient and the remainder of a division. One does not see in ancient Greek treatises any effort to find an efficient method for computing quotient and remainder analogous to the ancient Indian long division method described in the previous part of this article ([7], pp. 59–60). We clarify here that Archimedes was an exception to this general condescending attitude among Greek mathematicians towards the science of computations.

As we have seen, in India, the science of calculations, gaṇita, has been held in high esteem in both Vedic as well as post-Vedic periods.

However, our present attitude to mathematics (even in India) is largely shaped by the typical Greek view of mathematics. In particular, consciously or subconsciously, a low status is accorded to the science of computations—the `logistic’ of ancient Greeks or the `arithmetic’ of modern school mathematics—as compared to the branches of mathematics named `Geometry’, `Algebra’, or `Calculus’.

Besides, there is the paradox that once invented, the implementation of an outstanding and neat computational method usually becomes a routine activity not requiring `brilliant’ mathematical ability unlike, say, the application of theorems to solve difficult `riders’ in geometry. This again brings down the status of computational mathematics among mathematics enthusiasts.

But as highlighted in the previous parts of this article, the methods of Indian arithmetic are really algebraic in character and their invention needed brilliant algebraic insights. Thanks to their efficiency, these methods can be learnt easily by children and, ironically, it is due to the very efficiency and consequent simplicity of these methods, that the admiration their inventions deserve is not accorded to them. At present, there is rarely a proper analysis of the ideas involved in these algorithmic methods (as distinct from mere mechanical learning and implementation) even among mathematically motivated students.

We shall now discuss the detrimental effects of the contemptuous attitude towards computational mathematics.

Foremost, we lose the excellent pedagogic scope that basic arithmetic provides in promoting critical appreciation, creativity, and the art of discovery in mathematics among school students from an early age. Once students learn the rudiments of algebra, at least the mathematically bright students could be encouraged to figure out why the methods of school arithmetic work, and to ponder how the algebraic principles were seized upon to invent such algorithms.

This brings us to the pedagogic potential of the history of mathematical ideas. In his plenary lecture at the International Congress of Mathematicians (ICM) 1978, André Weil quotes the following statement of Wilhelm Leibniz on the history of mathematics (both the original and the following translated version occur in [18], p. 227):

Its use is not just that History may give everyone his due and that others may look forward to similar praise, but also that the art of discovery be promoted and its methods known through illustrious examples.

Weil adds ([18], p. 229):

Deviating only slightly from Leibniz, we may say that its first use for us is to put or to keep before our eyes “illustrious examples” of first-rate mathematical work.

Indeed, well-chosen episodes from the history of ancient Indian mathematics can be used, even at the school level, to illustrate how mathematical ideas develop. For instance, Brahmagupta’s zigzag method for multiplication, described in the previous part of the article ([7], p. 59), can be used to demonstrate how the decimal system and algebraic ideas were used to invent an outstanding method for multiplication which works marvellously in the sand-board medium (or our present chalk and slate system), and how they are appropriately modified for the later paper-and-ink medium of writing.

Likewise, as discussed in ([7], pp. 61–62), one can use Āryabhaṭa’s algorithm (499 CE) for extraction of the square root to demonstrate how the ideas in the decimal system, especially the place-value and the zero, the method of long division, and the formula (a+b)^2=a^2+2ab+b^2 were seized upon by a mathematician in a remote past to invent such a method. These underlying principles are more transparent in the original method. Then one can see how a few steps of the algorithm are contracted to arrive at the current method.

But how many otherwise inquisitive students ever wonder why, say, the algorithm for square root works? Or, are encouraged by teachers (even the motivated ones) to think about it? Is the indifference due to a deep-rooted snobbish prejudice, a legacy perhaps of the Greeks, that these arithmetical methods are “algorithms” or “calculations” and not “mathematics”? Indeed, too often one comes across the undermining of computational innovations as being `mere calculation tricks’. But then, by such attitudes, are we not depriving students of early training in the art of mathematical discovery?

In high school, students learn the formula ^{n}C_r = \frac{n(n-1)(n-2) \cdots (n-r+1)}{1\cdot 2\cdot 3 \cdots r}; they also see the result ^{n+1}C_r = {}^{n}C_r + ^{n}C_{r-1} as an identity among binomial coefficients. Will it not strengthen them as mathematics thinkers, if they see how, more than two millennia ago, the ancients had not only observed the algebraic identity but seized upon it to recursively determine the values of ^{n}C_r through simple additions, completely bypassing the computationally complex operations of multiplication and division (cf. [6], pp. 58–59)?

In future parts of this article, we shall see that ancient Indian algorithms for finding integer solutions of equations are a potential source of profound ideas and techniques for enriching the more advanced students of mathematics. Āryabhaṭa’s kuṭṭaka algorithm prepares the mind for the `divide and conquer’ strategy in computational mathematics (cf. [6], pp. 54-55) as well as the principle of descent in abstract mathematics. Brahmagupta’s bhāvanā is a major step in an algorithm as well as a sophisticated abstraction, while the bhāvanā and the cakravāla are magnificent examples of marvellous interplays between abstract and algorithmic mathematics (partly discussed in [3]; may be further elaborated in the future).

The perpetuation of the prejudice among mathematics students against the science of computations may be all the more injurious now for future researchers, especially in algebraic mathematics. During a major part of the twentieth century, when mathematicians could revel exclusively in elegant existential arguments, the attitude of avoiding computational research might not have been that serious. But, as the constructive approach is gaining increasing importance in mathematics research, it is imperative to develop a taste for sophisticated computational mathematics.

It will therefore be all the more unfortunate if people involved in mathematics education continue to undermine the algorithmic and computational aspects of the subject. It is to be hoped that this negative attitude will be replaced by an enlightened positive attitude and that mathematically motivated young students will be encouraged to develop their aptitude and talent for the computational and algorithmic aspects of the subject too.

Apart from the pedagogic issues, our appreciation of ancient Indian mathematics becomes skewed and incomplete if we fail to recognize the mathematical sophistication involved in its methods for fundamental operations and other algorithms. Fortunately, the decimal system is hailed as a great invention, in spite of its simplicity, thanks to numerous perceptive comments from various celebrated thinkers. But how many times, in recent decades, do we see the algorithms for multiplication and other arithmetic operations being listed among the great Indian inventions in mathematics? Perhaps the highlighting of the algebraic character of the methods may help people realize their true mathematical merit.

Early thinkers on the development of mathematics had showered high praise for the arithmetic developed by Indians, based on the decimal system. We cite two examples. More than two hundred years ago, the great French mathematician Pierre-Simon Laplace had referred to modern arithmetic, based on the decimal system, as being “in the first rank of useful inventions” ([7], p. 5).

In the very first paragraph of the first page of the first chapter (Introduction) of his classic treatise A History of Mathematics, the American historian of mathematics F.~Cajori remarks ([1], p.1):

The chemist smiles at the childish efforts of alchemists, but the mathematician
finds the geometry of the Greeks and the arithmetic of the Hindus as useful and admirable as any research of today.

References

• [1] F. Cajori: History of Mathematics, Macmillan (1919), AMS Chelsea (2000).
• [2] B. Datta and A.N. Singh, History of Hindu Mathematics Part I, Motilal Banarsidass (1935); reprinted by Asia Publishing House (1962) \& Bharatiya Kala Prakashan (2004).
• [3] A.K. Dutta, The bhāvanā in Mathematics, Bhāvanā 1(1), 13–19 (2017).
• [4] A.K. Dutta, Weighted Arithmetic Mean in Ancient India, Bhāvanā 1(4), 24–36 (2017).
• [5] A.K. Dutta, Mathematics in Ancient India Part 1: Geometry in Vedic and Sūtra Literature, Bhāvanā, 6(1), 23-33, (2022).
• [6] A.K. Dutta, Mathematics in Ancient India Part 2: Computational Mathematics in Vedic and Sūtra Literature, Bhāvanā, 6(2), 43-61, (2022).
• [7] A.K. Dutta, Mathematics in Ancient India Part 3: The Decimal Notation and some Arithmetic Algorithms Bhāvanā, 6(3), 50-67, (2022).
• [8] V.D. Heroor (tr.), Brahmaguptagaṇitam, Chinmaya International Foundation Shodha Sansthan, Ernakulam (2014).
• [9] D. Mumford, What’s so Baffling About Negative Numbers? Studies in the History of Indian Mathematics (ed. C.S. Seshadri), Hindustan Book Agency, 113–143 (2010).
• [10] K.S. Patwardhan, S.A. Naimpally, S.L. Singh (eds.), Līlāvatī of Bhāskarācārya. Motilal Banarsidass (2001).
• [11] M. Raṅgācārya (ed. with English translation and notes), The Gaṇita-sāra-saṅgraha of Mahāvīrācārya, Govt. of Madras, Madras (1912).
• [12] A. Padmanabha Rao, Bhāskarācārya’s Līlāvatī Part I, Chinmaya International Foundation Shodha Sansthan, Ernakulam (2015).
• [13] A. Padmanabha Rao, Bhāskarācārya’s Līlāvatī Part II, Chinmaya International Foundation Shodha Sansthan, Ernakulam (2014).
• [14] T.A. Sarasvati Amma, Geometry in Ancient and Medieval India, Motilal Banarsidass, Delhi (1979; revised 1999).
• [15] K.S. Shukla (ed.), The Patiganita of Sridharacarya, Lucknow University (1959).
• [16] K.S. Shukla and K.V. Sarma (eds.), Āryabhaṭīya of Āryabhaṭa. Indian National Science Academy (1976).
• [17] D.E. Smith, History of Mathematics Vol II, originally 1925; Dover (1958).
• [18] André Weil, History of Mathematics: Why and How, Proceedings of the International Congress of Mathematicians, Helsinki 1978 Vol 1 (ed. O. Lehto), Helsinki, 227–236 (1980).

Footnotes

1. Robert Recorde (1510–58 CE) was an influential English writer on mathematics who is credited with introducing algebra in England. He introduced the `equals’ sign (=) in 1557. ↩
2. P.C. Mahalanobis, “Why Statistics?”, Sankhyā, Vol. 10(3), 196-197, 1950. ↩
3. Italics are ours, for emphasis. ↩
4. See P.C. Mahalanobis, op.cit., for the actual passages. ↩