Metre matters: The Āryā as expounded by Piṅgalācārya

Most of the mathematical and astronomical works in ancient India were written in the form of poetry. Unsurprisingly, translations of, and commentaries on, these works concentrate on the technical content of the verses and ignore their poetic aspects. This article primarily aims to present a systematic introduction to the āryā metre and its variations based on the Chandaśśāstra, the foundational text on prosody by Piṅgalācārya. It also presents a few examples from the monumental work of Āryabhaṭa, namely, the Āryabhaṭīya with the intention of creating a basic awareness and appreciation of this unique feature of Indian astronomy and mathematics: the combination of poetry with technical content, and its advantages in preservation of content as well as error detection.

Introduction

India has had a long tradition of passing down knowledge through oral transmission from guru to śiṣya and from generation to generation. This oral transmission was facilitated by presenting the knowledge in the form of verses which were rhythmical in nature making them easy to chant and therefore, memorize. The oral tradition did not remain confined to disciplines such as art, music and dance, but got extended to technical fields like astronomy and mathematics as well, and continued even after the advent of written works. A glimpse of the poetic beauty in the works of Indian astronomers and mathematicians has been recently brought to light by some scholars [2], [5].

Works by Āryabhaṭa (Āryabhaṭīya, 5th Century CE), Bhāskara I (Laghu-bhāskarīya, Mahā-bhāskarīya and others, 7th Century CE), Bhāskara II (Līlāvatī and others, 12th Century CE), Nārāyaṇa Paṇḍita (Gaṇita-kaumudī, 14th Century CE), Nīlakaṇṭha Somayājī (Tantrasaṇgraha, 16th Century CE), to name just a few, are evidence of this tradition. In fact, the tradition of composing mathematical works in poetic form dates back at least to the period of Vedāṅga-jyotiṣa (c. 1400 BCE) and has continued till the later part of the 19th century CE when Samanta Chandrasekhara¹ wrote an extensive astronomical treatise, Siddhānta-darpaṇa.

In this article, we first discuss some basic terms needed to understand the various metres employed in Sanskrit prosody. We then study in detail the characteristics of the āryā metre in particular. The choice to discuss the āryā metre is based on the fact that some of the earliest and fundamental treatises such as the Āryabhaṭīya, the Brahma-sphuṭa-siddhānta, etc., are composed entirely in this metre. Then we move on to examine some verses from the Āryabhaṭīya and see how they employ the āryā metre and its variations. We also discuss how this style of writing in poetic metres has an inbuilt error-detection mechanism which helps guard against mistakes creeping in while copying the texts, and correcting them even at a later date.

Basic Terminology

Before engaging in a study of metres, it would be useful to get introduced to some basic terms employed in Sanskrit grammar as well as prosody in order to fully appreciate the discussion.

Akṣara

Alphabets in Sanskrit are called varṇas and are divided into two sets: vowels and consonants. A suitable combination of these two form a word (pada). For example, consider a pada in the form of the proper name आ र्य भ ट (Āryabhaṭa). It has four components:

1. आ (ā) which is a standalone vowel
2. र्य (rya) which is composed of two consonants and a vowel: र् (r) + य् (y) + अ ( a)
3. भ (bha) which is composed of one consonant and a vowel: भ् (bh) + अ (a)
4. ट(ṭa) which is again composed of one consonant and a vowel: ट् (ṭ) + अ (a)

Each of these components form an akṣara. From these examples, we can say that an akṣara has exactly one vowel which may or may not be preceded by one or more consonants. Additionally, there could sometimes be an anusvāra ( ं) or visarga ( ः) that follows the vowel in an akṣara. For example, consider the following sentence:

Here, the akṣaras taṃ and ndaḥ may be further split into:

Thus, these akṣaras end with the anusvara ṃ and the visarga ḥ following the vowel a, respectively.

A word could also end in a non-vowel sound. In this case, the last sound is considered as part of the last akṣara. For example, the sentence given above ends in स्त्रम् (stram) = स् (s) + त् (t) + र् (r) + अ (a) + म् (m). This is considered as a single akṣara even though it ends in the sound म् (m) and not in a vowel. Note that this akṣara, in spite of having four consonants, still contains only one vowel.

Laghu and guru akṣara

Depending on the time taken to render them, the vowels are further classified as short or long.

Short vowels: अ (a), इ (i), उ (u), ऋ (ṛ), ऌ (ḷ)

Long vowels: आ (ā), ई (ī), ऊ (ū), ॠ (ṝ), ए (e), ऐ (ai), ओ (o), औ (au)

Like vowels, akṣaras are divided into two categories: laghu and guru. However, this is not decided only by the vowel associated with the akṣara. In his commentary on Piṅgala’s Chandaśśāstra, called the Mṛtasañjīvanī, Halāyudha explains the conditions for an akṣara to be a laghu or guru with a few sūtras [1, 1.9–1.13]. In what follows, we present these sūtras along with brief translations and explanations.

The implication of this sūtra is that a short vowel like ऋ (ṛ) makes the associated akṣara गृ (gṛ) a laghu. Here ल् (l) is used as a mnemonic for laghu. However, other conditions may cause such an akṣara to be treated as a guru, as specified by the next two sūtras.

The above sūtra forms a typical example where anuvṛtti is required to understand the content of the sūtra. The term anuvṛtti means re-use of or borrowing something mentioned earlier without explicitly mentioning it again, in order to be concise. In this case, ल् (l), indicating laghu, is borrowed from the previous sūtra. The letter ग् (g) is the mnemonic for a guru. Thus, the sūtra essentially conveys that the laghu akṣara occurring at the end of a quarter of a verse should be treated as a guru. This sūtra is a general rule, exceptions to which are discussed later by Halāyudha.

Here, both l and g are borrowed from the previous sūtras. The akṣara dhra signifies a conjunct consonant. The word ādi (etcetera) extends the rule to a laghu followed by an anusvāra or a visarga or a consonant ending as well.

There is an anuvṛtti of the g (guru) from the last but one sūtra. Though the mnemonic g for guru was introduced earlier, it is only in this sūtra that it gets defined.

In summary, the rules for determining what constitutes a guru akṣara boil down to the following:

1. The akṣara is in itself a long vowel or possesses a long vowel.
2. The akṣara has an anusvāra or visarga or ends in a consonant.
3. The akṣara is followed by a conjunct consonant.
4. At the end of a pāda, an akṣara with a short vowel can be optionally taken as a guru.

All other akṣaras are to be considered laghu. These rules are captured in the following verse by Kedārabhaṭṭa [7, 1.9]:

सानुस्वारो विसर्गान्तो दीर्घो युक्तपरश्च यः ।
वा पदान्ते त्वसौ ग्वक्रो ज्ञेयोऽन्यो मात्रिको ऌजुः ॥

sānusvāro visargānto dīrgho yuktaparaśca yaḥ ।
vā padānte tvasau gvakro jñeyo’ nyo mātriko ḷjuḥ ॥

Piṅgala then goes on to give the relation between guru and laghu in the next sūtra.

Here, ‘that’ refers to guru alluded to in the previous sūtras. Thus, the above sūtra states that two laghus are equivalent to one guru. Another way of stating this is that a laghu is equivalent to one mātrā and a guru is equivalent to two laghus, i.e., two mātrās. As per the convention used by both Halāyudha and Kedārabhaṭṭa, a guru is indicated by a curvy line while a laghu is indicated by a straight line as shown in the table below. We will use the same convention henceforth in this article.

Akṣara	Notation
laghu	।
guru	ऽ

 

An example

For the following verse from the gola section of Āryabhaṭīya [6, p. 118], we have marked each akṣara as guru or laghu based on the rules discussed above. The explanation as to why a particular akṣara has to be considered as a guru or a laghu for the first few words are provided in the subsequent table. We encourage the readers who are not quite conversant with these concepts to undertake a similar exercise for the remaining words in the verse.

               
yadvat kadambapuṣpagranthiḥ pracitaḥ samantataḥ kusumaiḥ।
tadvaddhi sarvasattvaiḥ jalajaiḥ sthalajaiśca bhūgolaḥ ॥

Just as the bulb of a kadamba flower is covered all around by blossoms, so too the globe of the Earth is surrounded by all creatures (sattvaiḥ), terrestrial as well as aquatic.

Akṣara	Type	Reason
य = य्+अ	ऽ	Followed by the conjunct consonant द्व (dva) = द् + व
द्वत् = द्+व्+अ+त्	ऽ	Akṣara ends in a consonant.
क = क्+अ	।	Contains only a short vowel. Also not followed by anusvāra, visarga, conjunct consonant, nor ends with a consonant.
द = द्+अ	ऽ	Followed by the conjunct consonant म्ब (mba) = म् + ब
म्ब = म्+ब्+अ	।	Does not satisfy any of the conditions for a guru akṣara.
पु = प्+उ	ऽ	Followed by the conjunct consonant ष्प (ṣpa) = ष् + प
ष्प = ष्+प्+अ	ऽ	Followed by the conjunct consonant ग्र(gra) = ग् + र
ग्र = ग्+र्+अ	ऽ	Followed by the conjunct consonant न्थिः (nthiḥ) = न् + थिः
न्थिः = न्+थ्+इ+ः	ऽ	Followed by a visarga.

 

Types of metres

Halāyudha in his commentary quotes the following verse which classifies the metres employed in the classical literature (as opposed to the Vedic corpus) into three types of metres [1, p. 46]:

आदौ तावद्गणच्छन्दो मात्राछन्दस्ततः परम् ।
तृतीयमक्षरच्छन्दश्छन्दस्त्रेधा तु लौकिकम् ॥

ādau tāvadgaṇacchando mātrāchandastataḥ param।
tṛtīyamakṣaracchandaśchandastredhā tu laukikam॥

The three types of metres mentioned in this verse are:

1. akṣaracchanda: A metre primarily based on the count of akṣaras occurring per quarter of the verse.
2. mātrācchanda: A metre based on the count of the total number of mātrās produced by the guru and laghu occurring in the verse.
3. gaṇacchanda: A metre based on the count of the four-mātrā pattern called the gaṇa occurring in the verse.

Gaṇa

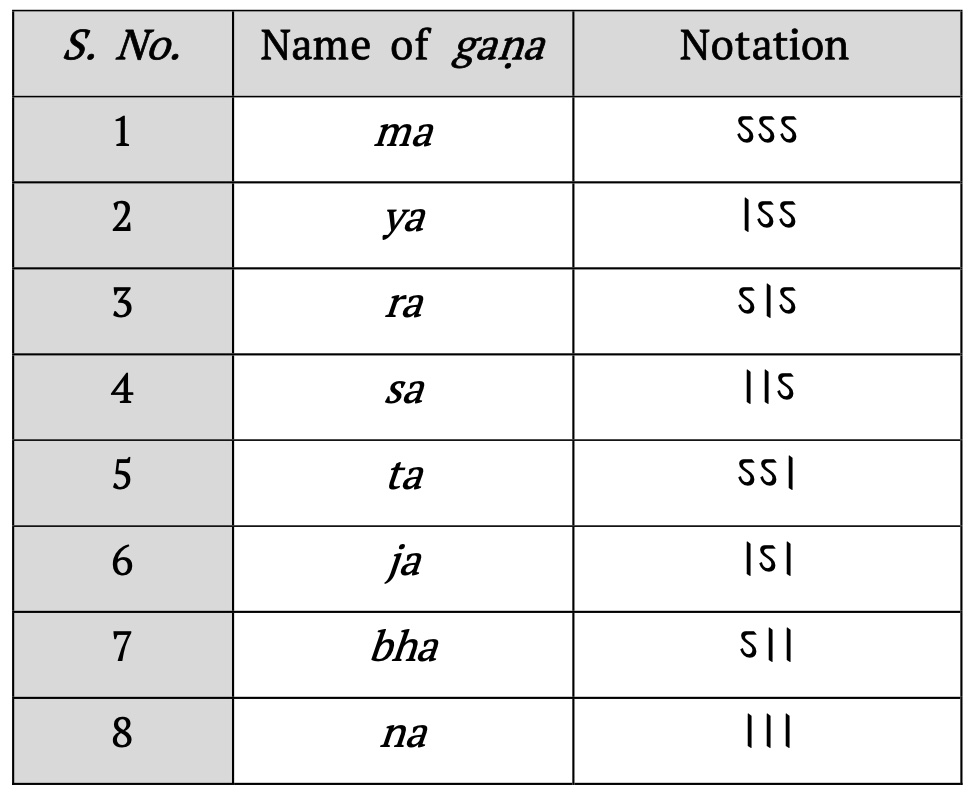
The term gaṇa literally means ‘group’. It can be a group of akṣara or a group of mātrās. In the context of akṣaracchanda, a gaṇa refers to a group of three akṣaras. Since each akṣara could either be a laghu (one mātrā) or a guru (two mātrās), this gives rise to 2^3=8 possible gaṇas. Piṅgala lists these gaṇas in the first eight aphorisms of the Chandaśśāstra [1, 1.1–8]. These akṣara-based gaṇas, starting with all gurus and ending with all laghus, are listed in Table 1.

In the context of gaṇacchanda, Piṅgala defines a gaṇa with the following sūtra:

The word samudrā here refers to the number four.³ Thus, the sūtra, by stating that four laghus form a gaṇa essentially indicates that four mātrās form a gaṇa. Piṅgala then goes on to list the five possible ways in which a mātrā-gaṇa can be constructed by the following sūtra:

Recall that the word na-gaṇa here refers to one of the eight akṣara-based gaṇa patterns in the classification listed in Table 1. The five (and only five) possibilities of forming the mātrā-gaṇas are listed in Table 2.

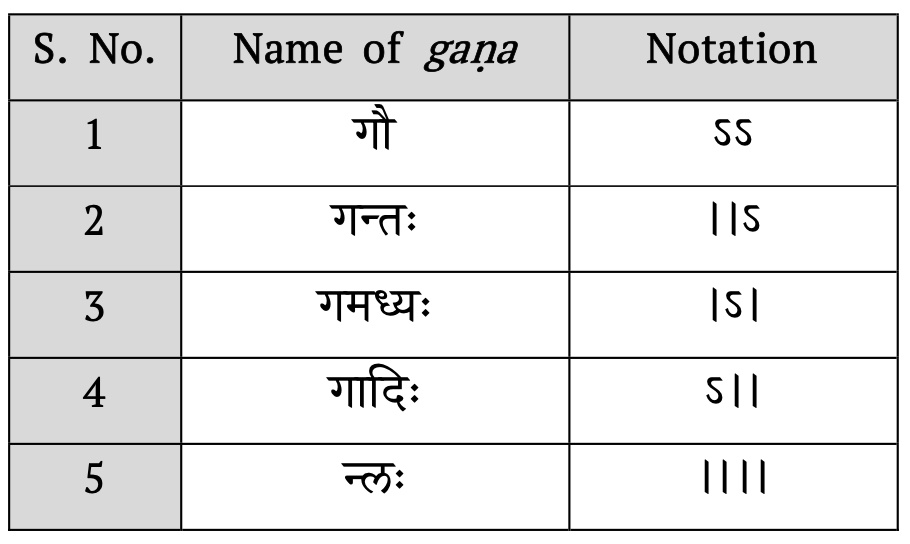
The āryā metre, which will be the focus of the rest of this article, is classified as a gaṇacchanda. Thus, the term gaṇa is to be interpreted as equivalent to four mātrās for the rest of this article, unless otherwise stated.

The āryā metre

Having presented these definitions, Piṅgala proceeds to define the āryā metre with the following sūtra:

The word svarā here stands for the number seven, using the bhūtasaṅkhyā system. The word gaṇa is borrowed from the earlier sūtras. Since one gaṇa is equivalent to four mātrās, this means that the [first] half of a verse in the āryā metre should have the equivalent of 7.5 \times 4=30 mātrās. Halāyudha further states that second half of the āryā is similar to the first half but as we shall see soon, there are a few more constraints to this.

Further elaborating on the definition of the āryā metre, Halāyudha brings forth another interesting feature that needs to be kept in mind while studying this metre:

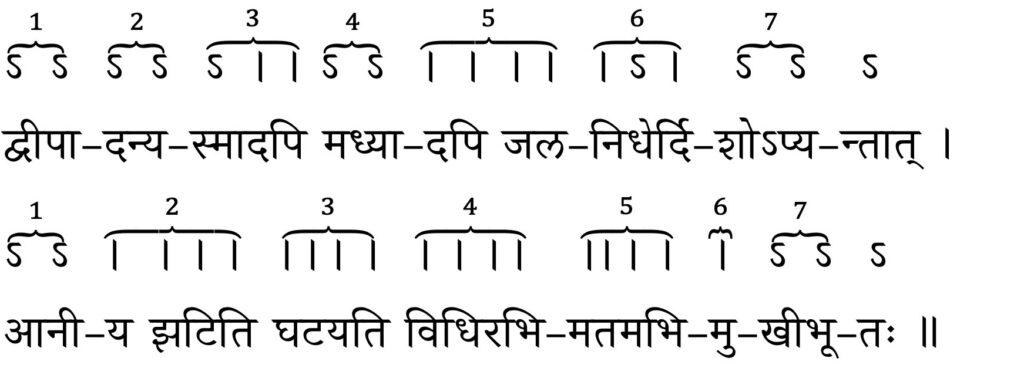
The following verse is given by Halāyudha [1, p. 48] as an example in order to illustrate the definition of the āryā metre:

dvīpādanyasmādapi madhyādapi jalanidherdiśo’pyantāt।
ānīya jhaṭiti ghaṭayati vidhirabhimatamabhimukhībhūtaḥ॥

Providence (vidhi) will fetch the environment (ānīya) from another island (dvīpādanyasmāt), from the centre of the ocean (madhyādapi jalanidheḥ), or from the far end of the opposite direction (diśo’pyantāt) and connect you to what it desires (abhimatam).

Here, as well as in the following verses, we have deliberately introduced hyphenation in the words to facilitate an easy comprehension of the various gaṇas that form the āryā metre. It may be noted that in the second half of the verse, the sixth ‘gaṇa‘ has been marked as just a single laghu (one mātrā) and not four mātrās. Piṅgala explains this in sūtra 4.21 which we will take up shortly. Thus, the second half of the āryā metre [generally] has 27 mātrās as opposed to 30 mātrās in the first half. Piṅgala next proceeds to explain in a few sūtras, further constraints on the gaṇas that have to be observed while composing a verse in the āryā metre.

Constraints on the gaṇas of the āryā metre

After stating the definition of the āryā metre, seven sūtras have been laid down by Piṅgala to explain the various constraints that have to be considered while composing verses in this metre. The first of these seven goes as:

One can readily verify that the first, third, fifth and seventh gaṇas are not ja-gaṇa (।ऽ।) in either half of the example verse given above. The next sūtra places a restriction on the sixth gaṇa.

This can also be readily verified for the first half of the verse quoted above. Halāyudha gives another illustration [1, p. 48] which also can be seen to satisfy all the conditions listed so far for the āryā metre.

sā jayati jagatyāryā devī divamutpatiṣṇuratirucirā।
yā dṛśyate’mbaratale kaṃsavadhotpātavidyudiva॥

There is another point that is illustrated here. Note that the last akṣara of the verse, व va), is marked as a guru, making use of the flexibility to treat the last laghu of a pāda as a guru even though a pāda is not strictly defined for the āryā metre. In the next sūtra, Piṅgala allows one more possibility for the sixth gaṇa.

The reference to the sixth gaṇa is borrowed from the previous sūtra. The term nlau signifies a combination of a na-gaṇa with a laghu. This means that the sixth gaṇa may also be of the form of four explicit laghus. In such a case, a further constraint has been laid down by the following sūtra:

Halāyudha illustrates this with the following example [1, pp. 48–49]:

rūpāntareṇa devīṃ tāmeva staumi sapadi kila mahiṣaḥ।
pādasparśasukhādina mīlitanayano’bhavadyasyāḥ॥

In the above example, the word sapadi does indeed start at the second of the four laghus that constitute the sixth gaṇa in the first half of the verse. A similar constraint for word beginnings is also applicable if the seventh gaṇa is made of four laghus. The rule laid down is:

The following example [1, p.49] is presented for this situation:

brahmakṣatrakulīnaḥ samasta sāmantacakranutacaraṇaḥ।
sakalasukṛtaikapuñjaḥ śrīmān muñjaściraṃ jayati ॥

Here the new word nutacaraṇa starts at the first akṣara of the seventh gaṇa.
Now, Piṅgala moves on to specify the rules for the second ‘half’ of the āryā metre.

The example below [1, p.49] illustrates this rule.

sa jayativākpatirājaḥ sakalārthimanorathaikakalpataruḥ।
pratyarthibhūtapārthivalakṣmīhaṭhaharaṇadurlalitaḥ॥

As can be seen, the fifth gaṇa in the second half has four laghus and the word haṭhahara begins at the first akṣara of this gaṇa.

A restriction is now imposed on the sixth gaṇa in the second half of an āryā verse.

The reference to the second half of the verse is borrowed from the previous sūtra. We have already seen this formulation of the sixth gaṇa in the second half of an āryā verse in all the examples quoted so far.

All the constraints to be fulfilled in an āryā verse are captured by Kedārabhaṭṭa in the following two verses [7, 2.1, 2.2] which are themselves composed in the āryā metre, thereby demonstrating its various features:

lakṣmaitat sapta gaṇā gopetā bhavati neha viṣame jaḥ।
ṣaṣṭho’yaṃ nalaghū vā prathame’rdhe niyatamāryāyāḥ॥

ṣaṣṭhe dvitīyalāt parake nle mukhalācca sayatipadaniyamaḥ।
carame’rdhe pañcamake tasmādiha bhavati ṣaṣṭho laḥ॥

These two verses nicely summarize the rules to be observed while constructing verses in the āryā metre:

1. One half of the verse should have seven and a half gaṇas. That is, seven gaṇas followed by a guru. However, in the other half, the sixth gaṇa is just a laghu, i.e., it is not a regular 4-mātrā-gaṇa, but just has one mātrā.⁴
2. The odd (viṣama) gaṇas cannot be ja-gaṇa (।ऽ।).
3. The sixth gaṇa (in the first half) can be a ja-gaṇa (।ऽ।) or a combination of na-gaṇa (।।।) with a laghu, referred to as nalaghū in the above verse.
4. If the sixth gaṇa is in the nalaghū (।।।।) form, then a new word should begin at the second of these laghus.⁵
5. If the seventh gaṇa of the first half is of the nalaghū form, then a new word should begin at the first of these laghus.⁶
6. If in the second half (carame´rdhe) of an āryā verse, the fifth gaṇa is of the nalaghū form, then also a new word should begin at the first of these laghus.⁷

Possible variations in āryā verse are 8,19,20,000!

Nārāyaṇa Bhaṭṭa in his commentary on the Vṛttaratnākara, called the Nārāyaṇī, has presented a couple of verses [8, p. 45] that enable us to determine the number of ways in which an āryā verse could be constructed. These two verses are also in the āryā metre, in its pathyā and upagīti forms respectively, about which we shall discuss in the article subsequently.

जगणविहीना विषमे चत्वारः, पञ्च युजि, चतुर्मात्राः ।
षष्ठे द्वाविति च गणाः तथाङ्कतः प्रथमदलसङ्ख्या ॥

एवमपरार्धसङ्ख्या षष्ठे स्याल्लघुनि चैकस्मिन् ।
आर्यासङ्ख्योभयदलसङ्ख्याधाताद्विनिर्दिष्टा ॥

jagaṇavihīnā viṣame catvāraḥ, pañca yuji, caturmātrāḥ ।
ṣaṣṭhe dvāviti ca gaṇāḥ tathāṅkataḥ prathamadalasaṇkhyā॥
evamaparārdhasaṅkhyā ṣaṣṭhe syāllaghuni caikasmin।
āryāsaṅkhyobhayadalasaṅkhyādhātādvinirdiṣṭā॥

Instead of presenting the translation of the above verses, we shall now straightaway paraphrase their content which would help the reader in quickly appreciating how the multiple possibilities arise. Since the odd (viṣama) gaṇas cannot be ja-gaṇa, they can be formed in only four ways (ऽऽ, ऽ।।, ।।ऽ, ।।।।). The sixth gaṇa in the first half can be formed in two ways (।ऽ।, ।।।।) and in the second half, in only one way (।). The ‘half gaṇa‘ at the end of each half can also be formed in only one way (ऽ). The rest of the gaṇas in the verse can be formed in five ways (see Table 2). These possibilities are listed out in Table 3.

Thus, the total number of variations possible in the āryā (for its pathyā and vipulā forms; see the next section) is given by:
1³ × 2¹ × 4⁸ × 5⁴ = 81920000.

The types of the āryā metre

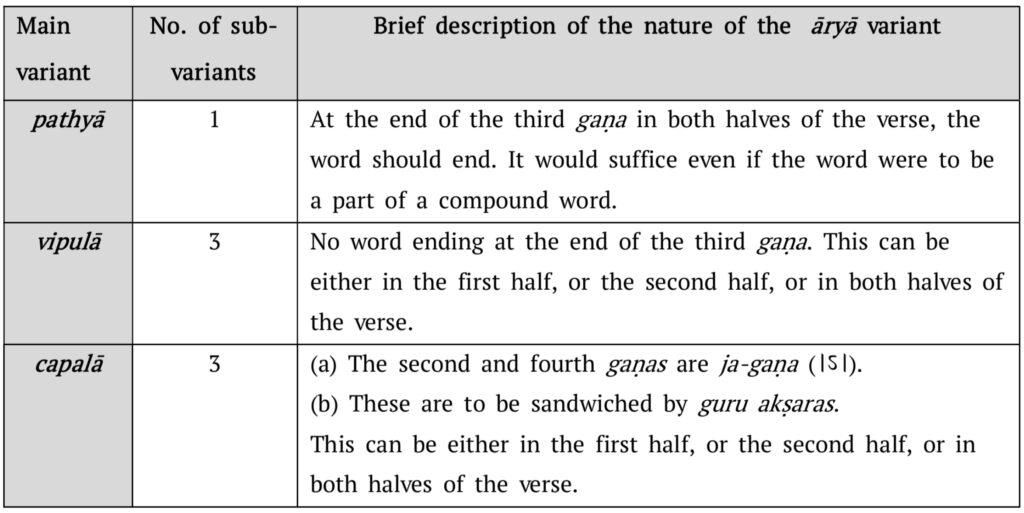
Having defined the āryā metre succinctly in one sūtra [1, 4.14] and subsequently laying down the metrical constraints that are to be observed while composing verses in the āryā metre in seven sūtras [1, 4.15 to 4.21], Piṅgala proceeds to list out three broad categories or types of the āryā that are found in literature. The basis for this categorization into pathyā, vipulā, and capalā is stated in the next three sūtras [1, 4.22 to 4.24].

Pathyā

The reference to the second half of the verse indicated by the word antya continues to be borrowed from sūtra 4.20. The word ca indicates that what is stated is applicable for the first half (ādye) also. The sūtra 4.10 of the Chandaśśāstra (pādaścaturbhāgaḥ) enunciates that the term pāda by default refers to one-fourth of a verse. But in the very subsequent sūtra (yathāvṛttasamāptirvā) it is said that this rule is not a really binding one for all forms of metrical compositions.

With this background we need to understand the term pāda used in the context of an āryā metre. Here it does not refer to exactly one-fourth the number of mātrās in the verse, but just a convenient division after counting three gaṇas. Halāyudha offers the following example of a pathyā āryā verse:

pathyāśī vyāyāmī strīṣu jitātmā naro na rogī syāt।
yadi vacasā manasā vādruhyati nityaṃ na bhūtebhyaḥ॥

One who eats (āśī) healthy food (pathya), performs exercise (vyāyāmī), does not capitulate to women (strīṣu jitātmā), will not succumb to diseases (na rogī syāt). Furthermore, at all times (nityaṃ), and to all beings (bhūtebhyaḥ), he should never hurt either through words (vacasā), or through thoughts (manasā).

This verse is in the pathyā āryā metre because, apart from satisfying the requirements of the āryā metre, in the first half, the word vyāyāmī ends with the third gaṇa, and in the second half the word vā ends with the third gaṇa. Note the profound thought conveyed by this simple couplet and the beautiful alliteration throughout the verse. Also note how the word pathyā has been cleverly incorporated into this example of the pathyā āryā metre. Watch out for this feature in all the examples quoted in this section.

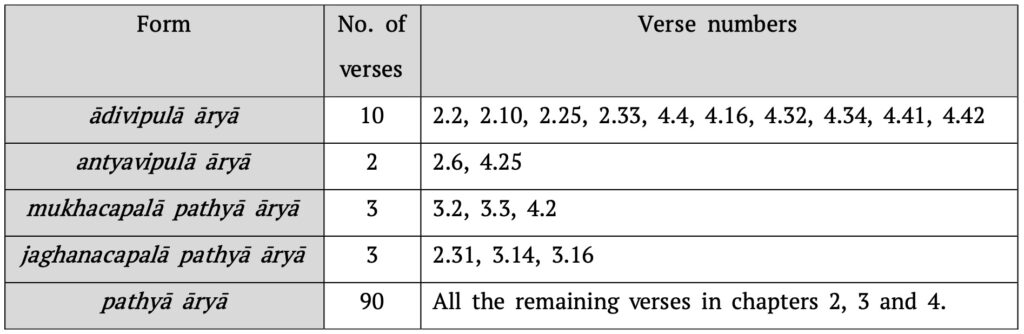
Most of the verses found in the Āryabhaṭīya are of the pathyā āryā form. See Table 6 and Table 7.

Vipulā

If we do not have a word ending at the third gaṇa of an āryā verse, then it is called vipulā. This can happen either in the first half, or in the second half, or in both halves. Depending upon that, the metre is called an ādivipulā, or antyavipulā or ubhayavipulā respectively. Collectively, all such verses are said to be in the vipulā which literally means long, wide, abundant, etc. The nomenclature here is based on the fact that the phrase employed is ‘long’ without a break at the end of the third gaṇa.

Examples [1, p. 50] of the three types of vipulā follow:

strigdhacchāyā lāvaṇyalepinī kiṃcidavanataghrāṇā ।
mukhavipulā saubhāgyaṃ labhate strītyāha māṇḍavyaḥ ॥

In the first half of this verse, the third gaṇa ends in the middle of the word lāvaṇya while in the second half, the third gaṇa ends with the word saubhāgyaṃ. Thus, this is an ādivipulā metre, also known as mukha-vipulā. Also note that in the first half, the sixth gaṇa is formed by four laghus and as per sūtra 4.18, a new word should start on the second akṣara of this gaṇa. Indeed, the word kiṃcid ends and the new word avanata starts at the second akṣara of the sixth gaṇa.

The ādivipulā āryā variant is the second most frequently found metre in the Āryabhaṭīya as can be seen from Table 7.

In this case, the third gaṇa in the first half of the verse ends with the word hariṇī but in the second half of the verse, the end of the third gaṇa falls in the middle of the word vyāja. Hence, this is an antyavipulā metre, also known as jaghana-vipulā. We were able to find only two instances of this metre in the Āryabhaṭīya, namely verses 2.6 and 4.25.

yā strī kucakalaśanitambamaṇḍale jāyate mahāvipulā ।
gambhīramābhiratidīrghalocanā bhavati sā subhagā ॥

In this case, the third gaṇa in the first half ends in the middle of the word nitamba while in the second half it ends in the middle of the word dīrgha, hence, this verse is in the ubhayavipulā metre, also known as mahā-vipulā. We were not able to find any instances of this metre in the Āryabhaṭīya.

Capalā

In order to sandwich the second and fourth ja-gaṇas between gurus, the last akṣara of the first and third gaṇas must be a guru and the first akṣara of the third and fifth gaṇas must also be a guru. Thus, the third gaṇa must be ऽऽ, the first can either be ।।ऽ or ऽऽ and the fifth can either be ऽ।। or ऽऽ.

As in the case of the vipulā, the conditions of the capalā could either be met in the first half of the verse alone (mukha-capalā) or in the second half alone (jaghana-capalā) or in both the halves (mahā-capalā). This is specified in the next three sūtras:

Halāyudha provides examples for each of these cases. Let us consider his example [1, p. 52] of a mukhacapalā verse:

atidāruṇā dvijihvā parasya randhrānucāriṇī kuṭilā ।
dūrātpariharaṇīyā nārī nāgīva mukhacapalā ॥

This verse is a combination of pathyā (since both the halves have a word ending with the third gaṇa of that half) and mukha-capalā (since the second and fourth gaṇas of the first half, but not of the second half, are ja-gaṇas sandwiched between guru akṣaras).

We have found three instances each of the mukha-capalā (verses 3.2, 3.3 and 4.2) and the jaghana-capalā pathyā āryā (verses 2.31, 3.14 and 3.16) metres in the Āryabhaṭīya.

Table 4 summarizes the variants of the āryā metre discussed so far.

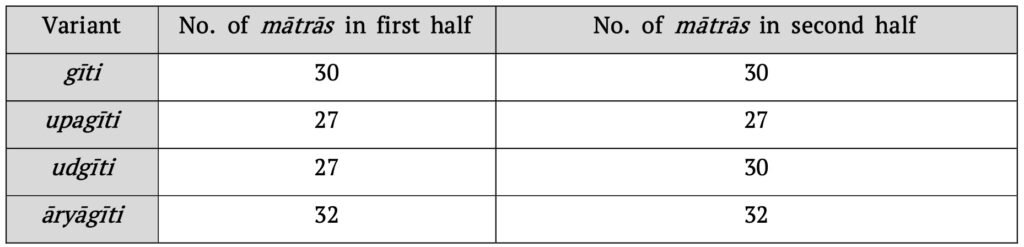
Gīti, upagīti, udgīti and āryāgīti

In the three varieties of āryā discussed so far, there was one common factor. The number of mātrās in the first half and second half was fixed as 30 and 27 respectively. In the four varieties gīti, upagīti, udgīti and āryāgīti that we are going to introduce now, they vary – either in number or in order. In what follows, we introduce these varieties sequentially through the sūtras along with a brief explanation.

Thus, in the gīti metre, the second half of the verse must also have 30 mātrās as opposed to 27 mātrās for the three āryā metres discussed above. Halāyudha further makes it clear that in this case, the sixth gaṇa of the second half must also be either a ja-gaṇa or nlau.

The word antyena in this sūtra, with the borrowing of the phrase ardhasamā from the previous sūtra, essentially amounts to the phrase antyardhasamā, which means `same as the latter half’. Thus, in the upagīti metre, both halves of the verse will have 27 mātrās.

Thus, in the udgīti metre, the first half of a verse has 27 mātrās and the second 30. All the rules applicable to the first and second halves of an āryā are applicable respectively to the second and first halves of the udgīti.

The word vasu here stands for the number 8 (eight) as per the bhūtasaṅkhyā system. Thus, each half of an āryāgīti verse has 8 \times 4=32 mātrās. The other rules of the āryā metre still need to be followed, so the sixth gaṇa in both the halves of the verse must either be a ja-gaṇa or nlau.

The number of mātrās in the first and second halves of the gīti, upagīti, udgīti and āryāgīti variants are summarized in Table 5 below.

The readers can now verify that of the two verses presented in the section discussing the 81920000 variations in āryā verses, the first is in the pathyā āryā form and the second is in the pathyā upagīti form.

Broad categories of āryā metre

An interesting combinatorial exercise may be undertaken at this stage to calculate the total number of categories or forms of āryā at a macro-level by mixing and matching the different forms of this metre that have been discussed so far.

First, we have the pathyā, and then the three vipulā forms. This gives rise to a total of four forms. It may be noted that the pathyā cannot go with any of the vipulā forms since they belong to classes that are incongruent to each other. However, each of these forms could exist either without meeting the capalā conditions or meeting any of the three capalā conditions. Thus, the number of forms becomes 4+(4 \times 3)=16. Now, these 16 possibilities can either have the (30 + 27) mātrā arrangement in the first and second halves respectively, or could be in one of the four further forms, gīti, upagīti, udgīti or āryāgīti. Thus, there could be a total of 16+(16 \times 4)=80 forms of the āryā metre. This is represented pictorially in Figure 1 below.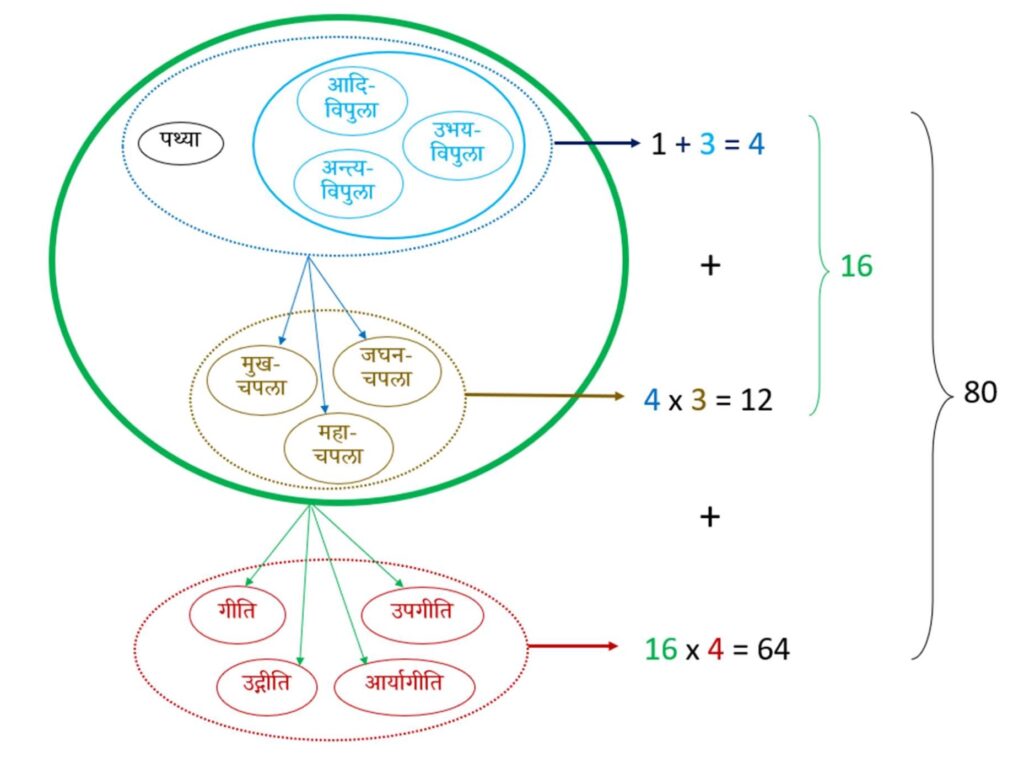

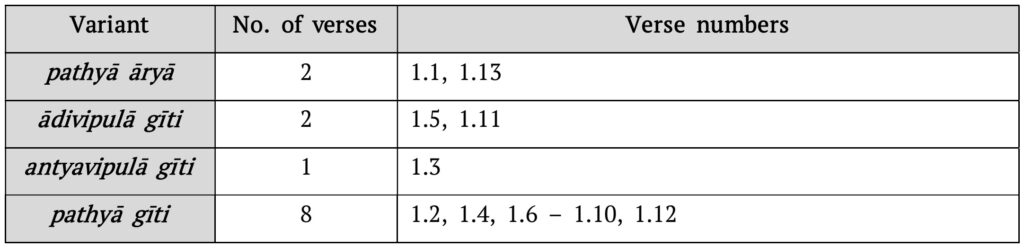
Though most of the verses in the Āryabhaṭīya are in the āryā metre, the first chapter (Gītikāpāda) contains 13 verses of which 11 are in the gīti metre. Of these 11 verses, 8 verses are in the pathyā gīti metre while two are in the ādivipulā gīti metre and one is in the antyavipulā gīti metre (see Table 6). There are no instances of the upagīti, udgīti or āryāgīti found in the Āryabhaṭīya.

Verses from the Āryabhaṭīya

So far, we have demonstrated the rules to be observed while constructing poetry in āryā metre, and its broad variations by considering examples given by Halāyudha in his commentary. We have no clue whether they were examples chosen from classical literature available during his time or they were constructed by himself exclusively for the purposes of demonstration. In any case, these verses did not have any technical content, though they had a lot of literary flavour. In this section we would like to present the readers with a few more examples of āryā metre from a purely technical literature. For this we have chosen the text Āryabhaṭīya, as it is one of the most ancient texts that is extant today. Here we shall demonstrate how the verses in the Āryabhaṭīya comply with the rules of the āryā metre or its variations. Let’s first take up the verse from the gola chapter that was quoted earlier as an example:

yadvat kadambapuṣpagranthiḥ pracitaḥ samantataḥ kusumaiḥ।
tadvaddhi sarvasattvaiḥ jalajaiḥ sthalajaiśca bhūgolaḥ॥

The word puṣpa ends with the third gaṇa in the first half, while the word sattvaiḥ ends with the third gaṇa in the second half. Thus, this is an example of a pathyā form of āryā metre. It may also be mentioned that not only are the rules of prosody adhered to, a beautiful simile is also used to compare the Earth with the kadamba flower.

As mentioned previously, the first chapter of the Āryabhaṭīya, called the Gītikāpāda, is predominantly written in the gīti metre. Let us consider a verse from this chapter (1.5):

kāho manavo ḍha, manuyugāḥ śkha, gatāste ca, manuyugāḥ chnā ca ।
kalpāderyugapādāḥ ga ca, gurudivasācca, bhāratāt pūrvam ॥

A day of Brahmā [or a Kalpa] is equal to [a period of] 14 (ḍha) Manus and [the period of one] Manu is equal to 72 (śkha) yugas. Since Thursday, the beginning of the current Kalpa, 6 (ca) Manus, 27 (chnā) yugas, and 3 (ga) quarter yugas had elapsed before the beginning of the current Kaliyuga [lit. before Bhārata].

This is one of the verses where Āryabhaṭa has employed his unique scheme for number representation. Some of the ‘words’, therefore, do not make any literal sense – they have to be read as numbers. These numbers had to be precisely communicated. Simultaneously, the verse had to comply with the metrical rules. Āryabhaṭa met this requirement by inventing a scheme to represent numbers that allowed him sufficient freedom to be able to communicate the exact number while adhering to the requirements of the metre.

This verse is in the mukhavipulā form of the gīti metre. This is because, in the first half, the third gaṇa ends in the middle of the word yugāḥ while in the second half, the third gaṇa ends with the complete word pādāḥ. Further, note that in the first half, the sixth gaṇa is formed by four explicit laghus. Sure enough, a new word, manu, begins at the second of these four laghus.

Let us consider one more example from the second chapter (2.31) called the Gaṇitapāda which presents various mathematical formulae:

bhakte vilomavivare gatiyogenānulomavivare dvau ।
gatyantareṇa labdhau dviyogakālāvatītaiṣyau ॥

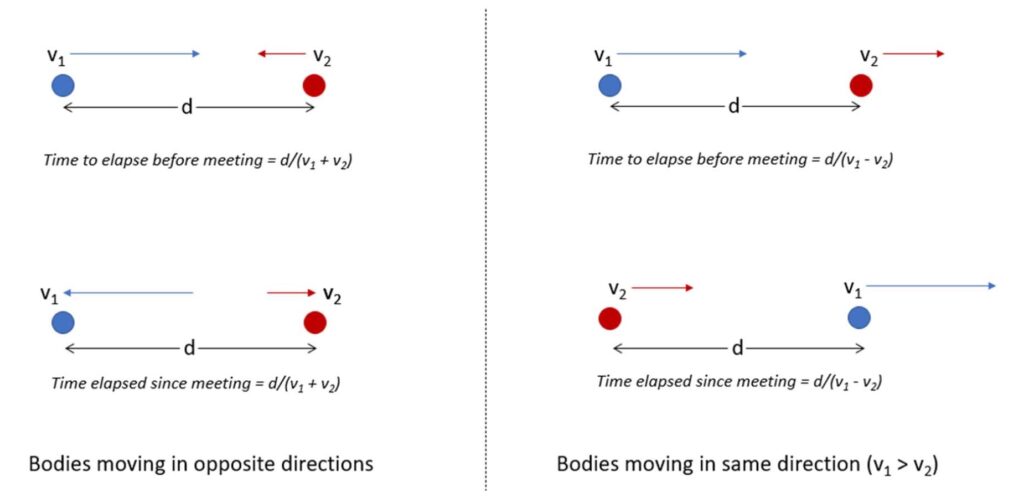
Divide the distance between the two bodies moving in opposite directions by the sum of their speeds, and the distance between the two bodies moving in the same direction by the difference of their speeds; the two quotients will give the time elapsed since the two bodies met or to elapse before they will meet.

This verse essentially presents different formulae that would be found very useful while studying the motion of objects that are moving with different speeds (velocities). The motion could be along a straight line or in a circle. The latter is particularly important in astronomy since we are interested in finding the synodic period, particularly between the sun and the moon, which gives us the duration of the lunar month.

Considering two bodies moving with velocities v_1 and v_2 (assuming v_1 > v_2) and using the concept of relative speed, the verse presents formulae for the time that has elapsed since their meeting or time required for them to meet, once the distance between them is known. If d be the distance between the bodies at time t=0, then the time required for them to meet, or that has elapsed since their meeting, is given by

\[\begin{align*} T &= \frac{d}{v_1+v_2} {\text{(if moving in opposite directions)}}\\
T &= \frac{d}{v_1-v_2} {\text{(if moving in same direction)}}\end{align*}\]These two situations are schematically depicted in Figure 2.

For this verse too, it is very easy to verify that all the metrical requirements of the āryā metre are fulfilled. Further, in both the halves, we have a word ending at the end of the third gaṇa (vivare in the first half and labdhau in the second half). Finally, the second and fourth gaṇas in the second half are ja-gaṇas and both have gurus on either side of them. Thus, this verse is an example of the jaghana-capalā-pathyā-āryā metre.

Table 6 lists the type of verses found in the Gītikāpāda, the first chapter of the Āryabhaṭīya, as per the analysis done by the authors.

All the verses in the remaining three chapters of the Āryabhaṭīya are exclusively composed in the āryā metre. Table 7 lists the forms of the āryā metre that may be found in these verses.

Some interesting cases

Āryabhaṭa concludes the first chapter of the Āryabhaṭīya with the following verse (1.13):

daśagītikasūtramidaṃ bhūgrahacaritaṃ bhapañjare jñātvā ।
grahabhagaṇaparibhramaṇaṃ sa yāti bhitvā paraṃ brahma ॥

Knowing this daśagītika-sūtra [giving] the motion of the Earth and the planets, on the celestial sphere [sphere of asterism of bhagola], one attains the supreme Brahman after piercing through the orbits of the planets and stars.

Though the chapter contains thirteen verses, Āryabhaṭa refers to ten gīti sūtras only. It may further be noted that this thirteenth verse itself is not in the gīti metre, but rather in the pathyā āryā metre. The invocatory first verse of this chapter is also not in the gīti metre. This still leaves eleven verses in the chapter which are in the gīti metre.

Puzzle of the extra verse

Which additional verse Āryabhaṭa meant to leave out in his count of ten has been debated by historians. Some scholars have suggested that it is the twelfth verse which is not to be counted as being among the ten gīti verses and they provide several alternative readings of this verse to show how it doesn’t satisfy the gīti metre.

However, it is usually accepted that the second verse of the chapter should be excluded since it just describes Āryabhaṭa’s unique number system, and does not give any information about the sizes and distances of heavenly objects, or time intervals of heavenly phenomena, etc. that would be directly involved with the computation of planetary positions unlike the other ten verses. An interesting summary of this debate can be found in [6, pp. 31–32].

The terse verse: issues and resolution

The twelfth verse of the first chapter, which is referred to as the terse verse [3], presents some complications. In what follows, we shall first highlight the issues and then show how the issue can be resolved.

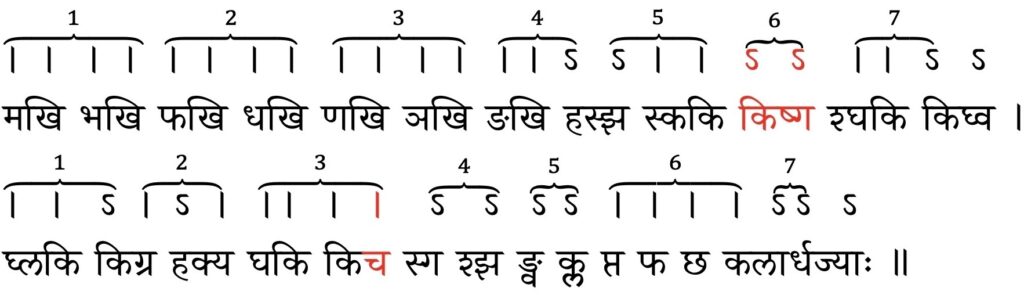
makhi bhakhi phakhi dhakhi ṇakhi ñakhi ṅakhi hasjha skaki kiṣga śghaki kighva ।
ghlaki kigra hakya ghaki kica sga śjha ṅva kla pta pha cha kalārdhajyāḥ ॥

225, 224, 222, 219, 215, 210, 205, 199, 191, 183, 174, 164, 154,143, 131, 119, 106, 93, 79, 65, 51, 37, 22 and 7 – these are the Rsine differences [at intervals of 225 minutes of arc] in terms of minutes of arc.

This verse gives us the equivalent of the modern-day sine tables for angles from 0^{\circ} to 90^{\circ} at intervals of every 3^{\circ}45' (three degrees and forty-five minutes).

At first glance, the verse seems to be in the pathyā-gīti metre. However, there are two issues in terms of the metrical aspects of this verse:

1. The sixth gaṇa of the first half of the verse is neither a ja-gaṇa, nor is it nlau, (i.e., all laghus). Instead, it is composed of two gurus.
2. The ca at the end of the third gaṇa in the second half should be considered a guru since it is followed by the conjunct consonant sga, but has been marked as a laghu here. This indeed is an issue if we go by the general prescription for an akṣara to be considered a guru, which we had laid down in an earlier section.

The first problem could be resolved if the verse is read as:

makhi bhakhi phakhi dhakhi ṇakhi ñakhi ṅakhi hasjha skaki kiṣaga śaghaki kighva ।
ghlaki kigra hakya ghaki kica sga śjha ṅva kla pta pha cha kalārdhajyāḥ ॥

It may be mentioned here that the reading given above has been proposed by the authors of this article. All that has been done is to just introduce the vowel a to two of the consonants. Thus,

ṣ → ṣa and ś → śa

These two minor modifications have done the necessary magic to make the verse fulfil the metrical requirements in the first half that seemed to have gone astray. We surmise that this could be a scribal error that happened at some point of time, which had gone unnoticed for long. Such is the flexibility built into Āryabhaṭa’s number representation system that the numbers implied by these modified ‘words’ remain unchanged in the alternative reading suggested here.

One could now object that a new word is not beginning at the second akṣara of the sixth gaṇa which is now in the nlau form. The counterargument could be that these words, which have no meaning outside of Āryabhaṭa’s unique number representation scheme, are not really words. So, the rules regarding the starting of new words could be ignored when the verse is not having real words.

The second issue seems to be an allowable exception as clearly laid down in the following verse [7, 1.10] from the Vṛttaratnākara:

पादादाविह वर्णस्य संयोगः क्रमसंज्ञकः ।
पुरःस्थितेन तेन स्यात् लघुतापि क्वचिद् गुरोः ॥

pādādāvih varṇasya saṃyogaḥ kramasaṃjñakaḥ ।
puraḥsthitena tena syāt laghutāpi kvacid guroḥ ॥

A conjunct consonant occurring at the beginning of a pāda is called a krama. A guru akṣara occurring before a krama can sometimes be taken as a laghu.

Though there is no strict definition of a pāda in the genre of āryā metres, as per the sūtra (4.22) defining the pathyā metre, we can conceive of pādas even in this genre. Thus, conceiving the above verse to be an example pathyā-gīti, this exception is applicable to our case. It may also be added that the example provided to illustrate this rule in the Vṛttaratnākara is that of an āryā verse [7, 1.11] and the location of the exception, at the end of the third gaṇa in the second half of the verse, exactly matches our case:

taruṇaṃ sarṣapaśākaṃ navaudanaṃ picchalāni ca dadhīni ।
alpavyayena sundari! grāmyajano miṣṭhamaśnāti ॥

In the example above, the fourth gaṇa of the second half of this pathyā-āryā verse starts with the conjunct consonant grā. The preceding akṣara ri should by default (going by the general rule, dhrādiparaḥ in the Chandaśśāstra) be a guru. However, this will upset the metre. In order to take care of such cases, the poetic community has provided the necessary license to treat this akṣara as a laghu and that seems to have been exercised by Āryabhaṭa.

Inbuilt error detection

Consider the following verse (4.27) from the last (gola) section of the Āryabhaṭīya as printed in the edition brought out by Shukla and Sarma [p. 136]:

udayati hi cakrapādaḥ caradalahīnena divasapādena।
prathamo’ntyaścāthānyau tatsahitena kamotkramaśaḥ॥

The first as well as the last quadrant of the ecliptic rises (above the local horizon) in one quarter of a sidereal day diminished by (the ghaṭīs of) the ascensional difference. The other two (viz. the second and third quadrants) rise in one quarter of a sidereal day as increased by the same (i.e., the ghaṭīs of the ascensional difference). The times of rising of the individual signs (Aries, Taurus and Gemini) in the first quadrant are obtained by subtracting their ascensional differences from their right ascensions in the serial order; in the second quadrant by adding the ascensional differences of the same signs to the corresponding right ascensions in the reverse order. The times of rising of the six signs in the first and second quadrants (Aries, etc.) taken in the reverse order give the risings of the six signs in the third and fourth quadrants (Libra, etc.).

The first half of the verse meets all the requirements of an āryā metre. The sixth gaṇa is made of four explicit laghus and a new word begins on the second akṣara of this gaṇa as required. However, there are problems in the second half of the verse. We have a guru instead of a laghu where the sixth gaṇa should have been. Also, the total number of mātrā in the second half is equivalent to only 26 and not 27. Shukla and Sarma have listed several alternative readings for this verse. One of the readings modifies the last word of the verse thus:

udayati hi cakrapādaḥ caradalahīnena divasapādena ।
prathamo’ntyaścāthānyau tatsahitena kramotkramaśaḥ ॥

Not only does this make more sense, it also makes the verse fully compliant with the rules to be met with by the āryā metre.

Here is another example from the kālakriyā section of the Āryabhaṭīya (3.22). See the edition of Shukla and Sarma [pp. 106–108]:

kṣayadhanadhanakṣayāḥ syurmandoccād vyatyayena śīghroccāt ।
śanigurukujeṣu mandādardhamṛṇaṃ dhanaṃ bhavati pūrve ॥

The corrections from the apogee [for the four anomalistic quadrants] are respectively minus, plus, plus, and minus. Those from the śīghraccā are just the reverse. In the case of [the superior planets] Saturn, Jupiter and Mars, first apply the mandaphala negatively or positively [as the case may be].

This verse is clearly in violation of the āryā metre since the fifth gaṇa in the second half of the verse is not well formed. We suggest the following reading of the verse to fix this problem:

kṣayadhanadhanakṣayāḥ syurmandoccād vyatyayena śīghroccāt ।
śanigurukujeṣu mandādardhamṛṇadhanaṃ bhavati pūrve ॥

We found two more cases in the Shukla and Sarma edition of the Āryabhaṭīya where the verses need to be corrected to comply with the āryā metre. The first case is verse 3.23:

मन्दोच्चाच्छीघ्रोच्चादर्धमृणं धनं ग्रहेषु मन्देषु ।
मन्दोच्चात् स्फुटमध्याः शीघ्रोच्चाच्च स्फुटा ज्ञेयाः ॥

mandoccācchīghroccādardhamṛṇaṃ dhanaṃ graheṣu mandeṣu।
mandoccāt sphuṭamadhyāḥ śīghroccācca sphuṭā jñeyāḥ ॥

For this we propose the correction as:

मन्दोच्चाच्छीघ्रोच्चादर्धमृणधनं ग्रहेषु मन्देषु ।
मन्दोच्चात् स्फुटमध्याः शीघ्रोच्चाच्च स्फुटा ज्ञेयाः ॥

mandoccācchīghroccādardhamṛṇadhanaṃ graheṣu mandeṣu।
mandoccāt sphuṭamadhyāḥ śīghroccācca sphuṭā jñeyāḥ ॥

The second case is verse 4.25:

इष्टज्यागुणितमहोरात्रव्यासार्धमेव काष्ठान्त्यम् ।
स्वाहोरात्रार्धहृतं फलमजाल्लङ्कोदयप्राग्ज्या ॥

iṣṭajyāguṇitamahorātravyāsārdhameva kāṣṭhāntyam ।
svāhorātrārdhahṛtaṃ phalamajāllaṅkodayaprāgjyā ॥

The proposed correction is:

इष्टज्यागुणितमहोरात्रव्यासार्धमेव काष्ठान्त्यम् ।
स्वाहोरात्रार्धहृतफलमजाल्लङ्कोदयप्राग्ज्या ॥

iṣṭajyāguṇitamahorātravyāsārdhameva kāṣṭhāntyam ।
svāhorātrārdhahṛtaphalamajāllaṅkodayaprāgjyā ॥

The reader can verify that the corrected verses do indeed comply with the rules of the āryā metre while the original versions do not.

These are classic examples of how non-compliance with the rules of the metre can help us catch inadvertent errors that might otherwise creep in while copying a written work, or when it is transmitted orally.

Conclusion

In the Indian tradition, the knowledge of chandas (metres) is considered to be fundamental to understanding the vedas. It is for this reason that this discipline has been given the status of one of the six vedāṅgas. The importance given to this discipline has been nicely captured in the text Pāṇinīyaśikṣā [4, verse 4.1] with a poetic flavour as follows:

As shown in this article, the understanding and usage of metres was so deep rooted and all pervasive in India that even the mathematical and scientific works needed to be composed in nice poetic metrical form. The linkages between poetry and mathematics in ancient India are not just limited to the use of poetry in writing mathematical texts. Many combinatorial problems naturally arise in the context of the number of variations possible given the restrictions on akṣaras and mātrā in different metres. We saw a glimpse of this when we calculated the number of possible variations of the āryā metre. The last chapter of the Chandaśśāstra is replete with Piṅgala’s exploration of a variety of combinatorial problems including techniques for ranking and un-ranking, the Fibonacci sequence, binary numbers, conversion between binary and decimal numbers, finding the nth power of a number, sum of a geometric series, binomial coefficients, Pascal’s triangle and so on.

The primary aim of this article is to provide the readers an opportunity to understand and appreciate the nuances of the āryā metre which generally remain unknown even to the scholarly community. Incidentally, we also demonstrated how such an understanding helps in detecting and eliminating the errors that would have inadvertently crept into the work due to scribal errors. We also believe that this would help all those previously unaware of the poetic aspects of Indian scientific works and thereby start appreciating these works from this new perspective as well.

acknowledgements The authors would like to sincerely thank the referees for their valuable inputs which have significantly enhanced the quality as well as the readability of the article.\blacksquare

References

• [1] Chandas śāstra by Śri Piṅgalanāga with the commentary Mṛitasañjīvanī by Śri Halāyudha Bhaṭṭa, (Ed. Paṇḍit Kedāranāth) Nirṇaya Sāgar Press, Bombay 1938.
• [2] Filliozat Pierre-Sylvain, The poetical face of the mathematical and astronomical works of Bhāskaracārya, Bhāskara-prabhā, pp. 40–58, (Ed. Ramasubramanian K, Hayashi T, Montelle C), Hindustan Book Agency, New Delhi, 2019.
• [3] Narasimha R, Sines in terse verse, Nature 414, (2001), p. 851.
• [4] Pāṇinīya Śikṣā or The Śikṣā Vedāṅga ascribed to Pāṇini, (Ed. by Manomohan Ghosh), University of Calcutta, Calcutta 1938.
• [5] Ramasubramanian K, Mahesh K, Kolachana A, The līlā of the Līlāvatī, Bhāskara-prabhā, pp. 59–101 (Ed. Ramasubramanian K, Hayashi T, Montelle C), Hindustan Book Agency, New Delhi, 2019.
• [6] Shukla K S, Sarma K V, Āryabhaṭīya of Āryabhaṭa, Indian National Science Academy, New Delhi, 1976.
• [7] Vṛttaratnākara of Sri Kedāra Bhaṭṭa, (Ed. with chandrika Sanskrit and Hindi commentaries by Acharya Baldev Upadhyay), Chaukhamba Surbharati Prakashan, Varanasi.
• [8] Vṛttaratnākaram, (Ed. by Madhusudana Shastri), 2nd Edition, Krishnadas Academy, Varanasi, 1994.

Footnotes

1. See Bhāvanā volume 7, issue 1, January 2023, for a featured article on Pathani Chandrasekhara Samanta. ↩
2. In the case of syllabic metres (akṣaracchanda), a pāda is defined either as one-fourth of the verse or as per the particular syllabic restrictions on each of the four parts into which the metre is divided as per the definition of that metre. This has been stated by Piṅgala through the sūtras, pādaścaturbhāgaḥ and yathāvṛttasamāptirvā [4.10–11]. See also, the subsection titled pathyā. ↩
3. This is based on the bhūtasaṅkhyā system wherein objects are used to refer to numbers. Piṅgala, right at the beginning of his work has indicated that this system of referring to numbers will be used later in the work: aṣṭau vasava iti॥[1, 1.15]↩
4. Usually, the first condition is understood to apply to the first half and the second to the second half and we shall also generally assume the same. But as we shall see later in the article, which condition applies to which half depends on the particular variety of the āryā verse. ↩
5. In the first half of [7, 2.2], the word sayati begins at the indicated position. ↩
6. Again, in the first half of [7, 2.2], the word pada begins at the indicated position. ↩
7. In the second half of [7, 2.2], the word iha begins at the first laghu of the fifth gaṇa. ↩