Moving Frames: Essential Journey of Élie Cartan

Élie Joseph Cartan was born on 9 April 1869, the second of four children, in Dolomieu (Isère), a small village in south-eastern France. His ancestors were peasants. His father, Joseph, was the village blacksmith. As Cartan himself later recalled, Cartan’s infancy was spent serenely. Devotion to hard work, and a marked sense of dignity were his most precious inheritances from his parents. In 1939, on the occasion of the celebration of his 70th birthday, he wrote:

Equally valuable for grooming his character was the influence exerted by teachers at the municipal primary school in Dolomieu. For all his life, Cartan remembered with gratitude and special affection his teachers, Monsieur Collomb, and above all, Monsieur Dupuis. Cartan was an excellent schoolboy since his childhood. Dupuis described him as a shy student whose eyes shone both with the light of intelligence and with the desire for knowledge. His intelligence and almost prodigious memory stood out among all the other pupils in a large class. As Cartan himself was to recall later, he could, without any hesitation, list all subprefectures in each department of France, and remember all the subtlest rules governing the past participle. He was equally skilled in orthography, mathematics, the sciences, history and geography. The young Cartan, Dupuis concluded, understood everything, even before the teacher had finished his lesson.
Dupuis referred his enthusiastic judgment of Cartan to Antonin Dubost (1842–1921) who came to visit the school of Dolomieu in 1878 in his capacity as a cantonal inspector.

Impressed by his potential, Dubost took Cartan’s education to heart and recommended that he apply for a scholarship in a Lycée.¹ Monsieur Dupuis took charge of Cartan’s preparation with unparalleled devotion, which Cartan always recalled with gratitude. A brilliant performance in the examination along with the continuing, fatherly concern of Dubost won Cartan a full scholarship in the College de Vienne. Thus, he left Dolomieu at the age of ten. After five years, his scholarship was transferred to the Lycée de Grenoble, where he devoted himself to classical studies, namely, rhetoric and philosophy. After that, in 1887, Cartan went to the Lycée Janson-de-Sailly in Paris which had only then been recently inaugurated. Among his classmates was Jean Perrin, who was destined to become an eminent French physicist.

Only a year after his entrance to the Lycée, Cartan was admitted to the École Normale Supérieure in 1888. Although his rank at the time of admission was not what one might have expected, his true talent was soon revealed. As Arthur Tresse, one of his friends, was to later recall on the occasion of Cartan’s scientific jubilee, Cartan rapidly took the position that he deserved: the first place in the mathematical section. His opinion in mathematical discussions was highly respected among students; his unremitting diligence becoming almost proverbial. As Tresse himself recounted, Cartan used to sit in the place closest to the entrance door of the reading room. The shorter the path he had to walk, the longer he could stay there to study.

During these years, Cartan was able to attend courses offered by the most prestigious mathematicians in France at that time who had the talent to progress from the most elementary notions of Analysis to the then most recent problems of mathematics. Amongst others, there were Emile Picard, Jules Tannery, Edouard Goursat, Paul Appell, Gabriel Koenigs, Gaston Darboux, Charles Hermite and Henri Poincaré. Cartan remembered with special affection Tannery who seems to have exerted the greatest influence upon his students. Reminiscing, Cartan says:

Lectures by Hermite on elliptic functions and by Darboux on the geometry of curves and surfaces made a big impression on Cartan’s education. He once said about Hermite:

Equally eulogistic were Cartan’s recollections of Darboux who exerted a great influence upon Cartan’s method of moving frames. Cartan wrote:

No less influential were the lectures by Poincaré on electrodynamics which Cartan attended at the Sorbonne. A giant to whom every field of modern mathematics is somehow indebted, as Cartan described him, Poincaré always showed a great interest in Cartan’s career. He seems to have been the first person to recognise the importance of Cartan’s work, even when they were scarcely read and not as widely known. Shortly before his premature death in 1912, Poincaré devoted his last scientific contribution to a survey of Cartan’s already wide mathematical output, and which finally won Cartan due acknowledgement and fame by paving the way to his appointment as a full professor in the Sorbonne in 1912.

Doctoral Dissertation, 1894

Cartan graduated from the École Normale in 1891. Subsequently, he served in the army for one year where he achieved the rank of sergeant. On his return to Paris, Cartan immersed himself in a period (1892–93) of intense study of the structure of (complex) finite-dimensional Lie algebras.

It was during these years of hard work, when he spent most of his time in the library studying papers by Sophus Lie, that Cartan had the occasion to actually meet Lie for the first time. At the invitation of Darboux and Tannery, Lie came to Paris in the Spring of 1893. He had known of Cartan from one of his students, Georg Scheffers, who, in March of the same year, had informed him that a friend of Tresse, whose name was Cartan, was working on a thesis on some of Wilhelm Killing’s ideas. Although, as is observed by Thomas Hawkins in [p. 198 [19]], it appears that Lie’s direct influence on Cartan’s thesis was marginal, but still his meeting with Lie must have been very inspiring. In this respect Cartan wrote:⁵

As Hawkins put it, two main motivations underlying Cartan’s thesis can be distinguished: the discoveries in non-Euclidean geometries and the concomitant reflection upon the foundations of geometry initiated by Bernhard Riemann’s and Hermann von Helmholtz’s works. Indeed, independently of Lie, already in the late 1870s, Killing had developed a notion which turned out to be equivalent to that of a continuous group of infinitesimal transformations (i.e. of a Lie algebra). His concern consisted of providing a classification of the different motions characterising different geometries (space forms in Killing’s language). It was only at a later stage (c. 1884) that Killing, through his correspondence with Felix Klein and Friedrich Engel, discovered that his researches were intimately connected to those of Lie. Indeed, as he soon acknowledged, the set of infinitesimal motions of a given space form could be identified with a continuous group of infinitesimal transformations, in the sense of Lie’s theory.

Despite the fact that he had a clear notion of structure and isomorphism, Lie does not appear to have developed adequate algebraic methods to treat the classification problem of the different isomorphism classes of Lie algebras in their full generality. In this respect, Cartan was more influenced by the theory developed by Killing.

Starting from 1888, Killing, at that time an almost unknown professor at the Lyceum Hosianum in Braunsberg, East Prussia, published a series of four papers titled Die Zusammensetzung der stetigen endlichen Transformationsgruppen [The structure of finite continuous group of transformations] in which he had provided a large part of the essential elements of what in modern terms would be called the “structural theory of complex Lie algebras”. Killing’s approach to continuous groups of transformations was marked by a sharp distinction and contrast with respect to Lie’s, both for its underlying motivations, and also for the technical tools he employed.

The context of Killing’s researches was that of the foundations of geometry, a topic (quite popular in Germany at that time, and) which he had been interested in since 1872 when, in Berlin, he had the occasion to attend Karl Weierstrass’ lectures on the foundations of geometry. Throughout the following years, the problem of classifying all different motions of a given space form attracted his attention, in tune with his general project of classifying all conceivable types of geometries. This led him to develop a structural approach to the classification theory of (complex) continuous groups which, unlike Lie’s more rudimentary treatment, took great advantage of the new trend of rigour initiated by Weierstrass.

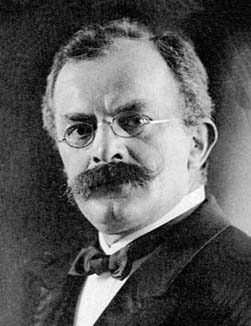
In this respect, the exceptional character of Killing’s activity, among those of other mathematicians trained in Berlin, should be stressed. Possibly as a consequence of his distance from the academic routine, Killing was able to exploit all the advantages (e.g. commitment to rigour and abstract reasoning) stemming from his Berliner education without having to contend with, and also for this very reason too, the skepticism with which Lie’s own work was welcomed there. The result was a fortunate marriage between the Weierstrassian style and Lie’s fertile ideas.

What Lie called a “finite continuous group of transformations” can be described as a set of (analytical) transformations which depend upon a finite number of parameters in such a way that the composition of two transformations of the set is still a transformation belonging to the set itself.

It is important to observe that, independently of the type of space upon which they act, both complex and real groups are included within the definition. Furthermore, one should remark that, contrary to the present day definition, the denomination “finite” refers to the fact that the transformations admit a finite parameterisation in terms of parameters a_1,…,a_r, even if the transformations of G_r are infinite in number.

Besides a wide range of applications, the main objective of the theory was the determination of all essentially distinct transformation groups. One crucial tool introduced by Lie in order to pursue this classification enterprise was the notion of infinitesimal transformation. In Lie’s views, it was the very possibility of characterising the transformation of the group as generated by this type of infinitesimal transformations that justifies the usage of the word “continuous”; as he put it, “a group is called continuous when all of its transformations are generated by repeating infinitesimal transformations infinitely often …”.

The main technical advance introduced by Killing consisted in the prominent role that he attributed to the so-called characteristic equation of a given infinitesimal transformation of a Lie algebra. It is important to note that despite their geometrical motivation, which would have naturally resulted in research on continuous groups with real parameters, Killing limited himself to considering the much easier case of complex Lie algebras.

Killing’s groundbreaking achievements soon stimulated further investigations especially in Paris. As a young, and a most promising student at the École Normale, Élie Cartan decided to devote his doctorate dissertation to the subject of the classification problem of complex Lie algebras.

As a consequence of the general favour with which Lie’s ideas had been welcomed in Paris, many graduate students of the École Normale were encouraged to study Lie’s theory and even to spend some time in Leipzig, where Lie had been teaching higher geometry since 1886, in order to hone their knowledge of the subject. Cartan never went to Leipzig (although he met Lie in Paris), but a close friend of his, Arthur Tresse, did. In particular, it was Tresse who, upon his return to Paris in 1892, informed Cartan of Killing’s research.

Cartan was soon convinced of the importance of taking up Killing’s work with the aim of clarifying some delicate points that, despite Killing’s commitment for rigour, had remained vague. Indeed, as Engel had already pointed out, Killing, en route to his classification enterprise, had relied upon some incorrect statements, that resulted in people questioning the tenability of his approach. Among the many important new results achieved by Cartan in [3], mention should be made of the so-called semi-simplicity criterion, according to which a given Lie algebra can be decomposed into the (direct) sum of simple algebras if, and only if, a certain quadratic form (improperly known as Killing’s form) is non-degenerate.

Exterior Differential Systems

Cartan’s dissertation represented the beginning of a fascinating and highly interesting mathematical enterprise which would eventually lead him to develop a most enterprising approach to differential geometry, known as the method of moving frames. This is a generalisation of the classical techniques of Frenet and Darboux that consisted of attaching moving reference frames to curves and surfaces. The method offers a powerful algorithmic tool for the study of curves and surfaces in different geometrical settings. Cartan’s highly innovative approach in this field was the outgrowth of careful work involving re-interpreting Lie’s classical ideas in the light of new techniques, mainly developed by Cartan himself, of the calculus of differential forms.

Soon after the defence of his doctoral dissertation, Cartan was appointed to the University of Montpellier where he lectured from 1894 to 1896. Then, from 1896 to 1903 he was lecturer in the Faculty of Sciences in Lyon. While in Lyon, he married Marie-Louise Bianconi (1880–1903), a young woman of Corsican origin, who was destined to be Cartan’s beloved wife for his entire life. In 1903, Cartan moved to Nancy, where he became a professor at the local university. In 1904, Henri (1904–2008), the first of four children, was born. Cartan worked in Nancy until 1909 where he also taught Elements of Analysis at the Institute of Electrical Engineering and Applied Mechanics. It was in Nancy, as he recalled years later, that he first got used to addressing a large audience.

These years (1894–1909) of scientific isolation, which were spent away from Paris, the undisputed centre of the French mathematical activity, were nonetheless very fruitful and crucial to the development of Cartan’s mathematical thought. Indeed, it was during these years, that he conceived a great many technical tools which, later on, he would apply to different realms of mathematics, mainly, in differential geometry. It was also during this period that Cartan developed his theory of exterior differential systems, and his peculiar approach to continuous groups of transformations. In his words:

Over the period of a few years after the composition of his doctoral thesis [3], Cartan devoted himself to applications of the theoretical results contained therein. The theory of partial differential equations appears to be one of the main fields of his interest. This emerges quite clearly, for example, from the reading of a dense memoir, [4], dedicated to the theory of those systems of partial differential equations whose solutions depend only upon arbitrary constants and such that they admit a continuous group of transformations. Cartan’s work [5] on Pfaffian forms, and more specifically on the problem of Pfaff was a part of this interest. Indeed, as Lie had demonstrated, the integration of partial differential equations and the integration of Pfaffian forms were considered as equivalent formulations of the same problem.

Cartan starts off by giving a symbolic definition of what a differential expression in n variables is; this is defined as a homogenous expression built up by means of a finite number of additions and multiplications of the n differentials dx_1,…,dx_n as well as of certain coefficients which are functions of x_1,…,x_n. In a similar way, a Pfaffian expression is defined as a differential expression of degree one, and of the following type: A_1dx_1+\cdots+A_ndx_n; a differential form of degree two is given, for example, by A_1dx_2\wedge dx_1+A_2dx_3\wedge dx_2.⁷

A very important notion of Cartan’s new calculus was the exterior multiplication between two differential expressions. Cartan himself observed that already in 1896 he had realised that the change of variables formula in multiple integrals could be easily derived by submitting the differentials under the integration sign, to appropriate laws of calculation, which also incidentally coincide with Grassmann’s exterior calculus. By developing such an intuition, in 1899 he was able to present convincing arguments to justify such rules, which relied upon the idea of the value of a differential form.

To this end, Cartan considered a differential expression \omega of degree h and then supposed that the n involved variables are functions of h arbitrary parameters (\alpha_1,…,\alpha_h). By indicating with (\beta_1, …,\beta_h) one of the h! permutations of the parameters \alpha_1,…,\alpha_h, Cartan associated to it the value that \omega assumes when the differentials occupying the i^{th} (i=1,…,h) position are replaced by the corresponding derivative of x with respect to \beta_i. By attributing to such a quantity the sign + or - depending on the parity of the permutation considered and then by summing over all h! permutations, Cartan finally obtained what he called the value of the differential expression. For example, the value of the differential form A_1dx_2\wedge dx_1+A_2dx_3\wedge dx_2 is:

\[
A_1\frac{\partial x_2}{\partial\alpha_1}\frac{\partial x_1}{\partial \alpha_2}+A_2\frac{\partial x_3}{\partial \alpha_1}\frac{\partial x_3}{\partial \alpha_2}-A_1\frac{\partial x_2}{\partial \alpha_2}\frac{\partial x_1}{\partial \alpha_1}-A_2\frac{\partial x_3}{\partial \alpha_2}\frac{\partial
x_2}{\partial \alpha_1}.
\]

At this point, Cartan defined two differential expressions of degree h to be equivalent if their value is the same, independent of the choice of parameters \alpha_1,…,\alpha_h. In this way he was able to establish Grassmann’s well-known rules of multiplication, but now to be interpreted, in Cartan’s view, as equalities between equivalence classes of exterior differential forms. For example, one has dx_1\wedge dx_2=-dx_2\wedge dx_1 or dx_4\wedge dx_4=0, and it is easy to see this by calculating the values of the differential expressions appearing in the equations.

A second crucial novelty of Cartan’s theory was the exterior derivative of a given Pfaffian expression⁸ which he explicitly connected with Georg Frobenius’ and Darboux’s notion of a bilinear covariant. Cartan’s definition reads as follows. Given a Pfaffian form of type A_1dx_1+\cdots+A_ndx_n, its derived expression was a form of degree two:

\(\omega’=dA_1\wedge dx_1+\cdots+dA_n\wedge dx_n.\)⁹

The invariant character of such derivatives was then established upon reliance on the notion of value by observing that if \bar{\omega} indicates the expression of \omega with respect to a new set of coordinates y(x) then the differential forms of degree two \overline{\omega'} and (\bar{\omega})' are equivalent in the sense specified above.

On the basis of such a new calculus, not only was Cartan able to reformulate all the known results of the theory of Pfaffian equations, including Frobenius’ analytical classification theorem, but he also succeeded in subsequent years (1901–04) in obtaining new remarkable achievements concerning the resolution of general systems of Pfaffian equations (systems in involution).

The main idea at the core of Cartan’s reinterpretation of Lie’s theory was the discovery that the transformations of a given r-parameter continuous group could be characterised as the set of transformations leaving invariant a system of r, properly chosen, differential forms (nowadays, these differential forms are known as Maurer–Cartan forms). Accordingly, Lie’s original approach, which was based upon the notion of infinitesimal transformation, was replaced by a dual perspective that emphasised the role of the invariance properties of differential forms. Although mainly devised to deal with the infinite dimensional generalisation of Lie’s classical notion, the new theory brought important consequences in the realm of finite continuous groups too.

Group Theory by Means of Differential Forms

To give an overview of some of Cartan’s ideas, one can consider a very simple example of continuous group of transformations, given by the affine group of the straight line, for which a direct computation of invariant Pfaffian expressions can be operated in a straightforward way. We consider the set of affine transformations S_{\xi}:X=\xi_1x+\xi_2 and write down the equations of the transformations of the corresponding parameter group:

\[\begin{equation}\label{parametric affine group}
\left\{
\begin{array}{l}
\xi_1’=a\xi_1,\\
\xi_2’=a\xi_2+b.
\end{array}
\right.
\end{equation}\]

The parameters of S_{\xi}^{-1}S_{\xi+d\xi}, which are infinitely close to the identity parameters \xi^0_1=1, \xi^0_2=0, are 1+\frac{d\xi}{\xi},\frac{d\eta}{\xi}. The so-called Maurer–Cartan forms are the forms \omega_1,\omega_2 that measure the difference between the identity parameters and the parameters of the transformation S_{\xi}^{-1}S_{\xi+d\xi}, \xi_1^0+\omega_1, \xi^0_2+\omega_2:

\[
\omega_1=\frac{d\xi}{\xi},\quad \omega_2=\frac{d\eta}{\xi},
\]

And which are immediately recognised to be invariant under the action of (\ref{parametric affine group}).

The usual approach pursued by Lie consisted instead in characterising the transformations S_\xi by means of the infinitesimal transformations that are identified with the analytic vector fields X_1=\dfrac{\partial}{\partial x}, X_2=x\dfrac{\partial}{\partial x}. It should be observed that Cartan’s theory attributed in this way a special role to the parametric group thus favouring the emergence of the notion of an abstract Lie group acting on itself.

In this dual setting, the structure equations [X_1,X_2]=-[X_2,X_1]=X_1 are replaced by the following ones:

\[
d\omega_1=0,\qquad d\omega_2=\omega_2\wedge\omega_1.
\]

Geometrical Investigations

The innovation thus produced did not result in mere technical novelties. On the contrary, it brought in major advancements also on a conceptual level. First, it contributed to the emergence of the abstract notion of a Lie group by placing emphasis on the so-called parameter group rather than on the concrete action of a group upon a manifold. Secondly, it offered a formulation of Lie’s theory which was particularly apt to geometrical applications.

Cartan’s method of moving frames was a development of his peculiar approach to Lie group theory. The main idea consisted in providing a geometrical interpretation of the invariant forms associated to a given group G in terms of the infinitesimal displacements linking together two reference frames.

Cartan’s structure equations d\omega_k=\frac{1}{2}\sum_{ijk}c_{ijk}\omega_i\wedge\omega_j, for k=1,…,r, played an essential role in the application of group theory to geometry. Indeed, a crucial achievement of [7] was the identification of the equations of Darboux’s theory of surfaces treated with the method of moving frames with Cartan’s structure equations of the Euclidean group.

Cartan considered the defining equations of the Euclidean group and deduced from them the structure equations which in this case read as follows:

\[\begin{equation}\label{Euclidean group structure equations}
\left\{
\begin{array}{l}
d\omega_1=\omega_3\wedge\varpi_2-\omega_2\wedge\varpi_3,\\
d\omega_2=\omega_1\wedge\varpi_3-\omega_3\wedge\varpi_1,\\
d\omega_3=\omega_2\wedge\varpi_1-\omega_1\wedge\varpi_2,\\
d\varpi_1=\varpi_3\wedge\varpi_2,\\
d\varpi_2=\varpi_1\wedge\varpi_3,\\
d\varpi_3=\varpi_2\wedge\varpi_1.\\
\end{array}
\right.
\end{equation}\]

The forms \omega_1,\omega_2,\omega_3 and \varpi_1,\varpi_2,\varpi_3 could be interpreted as the components of the instantaneous translation and the instantaneous rotation of the moving trihedra, respectively. In this way, it was easy to recognize that equations (\ref{Euclidean group structure equations}) are equivalent to the equations upon which Darboux had erected his theory of curves and surfaces in Euclidean space.

In the following years, Cartan applied his method of moving frames to a large variety of cases. However, first attempts at systematisation of the theory came only much later, namely in his book [16] which contains a modified version of a set of lectures delivered during the winter semester 1931–32 at the Sorbonne University.

Cartan’s contributions to differential geometry via moving frames can be regarded as a direct outgrowth of his theory of continuous groups which was developed by him in order to handle the infinite dimensional case. As Cartan’s subsequent works would reveal, his own structural approach to group theory turned out to be the most suitable one for investigating more general geometrical theories.

Soon after Einstein’s celebrated series of papers setting out his general theory of relativity appeared, the mathematical community of differential geometers experienced a period of intense activity and reflection upon the mathematical principles at the basis of Einstein’s groundbreaking approach to gravitation and space-time. As is well known, the first manifestation of this phenomenon was represented by the publication of [23] where Tullio Levi-Civita posed himself the problem of investigating the geometrical meaning of Christoffel’s symbols starting from which Einstein had built his celebrated field equations. Therein Levi-Civita showed that an invariant definition of the second-order differentials, which was already to be found in Riemann’s pioneering work, could be geometrically regarded as prescribing the law of parallel displacement of vectors along curves. Accordingly, the curvature tensor was interpreted by him as a direct manifestation of the fact that the (parallel) displacement of a vector depends, in an essential way, on the particular path being considered. Besides, as Levi-Civita proved in full detail, Euclidean geometry could be characterised in terms of absolute displacement in the sense that if the notion of parallelism is independent of the chosen curve connecting two arbitrary points of the manifold, then the curvature vanishes identically. This paper triggered a process of deep reflection upon the state of differential geometry and its relationship with mathematical physics. Once the intrinsic meaning of Riemann tensor had been clarified, a revision of the entire discipline could then be initiated and pursued.

A central topic attracting the interest of physicists and mathematicians consisted in developing a geometrical framework which was sufficiently general so as to offer the possibility of extending the research program pioneered in general relativity, even to the study of electromagnetic interactions. In this respect, Hermann Weyl’s introduction of “infinitesimal geometry”, where a generalisation of Levi-Civita’s parallel displacement was proposed, represented an early outgrowth of such a general tendency.

Cartan’s theory of generalised spaces was part of this widespread interest in searching for new geometrical horizons. Quite interestingly, his first publications on the subject saw the light in 1922, also the year of Einstein’s famous visit to Paris. Nonetheless, it is certain that Cartan’s investigations on generalised spaces date back at least to 1921, as he states in the introduction to [12]. The central aim of this paper was to provide a rigorous proof of the uniqueness, under certain conditions, of Einstein’s choice for the second-order gravitational tensor G_{\mu\nu}. From a technical standpoint, the paper was characterised both by a critical attitude towards Gregorio Ricci-Curbastro and Levi-Civita’s absolute differential calculus, and by a constant recourse to techniques stemming from Cartan’s theory of exterior differential systems, namely his theory of equivalence of G-structures.

This was the context in which for the first time Cartan provided his own reinterpretation of Riemannian curvature in terms of moving frames. By considering a generalisation of the structure equations of the Euclidean group acting on an n-dimensional manifold (variété), Cartan could interpret a Riemannian manifold as a deformed Euclidean space. A measure of such a deformation was given in terms of the so-called curvature 2-forms

\[
\Omega_{ij}=d\omega_{ij}-\sum\omega_{ik}\wedge\omega_{kj}.
\]

More explicitly, in Cartan’s view, \Omega_{ij} was the manifestation of the fact that the structure equations of the Euclidean group cease to constitute a completely integrable Pfaffian system. Since the forms \omega_{ij} represent the components of the instantaneous rotation, it is easily seen that the forms \Omega_{ij} provide an analytical reformulation of Levi-Civita’s above mentioned condition characterising Euclidean space as a Riemannian manifold, endowed with an absolute parallelism.

As for translational components, a similar generalisation was conveyed in [9] where Cartan first introduced a sort of translational curvature which he named “torsion”.

Already in [9], Cartan associated the notion of torsion to non-complete integrability of the Pfaffian equations involving the (infinitesimal) translational components of the group of displacements. Nonetheless, it was in [11] that he provided its analytical expression as follows:

\[
\Omega_i=d\omega_i-\sum_{k=1}^n\omega_k\wedge\omega_{ki}, \quad i=1,…,n.
\]

Curvature and torsion were thus regarded by Cartan as complementary terms which provide a measure of the deformation of the Euclidean space.

A crucial advantage of Cartan’s approach was the generality of the techniques that were being introduced. Indeed, as Cartan explicitly observed, the procedure adopted for the Euclidean group, consisting of deforming its structural equations, could be extended to any continuous group whatsoever (both finite and infinite). As his works to come would soon testify, his method could be generalised in a straightforward way to affine, conformal and projective groups.

It was thanks to Cartan that the notion of continuous group of transformations was investigated on a purely geometrical basis, by translating algebraic properties into the language of connection theory.

Despite the importance of this new standpoint, it should nonetheless be stressed that, at least until 1925, the theory of continuous groups remained a mainly local theory which focused upon the study of transformations close to the identity element. Topological viewpoints into the theory of continuous groups were first introduced by David Hilbert in connection with his celebrated fifth problem concerning the possibility of avoiding the differentiability requirement for functions defining a continuous group. Despite subsequent efforts by Luitzen Brouwer and Otto Schreier, it was only after Hermann Weyl’s seminal works in representation theory that global considerations became an essential part of the discipline, thus preparing the ground for the emergence of the currently accepted definition of a Lie group as a differentiable manifold endowed with a compatible group structure.

Back to Paris

In 1909, Cartan moved to Paris where he was lecturer at the Faculty of Sciences in the Sorbonne before obtaining a full professor position in 1912, at the age of 43. Cartan also taught at the École Normale Supérieure where he exercised a great part of his academic activity. Before teaching higher geometry (in 1924, he was appointed to the Chair which had earlier been Darboux’s), he had taught analytical mechanics and potential theory too.

Cartan’s move to Paris marked a turning point in his career. Supported by the enormous applicative potential both of his integration theory of Pfaffian forms and of his structural theory of continuous Lie groups, Cartan’s research interests gradually shifted to the realm of geometry. Still for some years, abstract group theory and the vast field of partial differential equations constituted a driving force for his mathematical activity. Nonetheless, starting from the late 1910s, the analyst and the algebraist rapidly gave way to the geometer.

It was precisely from his contributions to this branch of mathematics, rather than from his previous, almost disregarded achievements, that due acknowledgment for his work finally came. In particular, it was his ground-breaking approach in dealing with generalisations of the notion of space which won him unanimous distinction as an undisputed master of differential geometry.

Though reluctant to build up a mathematical school around himself,¹⁰ it does appear that the influence and the impact which Cartan’s lectures created, both at the Sorbonne and at the École Normale, was deep. Here follows a vivid picture of his teaching qualities sketched by Gaston Julia, on the occasion of Cartan’s scientific jubilee in 1939:

Particularly appreciated was Cartan’s benevolence towards the new generations of mathematicians who saw him as a source of inspiration for their studies. Willing to share his ideas with young researchers, as is witnessed, for example, by his participation in one of the well known Julia Seminars in 1937, still later in his career Cartan was always interested in the most recent changes in mathematics. A young J.A.É. Dieudonné (1906–1992) described this virtue of his character with the following words spoken directly to Cartan:

After more than forty years of academic activity, Cartan retired in 1940. For some years afterwards, he continued his researches, publishing his last mathematical paper in 1949, two years before his death in May 1951.

Over the last years of his long career, numerous acknowledgements for his contributions finally came his way. He received honorary degrees from universities all over the world: from the University of Liege in 1934 and from Harvard University in 1936. In 1947 he was awarded three honorary degrees from the Free University of Berlin, the University of Bucharest and the Catholic University of Louvain. In the following year he was awarded an honorary doctorate by the University of Pisa. He was elected member of the Royal Society of London, the Accademia dei Lincei of Rome and the Norwegian Academy. In 1931 he had already been elected a member of the Academy of Sciences of Paris, to which he was further appointed as president in 1946.

Cartan had erected an enormous mathematical edifice which was destined to exert a deep and long-lasting influence on a disparate number of disciplines: Lie group theory, representation theory, theory of partial differential equations, differential geometry, topology, etc. Ugo Amaldi’s remarks, conveyed on the occasion of Cartan’s commemoration at the Accademia dei Lincei on 14 June 1952, represent a precious description of Cartan’s legacy:

The Epistolary with Albert Einstein

As Langevin aptly observed on the occasion of Cartan’s scientific jubilee, Cartan’s works in the realm of both differential geometry and the theory of exterior differential systems put him in an ideal position to formalise and “to dominate” all mathematical problems posed by Einstein’s theory of gravitation. Soon after the publication of Einstein’s seminal memoirs (1915–16) providing the foundations of the general theory, Cartan began to devote a great deal of attention to the mathematical aspects of both general relativity and unified field theories. The result was an impressive number of papers, memoirs, letters and notes, whose composition was spread over almost twenty years.

Roughly speaking, Cartan’s contributions to this field may be divided into two categories: (1) geometrical applications of the method of moving frames and the theory of equivalence, (2) analytical applications of the theory of differential systems in involution. Cartan’s first paper devoted to relativity theory [8] belongs to the first of these two categories. Therein, after providing his own interpretation of Levi-Civita’s parallel displacement in terms of moving frames, Cartan applied his theory of equivalence (dating back to the early 1900s) in order to show that Einstein’s choice for the gravitational field equations is unique under certain conditions. The problem consisted of proving that every invariant quadratic differential form, which is linear with respect to the second-order derivatives of the coefficients of the metric, can be written as a linear combination of the Ricci tensor, the scalar curvature multiplied by the metric tensor, and the metric tensor itself. The techniques employed by Cartan to prove this fundamental result were most original. Instead of applying the so-called absolute differential calculus of Ricci and Levi-Civita, which he felt did not favour geometrical intuition, Cartan appealed to his theory of equivalent G-structures, with G={\rm SO}(1,3).

In the series of papers Sur les variétés à connexion affine et la théorie de la relativité généralisée Cartan provided for the first time a systematic account of his theory of non-holonomic spaces (generalised spaces) which he regarded as a reconciliation of two distinct geometrical traditions: that of Riemann, founded upon the notion of metric spaces, and that of Klein, founded upon the notion of homogeneity. General relativity (together with Weyl’s attempt to generalise it) served as the main source of Cartan’s inspiration in his search for new geometrical horizons. At the same time, a deepened understanding of the geometrical contents of Einstein’s theory of gravitation provided new insights connected with classical Newtonian gravity. Interestingly enough, Cartan was able to show that in this classical theory, too, gravitation could be interpreted as a manifestation of the non-vanishing curvature of Newtonian space-time.

The liaison with Einstein’s research became even more close and direct over the following years. The first such example is provided by Cartan’s intense correspondence (published in large part in [18]) with Einstein between May 1929 and May 1932. The main topic under discussion was Einstein’s Fernparallelismus, taken as an approach to unified field theories. This new Ansatz, developed by Einstein between the summer of 1928 and the spring of 1931, aimed to provide a general theoretical framework which could encompass both gravitational and electromagnetic fields. From the mathematical standpoint, Einstein’s main innovation was in the idea to achieve this unification by introducing a space-time manifold endowed with absolute parallelism. Unlike Levi-Civita’s parallelism, the geometrical structure obtained in this way was characterised by a space with vanishing curvature and non-vanishing torsion. The components of the torsion tensor were interpreted by Einstein as the fundamental physical quantities at the basis of this theory.

Generalisations of (pseudo) Riemannian geometry in the direction required by Einstein’s Fernparallelismus had already been attempted by many mathematicians. In particular, Cartan was the first to introduce the notion of torsion in the context of his theory of generalised spaces. In fact, his correspondence with Einstein was triggered precisely by Cartan’s concern
that Einstein had overlooked his priority with regard to spaces with absolute parallelism. However, soon after they met in Paris in November 1929, their epistolary exchange turned into a close scientific collaboration.

Cartan provided Einstein with essential mathematical expertise needed in order to address two main issues associated with this new unified field theory. First, how can one determine the system of partial differential equations that provides a truly adequate representation of the physical universe? Second, once one has such a system of differential equations, how can one integrate the system in such a way as to recover solutions compatible with the properties of matter, electricity, gravitational and electromagnetic fields predicted by the theory?

For both of these problems Cartan’s familiarity with the integration theory of general systems of partial differential equations turned out to be essential. Since the early 1900s, he had developed a most innovative approach to partial differential equations that utilised the associated exterior differential systems. Such a strategy had the advantage of being fully independent of the choice of coordinate system. Furthermore, it provided a general theoretical framework which proved to be highly suitable for the analysis of crucial mathematical properties connected with Einstein’s field equations, properties such as compatibility and determinism.

Besides interesting technical aspects, the correspondence between Einstein and Cartan is testimony both to an intimate scientific collaboration and to the recognition of Cartan’s authoritative guide in matters concerning differential geometry and general systems of partial differential equations. Some passages taken from the correspondence offer a most vivid picture of Einstein’s high opinion for Cartan’s mathematical insight. A significant example is provided by the letter that Einstein wrote to Cartan on 16 May 1932:

Some Final Remarks

In discussing French influence on the historical development of mathematics on the occasion of a conference in Belgrade in 1940, Cartan depicted two approaches that have contributed in different and complementary ways to the evolution of mathematics. On one hand there are “those who open royal avenues by coming up with new ideas, usually simple ones but nevertheless ones that have not occurred to anyone else; and those who, on the vast land cleared by the first, till their own gardens, often picking tasty fruits, and sometimes collecting magnificent harvest”.¹⁵ In view of this metaphoric distinction between two mathematical practices, one cannot resist the temptation to ask oneself about the positioning of Cartan’s own mathematical production. It is certainly true that initially–-think, for example, of the classification problem of complex simple Lie algebras–-Cartan’s contribution was that of a patient gardener that trims the imperfections of an untamed forest (namely, Killing’s theory); nonetheless, Cartan’s mathematical trajectory was, by far, the embodiment of the first tendency: an audacious explorer of new routes. This is true in many respects; especially for the technical innovations introduced (exterior differential calculus), but also for the audacity with which he was able to reformulate classical theories such as Lie’s theory of infinite continuous groups, in original and most fertile ways. The revolutionary impact of his ideas in the realm of group theory, especially in differential geometry, can indeed been assimilated to the opening of a brand new research direction that was, and possibly is, in great need of the work of meticulous gardeners. In this respect it is worthwhile to recall the opinion of André Weil who, in a letter addressed to Élie’s son, Henri Cartan (see [p. 6 [26]]), emphasised the demand for commentators on Cartan’s works. Interestingly, he attributed such a need to Cartan’s tendency to work out specific examples with scarce commitment to the formalisation of abstract principles. This is especially true in respect to Cartan’s method of moving frames, as is vividly confirmed for example by Weyl’s review of [16], in which Weyl expressed a mild, and very diplomatic, disappointment for the lack of clarity in the description of general procedures and principles.

One hundred and fifty years after his birth, the understanding of Élie Cartan’s contributions still represents a challenge both for historians and working mathematicians. The extraordinary creative power of his mathematics will continue to provide a most precious source of inspiration for future generations. No doubt, Cartan belongs to the small group of privileged mathematicians whose work can be characterised as “classic”, and takes its veritable position as a cornerstone in the firmament of mathematics.\blacksquare

References

• [1] M.A. Akivis, B.A. Rosenfeld. 1993. Élie Cartan (1869–1951), American Mathematical Society.
• [2] U. Amaldi. 1952. Commemorazione del Socio Straniero Élie-Joseph Cartan, Rendiconti dell’Accademia Nazionale dei Lincei, serie VIII, vol. XII, fasc. 6, 767–773.
• [3] É. Cartan. 1894. Sur la structure des groupes de transformations finis et continus, Première Thèse. Œuvres, 1: 137–287.
• [4] É. Cartan. 1896. Sur la réduction à sa forme canonique de la structure d’un groupe de transformations fini et continu, American Journal of Mathematics, 18: 1–61, Œuvres, 1: 293–253.
• [5] É. Cartan. 1899. Sur certaines expressions différentielles et le problème de Pfaff, Ann. Sci. Éc. Norm. Sup. Paris, 16: 239–332, Œuvres, 2: 303–396.
• [6] É. Cartan. 1901. Sur l’intégration de certaines systèmes de Pfaff de caractère deux, Bull. de la Soc. Math. de France, 29: 233–302, Œuvres, 2: 483–553.
• [7] É. Cartan. 1910. La structure des groupes de transformations continus et la théorie du trièdre mobile, Bull. Sci. Math., 34: 250–284, Œuvres, 3: 145–178.
• [8] É. Cartan. 1922. Sur une définition géométrique du tenseur d’énergie d’Einstein, Comptes Rendus Acad. Sci. 174: 437–439.
• [9] É. Cartan. 1922. Sur une généralisation de la notion de courbure de Riemann et les espaces à torsion, Comptes Rendus Acad. Sci. 174: 593–595.
• [10] É. Cartan. 1922. Sur les éspaces généralisés et la théorie de la Relativité, Comptes Rendus Acad. Sci. 174: 734–737.
• [11] É. Cartan. 1922. Sur les équations de structure des espaces généralisés et l’expression analytiques du tenseur d’Einstein, Comptes Rendus Acad. Sci. 174: 1104–1107.
• [12] É. Cartan. 1922. Sur les équations de la gravitation d’Einstein, Journal des Mathématiques pures et appliquées. (9) 1, 141–204, .
• [13] É. Cartan. 1923. Sur les variétés à connexion affine et la théorie de la relativité généralisée, (prémière partie), Annales scientifiques de l’École Normale Superieure. 40: 325–412.
• [14] É. Cartan. 1924. Sur les variétés à connexion affine et la théorie de la relativité généralisée, (prémière partie) (Suite), Annales scientifiques de l’École Normale Superieure. 41: 1–25.
• [15] É. Cartan. 1930. Notice historique sur la notion de parallélisme absolu, Math. Ann. 120: 698–706.
• [16] É. Cartan. 1937. La théorie des groupes finis et continus et la géométrie différentielle traitées par la méthode du repère mobile, Cahiers Scientifiques, Fascicule XVIII, Gauthier-Villars, Paris.
• [17] S.-S. Chern, C. Chevalley. 1952. “Élie Cartan and His Mathematical Work”. Bull. Amer. Math. Soc., 58: 217–250.
• [18] R. Debever. 1979. Élie Cartan-Albert Einstein. Letters on absolute parallelism 1929–1932, Princeton University Press.
• [19] T. Hawkins. 2000. Emergence of the Theory of Lie Groups, An Essay in the History of Mathematics 1869–1926, Springer-Verlag.
• [20] Jubilé scientifique de M. Élie Cartan célébré à la Sorbonne 18 mai 1939, Gauthier-Villars, Paris, 1939.
• [21] E. Kähler. 1934. Einführung in die Theorie der Systeme von Differentialgleichungen, Teubner, Leipzig.
• [22] W. Killing, Die Zusammensetzung der stetigen endlichen Transformationsgruppen, Math. Ann., 31, (1888), 252–290; 33, (1889), 1–48; 34, (1889), 57–122; 33, (1890), 161–189.
• [23] T. Levi-Civita. 1917. Nozione di parallelismo in una varietà qualunque e conseguente specificazione geometrica della curvatura Riemanniana, Rendiconti del Circolo Matematico di Palermo, 42, 173–205. Also in [IV, 1-39 [24]].
• [24] T. Levi-Civita, Opere Matematiche, 6 Volumes, Zanichelli, Bologna, 1954–1973.
• [25] I. Lisle, G. Reid, Cartan structure of infinite continuous groups, in [pp. 116-145[29]].
• [26] Élie Cartan et les mathématiques d’aujourd’hui, Société Mathématique de France and Centre national de la recherche scientifique, Numéro Hors Série, 1985.
• [27] A. Stubhaug. 2002. The Mathematician Sophus Lie. Springer-Verlag, 373–374.
• [28] H. Weyl. 1938. “Cartan on groups and differential geometry”. Bull. Amer. Math. Soc. 44: 598–601.
• [29] P. Vassiliou, I. Lisle, Eds. 2000. Geometric Approaches to Differential Equations, Cambridge University Press.

---

Endnotes by C.S. Aravinda

The endnotes here are intended to gently guide the interested reader through some of the technical notions appearing in the article, essentially capturing their spirit and meaning, without pretending to be precise with all the finer mathematical nuances involved.

The following words from Chapter 3 of Élie Cartan’s book Leçons sur la géométrie des espaces de Riemann, “[T]he general notion of a manifold is quite difficult to define precisely”, already serve to illuminate the challenge of our task on hand. He adds further, “A surface gives the idea of a two-dimensional manifold. If we take for instance a sphere, or a torus, we can decompose this surface into a finite number of parts such that each of them can be bijectively mapped into a simply-connected region of the Euclidean plane.” We will, therefore, do well to follow the advice of Cartan and stick to examples of surfaces.

The Euclidean plane, together with its component notions of straight lines, triangles, circles, etc. that we come across in high school, is possibly the best example to recall when imagining a surface. It must not have been easy for an early explorer looking around on the surface of our planet to perceive its true shape. The following excerpt from Laura Ingalls Wilder’s Little House on the Prairie, beautifully captures this sentiment:

However, the surface of the Earth, which some early civilisations thought was flat, is now known to be unlike the Euclidean plane. To get an idea of the global image of the surface of the Earth, beyond what we perceive in our immediate vicinity, we come across such notions as maps and atlases in schools, where the precise positional reference of a place is given by its latitudinal and longitudinal coordinates. Rather interestingly, in serious mathematical investigations too, one employs similar notions and terminology to define a manifold in general.

In an informal sense, a manifold is an expanse that locally resembles a small neighbourhood in the Euclidean space in which one moves around. For someone adventurous who walks on a long tight rope stretched between two anchored points, there are only two directions to move–-forward or backward. This is an example of what is mathematically called a one-dimensional manifold. An even more adventurous person, say, a daring sailor on the surface of a deep sea, will have a circle of directions in which to proceed. This is how a typical two-dimensional manifold looks up close. An example of a three-dimensional manifold is the space we live in, where a pilot manoeuvring an aircraft has an extra dimension of freedom to move, like a flying bird.

The lifetime of Élie Cartan (1869–1951) witnessed a remarkable transition from the invention of the aeroplane to a significant knowledge of the shape of our universe. The revolutionary understanding of the abstract geometries brought in by the likes of Gauss, Riemann and Poincaré during the 19th century spurred the physicists of the 20th century to try and gain an understanding of the geometry of the larger universe; the universe in which gravitation of heavenly bodies far greater than that of the Earth and the paths traversed by light from myriad stars necessitated investigations of the so-called four-dimensional space-time, and more generally of a smooth n-dimensional manifold.

A smooth manifold is a space for which the semblance of being locally Euclidean is sharp enough to permit the realisation of all the essential features of differential calculus around any point on it. For example, it will be possible to talk about `smooth curves’ on these objects as well as vectors tangent to smooth curves.

Smooth Manifolds, Metric and Curvature

Formally, a smooth n-dimensional manifold M may be defined¹⁷ as a coherent ensemble of a certain number of pieces, indexed by \alpha, that locally resemble, via appropriate maps \varphi_{\alpha}, a neighbourhood¹⁸ U_{\alpha} in the n-dimensional Euclidean space \mathbb{R}^n. In other words, the following three conditions must be satisfied: (1) M = \bigcup_{\alpha}\varphi_{\alpha}(U_{\alpha}); that is, the whole is the union of its local parts; (2) For each pair of indices \alpha, \beta with \varphi_{\alpha}(U_{\alpha}) \cap \varphi_{\beta}(U_{\beta}) = W(\neq \emptyset), the maps \varphi_{\beta}^{-1} \circ \varphi_{\alpha} and \varphi_{\alpha}^{-1} \circ \varphi_{\beta} between the sets \varphi_{\alpha}^{-1}(W) and \varphi_{\beta}^{-1}(W), called transition maps, are smooth–-that is, are differentiable of any order; and (3) A technical condition (that we shall not bother to elaborate upon) that the collection \{(\varphi_{\alpha}, U_{\alpha}) \}_{\alpha} is maximal, in the sense that any pair (\psi, V) in accordance with conditions (1) and (2) must necessarily be part of this collection.

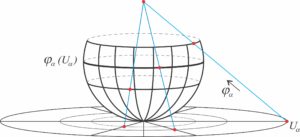
Here is a picture to get an idea of a typical neighbourhood U_{\alpha} in \mathbb{R}^2, the map \varphi_{\alpha}, and the image \varphi_{\alpha}(U_{\alpha}) as a part of the sphere. By moving the line across each point on the lower hemisphere from the north pole, we can associate each point on the sphere with a point that it intersects on the plane.

The next sequence of pictures serves to illustrate the above definition where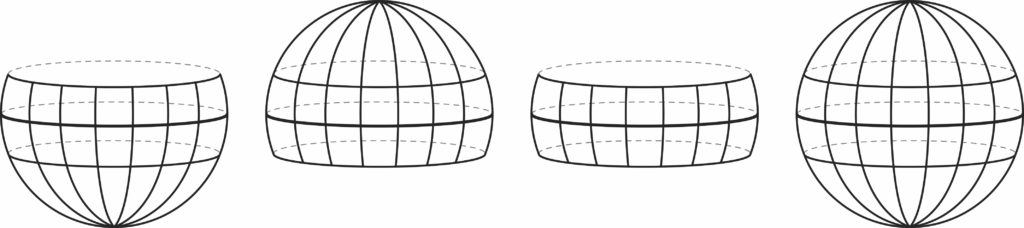

the two individual pieces (or charts) \varphi_1(U_1) and \varphi_2(U_2) are coherently put together to give a global image of the Earth, which is the surface of a sphere. And the intersecting patch W=\varphi_1(U_1)\cap\varphi_2(U_2) is exactly the same as its depiction in either of the two patches \varphi_1(U_1) and \varphi_2(U_2). Using the transition mechanism captured in condition (2) to go from the patch \varphi_1(U_1) to \varphi_2(U_2), and vice-versa, a global study of the Earth becomes possible.

Effectively using this kind of analysis of a surface different from the Euclidean plane, quite like a tailor who stitches together the different pieces of Euclidean planes to create a pair of pants,¹⁹ mathematicians are able to also study more general surfaces such as a torus or a double torus.

The measurement considerations like the lengths of tangent vectors, angles between vectors, and the lengths of smooth curves on a smooth manifold require the introduction of the so-called Riemannian metric. This enables us to look for curves of particular lengths that realise the distance between two points on a manifold, such as the straight lines on the Euclidean plane or certain segments of the latitudes and the equator on the surface of the Earth.

It is intuitively evident that the Euclidean plane is a flat surface (or has zero curvature), whereas the surface of a sphere is evenly curved. The seminal discoveries of Nikolai Lobachevsky and János Bolyai, independently of each other, during the first half of the 19th century helped settle the 2000-year-old problem of Euclid’s parallel postulate, thereby demonstrating the existence of a geometry different from the Euclidean and spherical geometries. This is referred to as the non-Euclidean or hyperbolic geometry. The Riemannian metric further makes it possible to define the important notion of Gaussian curvature of a surface that clearly distinguishes the three geometries.

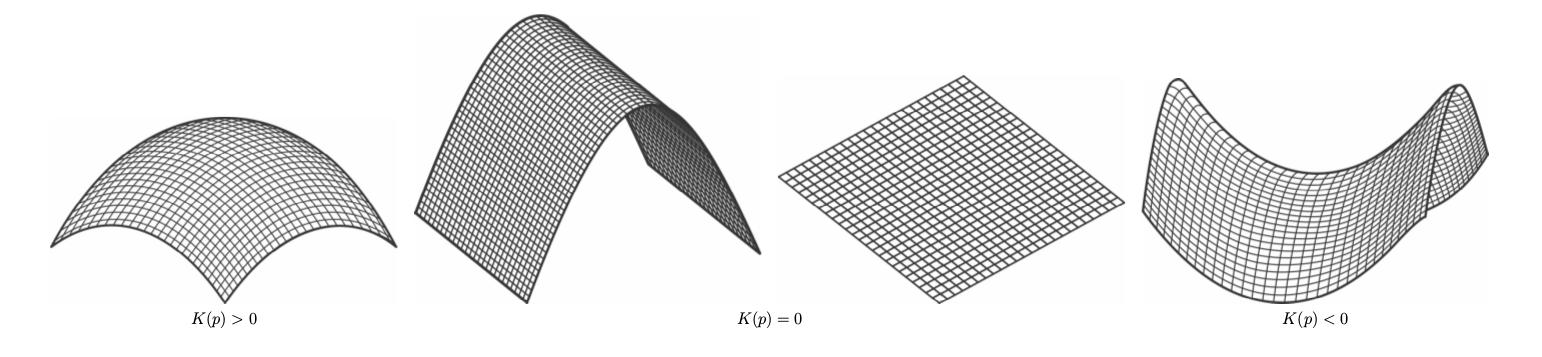
The notion of Gaussian curvature provides information about the different ways the uneven terrain of a surface can bend around. To each point p on the surface, Gaussian curvature is a certain real number K(p), the sign of which, whether positive, zero or negative, tells us about the shape of the surface near the point p, as illustrated above.

Note that in the middle two images portraying zero curvature, there is no angular distortion of the grid lines spanning the surface, although the first of the two is curved in its external appearance. This, in essence, demonstrates the fact that the notion of Gaussian curvature is intrinsic 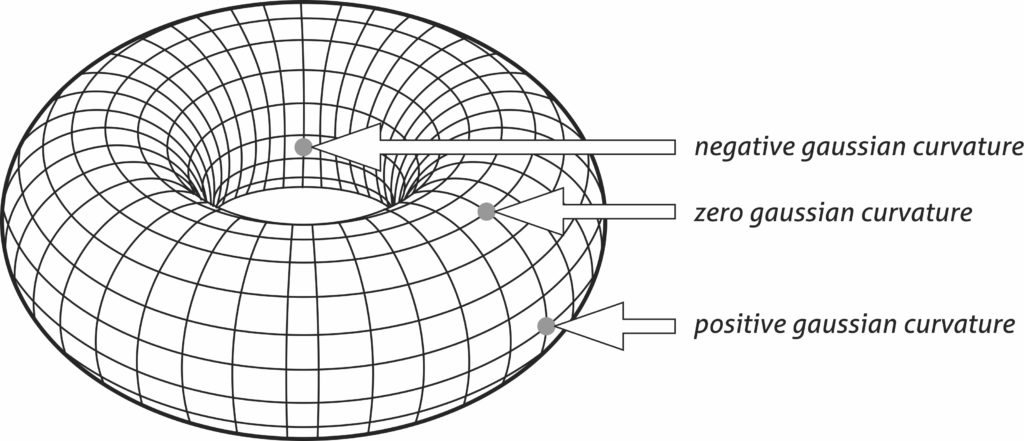to the surface, the discovery of which fact startled Gauss himself, compelling him to call it the “Theorema Egregium” or the “remarkable theorem”.

The surface of a torus, as we view in the three-dimensional space around us, is a classic example where all three signs of curvatures are present at different points.

Tangent Planes, Vector Fields and Differential Forms

The entire collection of tangent vectors of all lengths at a point p and in the circle of directions around it on a surface S is a plane sitting tangentially to S at p, called the tangent plane to S at p, denoted T_pS.

For example, if S is the Euclidean plane \mathbb{R}^2, and the point p = (0,0) is the origin, then the tangent plane at p coincides with \mathbb{R}^2 itself. If p is any point other than the origin, then the tangent plane T_p{\mathbb{R}^2} is simply a shift or translate of \mathbb{R}^2 with point p as the point of reference or the origin of the plane shifted to p. The standard basis of unit vectors e_x and e_y in the x– and y-directions respectively at the origin (0,0), shifted to T_p{\mathbb{R}^2}, is denoted by the symbols \frac{\partial}{\partial x}\vert_p and \frac{\partial}{\partial y}\vert_p.

Whereas if S is the unit sphere S^2 in \mathbb{R}^3, the tangent planes at different points on the sphere smoothly rotate accordingly as points move, and is left as a pleasant exercise to the reader’s imagination to visualise.

The mathematical representation of the effect of a physical phenomenon like the magnetic field around a magnet placed on the surface of a sheet of paper is an example of a vector field. The direction and intensity of the magnetic attraction at a point are indicated by associating a tangent vector of appropriate length and direction at that point.

In general, a vector field on a smooth surface S is the association of a tangent vector to each point on S varying smoothly as does the point. When S=\mathbb{R}^2, the partial derivatives \frac{\partial}{\partial x} and \frac{\partial}{\partial y} are interpreted as the coordinate vector fields that associate to each point p, the tangent vectors \frac{\partial}{\partial x}\vert_p and \frac{\partial}{\partial y}\vert_p. The pair \big\{\frac{\partial}{\partial x},\frac{\partial}{\partial y}\big\} is called the Euclidean frame field.

In a manner similar to that of a vector field, a multivariable specification of an object called the `tensor’ to each point of a surface S is what is known as a tensor field. Of these, certain special types, known as the skew-symmetric covariant tensor fields, are the so-called differential forms. Employing the language of calculus of differential forms, called the exterior calculus, Élie Cartan was able to give a moving frame (or a frame field) description for the geometry of a surface using a special type of differential 1-forms called the connection forms (which he denoted by \omegas). In particular, he showed that the Gaussian curvature function K of a surface S, mentioned earlier, is the unique real-valued function that satisfies the equation d\omega_{12}=-K\omega_1\wedge\omega_2 known as the second structural equation of Cartan; here \omega_{12} is the connection form relevant to the geometry of the surface S, d\omega_{12} is the exterior derivative of \omega_{12}, and \omega_1 and \omega_2 are the two differential 1-forms dual to a frame field.

Having made some sort of a case for their significance in the work of Cartan, let us try to at least know closely what kind of objects differential forms are on the Euclidean plane \mathbb{R}^2.

Mathematically, a differential 1-form associates to each point p in \mathbb{R}^2 a linear map that takes in a tangent vector at p and yields a real number. Thus, at the point p, it is a member of the space dual to the tangent space T_p{\mathbb{R}^2} called the cotangent space T_p^{*}{\mathbb{R}^2}. As an illustrative example, we shall see below how, given a smooth function f on \mathbb{R}^2, one can construct a differential 1-form, denoted by df.

If f is a real-valued, smooth function on \mathbb{R}^2, the partial derivatives \frac{\partial f}{\partial x} and \frac{\partial f}{\partial y} evaluated at a point p give two real numbers. Alternatively, this can be interpreted as the tangent vectors \frac{\partial}{\partial x}\vert_p and \frac{\partial}{\partial y}\vert_p themselves being taken by df–-an object depending only on the function f–-to yield the real numbers \frac{\partial f}{\partial x}(p) and \frac{\partial f}{\partial y}(p) respectively. Furthermore, \frac{\partial}{\partial x}\vert_p and \frac{\partial}{\partial y}\vert_p, being a basis for the tangent space T_p{\mathbb{R}^2}, facilitates extending the above interpretation to all of T_p{\mathbb{R}^2}. That is, if v\in T_p{\mathbb{R}^2} and v=v_1\frac{\partial}{\partial x}\vert_p+v_2\frac{\partial}{\partial y}\vert_p, then df(v)=v_1\frac{\partial f}{\partial x}(p)+v_2\frac{\partial f}{\partial y}(p) defines differential 1-form on \mathbb{R}^2. In particular, df\big(\frac{\partial}{\partial x}\vert_p\big)=\frac{\partial f}{\partial x}(p) and df\big(\frac{\partial}{\partial y}\vert_p\big)=\frac{\partial f}{\partial y}(p). Thus, if x and y are regarded as coordinate functions, then one has the corresponding differential 1-forms dx and dy, called the differential 1-forms dual to the Euclidean frame field \big\{\frac{\partial}{\partial x},\frac{\partial}{\partial y}\big\}. This means that any differential 1-form \phi on \mathbb{R}^2 can be written as f_1dx+f_2dy. In particular, if f is a smooth function on \mathbb{R}^2, then df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy.

A differential 2-form is a skew-symmetric bilinear map that takes in an ordered pair of tangent vectors at each point p in \mathbb{R}^2, and yields real numbers. The meaning of being skew-symmetric is that if the two arguments are repeated, then the value on that pair is zero. Therefore, it is not hard to see that there can be no non-zero differential 3-forms on \mathbb{R}^2. A good example of a differential 2-form is the wedge product of two differential 1-forms. If \phi and \psi are two differential 1-forms on \mathbb{R}^2, p\in\mathbb{R}^2 and if v_1, v_2\in T_p{\mathbb{R}^2}, then their wedge product \phi\wedge\psi is defined by:

\[\begin{align*}(\phi\wedge\psi)(v_1,v_2) = \det\Bigg( \begin{matrix} \phi(v_1) & \phi(v_2)\\ \psi(v_1) & \psi(v_2) \end{matrix} \Bigg).\end{align*}\]

Another example of a differential 2-form is the exterior derivative of a differential 1-form which is defined as follows: Let \phi=f_1dx+f_2dy be a differential 1-form on \mathbb{R}^2. Then its exterior derivative d\phi is the differential 2-form df_1\wedge dx+df_2 \wedge dy.

In mathematics, oftentimes, it becomes imperative to coin novel terminologies, and evolve seemingly terse interpretations of simple facts to reflect on interesting mathematical insights. Also, putting them succinctly in precise language necessitates viewing the same object from several different perspectives. It is quite like working on a delicately balanced piece of architecture that instantly captivates a first-time viewer, both in its form and in its appearance.\blacksquare

Footnotes

1. This is the last stage of secondary education in France, equivalent to classes 10–12 in the Indian school system. ↩
2. See [p. 53 [20]]. ↩
3. See [p. 297 [1]]. ↩
4. Ibidem. ↩
5. Cartan mistakenly put Lie’s visit to Paris in 1892 instead of 1893. Contrary to what Cartan said, Lie’s stay in Paris was only three weeks long. In this respect see [p. 373-374 [27]]. ↩
6. See [p.54 [20]]. ↩
7. Cartan did not employ the wedge product symbol \wedge. ↩
8. The definition was generalised to enclose derivatives of differential forms of degree greater than one in [p. 243 [6]]. ↩
9. The notation d\omega was introduced by Kähler in [p. 6 [21]]. ↩
10. S.-S. Chern and Chevalley in [p. 217 [17]] pointed out that Cartan “had too much of a sense of humour to organise around himself the kind of enthusiastic fanaticism which helps to form a mathematical school”. ↩
11. See [p. 41 [20]]. ↩
12. See [p. 49][20]. ↩
13. See [p. 773 [2]]. ↩
14. See [p. 227 [18]]. ↩
15. See [p. 281 [1]]. ↩
16. See [28]. ↩
17. The formal, mathematically precise definition is attributed to Herman Weyl from his 1913 book Die Idee der Riemannschen Fläche. ↩
18. The word neighbourhood used here has a specific mathematical connotation where it means a set sans its boundary, such as the lower (or the upper) hemisphere excluding the equatorial circle. ↩
19. Indeed, the study of a generic surface by conveniently breaking it up into individual pieces called pair of pants is a method that is widely used in mathematics. ↩