Picking up Indra’s Pearls

The true nature of mathematical discovery

The authors begin the preface with the words:

Indra’s Pearls is a book about serious mathematics, but one which we hope will be enjoyed by as wide an audience as possible.

This book brings to life some of the greatest developments in geometry over the last two hundred years that culminated in Grigori Perelman’s proof of William Thurston’s ‘Geometrization Conjecture’ in 2003 (a year after the publication of this book). It walks the reader through the most basic ideas involved, such as the definition of complex numbers, groups, hyperbolic geometry, topology, fractals, while illuminating them with historically important examples. The book also has historical profiles of mathematicians who contributed to these topics.

The central theme of the book is a game that involves constructing two transformations of hyperbolic space and then applying one or the other in an infinite sequence. The importance of this game comes from the way mathematicians think about geometry, guided by the philosophy of Felix Klein, that geometry is determined by the symmetries that preserve it.

Indra’s Pearls destroys the myth that brilliant mathematicians are mysterious geniuses who simply receive divine words like prophets. It reveals the role of free-wheeling curiosity and persistent experimentation in mathematical discovery. The book invites the reader to not just watch, but also join in this activity. The book is rich with illustrations. Painstakingly produced computer-generated images of group actions are the mainstay of the book. The reader is guided through to drawing these pictures using computer programs, for which pseudocode and hints on implementation are provided. There are open-ended projects meant to encourage the reader to go deeper into the basic ideas and make their own discoveries.

A stick figure man, Dr. Stickler, is used as a simple device to illustrate distortions produced by the transformations that the book explores. There are also cartoons by Larry Gonick, who went on to author publications like The Cartoon Guide to Algebra, The Cartoon Guide to Sex and The Cartoon History of the Universe.

Axiomatics: the beginnings of geometry

The origins of geometry are grounded in the realities of making measurements and understanding shapes on a flat plane, which is a good approximation for the surface of the earth on a human scale.When Euclid axiomatized geometry in terms of points, lines and angles, he was compelled to include an axiom that is now known as the parallel postulate. A version of the parallel postulate can be stated as follows: given a line, and a point not on it, at most one line parallel to the given line can be drawn through the given point.

For two thousand years, mathematicians were unable to decide whether or not this axiom was a logical consequence of the other axioms of geometry. In the first half of the nineteenth century, Carl Friedrich Gauss, Nikolai Lobachevsky and Janos Bolyai (independently) constructed non-Euclidean geometries. These are exotic models for which all the classical axioms of geometry hold, except for the parallel postulate, which fails.

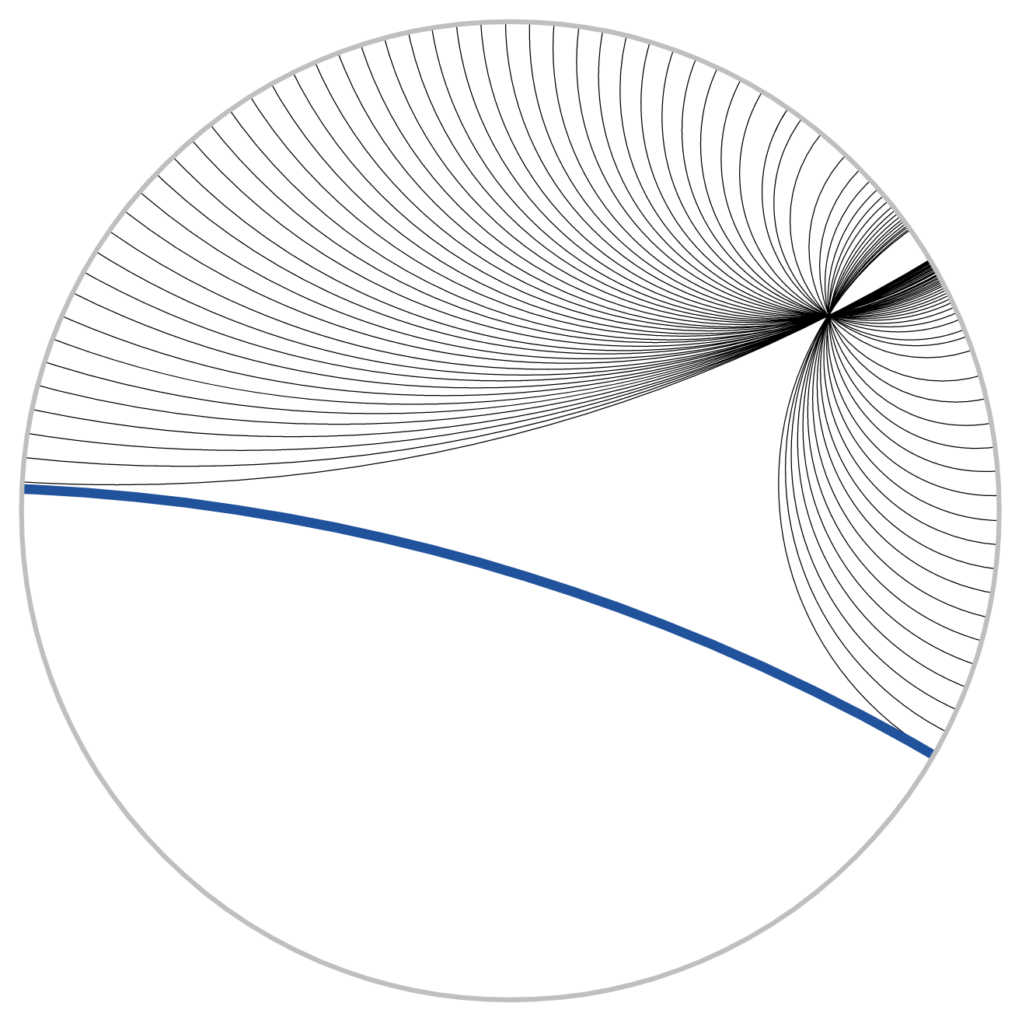
A beautiful realization of such a geometry is Eugenio Beltrami’s Poincaré disc. Its points are the points in the interior of a disc, while its lines are either circular arcs that meet the bounding circle at right angles, or diameters of the bounding circle (see Figure 1). The construction of such geometries demonstrated that the parallel postulate is not a logical consequence of the other axioms of geometry. It also led to a paradigm shift, away from geometry as a means of understanding shapes and distances on a flat surface, to the study of more general systems, via axioms or models. About these developments in the nineteenth century, the authors say in the introduction

Congruence and symmetry

In Euclid’s geometry, two shapes were considered to be equivalent, or congruent, if one could be moved onto the other by a rotation followed by a translation. In particular, every point is congruent to every other, and a pair of points is congruent to another, precisely when the distances between them are equal. The transformations obtained by rotations and translations are the symmetries of Euclidean geometry. Thus, distance, the fundamental invariant of Euclidean geometry, is nicely captured by these symmetries.

In the second half of the nineteenth century, Felix Klein realised that the essence of a geometry lies in its group of symmetries. He went so far as to say that a geometry is just a structure with a prescribed set of symmetries. Symmetries can be thought of as functions from the ambient space onto itself that preserve the structure that is of interest to the geometer. These symmetries (e.g., rotations or translations) are transformations that preserve the structure. The final result of performing one structure-preserving transformation followed by another is once again a structure-preserving transformation called their ‘composition’. Also, the inverse¹ of a structure-preserving transformation is a structure-preserving transformation. Structure-preserving transformations, under the binary operation of composition, form an algebraic structure that is called a group.

Groups first arose in the 1830s, when Evariste Galois exploited the group of symmetries of the roots of a polynomial equation to understand their true nature. He related the solvability of the polynomial equation by radicals to the abstract structure of this group of symmetries. Here, abstract structure means that the group is viewed only as a set with a binary operation. That it is a group of symmetries of the solutions of an equation is forgotten.

Let us consider an example. The group of symmetries of the snowflake in the picture below consists of six rotations by multiples of \pi/3, and six reflections (about three axes passing through the six arms of the star and three axes passing midway between these arms). This group is the same as the group of symmetries of the regular hexagon. In other words, we can identify the symmetries of the snowflake with the symmetries of a regular hexagon in a manner that preserves their composition operations. From the point of view of symmetry, the regular hexagon and the snowflake are the same.

The first chapter of Indra’s Pearls is titled The language of symmetry. It introduces groups, first as collections of transformations, and then axiomatically. Computer programs for enumerating over elements of groups are explained, and the reader is invited to both implement, and play around with these programs.

Symmetry as the arbiter of geometry

In Klein’s vision, a geometry is nothing more than a pair (X,G), where X is a set, and G is a group of transformations of X, to be thought of as transformations preserving a certain geometric structure on X. For Euclidean geometry, the space X is the two-dimensional plane, and the group G consists of the set of rotations followed by translations.

For another example of a geometry, consider a sphere, such as the surface of the earth. The lines of this geometry are the great circles (the shortest path along the surface of the earth between two points on it is a great circle). For this geometry, X is the set of points of the sphere and the group G consists of all rotations (about any axis) of the sphere.

An analogous description of the Poincaré disc is more subtle and involves Möbius maps.

Möbius maps and symmetries of the Poincaré disc

One of Klein’s revolutionary ideas was that any group of transformations can be used to create symmetry. While Euclidean geometry uses symmetries that are rigid motions, symmetry can also be created from maps which distort, stretch and twist. The group of Möbius maps is another group of symmetries of a sphere. Identify the points of the sphere (except for the north pole) with the points z in the complex plane via stereographic projection (see Figure 2). Identify the north pole with z=\infty. This avatar of the sphere, which allows for the use of methods from the theory of functions of a complex variable, is called the Riemann sphere.

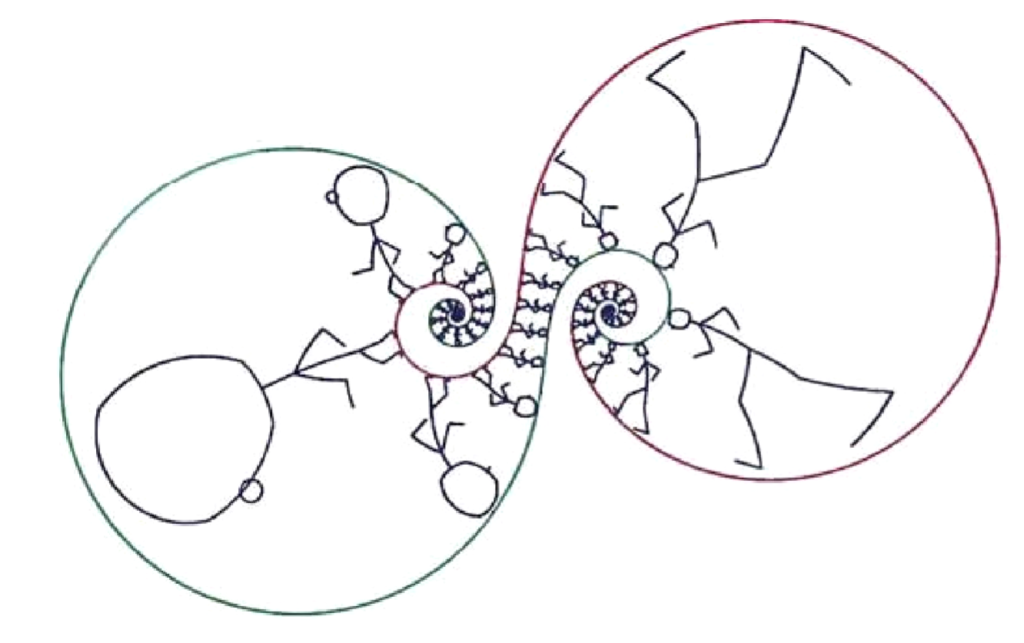
Möbius maps are transformations of the form z\mapsto \frac{az+b}{cz+d}, where a,b,c,d are complex numbers. Chapter 3 of the book is a detailed exploration of Möbius maps. They come in three flavours, parabolic, loxodromic, and elliptic. As a prelude to what comes in the rest of the book, the authors analyze the dynamics of Möbius maps – what happens when these transformations are applied repeatedly to the Riemann sphere. Figure 3 shows how Dr. Stickler is distorted by repeated application of a loxodromic Möbius map.

While the Möbius maps distort our (Euclidean) view of the world, they happen to be the right transformations for hyperbolic geometry. Consider the set of all Mobius maps that take the interior of the unit disc in the complex plane onto itself. These are the transformations z\mapsto \frac{az+b}{\bar b z +\bar a}, where |a|^2-|b|^2=1. Not only do they map the Poincaré disc onto itself, they also map “lines” of the Poincaré disc (circular arcs that meet the circumference at right angles and diameters of the disc) onto “lines”.

Pairing discs

The book takes off in Chapter 4, The Schottky dance. Given a pair of disjoint discs in the Riemann sphere, there is a unique Möbius map that maps the outside of the first disc into the inside of the second, and the inside of the second into the outside of the first. This Möbius map is thus said to pair the given discs. Now the main game of the book begins. Consider two pairs of discs, and the corresponding Möbius maps that pair them; call them A and B. We also take the inverses of these transformations, which we call a and b respectively. Consider the set \Gamma of transformations that are obtained by applying a sequence of transformations drawn from \{A, B, a, b\}. When the discs do not touch, \Gamma forms a group known as a Schottky group, named after a German mathematician Friedrich Schottky. This is a concrete realization of a free group on two generators. Each element of this group may be thought of as a word made from the four-letter alphabet \{A, B, a, b\}. Starting with different placements of the four circles and computer algorithms, one can plot the images of the original paired discs under the transformations in the Schottky group. As the words get longer and longer, the images of these discs shrink to give rise to fractal dust, which is the subject of Chapter 5, Fractal dust and infinite words. This fractal dust is called the limit set of \Gamma, which is the image of the original pairs of discs under infinite words. This set has very interesting analytical properties, much like the Cantor set. It displays self-similarities at all scales; no matter how much you zoom into them, you will find the same structures repeated at smaller and smaller distance scales. This set may turn out to be neither one-dimensional nor two-dimensional but instead, it may have a fractional dimension, hence the name fractal. Given the right choices of paired discs, these sets can be visually spectacular. Images of fractals entered popular culture after they were popularized by Benoit Mandelbrot’s book [1].

Geometry as local structure

Another modern view of a geometric structure is to impose on a set the notions of distance and angle in such a way that looking out into the space (the set under consideration) from any point in the space in any direction for a short distance, would be exactly the same as looking from any other point and in any direction for a similar short distance. This is clearly true in the Euclidean plane, because its group of symmetries (consisting of rotations followed by translations) can be used to move from any direction based at one point to any other direction based at any other point. Although it seems counter-intuitive, it is possible to put a geometrical structure on a torus (the surface of a doughnut or a tennikoit ring) in such a way that a small neighbourhood of any point looks exactly like a point on the Euclidean plane. One way to see this is to construct the torus from a flat rectangle by identifying opposite edges. This glueing process is beautifully illustrated by the first of Larry Gonick’s cartoons as displayed in Figure 4. This construction allows us to identify each point in the torus with a point in each tile of a tiling of the Euclidean plane by rectangles as in Figure 5, with opposite sides of each tile identified. Consider the group \Gamma of symmetries of the Euclidean plane consisting of left or right translations by a multiple of the length of the tile, upward or downward translations by a multiple of its breadth, and their compositions. Each transformation in \Gamma is also an element of the group of all symmetries of the Euclidean plane. When these symmetries are applied to a single point in the plane, it gives rise to one point in each tile. This collection of points is known as an orbit of the group of symmetries. The torus may be regarded as the space of \Gamma-orbits in the Euclidean plane. A small neighbourhood around each point on the torus looks just like a neighbourhood of a point in the Euclidean plane.

On short distance scales (much less than the length a or the breadth b) of such small neighbourhoods, notions of distance and angles can be transported to the torus. Patches of these geometric neighbourhoods glue together to give a geometric structure on the torus that is indistinguishable from the flat geometry of the Euclidean plane.

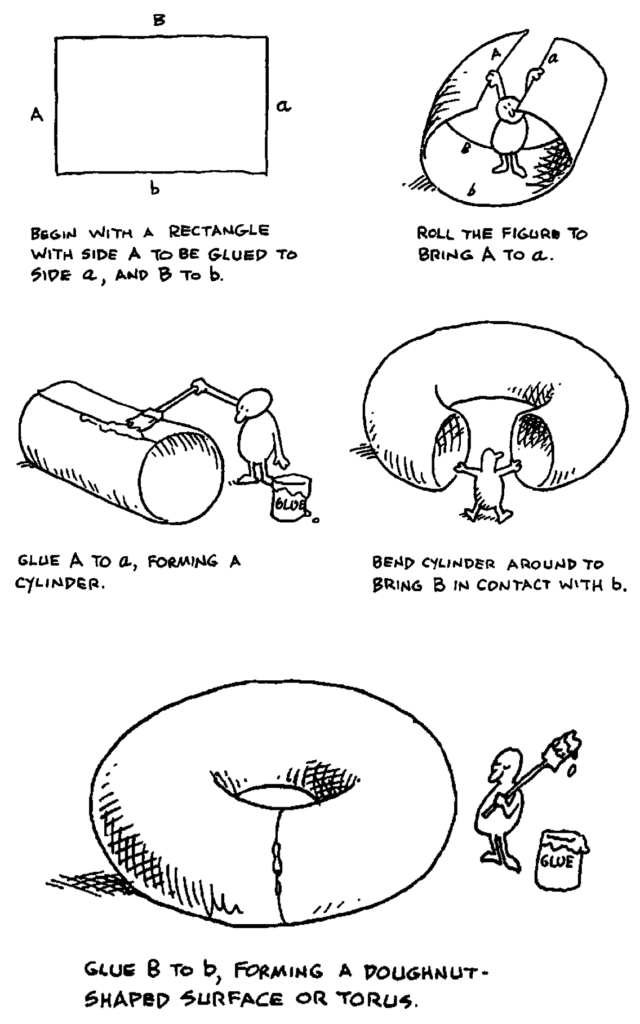
Given a Schottky group \Gamma, the complement of the set of fractal dust is called the regular set of the group \Gamma. It contains the complement of the two pairs of discs in the Riemann sphere. This complement may be viewed as a “tile” which is really a sphere with four discs cut out of it. Another of Larry Gonick’s cartoons is used to show how glueing along these cut-out-discs leads to the construction of a two-holed torus. This torus can be viewed as a space of orbits of the regular set for the action of the Schottky group \Gamma.

The uniformization theorem

The famous uniformization theorem for surfaces says that all geometries on surfaces come from three fundamental ones, namely the flat geometry on the Euclidean plane, spherical geometry on the sphere and hyperbolic geometry (the geometry of the Poincaré disc, where the parallel postulate fails for a different reason than in spherical geometry). An example of a surface is a “g-holed torus” (also known as a surface of genus g).

A 3-holed torus is shown in Figure 6. Innovative German bakers bake pastries called pretzels whose surface has genus 3. In the late nineteenth century, Poincaré and Klein proved that surfaces with genus more than one all come from tilings of the Poincaré disc, just as the torus comes from a rectangular tiling of the Euclidean plane.

Figure 7 shows a tiling of the Poincaré disc by heptagons. Although the heptagons in the tiling look different from each other, getting smaller and smaller as they approach the circumference of the circle, they are congruent in hyperbolic geometry. Each heptagon can be obtained from the central one by means of a symmetry of the Poincaré disc.

Just as a torus can be obtained from the plane as orbits of a group of symmetries where each orbit corresponds to a point in a rectangular tile, the 3-holed torus of Figure 6 can be obtained from the Poincaré disc as orbits of a group of symmetries, where each orbit corresponds to a point in a heptagonal tile. The groups of symmetries involved here are much more subtle.

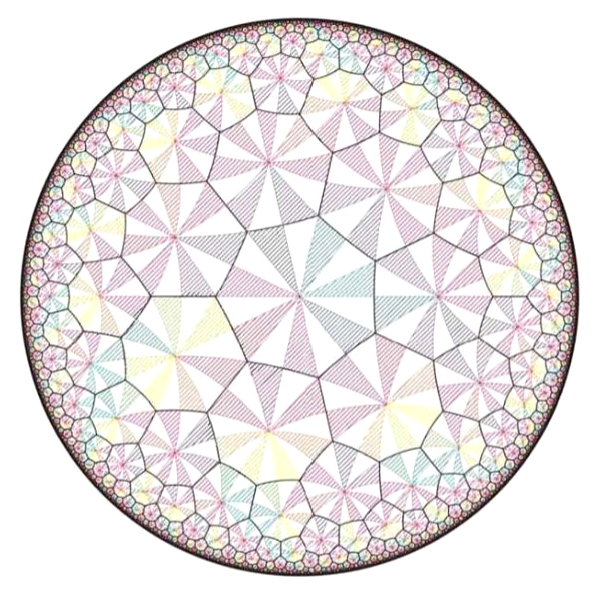
Poincaré and Klein showed that any surface with genus more than one can be realized as the space of orbits of some group \Gamma of symmetries of the Poincaré disc. A group \Gamma of symmetries of the Poincaré disc that gives rise to such a compact surface is known as a Fuchsian group.

To summarize, there are three fundamental geometries for surfaces. Following Klein’s vision, each can be characterized purely as a set, together with a prescribed group of symmetries. These are:

1. The sphere, whose symmetries are obtained by its rotations in 3-dimensional space.
2. The Euclidean plane, whose symmetries consist of translations followed by rotations in the plane.
3. The Poincaré disc (hyperbolic space), which is, as a set the unit disc in the complex plane. Its symmetries consist of Möbius maps of the Riemann sphere that map the unit disc bijectively onto itself.

The uniformization theorem states that every geometrical structure on a surface comes from a pair (X,\Gamma), where X is one of these fundamental geometries, and \Gamma is a discrete subgroup of the group of symmetries of X.

All the really interesting examples of (X,\Gamma) come from the Poincaré disc. The groups \Gamma involved are Fuchsian groups. They can be characterized as groups whose limit sets are contained in the unit circle. These are a very special subclass of a larger class of subgroups of the Riemann sphere called Kleinian groups, which play an important role in understanding three-dimensional analogues of hyperbolic surfaces.

The geometry of three-manifolds

Three-dimensional analogues of surfaces are called three-dimensional manifolds, or for short, 3-manifolds. Of 3-manifolds, William Thurston [6] said

One of the “recent” developments that Thurston was alluding to was his hyperbolization theorem, where he had shown that a very large class of 3-manifolds could be obtained from three-dimensional hyperbolic space in much the same way as every surface of genus two or more could be obtained from the Poincaré disc.

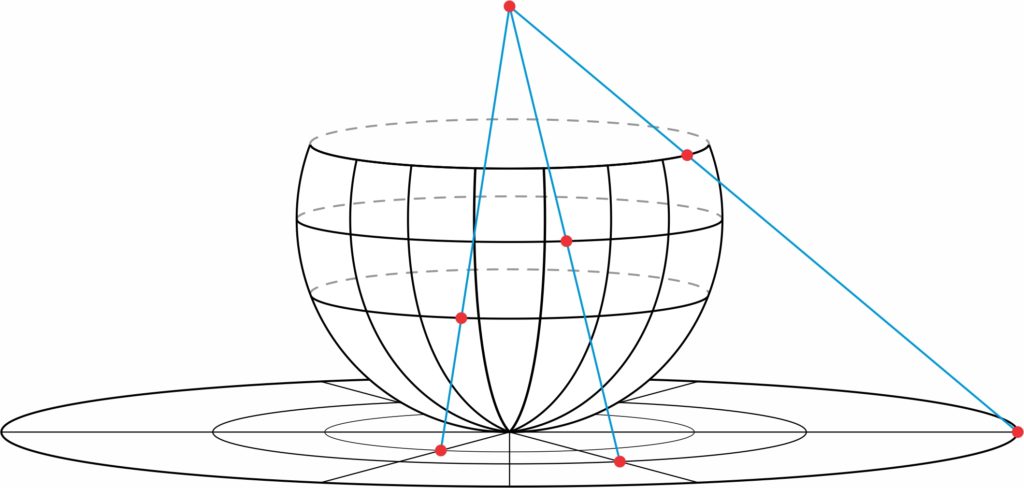
Just as two-dimensional hyperbolic space is modelled on the unit disc, three-dimensional hyperbolic space is modelled by the unit ball in three-dimensional space. Lines in this space, the “Poincaré ball”, consist of semicircles that are perpendicular to the boundary sphere and diameters of great circles [in the boundary sphere]. Planes are spherical bubbles that meet the boundary sphere at a right angle, or planes that contain great circles [of the boundary sphere]. The boundary of the Poincaré ball can be regarded as the Riemann sphere. Poincaré observed that every Möbius map of the Riemann sphere extends to a transformation of the whole ball, and these extensions are the symmetries of three-dimensional hyperbolic space. All 3-manifolds with hyperbolic geometry arise as spaces of orbits of this Poincaré ball by Kleinian groups. Thus, Kleinian groups play an important role in understanding 3-manifolds with hyperbolic geometry.

In his 1982 paper [6], Thurston conjectured that every compact 3-manifold can be cut up into pieces such that every point in each piece comes from one of eight fundamental geometries, the most common being three-dimensional hyperbolic space. This famous geometrization conjecture included as a special case a notorious conjecture going back to Poincaré, which says that every compact 3-manifold where every closed curve can be continuously deformed to a point, is topologically the same as the 3-dimensional sphere (the unit sphere in four-dimensional space).

The greatest achievement of low-dimensional geometry was perhaps the proof of Thurston’s geometrization conjecture by Grigori Perelman, who announced the proof in 2003, a year after the publication of Indra’s pearls. In 1982, Richard Hamilton had proposed an evolution process on the notions of distances and angles on a manifold. Perelman proved the geometrization conjecture by generalizing and refining Hamilton’s ideas. For a survey of the Poincaré and geometrization conjectures, see [2].

The rich world of limit sets of Schottky groups

Chapter 6 of the book, titled Indra’s necklace introduces quasi-Fuchsian and Fuchsian groups. This is also the chapter where the true beauty of limit sets begins to develop.

By carefully making the two pairs of circles touch, and a careful choice of generators of the Schottky group, it is possible to construct kissing Schottky groups. The limit set of such groups coalesces to lie inside a connected curve (albeit still exhibiting intricate self-similar kinking patterns) that divides the Riemann sphere into two connected components. Either the limit set can be all of such a curve, or it can consist of fractal dust inside such a curve. The associated groups are called quasi-Fuchsian groups. When the limit set is contained in a circle, the group is called a Fuchsian group, and is involved in the construction of hyperbolic surfaces as described in an earlier Section.

Chapter 7 illustrates another amazing kind of limit set, the Apollonian gasket. This set can be constructed using an iterative process that begins with three mutually tangent circles (for example, three of the four largest circles inside the outer circle of Figure 8). There is a triangular region (bounded by arcs) between these circles. Draw the largest inscribed circle inside this triangular region. Now the new circle is tangent to each of the three earlier circles, and with every pair of them, encloses a triangular region. Inside each of these regions, draw another largest inscribed circle. Each time a new circle is drawn, it bounds three new triangular regions.

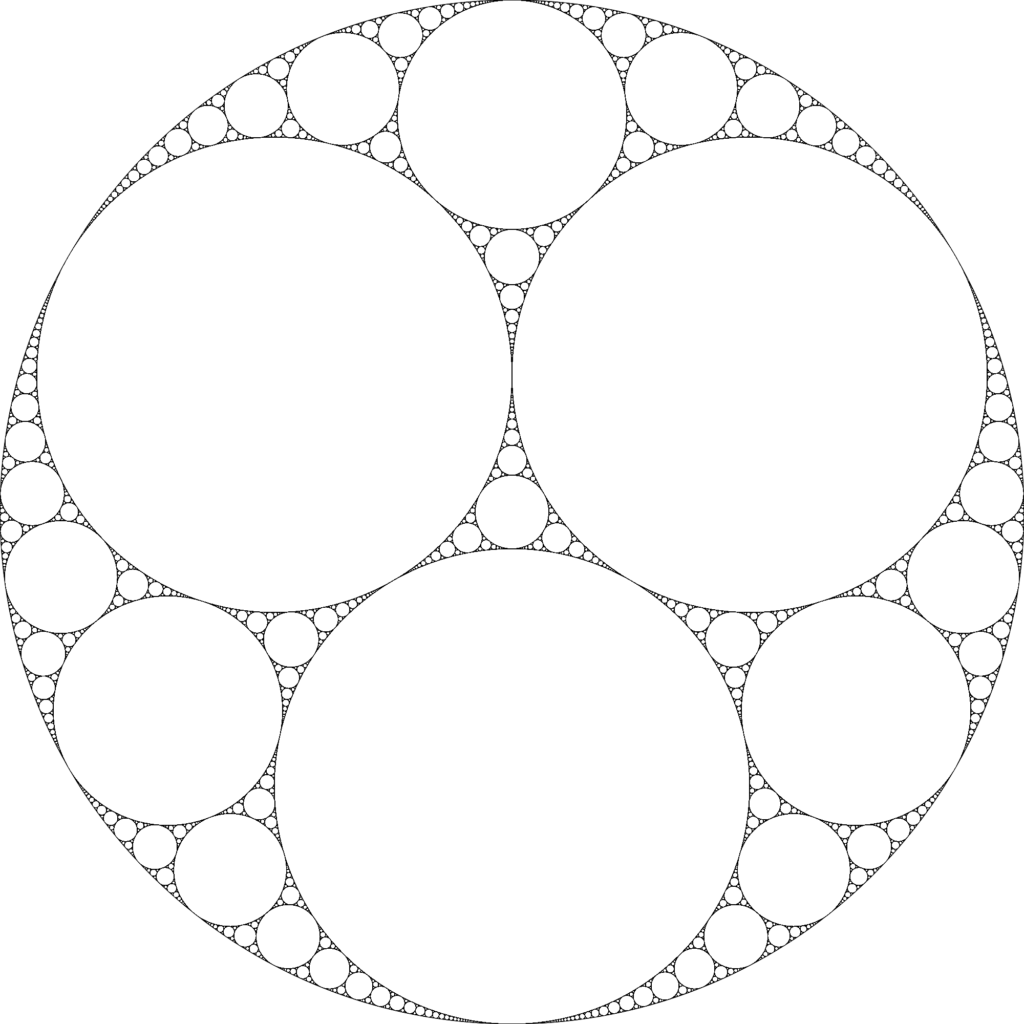
These are to be filled with their largest inscribed circles in the next step. Working on the Riemann sphere by adding a point at infinity to the plane, the region outside the three original circles can also be regarded as a triangular region containing \infty.

Performing this iterative process infinitely results in Figure 8 (which also appears on p. 197 of the book). What is amazing is that this set is the limit set of a Schottky group. Even more amazing is the discovery, inside this Schottky group, of the famous modular group that comes from Möbius maps with integer parameters, whose study goes back to Klein and Fricke.

In Chapter 8, the authors do away with Schottky discs and consider general pairs of Möbius maps. Using symmetry considerations, they reduce the number of parameters involved in the choice of these maps from eight to three. This allows for a game with different rules, leading to new behaviour of limit sets. The book progresses through the remaining chapters, playing with such groups and exploring the images that are generated, which are often stunning, and sometimes chaotic. The discussion gets more intricate and the mathematical implications more subtle. The book ends with an epilogue that explains the motivation for many of its explorations.

A book that can be read at many levels

Indra’s Pearls is a book that can be read at many levels. The early chapters should be accessible to anyone with an interest in mathematics and a college-level background. To participate in the mathematical experiments requires a more serious commitment. A committed student of mathematics who is curious to learn more about geometry would benefit the most. Indra’s Pearls is also a work of art that is grounded in mathematics. The metaphor of Indra’s Pearls is taken from the Flower Garland Scripture, a text of East Asian Buddhism. Each of the pearls in Indra’s net of pearls reflects all the others. In effect, the entire Universe is reflected in each pearl. \blacksquare

1. B. Mandelbrot, The Fractal Geometry of Nature. W.H. Freeman and Company, 1982.
2. J. W. Morgan, Recent progress on the Poincaré conjecture and the classification of 3-manifolds. Bull. Am. Math. Soc., 42:57–78, 2004.
3. G. Perelman, The entropy formula for Ricci flow and its geometric applications. arXiv:math/0211159, 2002.
4. G. Perelman, Ricci flow with surgery on 3-manifolds. arXiv:math/0303109, 2003.
5. G. Perelman, Finite extinction time for the solutions to the Ricci flow on certain three-manifolds. arXiv:math/0307245, 2003.
6. W. Thurston, Three-dimensional manifolds, Kleinian groups and hyperbolic geometry. Bull. Am. Math. Soc., 6:357–381, 1982.

Footnotes

1. Taking inverse is the mathematical term for `undoing’ an operation. ↩