
Vaughan Jones is best known for his work on von Neumann algebras, knot theory and conformal field theory. One of his most famous discoveries is a polynomial, which now bears his name, and resolved many long unsolved problems in knot theory. Diligent and persisting in his approach to research, pleasant in disposition, caring and generous with colleagues and students, serious in the pursuit of several of his interests like music, kitesurfing, travelling, and happily adventurous in spirit, his sudden and unexpected recent passing away robs the world of mathematics of an exciting and decorated mathematician of our times, leaving a void deeply felt in the lives of his colleagues, family and friends.
David Evans and Sorin Popa1
Sir Vaughan Jones died aged 67 on September 6th 2020, following complications owing to a severe ear infection. An inspired and inspiring mathematician of exceptional originality and breadth, his enduring work brought together several disparate areas of mathematics, from analysis of operator algebras to low dimensional topology, statistical mechanics and quantum field theory, with major impact and unexpected and stunning applications even outside of mathematics, as in the study of DNA strands and protein folding in biology. A crucial idea leading to these striking connections was his groundbreaking discovery in the early 1980s that the symmetries of a factor (an irreducible weak^{*} closed algebra of operators on Hilbert space), as encoded by its subfactors, are quantized and generate quantized groups, which is itself a completely new type of structure endowed with a dimension function given by a trace and an index that can even be non-integral.
Vaughan Jones was born on December 31st 1952, in Gisborne, New Zealand. He was educated at Auckland Grammar School and the University of Auckland, where he earned a Bachelor of Science and a Master of Science with first class honors. He then received a Swiss government scholarship and completed his PhD at the University of Geneva in 1979, under the supervision of André Haefliger and Alain Connes, with his thesis awarded the Vacheron Constantin Prize. He was a Hedrick Assistant Professor at the University of California at Los Angeles (UCLA) in 1980-1981, and worked at the University of Pennsylvania between 1981-1985, before being appointed a full Professor at the University of California, Berkeley in 1985. From 2011 onwards, he held the Stevenson Distinguished Chair at Vanderbilt University, while also being Professor Emeritus at UC Berkeley.
Already in his thesis, Vaughan Jones was interested in the classification of finite groups of automorphisms (“classical symmetries”) of a class of von Neumann algebras called II_1 factors, following up on Connes’ classification of single automorphisms. He developed a novel, algebraic approach, where the action of the group was encoded in the isomorphism class of a subfactor. Soon after, this led him to consider abstract subfactors together with a natural notion of relative dimension, that he called index, and to study the values it can take. By late 1982, he made a series of amazing discoveries. On the one hand, the index of a subfactor can only take values in the discrete set \{4 \cos^2(\pi/n)\mid n\geq 3\} or in the continuous half-line [4, \infty). On the other hand, all these values can actually occur as indices of subfactors, and indeed, as indices of subfactors of the most important II_1 factor, the so-called hyperfinite II_1 factor (the non-commutative, quantized version of the unit interval). The proof involved the construction of an increasing sequence of factors (a tower), obtained by iteratively “adding” projections (i.e., idempotents) satisfying a set of axioms which together with the trace provide the restrictions. Shortly after, Jones realized that his sequences of projections give rise to a one-parameter family of representations of braid groups, and that appropriate re-normalizations of the trace give rise to a polynomial invariant for knots and links – the Jones polynomial.
This immediately led to a series of spectacular applications in knot theory, solving several of the so-called ‘Tait conjectures’ from the 19th century. More importantly, it completely reinvigorated low dimensional topology, igniting totally unexpected developments, with an exciting interplay of areas including physics, and engendering a multitude of new invariants for links and 3-dimensional manifolds, summarily leading to a new brand of topology, Quantum Topology.
This revolutionary work also had a huge and far-reaching impact in the theory of II_1 factors and operator algebras, posing exciting new questions about the classification of subfactors, and of the quantized groups they generate. Many outstanding results by a large number of people have since followed. Jones was deeply involved in this development, notably finding the best way to characterize the group-like object arising from the tower of factors (the standard invariant), as a two dimensional diagrammatic structure of tangles called planar algebra (1999), and then classifying them up to index 5 in a remarkable programme developed with some of his former students (2005-14). This, together with a quest to produce conformal field theory from subfactors, led Jones to a study of the Thompson groups and again to unexpected spin-offs for the theory of knots and links (2015-2020). In a parallel development which started in 1983, a connection was established with calculations by Neville Temperley and Elliott Lieb in solvable statistical mechanics, triggering yet another series of connections with statistical mechanics, and conformal quantum field theory, where a similar dichotomy is observed between the discrete and continuous parts of the central charge.
By late 1982, he made a series of amazing discoveries.
Vaughan Jones was awarded the Fields Medal in Kyoto in 1990, and was elected Fellow of the Royal Society in the same year, Honorary Fellow of the Royal Society of New Zealand in 1991, member of the American Academy of Arts and Sciences in 1993, and of the US National Academy of Sciences in 1999. In addition, he was a foreign member of the national learned academies of Australia, Denmark, Norway and Wales. He received the Onsager Medal in 2000 from the Norwegian University of Science and Technology. In 2002, he was made a Distinguished Companion of the New Zealand Order of Merit, and later re-designated Knight Companion. The Jones Medal of the Royal Society of New Zealand is named in his honour.
He had a strong commitment of service to the community. In 1994, he was the principal founder and Director of the New Zealand Mathematical Research Institute, leading its summer schools and workshops every January. He was the Vice President of the American Mathematical Society between 2004-2006, and also the Vice President of the International Mathematical Union between 2014-2018.

Vaughan had a very distinctive and personal style of research in mathematics. His warmth, generosity, sincerity, humour and humility led him to thrive on social interaction, and enabled the mathematical community to significantly benefit from his openness in sharing ideas through every stage of development, right from initial speculations and conjectures about the way forward, up to the discussion and explanation of the final results. His presence both at formal and informal events, and his regular interaction with mathematicians, especially graduate students including his own, and of which he had more than 30, enriched all who came into contact with him. Vaughan regularly mixed his passion for skiing and kitesurfing with hosting informal scientific meetings at Lake Tahoe, Maui and his family retreat in Bodega Bay. His love for rugby was legendary, as was the fact that he wore an All Blacks jersey for his plenary address at the International Congress of Mathematicians in Kyoto, following the award of his Fields Medal. His other major passion was music, choral singing and orchestral playing, shared intimately with his family and friends. Vaughan is survived by his wife Martha (Wendy), children Bethany, Ian and Alice and grandchildren. He will be dearly missed by his family and many friends all over the world.
Author bio: David Evans is an Honorary Distinguished Professor at Cardiff University, UK, and Sorin Popa is a Professor at the University of California Los Angeles, USA.
V.S. Sunder
Vaughan Frederick Randal Jones, an eminent von Neumann algebraist passed away on the night of September 6th 2020. Among the highlights of his work were the index of subfactors and a polynomial invariant of knots and links in \mathbb{R}^3. I am writing this short obituary note for Vaughan, in view of my personal and professional proximity with him.

Actually, on his first visit to India, he gave a series of perhaps around twenty lectures in Delhi, Chennai and Bangalore. I really wanted those lectures to be written up but did not think any graduate student would be up to the task, so I took it on myself; the result was our `co-authored’ book on Subfactors which was published2 as a London Mathematical Society book.
He had a fondness for India, particularly its food. During his first visit in 1994, for a few weeks he had not been eating any meat and mused on turning vegetarian, but this urge lasted less than a week of his return to hamburger country!
He had a fondness for India, particularly its food
Vaughan has come to India on several occasions, and once came around my 60th birthday when I was supposed to retire. Basically, he was supposed to be here, along with his wife Wendy, to mark that occasion, but it turned out that his daughter was going to deliver a grandchild just around that time, and so they had to go back to welcome their grandchild. Wendy returned to the US a little earlier than Vaughan. I remembered a saying about a baby being born with a silver spoon in her mouth, and so I went and got a tiny silver spoon that Vaughan could take back…
I should also briefly describe how our research students were influenced by each other. Thus Vaughan was very interested in a construction of one of my first PhD students, Uma Krishnan, which involved what he called bipermutations, and the outcome was that his student Bina Bhattacharyya wrote a thesis on Krishnan-Sunder subfactors. On hearing about this, Uma said in a very forlorn tone that Krishnan had no clue on these or any subfactors!

Another student of Vaughan at about the same time was Zeph Landau, who is quite a close friend now. We have visited one another in Berkeley, New York and Chennai for varying periods; and there are some papers we co-authored, some with Vijay Kodiyalam. Another student of mine who wrote his thesis around that time was Shamindra Ghosh. When Vaughan saw Shamindra’s thesis, he said he would have been proud if one of his students had written it!
Author bio: V.S. Sunder is a Professor at the Institute of Mathematical Sciences in Chennai. His research interests center around Hilbert space and focused on operators, operator algebras, subfactors, planar algebras, and free probability.
The following interview article3 is based on an informal conversation of Jones with Aurélien Alvarez,4 the video clippings of which are at https://images.math.cnrs.fr/Des-tresses-au-kitesurf-Vaughan-Jones.html. Supplemental notes between the videos are added with the hope that the readers will also enjoy reading about this mathematician-surfer Vaughan Jones looking back at some of the highlights of his career.
Supplemental notes:
It has been a tradition for ten years now, that the students of the mathematics department of the École Normale Supérieure de Lyon are invited to spend a mathematical weekend at the Château de Goutelas in the company of a renowned mathematician talking about some of the discoveries or mathematics. In the year 2012, it was Vaughan Jones.
One of the astonishing points of this story is how Vaughan Jones got his hands on his polynomial in a totally unexpected way since he was interested in completely different problems in functional analysis. No surprise then that he was awarded the prestigious Fields Medal in 1990.

Initiation
AA: How did you get into maths, Vaughan?5 Did it start from your very early days
VJ: A hundred plus a hundred was two hundred. They were gigantic numbers! I knew one plus one was two, so I deduced that a hundred plus a hundred must be two hundred. Great! I was the only one in the class to have had such thoughts. I was good at maths, and as it got stronger, I got even more and more interested in maths. There was constant reinforcement. I have to say that it was both maths and physics equally. It was always maths and physics, and it was only at the thesis level that I really chose. Besides, I started in physics: the beginning of my thesis was in theoretical physics in Geneva, at the school of physics.
AA: On what topic

VJ: It was the mathematical foundations of quantum mechanics, and so it was still a bit of a cross between maths and physics.
AA: Is that what led you to operator algebras
VJ: Yes, absolutely. I studied in New Zealand until I was twenty-one, and I left New Zealand because I got a scholarship from the Swiss Confederation to go to Geneva to continue my studies with Professor Jauch, who was a specialist in the mathematical foundations of quantum mechanics. I knew a little about von Neumann algebras. I had already learned them in New Zealand. I had a teacher who had shown me a bit of von Neumann algebras.
So when I arrived in Geneva, I first had language lessons to learn French. The language courses were in Fribourg and I spent three months there before going to Geneva. It was very nice, and really good, the coolest three months of my life, I think. It was French lessons in the bistro6; we went for walks in the mountains and all that, which was really nice during these three months. Then I said to myself, well, I have to go now to Geneva to meet Professor Jauch, and went there. I took the train, went to the Institute of Theoretical Physics, and saw him. He was very nice: “Yes, we are happy that you have come”, etc. and then I returned to Fribourg for the language courses. A week later, I heard the sad news: Jauch was dead!
AA: Oh!
VJ: I was invited to the funeral. Maybe that’s perhaps when I finally changed to maths altogether. In Jauch’s group, there was a person called Constantin Piron, who guided me along a bit. He was very good, but somehow I wasn’t very happy with the job I was doing. It seemed to me that it was really straddling both physics and maths, and maybe it didn’t feel very deep to me, at least whatever I was doing then. At the same time, I was also taking a course with André Haefliger,7 in the maths section, across the road. I asked him at one point if he needed an assistant and he said, “Yes, you can start tomorrow, I have my assistant leaving.” So I changed and since then, I would say, I have been much more of a mathematician than a physicist – without however completely forgetting what I had learned in physics.
A look back at the highlights of Vaughan’s career.
AA: What are the highlights of your career
VJ: That’s interesting, the highlights of my career in maths! There was this first highlight, which is when I asked Haefliger [laughs] that I wished to change to maths; that was a very decisive moment. Unfortunately, I broke my leg right after, on skis! I was very scared because I said to myself, `I can’t do my job as an assistant! They’re going to fire me’ and all that…. So I came to the institute on crutches like this [mimics the movement].

AA: Was that during your thesis
VJ: It was during my thesis. Connes spoke for three hours, nonstop. I was amazed! I knew a little bit about what he had done in von Neumann algebras and that was when he started to put out his stuff on foliations. Because of my stint with Haefliger, I already knew foliations pretty well, and Connes’s talk made the connection between the two ideas very strong for me. So there it was …, it was really great!
The third highlight, I think, was when I obtained the key idea that I needed so as to finish my thesis. My thesis was on the actions of groups on a certain von Neumann algebra – a hyperfinite factor of type II_1 – and there was a problem. Alain Connes had done it in the case of cyclic groups and I was able to extend that idea without too much difficulty, to the case of an Abelian group. It’s not that obvious, but I succeeded. However, in the noncommutative case there was a pretty big problem. So, I quite distinctly remember the precise moment when I hit upon the idea. In Switzerland, they have this Fasnacht9 – the city has a party night. I had a friend in Zurich, and I went there for Fasnacht, and I ended up drinking a lot – I was young after all. The next morning, I was really… sick as anything could be, but it was also at that very moment that I had the essential idea to finish my thesis; and back during the train journey from Zurich to Geneva, I developed it further. After that key moment, it was just a matter of routine to get the thesis.
AA: Were there other highlights
VJ: There were several other highlights too. There was this question about the possible values of the index of a factor. I had my first result in this area, and while it was not a very strong moment, it was also not that bad either. There was also a gap in the index, that the index could not be between 1 and 2, and 2 was isolated. Therefore, I was happy and I wanted to publish it. Once again, it was Alain Connes who gave me some very, very good advice. He said, “No, no! You will solve the problem. What are the values of the index?” He asked. Then I worked, I worked, and I worked some more, and it was really very, very hard because there simply wasn’t any structure; we just did not know what to do. Finally, I got it by iterating the proof that there was no value between 1 and 2. Little by little, the ideas came in, and I remember a series of really strong moments, when I found a gap between 2 and the next value, and then finally there was a series of values tending towards 4. There was this diagram that I had seen in the course, a kind of a truncated Pascal triangle; and other truncated diagrams for some more special values. That moment, and its aftermath lasted very strongly for at least a year! I had a lot of adrenaline in my brain, I think….

Another highlight was in Geneva where I gave a long lecture. I wrote down my algebraic relations – now called Temperley-Lieb relations – and there was someone in the room, a study buddy by name Didier Aternole, who said: “Ah! but it looks like a braid group!” Surely, there were other people who noticed it and who could have explained it to me, but it was Didier who first explained the braids to me. He explained the drawings to me, \sigma_1 \sigma_2 \sigma_1 etc. and I said: “Hey, hey, it’s funny!” Then I found the representations of the braid groups, the ones that I had explained lengthwise and crosswise. I found them that very day, doing a little computation. For me, it was a highpoint but when I tried to sell them, no one was interested in it. I find it quite remarkable in the history of maths, that at that time there was no interest in linear representations of braid groups. Ten years later, everyone was studying linear representations of braid groups.
 |
 |
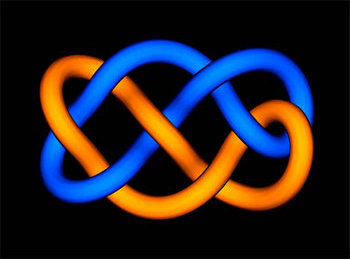 |
Supplemental notes:
Factors are the “building blocks” in the theory of von Neumann algebras, in the sense that it is “enough” to study the factors to understand von Neumann algebras well. Factors were classified into three main families by the foundational work of Francis Murray and John von Neumann at the turn of the 1940s, i.e., classification into types I, II and III. What Vaughan Jones studied in the early 1980s was the value of the index. The index is a positive real number that “measures the relationship” between a factor of type II_1 and a sub-factor thereof.10
As Vaughan says in the video extract, before arriving at 4 and to be able to take all the possible real values, the index starts from 1 and goes towards 4 by making jumps: 1, then 2, then \frac{(3 + \sqrt{5})}{2} = 2.618, …, then 3 then 3.247 etc.
 |
 |
The next highlight was right after the discussion with Joan Birman,13 in the particular moment when I thought to myself: Why don’t you simply take the trace of the braid, instead of doing complicated stuff …? And it worked! So that was a really strong moment once again, and there was again an euphoria that lasted for quite a while, while I was doing the initial calculations. I calculated a lot of Jones polynomials those days. I even wrote a computer program in Pascal, which was also the first program to ever do it.
Supplemental notes:
In the article by Luis Paris14 (from which the images above are taken), Vaughan’s work on knots is quickly covered. One of the fundamental questions of the theory is: given two knots, are they the same and how do you tell them apart?
Even if one has to mathematically define what a “knot” is, and what one means by “are the same”, we all have a good intuition about that: a knot is one that can be made with a piece of string (one has to take care that the string must not have free ends), and two knots are the same if, by manipulating our strings without cutting them, we finally succeed in convincing ourselves that they are indeed the same! A link is simply several knots entangled with each other.
The Jones polynomial is what mathematicians call an algebraic invariant. What they mean is that each time they are given a knot (or more generally a link),15 they are able to associate an algebraic quantity (here a polynomial) which is the same for two (oriented) links which are the same. The Jones polynomial is a Laurent polynomial, denoted by V, in the variable \sqrt{t}: concretely, it is a polynomial with powers of \sqrt{t} and (\sqrt{t})^{-1}. Here are some examples:
One of the great strengths of the Jones polynomial is its ability to distinguish certain links from their mirror images. But the Jones polynomial is far from revealing all of its secrets. Here is an open and a very natural question:
Apart from the trivial knot, are there knots whose Jones polynomial is 1?
For links (with at least two components), the answer is known,16 the simplest counterexample being this link17:
More recent work: Planar algebras
VJ: There was a very strong moment quite recently when I discovered the work with Dima Shlyakhtenko18 and Alice Guionnet,19 when I saw that we could use planar algebras and a construction of graded rings to construct factors and sub-factors.
Then I restricted myself a bit. When I was younger I used to think that I was working in “maths in general”, but now I’m a little too small for “general maths” so I am specialising, especially in the plane, because from all these results with factors, sub-factors, braids, statistical mechanics and conformal field theory, I finally saw that all these play out in a planar world. I invented these planar algebras to try to understand this work with all these quite diverse objects. It must be said right away that I am not the only one to have had this idea. There are different versions available, and I like mine. I find that it has advantages. So there is this story of planar algebras that turns out to be so rich that I spend practically all my time finding interesting stuff in planar algebras.
 |
 |
One reason for the richness of planar algebras is the following: we know that there is the four-colour theorem.20 We know that any planar map can be coloured with four colours, and we know that if we start drawing maps on surfaces of higher genus, perhaps more colours are needed, but the result is easier to prove. So it is the case of the plane which is the most difficult. We worked for a very long time to solve it and finally, we still need a computer to prove it. I would like to have a little structural proof, in planar algebras.
AA: Oh yes!
VJ: But I couldn’t do it. Finally, I changed my point of view a bit because recently, I started to understand the proofs that exist for the four-colour theorem. I see here that there is a machine that produces a bunch of cases, and you have to produce a list of cases that you can deal with, by now revising it using combinatorial methods. Here, I realized that there are hundreds of thousands of cases that you have to produce. I also saw that in each of these hundreds of thousands of cases, there is one family of planar algebras. It’s quite astonishing, and this is why the sub-factors, and all that structure, are so rich. We will surely not be able to understand everything, at least not in this century….

AA: Even in this century which is in its early years
VJ: Yes!
And the waves in all of this?
AA: And the waves in all of this
VJ: Yes, I was thinking about waves for completely unrelated reasons, because I liked windsurfing. Now it has become kitesurfing, my favourite sport. There are quite a few extremely interesting problems here. For example, if you are on the water and there is a cliff; if you get too close to the cliff, especially if the wind is a sea breeze and blowing towards the cliff, and also if you are approaching the cliff, with only a moment to spare, you must absolutely avoid these cliffs. I have had adventures because of that. So I thought to myself: `Until what distance do the cliffs disturb the wind when the wind blows against the cliff?’ This kind of problem has anyway been solved by experts.
Then there is a question that I asked myself, for which I did not get a satisfactory answer, and it is this. When there is a sufficiently strong wind, there are these white horses,21 right? So you take the situation where you have land away so far, and the water starts there [points with his hands], and there’s a strong land breeze blowing like that. For a while, on the water, there are no white horses and after a certain distance, white horses commence. So the distance to the first white horse depends first of all on the force of the wind, and then on the shape of what is below the water…..
AA: Of the seabed.
VJ: There you go. So the question is: first, if we give ourselves a shape of the seabed which is simply flat, like a dug hole, what is the distance to the first white horse according to the wind speed? Well, I didn’t get an answer. That’s a very well posed question, eh? In a sense, it’s for these kinds of stuff that I have looked at partial differential equations.
AA: Okay. And do you think knowing a bit of knot theory is a big advantage for kitesurfing
VJ: You will see Monday evening, if you come to my lecture, that anyone who kitesurfs is already an expert in entanglements or links and braids. Every time you rig a kitesurf, in fact, you solve a problem that we saw in my course, which is how to transform an entanglement into a braid and then, how to make a braid into an identity, that is to say, the existence of inverses in the braid group.
AA: Okay.
VJ: We go through this: everyone who kitesurfs, every time they kitesurf, they do this, although I might be the only one who knows – not the one who knows how to just kitesurf, but who knows what he is doing from a mathematical point of view. It doesn’t help, but it’s nice… I said to myself: `Oh yes! I make a braid, I reduce this braid to the trivial braid… And it is very important that the braid is trivial because otherwise, you can die… [laughs].
AA: Oh yes!
Post Scriptum
These comments were collected with the help of Damien Gaboriau at the Château de Goutelas on March 4, 2012. The images of the oriented links accompanied by their Jones polynomials come from the article The Jones Polynomial22 by Vaughan himself. \blacksquare
Footnotes
- This article originally appeared in the bimonthly email newsletter IMU-Net of the International Mathematical Union in its September 2020 edition, and is republished here, with minor edits, with permission of both the authors and IMU-Net. ↩
- Introduction to Subfactors, V. Jones and V.S. Sunder. London Mathematical Society, Lecture Notes Series 234, Cambridge University Press. 1997. 162+ x ii pp. ISBN 0-521-58420-5, paperback. ↩
- Bhāvanā is grateful to Jérôme Germoni for help with transcribing from the video clippings. ↩
- Aurélien Alvarez (aurelien.alvarez@ens-lyon.fr) is a Professor at the École Normale Supérieure de Lyon. He is also the editor-in-chief of the online journal Images des mathématiques. ↩
- Contrary to appearances, this first name is pronounced “VON” and not “VOGAN”!. ↩
- a modest informal European-style restaurant or café. ↩
- André Haefliger is a Swiss mathematician, best known for his work in topology, knot theory and foliation theory. ↩
- Alain Connes is a French mathematician whose early work concerned the theory of von Neumann algebras. He was awarded the Fields Medal in 1982, in particular for his classification of type III factors. ↩
- Swiss carnival. ↩
- No need to try to understand precisely the meaning of the preceding words, it is quite obvious that what is said here is too little to understand anything. ↩
- Harold Coxeter was a British mathematician, one of the great geometers of the 20th century and an inspirer of the Dutch artist Escher. ↩
- https://en.wikipedia.org/wiki/Metaplectic_group. ↩
- Joan Birman is an American mathematician, and a great specialist in knot theory. ↩
- http://images.math.cnrs.fr/Les-tresses-de-la-topologie-a-la-cryptographie.html?lang=fr. ↩
- To be precise, the knot or link must be oriented: on each knot, put a small arrow indicating the direction that a small ant wishing to walk along the knot should follow. ↩
- Here are two references for the cognoscenti: Thistlethwaite, Links with trivial Jones polynomial, J. Knot Theory Ramifications (2001); Eliahou-Kauffman-Thistlethwaite, Infinite families of links with trivial Jones polynomial, Topology (2003). ↩
- This `link’ here is not any url link :-). ↩
- Dimitri Shlyakhtenko is an American-Russian mathematician who works at the University of Los Angeles, notably specialising in the theory of free probabilities. ↩
- Alice Guionnet is a French mathematician who works at the École Normale Supérieure de Lyon, in particular, a specialist in random matrices. ↩
- To know more about the four-colour theorem, see https://en.wikipedia.org/wiki/Four_color_theorem. ↩
- waves that are white at the top. ↩
- https://math.berkeley.edu/~vfr/jones.pdf. ↩
