The Elves of Mathematics

This article is based on `lectures’ in simple everyday language that I’ve been giving to mostly non-mathematical visitors on some motifs (as you’ll see in the photographs below) in our house. Hopefully, this written version shall appeal to a wider audience.¹

“Perfectly proportioned”

The defining property of a golden rectangle is that if we delete from it a square on a smaller side, then we are left with a similar rectangle, i.e., one having the same length-to-breadth ratio, and this ratio, that is, the common length-to-breadth ratio of all golden rectangles, is called the golden ratio.

The two murals near the front door depict golden rectangles. Thus, deleting the blues gives a smaller golden rectangle, then, by throwing away the bluish greens, another which is still smaller, and after three more deletions, one arrives finally in these murals at the tiny white rectangles. Indeed, the inherent limitations of masonry, or for that matter, any practical form of visual representation, clearly dictate that one would need to stop sooner or later, at some point or the other. However, what the spiralling in these murals is intended to evoke is that, in our God-given unlimited imagination, there is, just as clearly, no need to stop, now or ever. We can continue deleting a square on a smaller side for as long as we wish! And therein, in this evoked idea, as I’ll presently show, lies the real beauty of these depictions, a beauty which transcends by far their mere visuals, and in my humble, but admittedly prejudiced, mathematician’s opinion, is far more fetching than anything the best painter has ever painted, or the best poet has ever written.

In fact, these `mere visuals’ already have–-as you can confirm from an Internet search–-a huge fan following. From Phidias, through Leonardo da Vinci, to Le Corbusier, the architect who planned Chandigarh, the proportions of the golden rectangle have been raved about by all sorts of aesthetes, with Corbusier even opining that the navel divides a perfectly proportioned human body in the golden ratio, and then the two parts, in turn, are divided in the same ratio at the throat and the knees respectively! I’ve nothing to add to all this, but I do have something to say about an assertion that one finds on quite a few websites, and also on a panel in the City Museum in Sector 10, Chandigarh, namely that, “the golden ratio is equal to 1.618”. This is simply not true!

The golden ratio is not equal to 1.618 (recall that 1.618 is the decimal notation for 1618 by 1000). To see this, we note that, if the length-to-breadth ratio of our rectangle were 1618 by 1000, we could have subdivided each side of our rectangle into either 1618 or 1000 appropriately chosen equal units. Then, by drawing parallels through these subdivision points, we could have partitioned the rectangle into 1618 \times 1000 equal squares. The deletion of the blues would have entailed throwing away 1000 \times 1000 of these small squares, and then, that of the bluish greens, 618 \times 618 more of these small squares, etc. So, since we have finitely many small squares in all, and are throwing away some at each step, we would have been done (even in our imagination) in finitely many steps. This contradicts the fact that the deletion process can (in our imagination) continue for as long as we wish. So, the length-to-breadth ratio of our rectangle is not 1618 by 1000, i.e., the golden ratio is not equal to 1.618.

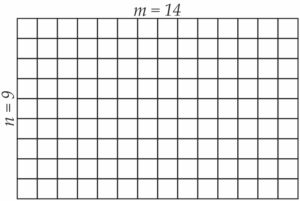
Remarkably, 1618 and 1000 played no special role in this reasoning, it works just as well with any two whole numbers m and n! Therefore: the golden ratio is not equal to any fractional number m/n, or equivalently, a golden rectangle cannot be partitioned into finitely many equal squares in the above way! A truly mind-blowing result! For, these squares can be as tiny as we want, even the size of a meson!² Again, between any two fractional numbers, howsoever close, there is an infinity of fractional numbers, yet, on this already more than overcrowded ruler, there is somehow still some room left for numbers like the golden ratio that are not fractional!

There is much more that can be said about this argument but I’ll move on now to a water feature, located on the other side of the front door, past that garden path, roman aqueduct, overhead water tank, and rockery with a stony brook hurrying down through its bonsai, cacti and whitewashed temple into that small water pond.

---

“Beesmukhi”

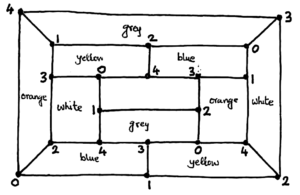
“Beesmukhi” (bees = twenty, mukhi = faced) is what its Bhojpuri-speaking sculptors called the concrete statue in this small water pond. It depicts–-once we have sublimated those concrete rods into zero thickness edges in our boundless imagination and put down a triangle of our own into each triangular boundary–-an icosahedron (icosa = twenty, hedron = faced), that is, a regular solid having 20 equilateral (all 3 sides equal) triangular faces, with 5 faces at each of its (20 \times 3)/5 = 12 vertices. We also see, thanks to the omission of the faces (triangular glass panes were considered briefly), the ‘innards’ of this statue, which reveal the secret of an icosahedron’s existence: its 12 = 3 \times 4 vertices are the vertices of 3 identical rectangles (those concrete slabs) each inserted perpendicularly half-way through a parallel central slit of the next in cyclic order (see the line drawing accompanying this photo, the cyclic order is I, II, III, I)!

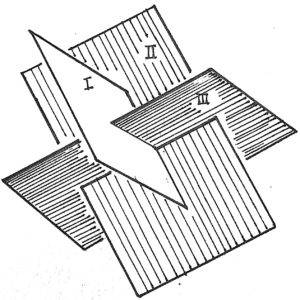
To verify this, we note that the 12 vertices are equidistant from the common centre of the 3 rectangles; and each is incident to 5 edges (concrete rods), while each edge has 2 vertices, so there are in all (12 \times 5)/2 = 30 edges. Of these, the 24 which join a vertex to one of the two nearest vertices of the next rectangle have clearly, by symmetry, the same length a. Also, the remaining 6 edges, being the shorter sides of the identical rectangles, have the same length b. In general, a is not equal to b, and only 8 of the obtained triangles are equilateral with sides \{a, a, a\}, the remaining 12 are only isosceles (two sides equal) with sides \{a, a, b\}. However, the above construction gives an icosahedron, provided the three identical rectangles have a special length-to-breadth ratio. For, if we keep b fixed, then a increases or decreases with l, the common length of the rectangles, being patently much bigger than b when the rectangles are very long, but is lesser than b when the rectangles approach `squarehood’ (the angle between the equal sides of the isosceles triangles is then almost a right angle), so there is an optimal l at which a = b.

Once again, it is time to move on, so I won’t elaborate further on the above argument, and shall only mention without proof that the above `special’ ratio turns out to be none other than the golden ratio! Which reminds me, we should have (because syntactically correct oxymorons are a dime a dozen) proved the existence of a golden rectangle also, not gullibly accepted its defining prescription at face value (and the missing beauties of the next `lecture’ shall drive home this existential point further)! Luckily, this particular oversight is easily rectified. We note that, the length-to-breadth ratio, of the rectangle obtained by deleting a square on a smaller side from a rectangle with fixed breadth b and shrinking length l, is equal to 1 when this varying length is 2b, and becomes arbitrarily large as l approaches b, so there is an optimal length l at which the rectangle obtained after deletion has also the same ratio l/b.

Also, here explicitly is the omitted general prescription for a regular solid \{p,q\}: its finitely many vertices should be on a sphere, its faces should be equal (regular)–-i.e., with consecutive vertices equally spaced on a circle–-polygons with p sides and vertices, and there should be q of these faces at each vertex. Clearly, p and q must be whole numbers 3 or bigger, and there exists a regular polygon with p sides for any such p, so, from the delicate way in which we settled the case \{3,5\} (icosahedron), it is natural to fear that the general existence problem for regular solids must be hard. Surprisingly, this is not the case, but, since it would be best to first meet the Egyptian beauty (no, not Cleopatra!) which inspired this unexpectedly easy solution, let’s move on a bit, past this glorious sextet of golden barrels–-which is almost as old as this fifty-year-old house–-towards that small gate, and look back at the new addition on the roof.

“Pyramid”

The four topmost glass panels suggest a small pyramid with a square base and equilateral triangular sloping faces, but only two of these extend to those much bigger but similar sloping triangular walls of glass, so, more imaginatively, you might like to think in terms of a bigger pyramid of the same kind that has only managed to free itself partially from the confines of the edifice! The remaining walls of this stair-head room, dubbed Kutiya (cottage) by the carpenters, are mostly opaque and plumb, and its interior is ‘ethnic’ and spartan: brick and salvaged (circa 1958) marble-chips flooring, raised sitting area also in brickwork with in-built chessboard, etc.] A quick continuity argument confirms that, if the apex is at a suitable height–-in fact at a height equal to the radius of the base–-above the centre of the square base, then the sloping and obviously isosceles triangular faces of the pyramid shall be equilateral.

More generally, for a variable pyramid, with base a fixed regular polygon Q with q sides, and apex A moving up and down on the perpendicular line through the centre O of the base, the angle \alpha subtended at the apex by a polygonal edge takes all values less than 360/q degrees, and only these values. For, the equal edges of this isosceles triangle (see figure) become very long, so their included angle \alpha becomes very small, as A recedes towards infinity, while \alpha increases towards 360/q when A approaches O. (In particular, since 60 is less than 360/4 = 90, there exists a square pyramid for which \alpha is 60 degrees, i.e., one with sloping isosceles faces equilateral.)

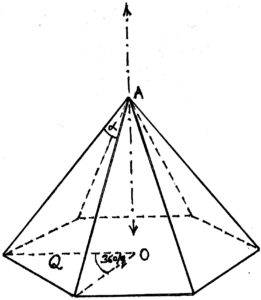
This generalization was motivated by the fact that a regular solid \{p,q\} can exist only if there exists a pyramid of the above kind with \alpha equal to an angle of a regular polygon with p sides. Indeed, any pyramid with A as a vertex of \{p,q\} and vertices of Q equidistant points on the q incident edges shall do the job.

We invoke next the `theorem’ that the sum of the angles of a triangle is a straight angle (180 degrees), which you probably still remember from school. If not, you can safely take it on faith, for it is logically equivalent to Euclid’s fifth postulate, the main unproved `axiom’ of his geometry. Now that Euclid’s name has come up, let me remark that all these beautiful things that I’m telling you about, about golden rectangles and regular solids and pyramids and such, they are all in that great treatise on geometry that was written by this Egyptian, virtually under the shadow of the Great Pyramid, about two to three centuries before the advent of the fair and beauteous Cleopatra! Coming back to our problem, we note that a regular polygon with p sides can be cut up into p-2 triangles, so the sum of its angles is (p-2) \times 180 degrees, so each is ((p-2) \times 180)/p degrees. Therefore, a regular solid \{p,q\} can exist only if ((p-2) \times 180)/p < 360/q, a very strong constraint indeed, for this inequality can be rewritten

\[\begin{align*}
q(p-2) &< 2p\\ qp – 2q – 2p &< 0\\ qp – 2q – 2p + 4 &< 4, \\ (q-2)(p-2) &< 4, \end{align*}\] i.e., the product of the whole numbers q-2 and p-2 must be less than four, i.e., \{p,q\} = \{3,3\}, \{3,4\}, \{4,3\}, \{3,5\} or \{5,3\}!

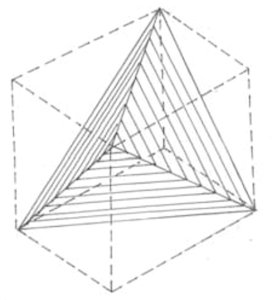
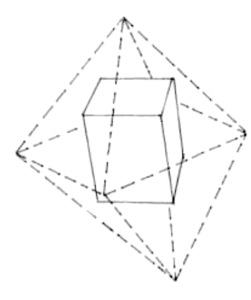
To mop up, note that, given any \{p,q\} we can make a \{q,p\} as follows: for each vertex of \{p,q\} take the regular polygon whose vertices are the q centres of the incident faces, the solid enclosed by all these polygons is a \{q,p\}. We already know that \{3,5\} or an icosahedron exists, and pasting (see figure) together the bases of two equal square pyramids with equilateral sloping faces gives us a \{3,4\} or an octahedron (eight equilateral triangular faces, four at each vertex). So by this method, we can also make a \{5,3\} or a dodecahedron (twelve regular pentagonal faces, three at each vertex) and a \{4,3\} or a hexahedron (six square faces, three at each vertex), respectively. The otherwise so rich English language has, very curiously, a popular synonym, cube, only for the regular solid \{4,3\}! Even the simplest regular solid \{3,3\}, which can be realized by choosing any four mutually non-adjacent vertices of a cube (see figure) goes only by its rather pedantic name, tetrahedron (four equilateral triangular faces, three at each vertex).

These five beauties are all there in this house! That “white-washed temple” on the rockery was a \{3,3\} (did you notice?), and we’ve discussed “Beesmukhi” = \{3,5\} at length, and this glass “Pyramid” (believe me!) is really the tip of a big \{3,4\} trying to free itself from the confines of this edifice. On the first-floor terrace, there are the Eyes (see photo) or the skylights of that new and skew ground-floor living room. These depict the two pieces of a \{4,3\} (cube) that one obtains when it is cut perpendicularly to its main diagonal, and there is much of interest that can be said about these hexagonal sections, as well as the grills showing beneath them. The \{5,3\} is also in the house, but as befits its special metaphysical significance, in a different avatar.

To explain this rather cryptic remark, I recall that Aflatoon (i.e. Plato, in Punjabi) had associated \{3,3\} with Fire, \{4,3\} with Earth, \{3,4\} with Air, \{3,5\} with Water–-the `Four Elements’–-and \{5,3\} with the Universe which contains everything as well as the Quintessence of everything (One is All, All is One). Even as metaphysics, this association looks somewhat arbitrary, for, we saw that \{p,q\} and \{q,p\} are practically the two sides of the same coin, then why are their associates so different? However, mankind always has, and always shall, try–-with of course varying success–-to find in mathematical certainty the basis for all sorts of beliefs and facts. Indeed, a large number of today’s theoretical physicists seem to be (if not openly declared, then closet) Platonists. For instance, with just a wee bit of poetic license one can say that `the special Lie group E_8,³ in the symmetries of which string theory is currently seeking the truth about quarks⁴ and practically everything else, is nothing but a higher-dimensional regular solid. Aflatoon would have approved!

“Miss Universe”

That wall-painting with the bevelled frame under my office window depicts a `topologist’s dodecahedron’. Exactly one of the four sides of each cemented panel is subdivided into two by a fifth vertex, so these panels are non-regular pentagons. Further, 5 different colours have been assigned to 5 pairs of panels, but the eleventh panel is left uncoloured, which should alert you to the fact that there is a twelfth face, which is–-of course!–-the obviously uncoloured and missing `glass pane’ in front of this painting. With this understood, you can check that there are, at each of the 20 vertices, exactly 3 of these pentagonal faces, so what we have here is a rather severely squashed \{5,3\}. Yet, this distortion is mild enough, and of no import, to a topologist, i.e., `a person who can’t distinguish between his/her coffee-cup and doughnut’.

More seriously, topology is an extreme generalization/ simplification of Euclid’s geometry in which distance and angle become bit players, only continuity matters. Accordingly, two shapes are topologically equivalent if there exists a one-one onto correspondence between them which is continuous in both directions. So a `topologist’s polygon’ with p sides may not (unlike the pentagons of this mural) even be planar, and its specified p boundary edges, joining one after another of its specified p vertices, can be very crooked. This implies that a closed surface bounding any reasonably smooth body admits (infinitely many) polygonal subdivisions into finitely many topologist’s polygons. By choosing one point (these shall be the vertices of the new subdivision) in each face of a polygonal subdivision, and for each pair of faces having a common edge a curve (these shall be the edges of the new subdivision) across this edge between the two points, we get a dual polygonal subdivision of the same surface with each face containing just one vertex of the original subdivision. For example, this construction applied to the mural above would give us a `topologist’s icosahedron’ \{3,5\}'. More generally a `topologist’s \{p,q\}'shall be any reasonably smooth body with a polygonal subdivision of its bounding surface into finitely many topologist’s p-sided polygons, q of them at each vertex.

Topology frees us from the shackles of Euclid’s fifth postulate, which had a decisive say in the last argument, so it seems there can’t be just five possibilities, with p and q at least three, for which one has a topologist’s \{p,q\} on a ball? However the answer remains “yes”, but there are brave new worlds (to wit, pretzels!) on which the remaining lost beauties \{p,q\} dwell! We denote by V, E and F the number of vertices, edges and faces of a polygonal subdivision of a surface. If it is a topologist’s \{p,q\}, each face has p edges and each vertex belongs to q edges, while each edge belongs to 2 faces and has 2 vertices, so pF = 2E = qV = say t, so V - E + F = t/q - t/2 + t/p = t(2p - pq + 2q)/2pq. Therefore, if V - E + F is positive, then pq - 2p - 2q is negative, which implies (assuming that both p and q are at least three) as before the same conclusion, viz., \{p,q\} = \{3,3\}, \{3,4\}, \{4,3\}, \{3,5\} or \{5,3\}. At first sight, our new hypothesis appears useless, but looks can be deceptive! The number V - E + F is the same for all polygonal subdivisions of a closed surface, i.e., it is a topological invariant of the surface, and can be easily computed by using any convenient polygonal subdivision of the same.

To get a feel of the proof, subdivide any polygonal subdivision with V vertices, E edges and F faces further by putting a new vertex (a) inside a face with u edges and joining it to the vertices of this face, or (b) on an edge and joining it to the vertices of the two, say u-sided and v-sided, faces to which the edge belongs. In case of (a), the new subdivision has V + 1 vertices, E + u edges and F + u - 1 faces, while in case of (b), it has V + 1 vertices, E + u + v - 3 edges and F + u + v - 4 faces; so V - E + F stays put under both operations. The required invariance is then a corollary of the fact that any two polygonal subdivisions P and Q of a surface are related to each other by a finite sequence of polygonal subdivisions P = P_1 , P_2, \cdots, P_n = Q, such that at each step, either P_{i+1} is such an elementary subdivision of P_i or vice versa.

In particular, V - E + F = 2 for the five regular solids, which are topologically equivalent to a ball, so this formula holds for any polygonal subdivision of its surface. The lost beauties can only be on surfaces whose V - E + F is non-positive, and one such we’ve already mentioned, viz., the surface of a doughnut or a coffee cup or, if you please, a pretzel with 1 hole. It has V - E + F = 0 and the two figures below depict a \{4,4\} and a \{6,3\} on it. More generally, the surface of a pretzel, or a block of wood, with t holes has V - E + F = 2 - 2t, which is a very negative number if t is very big, which prompts the query: can all the missing beauties \{p,q\} be found on surfaces of pretzels? As we’ll see later, the answer is “yes”, and just like Plato’s five, these \{p,q\}s are also geometrically regular, if we are willing to use distances not satisfying Euclid’s fifth postulate!

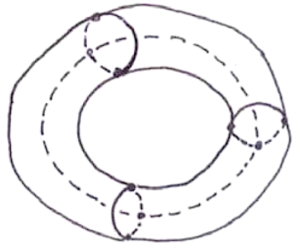
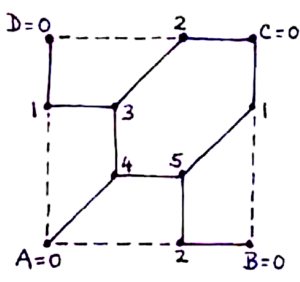
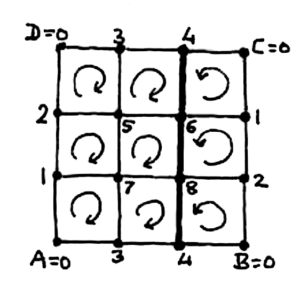
In the last figure, we used the fact that the surface of a doughnut can be obtained by glueing opposite sides of a square: AB \equiv DC converts the square into a cylinder, and AD \equiv BC corresponds to bringing the circular ends of this cylinder together in space. If we alter our glueing slightly to AB \equiv DC and AD \equiv CB something very remarkable happens: we obtain (in our imagination) a shape, called Klein’s Bottle, which is locally just like any closed surface, but which cannot possibly exist in three-dimensional space! To see this, note that if we put a circular arrow, on each face of a polygonal subdivision of a closed surface, which is clockwise when seen from the direction of the enclosed body, then each edge occurs with opposite directions with respect to the arrows on its two faces, but Klein’s Bottle does not obey this condition, for example, the choice of arrows depicted in the next figure is bad on the heavy edges. We can hope to find Klein’s Bottle only in a higher-dimensional Euclidean space!

Just so there is no confusion here, let me emphasize once again that geometry is really played out in the mind, it is a logical development of some axioms, and its admittedly helpful, but necessarily imperfect figures are quite dispensable. One goes from two- to three-dimensional space simply by postulating a new direction perpendicular to the old ones, and using this device again and again, we can do Euclid’s geometry in 4, 5, or as many finite dimensions, n, as we like. We’ll denote this Euclidean n-dimensional space by \mathbb{E}^n, and connected and closed shapes which topologically are just like \mathbb{E}^n locally shall be called n-dimensional manifolds. Examples: an n-dimensional sphere \mathbb{S}^n, i.e., a subset of \mathbb{E}^{n+1} consisting of all points at a fixed distance from a fixed point; again, any closed surface of Euclidean three-dimensional space is a two-dimensional manifold; but so too is Klein’s Bottle; likewise, by glueing pairs of faces of a subdivision of the surface of a ball one can obtain many three-dimensional manifolds, above all, Poincaré’s manifold P^3, which can be obtained from the body bounded by this bevelled wall-painting and its `glass pane’ by identifying the six like coloured pairs of faces as above.

Whatever one might think of Plato’s \{5,3\} = Universe/Quintessence–-or its `improvement’ \{5,3\}/\{3,5\}= Universe/Quintessence?–-this offspring P^3 of \{5,3\} has been at the centre of the topological universe for a hundred years and more! It was known that \mathbb{S}^2 was the only two-dimensional manifold in which every loop was bounded. For some time, Poincaré thought that a like statement was true in dimension 3, till he found P^3, which has this property but, unlike \mathbb{S}^3, is not simply connected: it has loops which cannot be shrunk to a point. Thus was born Poincaré’s Conjecture–-`a simply connected closed 3-dimensional manifold is topologically equivalent to \mathbb{S}^3–-the (erstwhile) holy grail of topology which spawned numerous beautiful results and finally a solution by Perelman so natural that it promises much more. Or, for that matter, take the embeddability of P^3 in \mathbb{E}^4 which (unlike the embeddability of the Klein Bottle in \mathbb{E}^3 that we disposed off in short order!) turned out to be extremely delicate: the answer is “no” if the embedding is required to be the slightest bit reasonable. Nevertheless, Freedman showed that there is a very crumpled copy of P^3 in \mathbb{E}^4, and this unexpected “yes” unlocked the door to the complete classification of simply connected 4-manifolds! I’m sure the last few sentences have gone completely above your head; to be quite frank, I don’t really understand all this myself, all I know is that there is scintillating beauty here, but despite trying off and on, I’ve only caught glimmers of it so far, but enough to keep on trying.

Uncannily enough, this offspring P^3 of “Miss Universe” has also been weighed by physicists as the global shape of the spatial universe–-one can almost hear Aflatoon’s “I told you so!”–-as revealed to us by those mysterious radio waves constantly coming to the Earth because of that `Big Bang’ aeons ago. However, I’m sure Plato would have been more impressed by what mathematicians have gotten out of his beloved \{5,3\}. To my mind, there is nothing in any other field which is remotely as deep or attractive.

---

The following is based on tea-time conversations–-for example, in this `new and skew’ room I mentioned before–-with parents of school-going children and others.

A common reaction to these `lectures’ is that they are unlike any my listeners heard in school or college. At which I blurt out that, at least in all of India north of the Narbada (the Narmada river), this is the common reaction to anyone saying anything mathematical in any manner. The unfortunate fact quite simply is that the “mathematics” which is being taught, learnt and done in our schools, colleges and even universities, is as close to mathematics as Johnny Walker’s “chan-chen chin-chon-chun” is to Chinese!⁵ The tail constantly wags the dog in these parts, and the baby gets thrown out with the bathwater every day: “mathematics” means monotonously memorizing methods for mindlessly doing the stereotypical questions in that looming examination at the tail-end of the year, and reasoning–-such a waste of precious time!–-finds no place in this inane and often panic-stricken drill.

Mathematics is all about formulating and trying to reason out solutions of clearly stated logical problems. Crosswords, chess or bridge problems, and sudokus qualify–-and some fine mathematics is indeed tied closely to games–-but more attention is rightly paid to logical issues and problems that have arisen from our attempts to understand more basic things like space, time, and motion. To my students confused about this word, I always used to say: `proof’ simply means `the reasons why’ and you all know what that means! For example, when someone asks “why are you carrying an umbrella?” you go “because it was raining earlier” if that happens to be your reason, it’s that simple! You have to do exactly the same, no less no more, that is, just clearly give your reasons in simple everyday language, if you want to fully answer any question in this subject; put another way: there are only `proof questions’ in mathematics, none other! Their classification into sums, examples, exercises, problems, propositions, lemmas, theorems and so on, is done in your book only for organizational purposes–-a highlighted theorem is likely to be used again, an exercise probably not–-and does not indicate any basic difference in the way in which their answers have to be penned: the reasons why, that is, a proof, is always a must! And neither is this classification a reliable indicator of difficulty: a prominently displayed theorem may be easy to prove without looking at the argument given in the book–-always a wise policy to adopt till a problem has utterly defeated you!–-while a nondescript exercise might have you running around in circles for many days or even weeks. Also, I used to repeatedly remind my students: mathematical symbols are convenient abbreviations meant to shorten sentences, not a license to murder them! Your argument, whether right or wrong, complete or incomplete, should at least be in grammatically correct sentences. Just like a string, say, e.g. et al. \$ etc. @ \% op. cit. i.e., of ordinary abbreviations all by themselves, is gibberish (unless you are writing in some code to a fellow-spy) so is almost certainly that extended string of mathematical symbols without any ordinary words between them which you handed in as your answer (unless you and your teacher are two computers who are communicating with each other using a purely symbolic language). If you can’t read out the full form of what you just wrote as an ordinary grammatically sound sentence, then you need to rewrite it. Indeed, in my humble opinion, it is almost always a good policy (especially so for a beginner) to try to use the minimum amount of notation, our mathematics tends to become that much better; anyway, there is certainly no direct correlation between the density per square inch of mathematical symbols and the quality of mathematics!

On the other hand, I am all for a liberal use of another kind of abbreviation–-a picture speaks a thousand words!–-in teaching, learning and doing mathematics. Indeed, via just four motifs and some quickly-drawn related sketches, I’ve conveyed to you, in next to no time and without any jargon, essentially complete proofs of some very famous results of mathematics.⁶ That I have gone easy on name-dropping was partly because of lack of time, but more out of a fear that you may not confuse the rose with a name, or for that matter a picture, of the rose. Such admonishments are no longer necessary if you have grasped the beauty of the patterns of thought, that is, the mathematics evoked by these motifs. Why, you are smelling the rose now! Your richly deserved reward for the effort that you have put in: mathematics is never a spectator sport, one has to do some mental work of one’s own even to `see’ already-done mathematics. Were my motifs merely making statements, they would have demanded much less, but this was not my intention, and non-trivial effort is sometimes needed to understand even some points of an argument which are labelled `obvious’, `clear’ or `trivial’! These `trivial’ gaps are inevitable in almost any argument of a readable length, and until and unless these missing steps also become clear to you, you obviously have not grasped the argument. Yes, reasoning correctly is the same as redefining things–-if `things’ means finite sets of statements and `redefining’ addition or deletion at each step of a statement which follows trivially from the others–-but mathematics is more: it is the art of redefining things, for example, Euclidean geometry is a never-ending logical thumri⁷ on just one non self-evident statement, the fifth postulate! Here too, a part of the kick, a great part I think, lies in the suddenness with which yet another lovely and unexpected reformulation arises ever so often out of nowhere, as is exemplified by some gems of this art-form that I have chosen to submit for your consideration via these motifs.

To really appreciate mathematics, one has to `do’ mathematics. If you are game, you can start trying today, and no prerequisites are needed, for, there are all sorts of logical problems, more natural than crosswords and sudokus, so more typical of what mathematicians prefer to think about, which can be found aplenty, and at all levels, from the internet or elsewhere.<sup>8</sup> If you are the sort who doesn’t give up easily, then pretty soon will come the day when you’ll be able to tell the world of one which was, oh-so innocent-looking, yet led you such a long and merry dance, before it finally revealed its secret, but not before you had a rather inspired idea of your very own! Then, and only then, shall ye know why, to those who are intensely involved in mathematics, its beauty is palpable! There is no silver bullet, but personally, I try to understand most problems via pictures–-a suitable figure being already the battle half-won!–-and find the same helpful in explaining my solutions. However, I must warn you that a figure not suitable for the task in hand can just as easily lead us astray, and there are times when those underlying patterns of thought can be `seen’ better and more easily without any visual aid.

Obviously, hard work is a must, but don’t do maths `seriously’: it is only a game! A mathematician at his most creative is like a child `in the zone’ with his video-game: as J.L. Synge has suggested, “the human mind is at its best when playing”! So this it’s-only-a-game approach may, just may, increase your chances of solving that problem. Besides, it has the extra bonus of softening the disappointment of failure, which–-let’s face it–-is always a distinct possibility whenever we do anything worth doing. Pertinent too perhaps is the fact that mathematics is a game–-just like say “dots and squares” (which shall occur in a motif below) but with more symbols and moves–-in the precise sense that mathematical statements can be written (though often very cumbersomely) as sentences of a purely symbolic language, and mathematical proofs can be written as finite (but usually extremely long: it would take reams of paper to actually write out some very simple arguments this way!) sequences of these symbolic sentences, each produced from the sentence preceding it by one of a handful of prescribed moves.

As we walk now after our cuppa towards the staircase, I note that walking in the opposite direction towards the skew room–-see the last two pics, right to left–-one has the pleasant feeling that one is in a moving ship turning left! Also, I recall our structural engineer’s “easy method” for calculating the area of this room or any quadrilateral: multiply the average lengths of the two pairs of opposite sides! Easy, but easily seen to be wrong, after which I’d asked–-this is typical of mathematics, one question leads to another–-as to exactly which were the quadrilaterals for which it was correct, which had led in turn to the roof-top motifs that we’ll discuss next.

Emerging out now from the “Pyramid” stair-head on to the roof-top, and looking down over its parapet, we can espy the first-floor sundial “IX to V” and way back, atop that roman aqueduct you saw before, a brand-new little white house which bing has built for himself… but I’m getting ahead of myself here… let me return to the motifs on the roof-top.

“Four half-turns”

The area of a rectangle is length times breadth, using which one sees that the area of a triangle is half the perpendicular from a vertex to the opposite side times the length of that side. Which in turn shows that, if we deform a quadrilateral by bodily translating a diagonal parallel to itself, respectively parallel to the other diagonal, then the areas of the triangles on either side of this diagonal, respectively the other diagonal, stay put. Therefore, the area of a quadrilateral stays put under a deformation effected by any translation of a diagonal. In particular, a translation B'D' to BD after which AC and BD bisect each other, converts any given quadrilateral AB'CD' to a parallelogram ABCD (opposite sides parallel and equal) of the same area. By drawing two families of equally spaced parallel lines we now partition the entire plane–-see figure–-into congruent parallelograms, of which ABCD is only one, and use B \rightarrow B' and D \rightarrow D' to translate back the entire line containing BD to the parallel straight line containing B'D', so as to simultaneously deform a whole row of these congruent parallelograms back to the row of congruent orange quadrilaterals, of which AB'CD' is only one. Next, we observe that the two shaded triangles have sides of lengths \{AB+DC, AB', D'C\} and \{AD+BC, AD', B'C\}. Since any side of a triangle is less than the sum of the other two, it follows that, this deformation increases the average length of a pair of opposite sides of a parallelogram. For a non-rectangular parallelogram, the product of these averages was already bigger than the area, so we conclude that the “easy method” of calculating the area of a quadrilateral is correct only for rectangles, and in all other cases it gives a value which is strictly bigger than the actual area.

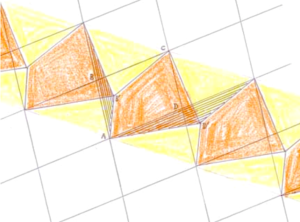
Besides, we have stumbled on a striking fact: the plane can be tiled by congruent copies of any given quadrilateral! To see this, we deform all parallelograms having `the same chessboard-colour’ as ABCD in the same way: the spaces left between the ensuing orange quadrilaterals will be congruent yellow quadrilaterals, namely, the fusions of the yellow triangles of each strip with those of an adjacent strip. Such a plane tiling is depicted (`building up’, as it were) on an island in the red brick roof-top. I note that, though the quadrilateral used in this motif is convex, i.e., with all angles less than 180 degrees, this was not needed in our proof, a non-convex quadrilateral tiles too.

As does any triangle, because two copies make a parallelogram; but all pentagons do not tile. For example, a regular pentagon does not tile the plane: all its angles are 108 degrees, and 108 does not divide 360, so no number of these can fit at a vertex. It seems it was Hilbert who suggested, more than a hundred years ago, that it shouldn’t be so hard to classify all convex pentagons which tile the plane, but the progress since then on this problem has been painfully slow and somewhat funny! A longish list of types of convex pentagons that tile the plane has been dressed up, and every 10–15 years or so, someone has claimed that the list was now complete, till someone else came along and cooked the said claim, simply by adding yet one more type, that had previously been overlooked, to the allegedly complete list! The analogous classification of convex hexagons which tile was much easier, and a short and indeed complete list is known since long; and, when the number of sides is more, it is easier still with list really short: the plane cannot be tiled by congruent copies of any convex polygon with more than six sides!

If a tiling has a symmetry relating any pair of tiles, then its symmetries are said to form a crystallographic group. Our quadrilateral tiling is of this type because, when a tile executes a half-turn around the mid-point of one of its edges, one obtains the tile sharing that edge with it, which (is an easy method for laying the tiling, and) shows that the Euclidean motion responsible for the (unique, because our quadrilateral has sides of distinct lengths) congruence T \equiv U between any two tiles must, automatically, map tiles to tiles! This symmetry is the composition of any sequence of planar half-turns taking our `dancing quadrilateral’ from T to U, so our group is generated by half-turns around the mid-points of all the edges of the tiling, but we’ll show more: our group is generated by the four half-turns \{p, q, r, s\} of a single tile! i.e., we’ll show that words in these four letters, interpreted right to left as compositions of the corresponding half-turns, give us all the symmetries of our tiling, it being understood that there is also an empty word 1 with no letters which represents the do-nothing (or identity) motion. However, the same symmetry is given by many words: we have the relations pp = 1, qq = 1, rr = 1, ss = 1 and pqrs = 1, and all their obvious consequences.

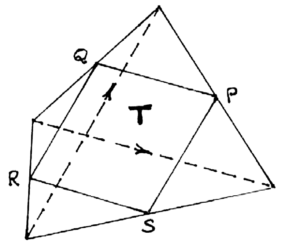
The first four relations merely say that doing a half-turn twice is the same as doing nothing. More generally, it is easy to check that a half-turn p of the plane around P, followed by a half-turn q around Q, is the same as translating each point of the plane by an amount equal to, and in the direction parallel to, the directed segment 2PQ. We’ll also need this pretty proposition–-see figure–-from school geometry: the mid-points \{P, Q, R, S\} of the sides of any quadrilateral T are the vertices of a parallelogram PQRS, whose sides are parallel to, and half as long as its diagonals. So pq = sr = t_1 , the translation by the directed diagonal 2QP = 2RS; so pqrs = srrs = ss = 1, the fifth relation; and qp = rs is the inverse translation by 2PQ = 2SR. Likewise, qr = ps = t_2, the translation by 2RQ = 2SP, and rq = sp is the inverse translation by 2QR = 2PS. The required result follows because, starting from this T, we can obviously reach any U by making, if need be, any one of these four half-turns, followed by a suitable number of translations t_1 and t_2 or their inverses.

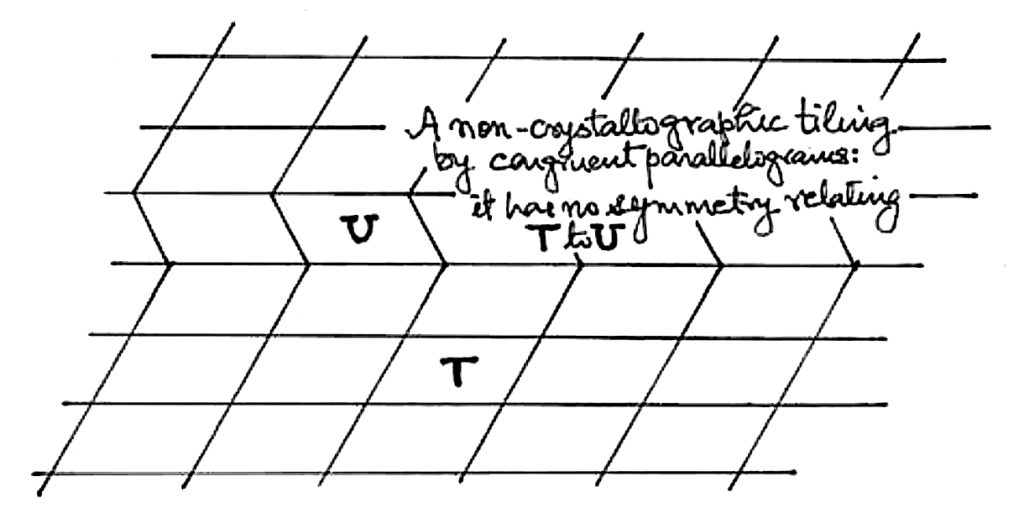
It has been known for two hundred years that, up to a composition-preserving bijection, there are exactly 16 more of these crystallographic groups! By 1900, the classification of the analogously defined spatial groups, which are the ones that really matter in the study of crystalline substances, was also essentially complete, there being now, exactly 230 spatial crystallographic groups! This had entailed arguments much more delicate than in the planar case, which led Hilbert to include, in his famous list of problems from that year, the determination of the crystallographic groups of Euclidean n-space, as the first part of his Eighteenth Problem. By 1930 or so, it was known that (like our two-dimensional example above) crystallographic groups of n-space are finitely generated and have n independent translations, and that there are only finitely many of these groups but this number is still unknown for n > 4.
The second part of the ‘Eighteenth Problem’ was about not necessarily crystallographic tilings, and had asked, amongst other things, for a particular three-dimensional example. From the fact that Hilbert did not ask for a similar planar example, it is likely that he had expected the answer “yes” to the following question: if congruent copies of a convex polygon tile the plane, then can they also tile it crystallographically? The second motif on this roof-top, that is, “Marjorie’s example”, shows that the answer is “no”!

Since one turns through 360 degrees as one goes around a convex polygon, the five angles of such a pentagon ABCDE obey A + B + C + D + E = (5 \times 180) - 360 = 540 degrees, and, in general, they obey no other condition. To make a tiling it is necessary–-otherwise, its copies won’t fit at a vertex–-that some of these angles, possibly with repetitions, should add up to 360 degrees. Again, it is necessary that some of the edges \{AB, BC, CD, DE, EA\} be equal: otherwise, the two tiles across any edge have to be reflections of each other, so we can tile only if the five angles are divisors of 360 adding up to 540, that is, never. A longish list of fitting conditions, sufficient for tiling, is now available.

The pentagon used here obeys the conditions B + 2E = 360, C + 2D = 360 and EA = AB = BC = CD that were shown by Marjorie Rice to be sufficient in 1975, and the fifth edge DE is shorter. So, in any tiling by congruent copies of this pentagon, one has triads of tiles like the one in the upper left corner. The reflection in DE is the sole Euclidean motion that throws the white tile of this triad on the one below it. For the tiling to be crystallographic, this reflection must map the third tile of the triad on itself, which is impossible because our pentagon is congruent to itself only via the identity map. So this is a counterexample to a conjecture of Hilbert’s; also, it is an example of what can be achieved by sheer enthusiasm! For Marjorie Rice, you see, was a housewife who had studied maths only till her high school thirty-five long years before, when she chanced one day upon an article on pentagonal tilings in the Scientific American that led her to start making more and more of these tilings on her own.

Footnotes

1. Also, I’ll now be able to refer my inquisitors to this article, which policy should, if nothing else, save those of our visitors who pose their queries more out of politeness than curiosity, from being bored to death by my possibly long-winded answers! ↩
2. Editor’s note: A short-lived subatomic particle made up of a quark and an antiquark. ↩
3. Editor’s note: E_8 is a 248-dimensional exceptional simple Lie group with an 8-dimensional maximal Torus. ↩
4. Editor’s note: Quarks are elementary particles that make up protons and neutrons. ↩
5. Bollywood comedians were and are prone to mimicking alien languages to raise laughs. A further note for mathematicians in developed countries: beware of drawing parallels with shortcomings in your own system, believe me, they are all insignificant in comparison! ‘The law of large numbers’ implies a few of us do manage to learn mathematics despite this system, and this tiny percentage then tends to drift to your shores; but in India itself, it is not this handful, but the mainstream of “mathematicians”–-a totally different species really!–-which is very much in control of the whole show from top to bottom. ↩
6. For example, the existence of non-fractional or `irrational numbers’ was proved by the Pythagoreans, and is still amongst the three or four deepest things in school mathematics; yet the proof which I’ve given in “Perfectly proportioned” is perfectly easy! Moreover, this pictorial method–-which, much to my bafflement, I’ve not seen used in any textbook!–-is quite general, and repeatedly deleting a square on the smaller side of a rectangle or `Euclid’s algorithm’ also gives us, when it terminates, the `highest common factor’ of the sides, or equivalently, the subdivision of the rectangle into equal squares of the largest size. Again, the theorem that there are five and only five regular solids, was the probable aim of Euclid’s long treatise, and comes at its very end, and is not even taught in schools and most colleges. The informal continuity argument which I used in “Beesmukhi” for the existence of an icosahedron (or golden rectangle) was used by Eudoxus in a more formal guise to define multiplication of lengths, similarity of triangles, to which topic the hardest of Euclid’s books, Book V, was devoted; and much later, in the hands of Dedekind in the nineteenth century, this `completeness property of the line’ led to a complete arithmetization of geometry, and people started calling the points of the number line `real numbers’. And so on. ↩
7. Semi classical Indian vocal music in which one typically repeats, virtually fondles, just one sentence, say a declaration of one’s love for Krishna, in wildly different ways. ↩
8. For example, the problems from the 2009 International Mathematical Olympiad, a competition for gifted high school students, are posted with my solutions to the same at my website on www.kssarkaria.org/docs/imo2009.pdf. ↩