We will now descend the stairs back to the ground floor, and exit towards the annexe, to view the line-mural on the northern wall of this house (but, for a really up-close view, we should have gone instead to the adjoining roof-top of the annexe).
“Grecian origami”
I’ll resist repeating in full a favourite story of mine about how I had tracked down a famous, but forgotten, mural of Jeanneret’s in this city about five years ago, but shall recall that his raised red-brick mural1 was in a state of advanced neglect (with almost two full letters missing) when I’d finally re-found it and hurriedly made that day the sketch that is shown below (for I didn’t have a camera on me). You’ll immediately recognize in its E + F = H the statement of the one theorem that we all remember from school!
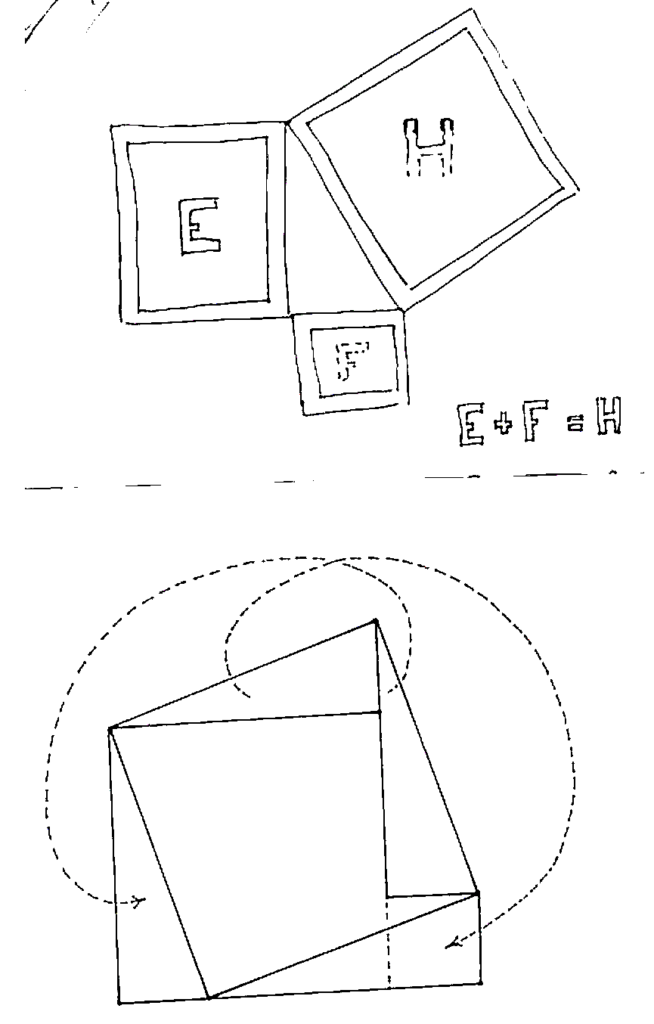Above that balcony with a `jeanneret jaali’—a knotted brick lattice de rigueur in Chandigarh houses built till the late sixties!—and a vertical version of a more traditional jaali once popular on the parapets of Punjab’s villages, there is a mural which is even simpler—grooves in cement, coloured purple—than Jeanneret’s, and scores over it in as much as it depicts the same theorem with a complete proof! Simply cut out—with scissors if you will!—the two congruent right triangles from the big tilted square on their hypotenuses, and translate the triangle at the top to the bottom, and the one on the right to the extreme left, to obtain that shoe-shaped union of the squares on the smaller sides, which can be cut further, if need be, into these two squares.
More generally, the paper-less Greek ancients knew that any finite set of polygons can be converted into a single square by paper-cutting and pasting (= `uncutting’) moves! Indeed, the mural has already taught us that a sum of two squares is equal to a square in the sense of this `Grecian origami’ (as against Japanese origami, which uses paper-folding and unfolding moves), and a polygon can obviously be cut into triangles, and a triangle converted easily into a rectangle, which can be cut into equal squares and a rectangle which is not too long (length by breadth \leq 5 will do). We cut such a rectangle parallel to its length and breadth to make four similar and equal rectangles, and lay these four as shown below, so it’ll suffice to show that this (shaded) difference of two squares is also equal to a square. To see this we check that, because our rectangles are not too long, the square hole can be rotated around its centre by any amount we like within the big square,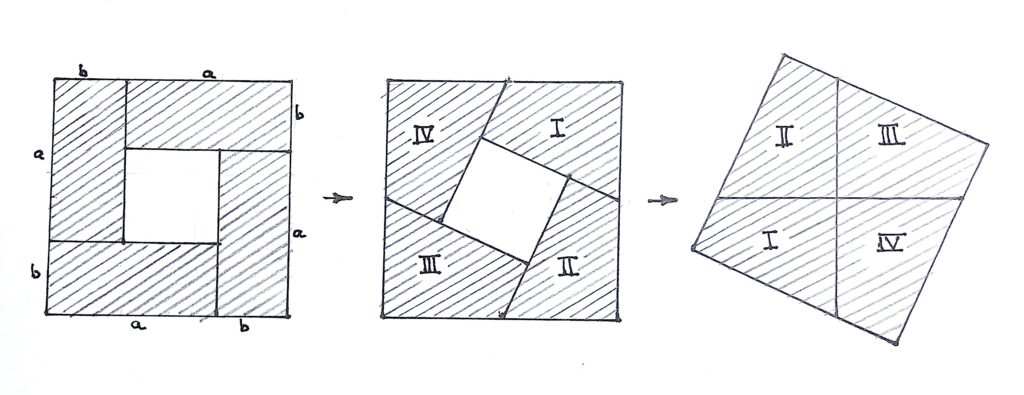
and that this rotation can be realized by cutting and re-pasting four equal triangles. We rotate the hole thus to the new position in which the clockwise extensions of its arms meet the edges of the bigger square at their mid-points, and cut along these extensions, then the resulting four congruent pieces shall refit to form a square.
A line segment and a polygon are also called, respectively, a 1-dimensional and a 2-dimensional polytope, and quite generally, an n-dimensional polytope is a region of n-dimensional space bounded by finitely many (n-1)-dimensional polytopes, and one can play n-dimensional Grecian origami with these! The Grothendieck group K(n) has as elements all finite sets of n-dimensional polytopes or their negatives, with two such sets deemed same if they are related to each other by pasting and cutting, and these operations are used to define addition and subtraction in K(n). This is a natural generalization of the geometric definition of numbers: K(1) is clearly the real numbers as defined in school with the usual addition, and it is easy to see that addition is associative, commutative, and obeys the cancellation rules in any K(n). The result we proved above shows that on K(2) too, there is a notion of `greater than’ which is well-behaved with respect to addition, and which is `complete’ (given any partition into two parts, with anything in the first less than anything in the second, exactly one of the parts has a greatest or smallest element), so, K(2) is isomorphic to the additive group of real numbers K(1). More precisely, there is a unique one-one, onto, and order- and addition-preserving signed-area map K(2) \to K(1) which assigns to the unit square the number 1. As against this, for n \geq 3, the groups K(n) are not totally ordered (but their structure is still not completely worked out for n \geq 5), so, there are 3-dimensional polytopes of the same volume which are not related to each other by any finite sequence of cutting and pasting moves.2
From our vantage point under this old mango tree, that we had chosen to view the Pythagorean mural, if you’ll now kindly turn, and peer out over the boundary wall, you’ll notice many copies of the last two drawings in the humble concrete of the “Pythagoras Drive” which a car needs to take from the main road to enter this house!
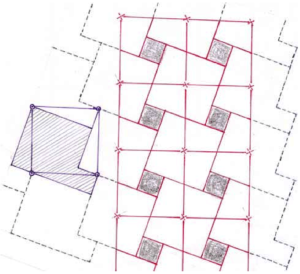As we walk out on this driveway, let me point out how intimately its red-brick pattern is tied with the mural, which is re-drawn on the right, with the big tilted square now shown straight-up, and I’ve shaded its shoe-shape, the better to display how congruent copies of this shoe, when translated vertically and horizontally by amounts equal to the hypotenuse, fit snugly with each other to give us a tiling of the entire plane! The crosses mark the centres of the bigger square constituents of some of these shoe-tiles, and by joining them one gets the big square panels of the driveway whose central black granite tiles depict the smaller square constituents, or the toes, of some of these shoes. While making this driveway, the tricky part was to lay these small granite tiles accurately, so that the clockwise extensions of their arms would hit the sides of the big panels in their mid-points; once this was done, the brick pattern was easy enough to complete, and then finally, concrete was poured into the remaining congruent quadrilateral spaces. Indeed, you must have noted some `warm-up panels’ of this driveway inside the gate, in which extensions are not required to hit the mid-points, e.g., there was one depicting the first of the trio of diagrams on the last page, which proves (a-b)^2 + 4ab = (a+b)^2.
It also solves the discrete Pythagorean problem, in which one seeks all pairs of squares made from square tiles of unit size, whose sum is also such a square. The diagram shows that the difference of two such squares, both even or both odd, is made up of a whole number of unit tiles, and is a perfect square if and only if ab is a perfect square; for example, a = 4 and b = 1 give the solution 3^2 + 4^2 = 5^2; a = 9 and b = 4 give 5^2 + 12^2 = 13^2; and so on. We can just as easily solve some higher-dimensional problems, e.g., is the sum of two cubes a cube in the sense of Grecian origami? Yes! Using two-dimensional origami (with the remaining dimension basically a passenger) we can convert the cubes, and the cube having the same volume as their sum, to boxes of height one; then, using two-dimensional origami again, convert the sum of the bases of the first two boxes to that of the third box. Repeating this, we see in fact that, the same is true for any two `n-dimensional cubes’, i.e., n-fold `powers’ of segments, in the same sense as a plane is often considered a `product’ of two chosen lines or axes. More generally, this Cartesian product defines a multiplication K(n) \times K(m) \to K(n+m) which is still not fully understood. However, K(1) \times K(1) \to K(2) followed by the area isomorphism K(2) \to K(1) is obviously the multiplication of numbers. However, the higher-dimensional analogues of the discrete Pythagorean problem are more challenging, and the general assertion that for any n \geq 3, the equation x^n + y^n = z^n has no solution in positive whole numbers x, y and z—which Fermat (in)famously could not leave us a proof of because there was not enough space in that margin—was proved, after all these centuries, in the early 1990s by Wiles, but we definitely don’t have enough space to explain his proof here!
Returning to the tiling that we’re standing on, I note that it is crystallographic with no symmetry other than its defining translations and that there are 8 vertices on each of its congruent shoe-tiles—the angles of this non-convex octagon are 270, 90, 90, 180, 90, 180, 90 and 90 degrees in clockwise cyclic order—but at some vertices, there are 3 tiles, at others only 2. Unlike, say, the usual brick pattern all over these walls, which depicts a tiling by non-convex hexagons, 3 at each vertex. So, in analogy with a question about polygonal subdivisions of surfaces that we posed in the section “Miss Universe,”3 we ask: is there a tiling of the plane by topological p-gons, q at each vertex? Note that we have thrown away all geometric shackles, our tiles are now allowed to be not only non-convex but practically arbitrary, and we aren’t demanding any congruence between them, let alone crystallographicity of tiling. Moreover, not being confined now to a closed surface of a bounded body—we have the plane’s infinitude at our disposal!—intuition suggests no obstruction, and it seems very reasonable to expect the answer `yes’. However some care is needed; you can soon find out for yourself, by just trying to build these tilings, that, the answer is `no’ for \{p,q\} = \{3,3\}, \{3,4\}, \{4,3\}, \{3,5\} and \{5,3\}:} you’ll be forced to go into the third dimension (and there you’ll get the same old examples)! For all other values of p \geq 3 and q \geq 3 the answer is `yes’, as we’ll see in the `lecture’ after the next, and then we’ll use our proof to solve the previous question about closed surfaces.
It is time to move on, but we won’t re-enter the house just yet, we’ll make a right turn on this sidewalk to take a look at that other driveway which goes till the main gate of “213, 16A”, for there awaits us, again in its humble concrete, our next motif (there is also some `concrete mathematics’, viz., a repeat of “four half-turns”, which can be seen outside the small southern gate of this house, which opens on the side street).
“Amazing curves!”
As you can see—a line-drawing and a roof-top view are also given—the same materials are used again: three square `islands’ are made from granite tiles of unit size, and around them swirls an extended red-brick pattern, which turns this driveway into a maze of concrete paths, complete with an arrow indicating its point of entry. Its two-dimensionality (no view-obstructing high hedges here!) renders this maze easy to thread, and I’ve seen many `children’ (of all ages!) go zig-zagging gleefully and triumphantly up this maze to the main gate, though it must be said that quite a few of them don’t know what that initial 11010101 in dark red brick signifies.
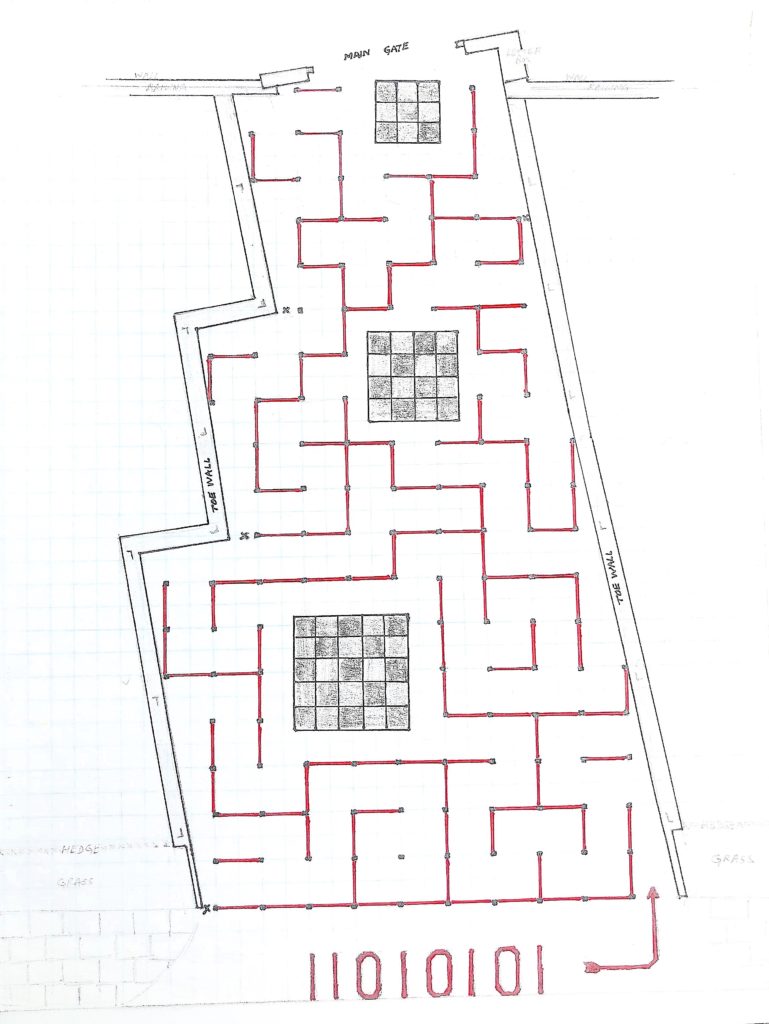
I’ll come to this in a little while, but first, I must urge you to look harder, for then you’ll realize (this is especially clear in the line-drawing) that something even more `childish’ has been going on here: a dots-and-squares game! Doubtless, you have played this game in school and/or college between (or maybe even during some particularly boring) classes, but here are its rules anyway. On a chosen playing area—a rectangular piece of paper usually, but here the region between these toe-walls converging to the main gate of the house, minus the three tiled islands—one marks all the vertices—here one-inch square dots of dark brick—of a square grid; then the players take turns putting in the edges—here one-inch thick in red brick—of the grid between them, with a player having the option of an extra turn every time he/she completes a square; and the winner, if any, at the end, is the person who has made the most squares. However, there is something peculiar about this particular game: no player has bothered to `take’ a square! Maybe the players are rank tyros, or maybe, though it is much less likely, accomplished grandmasters playing a deep cat-and-mouse strategy, for, after all, dots-and-squares is still unsolved? No, the real reason is something else again: the players have become so fascinated by an incredible thought tied closely to the emerging and meandering snakes of squares—in a typical game, each of these gets taken in one go towards the end, and these climactic moves usually decide who wins or loses—that they have lost their competitive edge entirely, and have started thinking of something much more interesting than who shall win or lose this silly game! Leaving you wondering for the moment as to what this `incredible thought’ could possibly be, I’ll finish the description by mentioning that—like that arrow, and the initial mysterious string of 1s and 0s—the four interdicting crosses in darker brick, that you see near the toe-walls, are there only to turn this peculiar game position into an appealing maze.
Long familiarity often makes us forget that whole numbers are abstractions (and it is this that makes them useful): sure, five ducks, five pens, five poems, etc., are tangible enough, but, as Cantor reminded us in the nineteenth century, five, of and by itself, is the commonality between, or alternatively, the equivalence class of all these sets, any two of which are related to each other by a one-one onto or bijective correspondence, and, when we think about it, it is nothing short of a miracle that a human child can intuitively grasp this abstract notion of `five’ in kindergarten: no other species even comes close! The usual notation for these notions is also interesting: for the first ten non-negative whole numbers we use the ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, and then, we denote any number by counting off powers of ten, from the highest downwards, in that number, for example, the number of this house has 2 second powers, 1 first power, and 3 zeroth powers of ten (a zeroth power is always unity by convention), and that’s what 213 signifies. However, the choice of ten as `base’, though customary, is in fact quite arbitrary: any number bigger than one would serve just as well (the choice ten was probably made because we have as many digits on our hands, but there have been ancient civilizations that got along just fine with other bases)! For instance, if we want to decrease the number of symbols, then the least choice, two, is obviously the best. Once again, let us agree to use 0 and 1 for the first two whole numbers, but after that, any other number will now be denoted by counting off powers of two— that is, 1, 2, 4, 8, 16, 32, 64, 128, and so on— from the highest downwards, in that number, for example, 11010101 is the house number in base two notation, because, as you can check, 213 = (1 \times 2^7) + (1 \times 2^6) + (0 \times 2^5) + (1 \times 2^4) + (0 \times 2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0).
There is a whiff here of “Pythagoras Drive” too: the three tiled islands depict the smallest solution of the discrete Pythagorean problem, 3^2 + 4^2 = 5^2. In this context, observe that an odd square has a central tile, an even square has none, and the number of tiles in each square ring is a multiple of four. So, the sum of two odd squares is not a square, a point tacitly used when we’d solved this problem; also note that in base four notation, using the letters a, b, c and d (instead of the more hackneyed 0, 1, 2 and 3 respectively), this observation translates into saying that the right-most letter of the word denoting an odd square is b, and that it is a for an even square.
Our dots-and-squares players, who were incidentally named Georg and David, had not neglected maths in school, so they knew that not only whole numbers, but, any non-negative real number can be written as an infinite decimal, and likewise, in other bases too, e.g., in base four. We subdivide the non-negative number line into segments (end-points are deemed in them) of unit length, and denote each of them by the base four notation of its initial whole number followed by \bullet (`decimal point’); then, we subdivide these segments into four equal segments, and denote them, respectively, by appending a, b, c or d to the notation of the subdivided segment; next, we subdivide these into four equal segments, and denote them, respectively, by appending a, b, c or d to the notation of the subdivided segment; ad infinitum. Having done this, we denote a real number x by [x_1 … x_t \bullet x_{t+1} x_{t+2} …]—where each x_i is either a, b, c or d; thus, except for that dot and the enclosing brackets, this is a right-infinite word formed from four letters—if and only if it is contained in all the segments denoted by the finite truncations of this infinite word, that is, x should be in x_1… x_t \bullet, as well as in x_1 … x_t \bullet x_{t+1}, as well as in x_1 … x_t \bullet x_{t+1}x_{t+2} etc. I’ve added the brackets to emphasize that some pairs of words are to be identified, for, to positive endpoints of all these segments, we have obviously assigned not one, but two words; this too is exactly as in decimal expansions, where, for example, we know that 13 \bullet 45000 … is to be identified with 13\bullet44999….
Now consider a snake of squares (boundaries are deemed parts of squares) of unit size that a dots-and-squares player can take thus: he puts in the final edge of the first square which also becomes the third edge of the next square, then he puts in the final edge of this square which also becomes the third edge of the next square, etc. The first diagram below shows five of the twenty squares en prise in the game on this driveway, which can be taken in this manner in the indicated order; but clearly, one has arbitrarily long finite snakes, as well as infinite ones that cover the entire plane. The `incredible thought’ they inspired was this: using a snake, one can label points of the plane, in a manner entirely analogous to the base four notation above for points of the line!
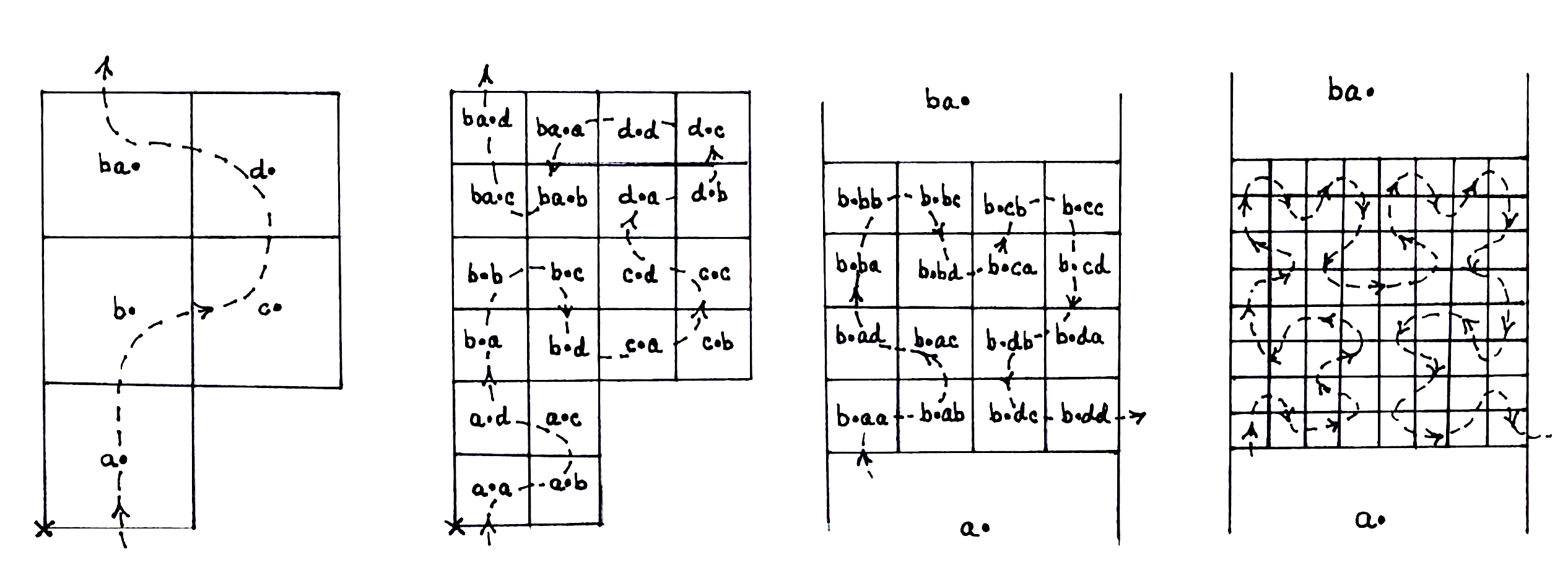
We denote the chosen snake’s squares, in order of capture, by the base four notation of the corresponding whole number followed by \bullet; this order is indicated by the dotted curve in the first picture, which starts from an extant edge with a crossed vertex on the first square. We now subdivide these squares into four equal squares, and build a snake—see the second picture—from all these: its first square is the one having the cross on it, then the other three in the first big square in the order which lets us exit it on the same side as before; then come the four small squares of the second big square in the order which lets us exit it on the same side as before; etc. (It is easily checked that the order indicated by the directed dotted curve of the second picture is the unique such order.) We denote the small squares within each big square, in this order, by appending a, b, c and d to the notation for the big square. Next, we cut up all these small squares into four equal and still smaller squares—because of congestion this step is shown in the third picture only for the square b \bullet on a magnified scale—and make, exactly as before, a snake from all these; and these are denoted by appending a, b, c and d in this order as before; and so on (things became so crowded that only the dotted curve indicating this portion of the next snake is drawn next, the names of the squares are omitted). With all these squares now unambiguously named (exactly like those segments were before) we make the parallel definition: we denote a point X of the plane by [[x_1… x_t \bullet x_{t+1} x_{t+2} …]] if and only if it is contained in all the squares denoted by the finite truncations of this infinite word, that is, X should be in x_1 … x_{t} \bullet, as well as in x_1 … x_t \bullet x_{t+1} as well as in x_1 … x_t \bullet x_{t+1} x_{t+2}, et cetera. The double brackets indicate that there is need to make more identifications now than in the one-dimensional case: to points X on the interiors of the edges of our squares we have assigned two words, but to those on the vertices, as many as four. Thus x = [x_1 … x_t \bullet x_{t+1} x_{t+2} …] \to [[x_1 … x_t \bullet x_{t+1} x_{t+2} …]] = X is well-defined but not one-one, and obviously X is varying continuously, i.e., is tracing a plane `curve’, as x varies, a curve which, amazingly, visits each and every point of all the squares of the chosen snake (these variations of X can, however, be shown to have no specified direction, so one can justifiably argue that this is an inappropriate usage of the word curve)!
This neat definition, of the younger player David Hilbert, generalizes painlessly to all dimensions n—one uses base 2^n now because an n-dimensional cube subdivides into so many cubes of half the size—to yield a continuous mapping of the unit segment onto the n-dimensional unit cube! For n \geq 2, this is magical: by identifying finite subsets of a segment we can increase dimension as much as we like! This was known already to the older player, Georg Cantor, who had given a (non-continuous) one-one onto map between a segment and a square, and had observed that the magic begins at n = 1: the space \mathbf{C} of all infinite sequences of 0s and 1s is zero-dimensional}, and becomes the one-dimensional segment only post those innocuous two-fold identifications of base 2 expansions! To see this zero-dimensionality, switch 1s to 2s and interpret these sequences of 0s and 2s as points of the segment in base 3, this exhibits \mathbf{C} as the `dust’ remaining after this: delete the middle third to get two disjoint segments, then delete their middle thirds, etc. The segment, the square, the cube, etc., so all the continuums like manifolds that one encounters in most of mathematics, can be constructed from this primordial Cantorian dust \mathbf{C} by making finite-to-one identifications! For, base 2^n expansions can be read off from the base 2 expansion. For example, the point 1101010011… of \mathbf{C} goes to the point x of the segment having base 4 expansion [\bullet(11)(01)(01)(00)(11)… ] = [\bullet dbbad …], which goes to the point X = [[\bullet dbbad …]] of the unit square defined by using a snake with one square, with say the top edge final; likewise, grouping terms in threes gives the base 8 expansion, so, by the generalized definition we mentioned, a point in the cube, etc. In all likelihood, Cantor already knew of a simpler, but less neat, construction of a continuous map from the segment onto a square: the base 2 surjection \mathbf{C} \to[0,1] induces a surjection \mathbf{C} \times \mathbf{C} \to [0,1] \times [0,1], but \mathbf{C} \times \mathbf{C} can be identified with \mathbf{C}, so by linearly extending this function on those deleted thirds we obtain a continuous surjection [0,1] \to [0,1] × [0,1]. Also, he most certainly knew that, C represents a bigger infinite whole number—in the sense of his definition of five given earlier—than the set of all finite whole numbers, because any one-one function from the latter to the former misses the sequence of \mathbf{C} whose n-th term is not the n-th term of the n-th sequence! Mathematics of today can all be written formally in set theory, the language which Cantor invented, and Hilbert and others developed, to talk expressly of these infinite whole numbers.
“Magic Carpet”
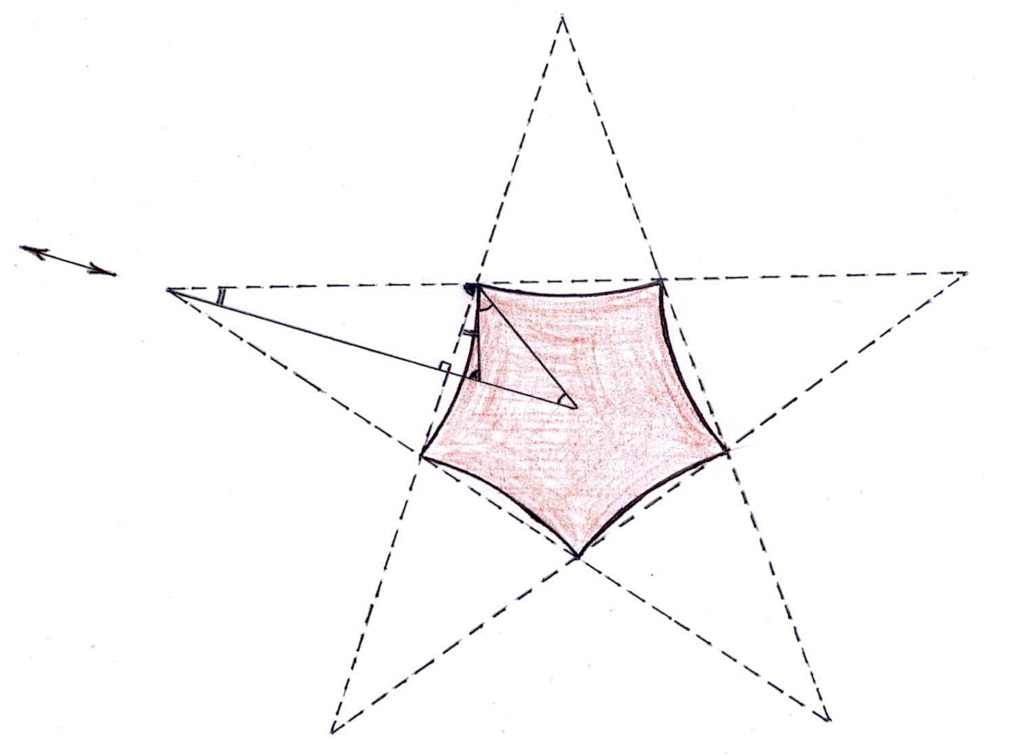
Now that you’ve traversed the maze, and are past the main gate, you’ll note that we’re back where this tour began: there, to the right on that wall in front, is “Perfectly proportioned,” which involved the golden ratio, after which we’d gone tripping down that stone path to the left to see “Beesmukhi,” whose three rectangles were golden too, which is the same as saying—consider the pentagon whose five vertices are the five neighbours of any vertex of this icosahedron—that the golden ratio is equal to diagonal divided by side for any regular pentagon. You’ll note also, if you look down, that you’re being given a red-carpet welcome, and that, in this welcoming mat that you’re standing on, there is again, a regular pentagon, but this time, one whose edges are circular arcs; as Poincaré showed, this seemingly frivolous frill has amazingly far-reaching implications!
More precisely, our five circular edges have as their centres the five vertices of the pentagram obtained by extending the edges of an ordinary regular pentagon, from which fact it follows—see the next diagram—that, the angle between the tangents to the two circular edges at each vertex is 72 degrees, that is, one-fifths of 360 degrees; and likewise, starting from an ordinary regular polygon with p \geq 6 edges, one gets a regular polygon with p circular edges making an angle of 360/p degrees at each vertex.
By moving their centres equally towards or away from the centre, we can make these circular edges more or less curved, so we see further that, for all p \geq 3 and q \geq 3, other than the five exceptions \{p,q\} = \{3,3\}, \{3,4\}, \{3,5\}, \{4,3\} and \{5,3\}, there is a regular polygon with p circular edges making an angle of 360/q degrees at each vertex. The five exceptions come about because we don’t want edges bending outwards, so 360/q cannot be bigger than the angle ((p-2) \times 180)/p of an ordinary regular p-sided polygon, and while discussing “Pyramid,” we’ve seen that this happens if and only if (p-2)(q-2) < 4, i.e., in these five cases. However, we’ve not excluded the cases when the edges are not curved at all, which happens if and only if these two angles are equal, i.e. (p-2)(q-2) = 4, i.e., \{p,q\} = \{3,6\}, \{4,4\} or \{6,3\}. In other words, we’ve adopted the convention that `a regular polygon with circular edges’ may, in particular, have straight edges; in fact, the key to the following is to, think of straight lines as if they were “infinite circles” passing through an additional “point at infinity,” for this intuition suggests rather naturally the appropriate generalization of some concepts to `all’ circles.
For example, the case \{4,4\} is that of a square, and the red half-brick square tiling that you see around the curved pentagon is `seen’ also by someone who has ensconced herself in a square changing-room with mirrored walls, which prompts this question: do multiple reflections in the circular edges of this single curved pentagon determine likewise a tiling by infinitely many curved pentagons, five at each vertex? The answer is yes (!) provided we define reflection in a circle suitably: the image of any point P shall be the point P' lying on all circles through P which cut the mirror perpendicularly.
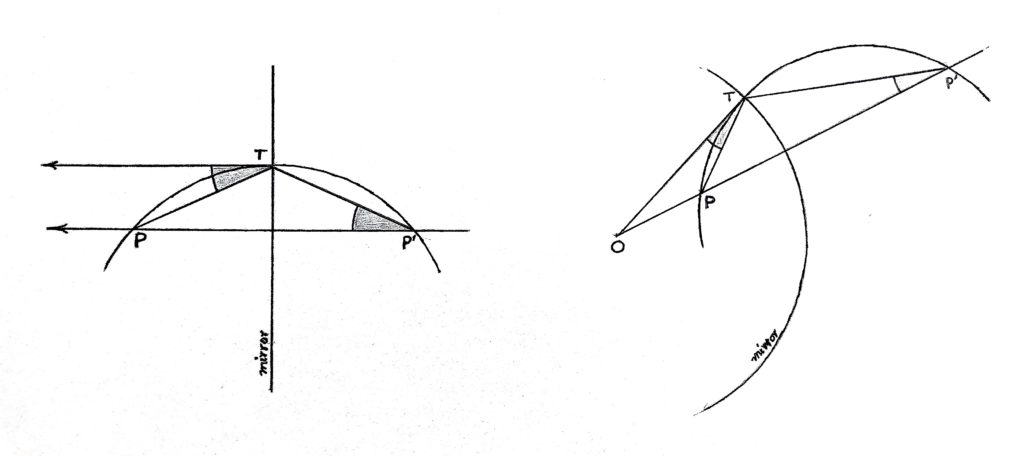So, reflection in a finite circle switches its centre O with the point at infinity, keeps its own points fixed, and preserves any perpendicular circle—say, a line through O—as a whole, but interchanges all pairs of points \{P,P'\} on it such that OP'\times OP is the square of its radius. For, a circle cuts the mirror perpendicularly at T if and only if OT is its tangent at T, i.e., OP'T is similar to OTP, i.e., OP'/OT = OT/OP, i.e., OP' \times OP = OT^2. The remaining circles are paired with distinct circles. If OU \neq OT is tangent to the circle at U—see diagram—then it expands/contracts to the circle obtained by multiplying all rays from O by OT^2/OU^2, because OQ \times OP = OU^2 and OP'/OQ = OT^2/OU^2 = OQ'/OP imply OP' \times OP = OT^2 = OQ' \times OQ.
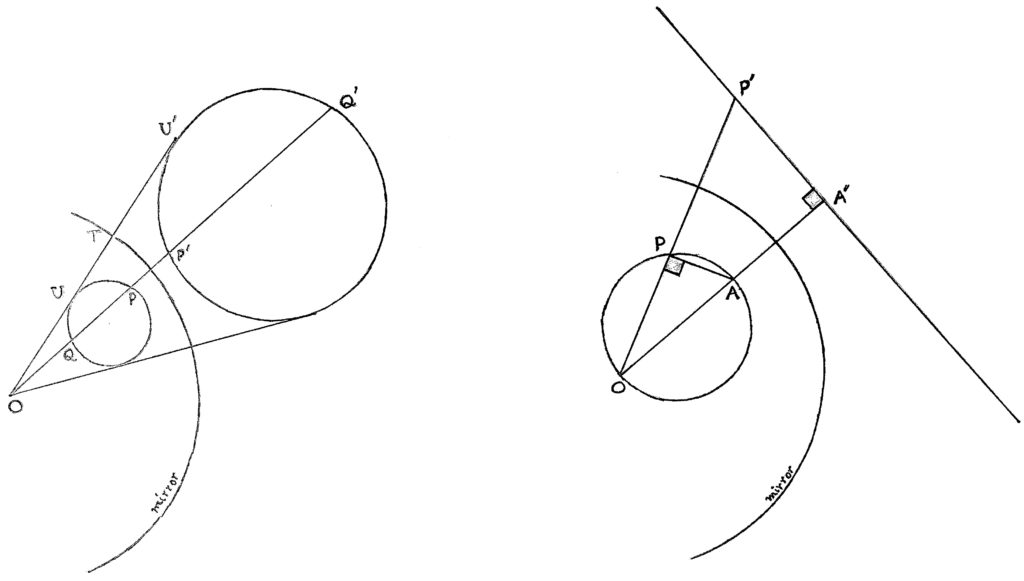Likewise, when O is inside the circle, then reversing and multiplying all rays from O by the constant OT^2/(OQ \times OP)—here, PQ is any chord of the circle through O—shall give the other circle. Finally, a finite circle through O gets paired with the line (infinite circle) perpendicular to the diameter OA at A', because the similarity of OAP and OP'A' gives OP' \times OP = OA' \times OA. Though not distance-preserving, reflection in a circle maps any angle at P to an equal but opposite angle at P': by continuity of P \to P', it suffices to check this off the mirror, when the circles through P and P' tangent to the two directions enclosing the given angle at P, being perpendicular to the mirror, are preserved by reflection in it, so the angle at P is mapped to the equal but opposite angle between these circles at their second intersection P'.
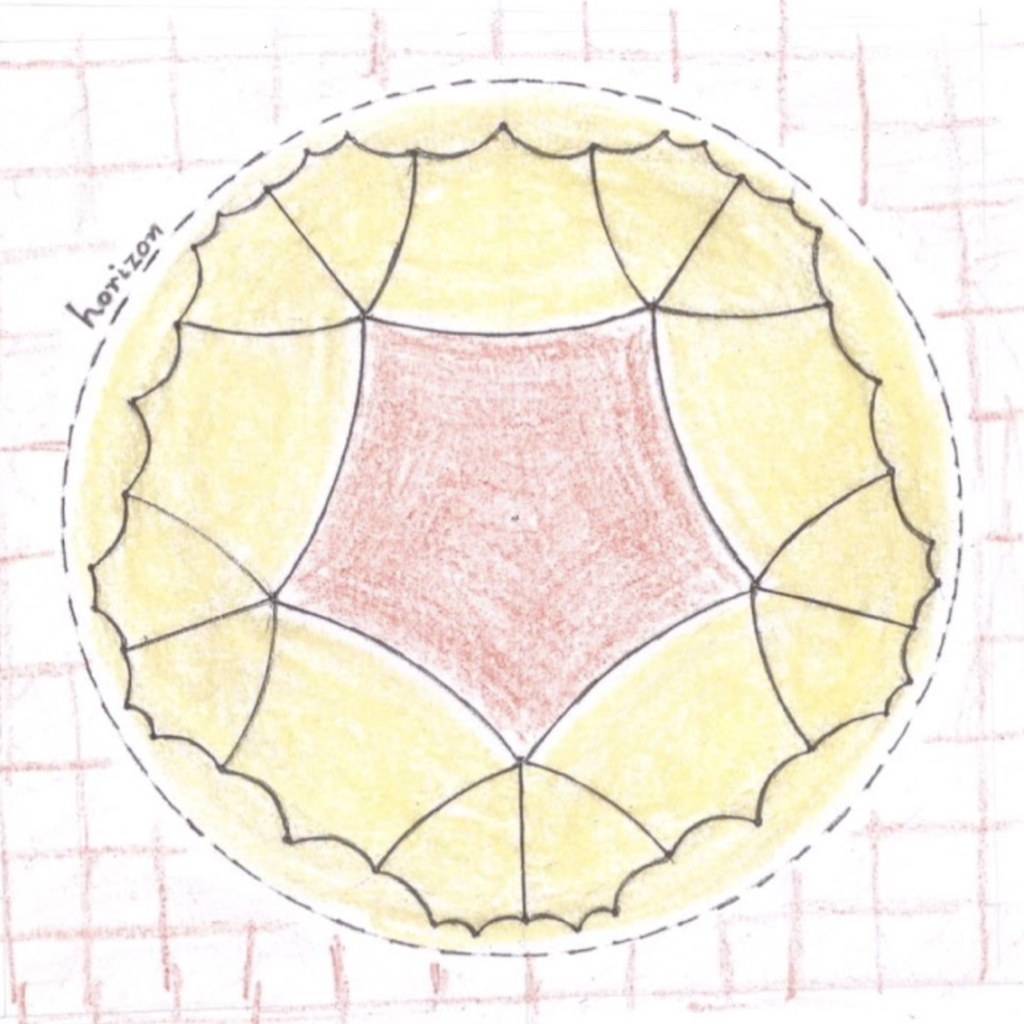The round yellow ` halo’, in which the red curved pentagon is inlaid, is such that its ` horizon’ cuts the edge-circles perpendicularly, so its size is ordained by the Pythagorean theorem: (\mathrm{radius\ of\ horizon})^2 + (\mathrm{radius\ of\ an\ edge})^2 = (\mathrm{distance\ from\ the\ centre\ to\ the\ centre\ of\ an\ edge})^2. Likewise, any regular genuinely curved polygon has a bounded—but limitless, the horizon is not assumed to be in it—halo, while that of an ordinary regular polygon shall be deemed to be the entire plane. The diagram on the left shows only the five primary reflections of the red pentagon in its edges, and two new reflections of each of these, but this suggests already that, the halo of any regular curved polygon is the union of its multiple reflections in edges! That these polygonal reflections are all in the halo, have circular edges perpendicular to the horizon, and the same angle at each vertex, is clear enough, because reflection in any edge keeps it fixed, preserves the perpendicular horizon as a whole, maps circles to circles, and preserves angles. However, as the diagram shows, these iterated reflections can contract in size very rapidly, so it is not obvious that any point P of the halo is in one of these reflections. To see that it is, we use the fact that the centres of the edges of all the reflections are outside the perpendicular horizon, so the radii of the edges which cut the segment joining the centre to P are all bigger than the positive distance from P to the horizon, so contraction in size is bounded for reflections in these particular edges, so only finitely many reflections are needed to cover this segment and find a polygonal reflection which contains P.
To make this result precise, we’ll now indulge in some “Grecian origami” involving these multiple reflections: we make a separate paper copy of each of these (infinitely many) polygonal reflections, and glue two of these paper polygons along an edge if and only if reflection in this edge switches their originals! This gives us a space locally like any closed surface, except possibly near the vertices v: we get a surface if and only if the angle of the regular curved polygon is a fractional number. For, a polygonal reflection incident to v returns to itself after some, say q, reflections in edges incident to v, only if the q-th, but no smaller, multiple of the angle is a multiple of 360 degrees, that is, the angle is 360r/q where the whole numbers r and q have no common factors. We dub this the Riemann surface of a regular curved polygon with p sides and angle 360r/q, and note that, it carries a tiling by infinitely many p-sided paper polygons q at each vertex; for example, all ordinary regular polygons have Riemann surfaces; and the one tiled by ordinary regular paper pentagons has ten at each vertex, because the angle is now 108 degrees, so r = 3 and q = 10. We examine next, the covering map f from the Riemann surface onto the halo, which identifies each paper polygon with its original. When r \geq 2, this map is obviously not one-one: the pre-image v of f(v) `branches off’ into r distinct pre-images when f(v) is varied slightly. That there is no branching when r = 1 is however not reason enough to conclude that the halo of a regular curved polygon with p sides and angle 360/q is tiled by its multiple reflections in edges. It is conceivable that f might fail to be one-one in a more subtle way: a sequence of edge-reflections covering a long loop, starting and ending at a point P of the halo, might bring us back to a different polygonal reflection containing P? The answer is `no’ because, the halo is simply connected—any loop at P can be shrunk continuously to the constant loop at P—from which fact it follows easily that f is a topological equivalence when r = 1.
Moreover, our tiling is `regular’ in its curved geometry: any vertex v of the red tile \mathbf{T} can be mapped to any other vertex w by a composition g of reflections in circles which preserves the tiling! Choose any sequence of tiles, starting with \mathbf{T}, and ending with a tile \mathbf{U} incident to w, such that each shares an edge with the preceding tile. From the way in which the tiling was defined, we know that the composition g of reflections in this sequence of shared edges maps \mathbf{T} onto \mathbf{U}, and by using preliminary reflections in the lines of symmetry of \mathbf{T} we can also ensure g(v) = w. Since g maps circles perpendicular to a circle C to ones perpendicular to g(C), we also know that, if P reflects in C to P', then g(P) shall reflect in g(C) to g(P'). So g maps the primary reflections of \mathbf{T} onto the corresponding primary reflections of \mathbf{U}, and likewise the secondary reflections of \mathbf{T} are mapped to those of \mathbf{U}, et cetera, so g preserves the tiling.
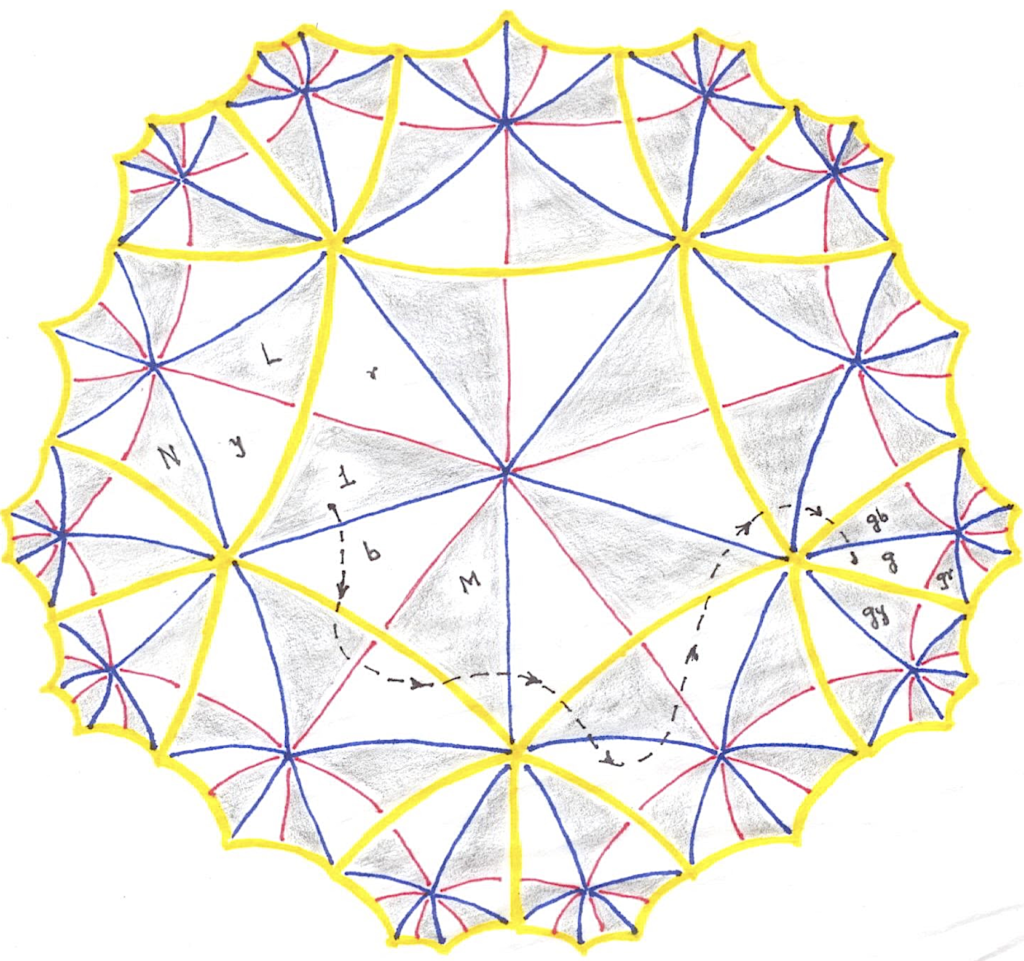
We’ll now subdivide the central tile by its lines of symmetry, extend this subdivision to all tiles by reflections in edges, and identify(!) each curved triangle with the unique symmetry g which maps any chosen basic triangle 1 to it. This subdivision is shown above for the pentagonal tiles of the last picture: their boundaries are in yellow, the new edges within them incident to their vertices are in blue, and the remaining edges are in red. So, the edges of any triangle have different colours, and symmetries preserve colours of edges. Using this we’ll now show that, the group of symmetries is generated by the reflections \{r, y, b\} in the edges of the basic triangle, i.e., any g is equal to a word in these three letters interpreted right to left as a composition of reflections.4 Indeed, r, y and b are the triangles sharing a red, yellow and blue edge with the triangle 1; so, the corresponding three triangles adjacent to any triangle h are hr, hy and hb; so, g is equal to the word whose letters give in succession the colours of the shared edges of any path of triangles from 1 to g; for example, the dotted path in the figure shows byrybybbrybybyb = g. Thus there are infinitely many ways of writing the same symmetry, for instance the identity 1, as such a word, but things are really not all that bad: any relation w = 1 can be reduced to 1 = 1 by using the obvious relations r^2 = 1, y^2 = 1, b^2 = 1, L^2 = 1, M^p = 1 and N^q = 1, where L = ry, M = br and N = yb This again uses the simple-connectivity of the halo: any loop of triangles can be built up from small loops enclosing at most one vertex of the triangular tiling, and the listed relations are easily seen to be all those that can arise from such small loops. The shaded triangles form the subgroup of all orientation-preserving symmetries—compositions of an even number of reflections—which is generated by any two of the three `rotations’ above, say L and N, subject only to the relations L^2 = 1, N^q = 1 and (LN)^p = 1.
The above groups are infinite, but this does not rule out that, by imposing additional relations, one can’t get, finite groups generated by two elements L and N whose orders (lowest powers equal to the identity) are 2 and q, while that of LN is p. Given such a group, we can double its size by a new generator y subject to y^2 = 1, r^2 = 1 and b^2 = 1, where r = Ly and b = yN, and then indulge again in some (purely topological) “Grecian origami” imitating the last picture: each element g of this doubled group is deemed a triangle with red-blue-yellow edges, and we glue the red edges of all the pairs \{g, gr\}, the blue of all pairs \{g, gb\}, and the yellow of all \{g, gy\}. The resulting space is a closed orientable surface—the boundary of a pretzel with holes—because each edge belongs to two triangles, each vertex to 2p, 2q or 4 triangles forming a loop around it, depending on whether the vertex is opposite a yellow, red or blue edge, and the shaded triangles of the initial group can be unambiguously deemed clockwise. Displayed in glorious yellow on the surface just described, we’ll plainly see finitely many p-sided topologist’s polygons, q at each vertex, and at the same time, displayed in fiery red, the dual topologist’s \{q,p\}! Moreover, the orientation-preserving symmetries of either give us back the initial group, and the cardinality of the doubled group gives, via an obvious Euler characteristic calculation5 the number of holes in the pretzel too!
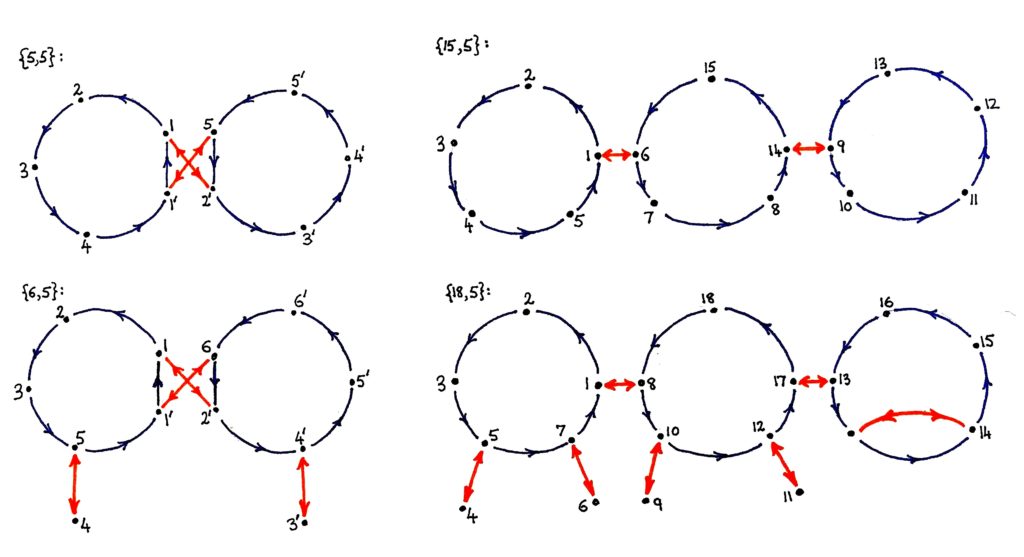
Finding such finite groups might appear formidable, but it is really a none-too-hard problem about something from school, viz., permutations, i.e., one-one functions of a finite set on itself. The job is only, to give, for each q \geq 3 and p \geq 3, permutations N of order q, and L of order 2, such that N followed by L is of order p, for the finiteness of the underlying set ensures that the generated group is finite! The figure above indicates one way of making these examples for q \geq 3 and p \geq q, which suffices because p and q can be interchanged. In each case, the finite set consists of dots and, the functions N and L are defined by the blue and orange arrows, respectively, dots without arrows being fixed points; and the numbering indicates the cycles of LN, i.e., N followed by L. In the upper left diagram, N has the two cycles of length q = 5, connected by an `orange cross,’ the two transpositions of L, and it turns out that LN has also two cycles of length q, viz., (12345) and (1'2'3'4'5'). There are q-2 fixed points of L in each, and by `dangling’ a new orange transposition to a new dot, as in the lower diagram, from the same number of these in the two cycles, we can increase the lengths of these cycles equally by this number, so this gives us the needed examples for q \geq 3, q \leq p \leq 2q-2. In the upper right diagram, N has t = 3 orbits of length q = 5 connected by the t-1 transpositions of L, and it turns out that LN is a cycle of size tq. By an orange double-arrow `shorting’ two consecutive fixed points of L on this cycle, or by up to q-1 danglers from them—the diagram on the bottom right has both!—-we can vary the size of this cycle from tq-1 (now LN also has a fixed point) through (t+1)q-1, which completes the job because any t \geq 2 can be used.
In fact, these non-Platonic `lost beauties’ exist in great profusion! For instance, we used two blue pentagonal cycles linked by an orange cross, but an arbitrarily long train of this type works too, so, there are infinitely many finite groups of type \{5,5\} (and the same is true for any non-Platonic pair)! Moreover, an orange cross within a single pentagonal blue cycle gives the smallest such group, which has 60 elements, namely, all the `even permutations’ of the five dots, so this particular \{5,5\} has t = 60 in the notation used in the section “Miss Universe”,6 so, twelve pentagons, five at each vertex, on a pretzel with four holes, and the bigger finite groups of this type will entail using pretzels with more and more holes! Most importantly, all these finite groups are obtainable by putting extra relations on the group of symmetries, of the tiling of its halo given by the multiple reflections of our red regular curved pentagon, for, we have proved that this infinite group has only the stated relations. So, if we are willing to think of these surfaces intrinsically, rather than being `of’ pretzels `in’ ordinary three-dimensional space, these infinitely many finite \{5,5\}s are all regular in the curved geometry they inherit naturally from that of the halo via these extra relations! Indeed, each of these relations is of the form g = 1, where g is a fixed point free composition of an even number of reflections in circles, and the surface in question is topologically equivalent to the space obtained by identifying all points of the halo which are related to each other by such g’s.
The regularity of the non-Platonic \{p,q\}s with respect to the curved geometry of the halo tells us that the parallel postulate must be invalid in it, and that is so: now lines are circular paths perpendicular to the horizon, and through a point not on a given line there are many non-intersecting lines! However, we still have a distance which is invariant under reflections in all lines, and Poincaré pointed out that it can be derived from the assumption that local measurements at ordinary distance r from the centre are made by using rulers which have shrunk(!) by the factor R^2 - r^2, where R is the radius of the halo. This is related to his rejection of the age-old notions of separate space and time in favour of a new principle of relativity to give Maxwell’s theory of light a coordinate-free meaning, for the distance we mentioned is just the right one if space-time is viewed projectively!
This last `lecture’ started with a pentagon and a pentagram, and has ended with their spatial analogues, but the game has barely begun! The dodecahedron is now almost crying out for its faces to be curved inwards, and starting with Poincaré himself, down to Thurston and others, magical things have been discovered thus; likewise, Gromov and others have lately been busy playing `dots-and-squares’ in halos; but here is where I’ll stop, except for the following tailpiece.
“bing’s ome”
One afternoon, I was telling someone with a math background how that little white “house with two rooms” and a sloping red roof—it was mentioned fleetingly in Part 1 of this article7—atop that roman aqueduct was, in fact, an example constructed by Bing of a space which is, contractible but not collapsible!
Its glass windows allow us to see that it is peculiar: one enters its rear room via a corridor attached by a flange to the front room, and vice versa! This is shown below in the line-drawing, more precisely, the position depicted is the one obtaining after the slightly overhanging roof has been `pushed in’ a wee bit to make it flush with the walls. There being no free edges left, we can’t collapse it any further. On the other hand, filling the house with sand, and then excavating out the same shows, just as plainly, that the 3-dimensional ball, which of course is collapsible, collapses also to Bing’s house!
At this point, I realised that I had not one, but three listeners, and that I had been talking above the heads, in more ways than one, of the other two! Two small girls, a precocious child of about ten, and her equally bright-eyed younger sister, who was probably still not of school-going age, were also with us (they and their parents were amongst a number of guests we had over for tea that day).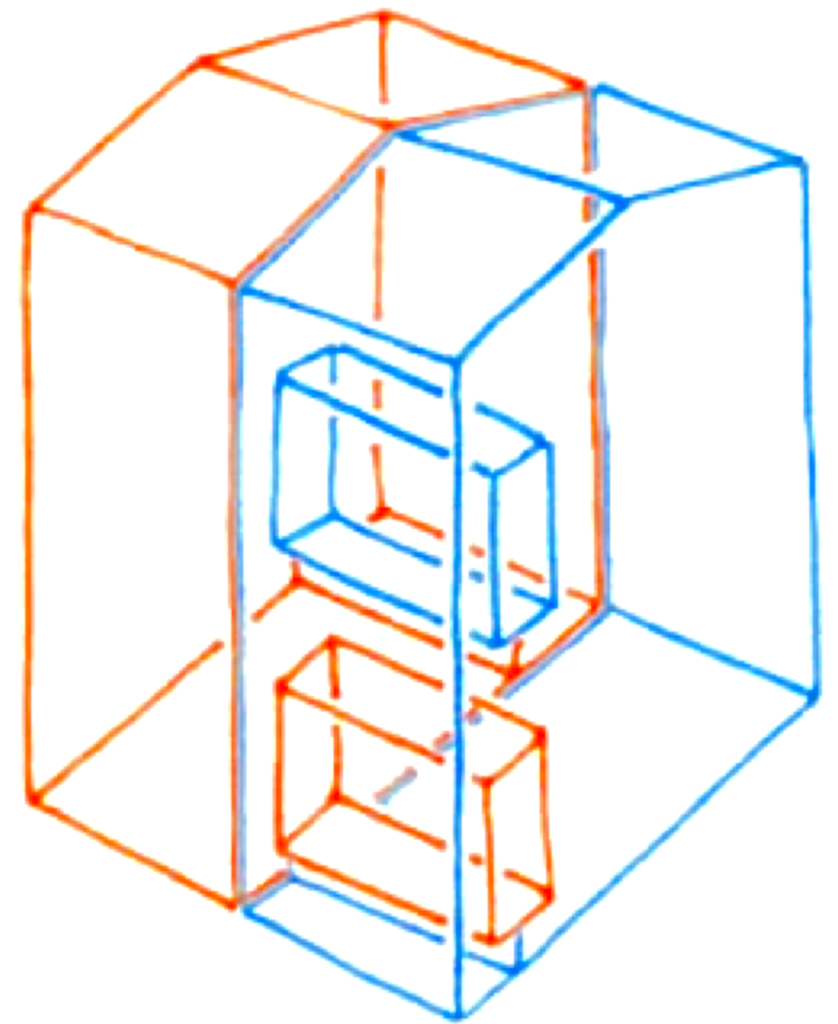 
To make amends, I switched to my story about that chotta aadmi [small man] who had, as a matter of fact, made this fully-functional paani ki taanki [overhead water tank], as well as this roman aqueduct with its thirteen (true) arches, all by himself, and who was, to tell the truth, still pretty much running the whole show, more or less… There was an indulgent and bemused look on the older child’s face as I spun out this yarn, but her little sister was impressed! She asked, “So he lives in the house with the two rooms, uncle?” “No, beta,” I replied, “that’s the pump-house. He lives, like all elves do, far far underground. That little cave in the wall, from where that tiny road comes out to that ramp leading to the spiral staircase winding around and up this taanki, and finally, that arch bridge to the aqueduct, I would suspect that that’s his route to and from work. But like most humans, I can’t see elves, so I’m not sure.” From the eagerness growing on the older sister’s face, it was clear that she had much surer knowledge than me, and sure enough, she soon took over from me entirely the further education of her sister on these rather technical matters pertaining to the habits of hobbits and elves and even ents! Her sister listened dutifully enough, but I couldn’t help noticing that she was, all the while, using her eyes, and so taking in the details on the rockery, more than her rather busy teacher. As the tiny stony brook hurtled down its rocks, and around that island with the tetrahedral agni mandir and the sacred peepul tree, into that water pond with “Beesmukhi” and its spout, and that double-curved bridge over it that takes one into the plant house.8
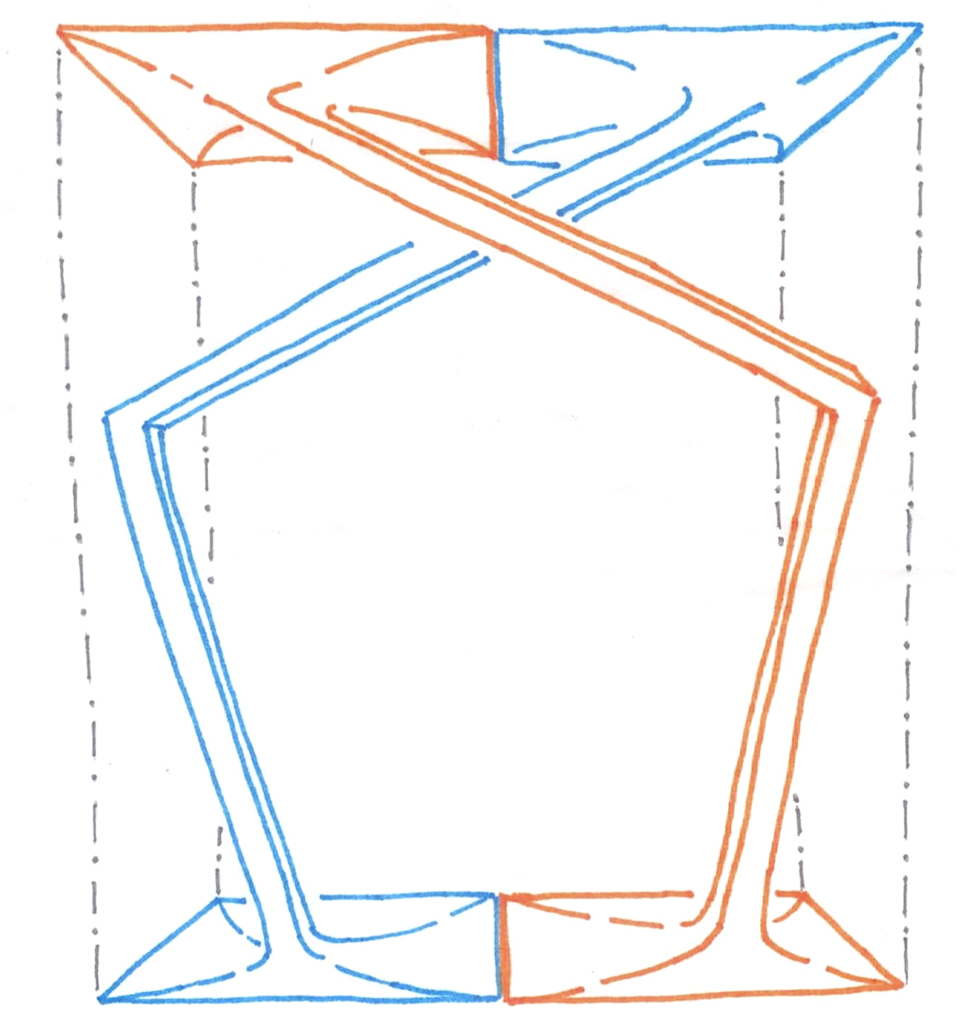
With the children busy in their play, the conversation returned to mathematics, and my companion now pointed out something which had been before my eyes all along, but which—duh!—I had not seen before: the mother golden-barrel in the background has its five prickly `pups’ arranged in pentagonal symmetry around it, just like that around each vertex of that icosahedron! In return, I explained why the above statue is called, “pi two is abelian!”. Minus the jargon, this basic theorem from topology says just this: any continuous mapping, of the top and bottom of the box shown in the line-diagram, which is defined in the same way on the two blue, and on the two orange squares, and which takes their boundaries to just one point, can be extended to a continuous mapping of the box which takes all its vertical faces to this point. To see this, extend in the obvious way to the two disjoint—but flared enormously near their ends—blue and orange square tubes, which join these pairs of squares, and map the rest of the box to the point!
By now we were sitting on the marble-quilted chabutra [platform] shown below, our legs dangling over the polished rounded edges of what had remained of the huge tile from which the halo of “Magic Carpet” had been cut, and were doing our maths on a yellow curved pentagonal table-top, made from the very piece that had been cut out from this halo to inlay its red counterpart! From this chabutra one can enjoy the passing show around and past both the entrances of the greenhouse, in particular, the cantilever roof above the main door9 is also visible, and my companion did not fail to notice that it was just like the top of “pi two is abelian!” This is so because this motif in concrete was originally intended to be done there on a bigger scale; likewise, something like the statue (p.33) near the other entrance to this plant-shed, which I, therefore, call “möbius’s balcony,” was once supposed to frame an intended balcony outside my office’s rear window! Since my companion already knew a simple10 method for making this one-sided surface—take a strip of paper, twist one end through 180 degrees, and glue to the other—there was nothing much I had to say about it.11 So, we just sat in silence, the better to enjoy another very pleasant and surprising feature of this place, which, frankly, was unintended too, it is pure serendipity: when the brook is flowing, there is almost as much sound of running water coming from the rear of this chabutra as from its front!
On our way out, we paused at the spot from where the sound of running water is transmitted via the metallic frame to the rear of the chabutra, to ponder the patterns made by fast-flowing water from the fall, over the pebbles of that gorge, as it about-turns into a subterranean tunnel and pool which feed the stony brook. It was about then that I told my companion, “That method of yours does not really give us a möbius strip of paper, indeed it can never be made, for, the material making it would prescribe an inner side, while we want a one-sided surface!” Now this is serious, not only am I faulting another method, it seems I didn’t come clean on mine either, but my companion saw the point I was trying to get across. Neither the concrete statue, nor the most delicate of models in the thinnest of papers shall give a möbius strip,for the simple reason that, it is an abstract idea: it exists in our imagination only: there alone is to be found that ethereal paper with zero thickness, the gossamer necessary to `make’ any mathematical surface. So, the “house with two rooms” atop the aqueduct, that too is not mathematician R.H. Bing’s example either, only an evocation of the same, and so on down the line, for all the motifs. They are all flawed depictions of flawless forms that can’t be seen as such—“like elves,” my companion teased me—but the fact that these imperfect depictions are so efficient in evoking in our minds these precise ideas, suggests that these `elves of mathematics’ are somewhat more important and natural, and in fact, most of these logical constructs arose historically from a contemplation of the patterns of nature. So it is not surprising that there is not only great beauty in these logically perfect thought-patterns12 of mathematics, they have also given us an ever-deeper understanding of nature’s patterns.
Conversation over tea that day had flowed smoothly on everything under the sun, but both were waning now, yet the older sister was chattering away with the grown-ups, but her sibling had left the skew room long ago. Fearing that she might be too near the water-pond in this fading light, I was relieved to find her by the aqueduct, but was taken aback by her posture: half-kneeling and stockstill, she was sort of squinting, steadily and fixedly, into that little cave! Setting myself down slowly on the grass beside her, I asked, “What is it, beta, what are you looking at?” Her voice was soft, but the two words were clear enough, and made my eyes dart to the “house with two rooms,” but it was not that, it was this cave only that was holding all her attention, as she repeated, “bing’s ome,” and moved a finger slowly towards it. The thought flashed that she was pulling my leg in return, but there was not a trace of naughtiness on that innocent face, and the thought was dismissed, as I looked at exactly where she was looking, but I saw only what you see in the photo above (which however was taken on a later day, in better light). While she remained in that fascinated state for about thirty seconds more, when, all of a sudden, her body relaxed and returned to normal, and it was clear that whatever she had seen, or thought she had seen, was no longer there. The happy smile the child smiled at me then presumed that I had also seen what she had seen, so I only smiled back. However later, on many evenings at about the same time, I have sat down on the same grass at the same place, and tried many contortions of face and squintings of eyes, hoping to espy, for myself, that elf which that little girl had apparently seen, but I would be lying if I were to tell you that I have seen it too, for I haven’t, not yet, anyways!
I remember reading that, try as they might, a small but significant percentage of people can’t see the hidden image in even the simplest of those “Magic Eye” pictures, so who knows, bing with a small `bee’ might be somewhere in the previous photograph, only you aren’t squinting at it properly? More seriously, I hope you managed to catch at least a glimpse of the shimmering beauty of the elves of mathematics, which indeed I have seen, and which I’ve tried to share with you, via these motifs, in this paper. \blacksquare
Footnotes
- See the third image on http://chdmuseum.gov.in/home/restshowcase/MTA=\#group-3. ↩
- Indeed, responding to Hilbert’s Third Problem, Dehn had shown in the year 1900 itself that the regular tetrahedron cannot be converted into a cube by any such sequence of moves!. ↩
- See p. 10–11 in “The Elves of Mathematics”. Bhāvanā. Jan 2020. 4(1). ↩
- See the section “Four half-turns” in Part 1 of this article, pp. 14–16 in “The Elves of Mathematics”. Bhāvanā. Jan 2020. 4(1). ↩
- See p. 10 in “The Elves of Mathematics”. Bhāvanā. Jan 2020. 4(1). ↩
- See p. 10 in “The Elves of Mathematics”. Bhāvanā. Jan 2020. 4(1). ↩
- See p. 13 in “The Elves of Mathematics”. Bhāvanā. Jan 2020. 4(1). ↩
- Tennyson’s “The Brook” is a favourite poem of mine since my early teens. ↩
- See p. 6 in “The Elves of Mathematics”. Bhāvanā. Jan 2020. 4(1). ↩
- Making the Möbius strip in concrete is however not as simple! I’ll like to express here and now my gratitude to Asa Ram, Miraj, Guni Laal, Ram Prakash, and all the other artisans who were involved in this work. Also, these motifs could not possibly have come into being without either the indulgence, or the organisational abilities of my wife, so here’s a very big “Thank you!” to you too, Minni! ↩
- Theorem : all equations which we solved in school using the quadratic formula, they form a Mōbius strip! For this see a later 2017 note of mine posted on kssarkaria.org/List.htm. ↩
- In the preceding `lectures’, I have used the motifs merely as gateways towards the much deeper beauty in these patterns of thought but, as I mentioned in the first part of this article, [See p. 13 in “The Elves of Mathematics”. Bhāvanā. Jan 2020. 4(1)] non-trivial effort is needed even to `see’ already-done mathematics. Therefore, to keep the focus on these very beautiful but demanding arguments, it was necessary to minimize all distraction; so only a bare amount of terminology was used, and just a few names were mentioned. ↩