
Jeffrey Renwick Weeks is most easily recognised as the author of the acclaimed popular math book, The Shape of Space, the third edition of which came out recently. Among mathematicians, he is also well-known for his contributions to hyperbolic geometry and knot theory, in particular for designing the software SnapPea, a widely used tool among low-dimensional topologists in the study of hyperbolic 3-manifolds.
From his days as a keen graduate student at Princeton learning the rudiments of geometric topology from Bill Thurston and his group, to his time as a MacArthur Fellow exploring the shape of the observable universe with a team of cosmologists, Jeff Weeks recalls his eventful career and his varied experiences as both a math educator and a mathematician in this engaging interview with Bhāvanā.
Follow Your Heart⁎
Jeffrey R. Weeks
When I first arrived in Princeton in 1978, I discovered that I was the only one in my entering class who hadn’t already taken graduate-level courses as an undergrad. Worse still, the Math Department, catering to its typical clientele, offered no introductory graduate courses. None at all. Our mandate was to learn–-or, for my classmates, review–-the basic stuff on our own, and then dive into the research-level courses that the various professors offered.
I was adrift. What should I have been doing? Studying even harder about Noetherian rings, the Radon–Nikodym theorem, etc. etc., all at a level of abstraction that I found neither useful nor interesting. What was my heart into? Learning some concrete geometry and topology, along with some general relativity. You can guess what I spent most of my time doing.
As you might imagine, my qualifying exams did not go well. On my first attempt, they let me off the hook on the basic topics with a humiliating but welcome remark that “you can learn this stuff when you teach it.” But for the advanced topics, they wanted me to try again the next year. They weren’t impressed then either, but they decided that I should start working on a thesis anyhow.
By then, I’d signed on with Bill Thurston as my advisor. I don’t remember what problems I was supposed to be working on, but I made no progress with them. What was my heart into? By that time, my fellow grad students, coloured chalk in hand, had introduced me to the beautiful world of low-dimensional topology, and I’d fallen in love with it. I’d also noticed that all books on the subject involved a lot of graduate-level algebra and analysis that really wasn’t needed to understand and appreciate the core concepts of geometric topology. So, I decided to ignore my thesis problems and instead took it upon myself to write the “missing book,” something that would welcome everyone–-from high school students on up–-into the magic world of multi-connected spaces.
That project took several years, with the book, The Shape of Space, finally completed in my fifth year as a grad student. My grad student stipend ended that year, so during what would have been my sixth year, I taught at Stockton State College and saved up enough money to return to Princeton and write a thesis in the seventh year. I don’t remember what I was supposed to be working on, but while Bill Thurston was away for the winter holidays, I decided to grant myself an indulgence to investigate some especially simple 3-manifolds and write a little computer program to find hyperbolic structures for some of them. I was lucky enough to stumble onto the smallest closed hyperbolic 3-manifold. During my first meeting with Bill after the holidays, I figured I’d briefly mention this little discovery. Bill responded with some ideas for how I might move forward with these investigations and how I might extend my little computer program. He said not a word about my old boring thesis topic, so by the time the hour was over, it was clear I had his blessing to do a thesis with my software for putting hyperbolic structures on 3-manifolds. “What my heart was into” had finally become “what I was supposed to be doing”!
Throughout six-and-a-half of my seven grad school years, I’d always felt that I would have been better off with a different advisor at a different school, with a firmer hand to guide me. But in retrospect, Thurston’s approach was exactly the right one: he let me find my own path. By the end of those seven years, I had some research software (SnapPea) and a book (The Shape of Space). In my heart, the book was my true dissertation. Even though it did nothing to satisfy Princeton’s Ph.D. requirements, it set the tone for my whole professional life, both in content (geometry, topology, cosmology) and in style (exposition for the general public).
As for my advice to current students, I dearly wish I could say “follow your heart” and leave it at that. But, of course, it’s not quite that simple. One needs a paying job. So, my advice is: follow your heart, and find a way to turn your passion into your livelihood. I wish you good courage and the best of luck.
A warm welcome on behalf of Bhāvanā! I must say I am really looking forward to our conversation. To begin with, we would like to hear about your childhood. Where did you do your schooling and what were your early interests growing up?
JW:Thanks! My dad was in the Navy, so every few years we moved from one place to another, sometimes on the U.S. East Coast, sometimes on the West Coast. I went to the regular state schools, where I especially enjoyed the science and math offerings. Outside of school, I liked the outdoors, first as part of the Boy Scouts and then hiking, camping and canoeing with my friends. I also liked to tinker with electronics, back in the “old days” when one could buy individual transistors, resistors and capacitors, and solder them together to make things.
Were you mathematically inclined right from your school days? Was there anyone from a mathematics background in your family or was there some teacher or mentor who influenced your interest in mathematics?
JW:I was mathematically inclined from the beginning, but during my school days, I never considered mathematics as a career. I expected to go into some sort of engineering or science, which of course is pretty close to math.
In a broad sense, how would you describe your learning years at school?
JW:Middle school was rough at times—at that age, the bullies tend to pick on the more intellectually inclined kids. But starting in 10th grade those problems went away, when the Navy stationed my dad in a new city, and I went to a new and larger high school where I found a wonderful group of intellectually inclined friends. Even outside of school we’d pass around books like The Strange Story of the Quantum (by Banesh Hoffmann), Mr. Tompkins in Wonderland (by George Gamow) and, of course, Flatland (by Edwin Abbott). Sometimes philosophy books too. In a way, these after-school conversations were a more authentic learning experience than what we were doing in class. Life was sweet.
On that same theme, my high school physics teacher took four of us “quicker kids” and told us not to come to physics class for the rest of the year, but instead, he told us to go to the library during that hour and learn physics with each other, using a book he gave us. It was a marvellous idea. Learning how to explore new ideas with each other was a vastly more useful experience than sitting in class. My teachers were all able teachers, but it was really the ideas circulating among my friends that were most formative. Indeed, exploring new ideas with one’s peers is a large part (perhaps the most important part) of what mathematicians, scientists and engineers do.
Indeed, I recall reading that you first fell in love with geometry in Grade 12 after reading Flatland, a book from 1884 quite ahead of its time. Did you chance upon this book or is there more to the story? What was it that fascinated you about Flatland?
JW:I just chanced upon it. It was one of the books getting passed around after school. Aside from its powerful use of the English language, the great thing about Flatland is how it encourages the reader to try to visualize four-dimensional space in his or her own mind. It drew me in, and for about two weeks I found myself trying to visualize a hypercube during every free moment, turning the idea over and over in my mind, trying to see it, but without success. Then, after about two weeks with this obsession, I finally “got it”. My joy at seeing that beautiful new world… words don’t suffice to describe what a pleasure it was. I was hooked. That’s really what drew me into mathematics, that there are these beautiful worlds out there, right at our fingertips, yet hidden from our view until we make the (often considerable) effort needed to see them.
How did your love of geometry grow from there extending to your undergraduate years at Dartmouth? I see that you studied both math and physics at Dartmouth.
JW:Yes, I bounced back and forth between math and physics. Which subject I planned to “major” in depended, I think, on how I was enjoying the courses that I happened to be taking in any given semester.
You eventually landed at Princeton, under William Thurston, no less. I would venture a guess that it was probably one of the most significant phases of your career. What were the circumstances leading to this? What made you choose math at this stage?
JW:I don’t remember exactly how I came to choose math rather than physics. It might have been the gradual realization that what I liked best about physics was the mathematics that’s baked into it, how beautiful mathematical models do such an effective job of describing the real world.

Even at Princeton, did you prefer Thurston naturally or were there other people and mathematical fields you had in mind? Was it gradual, was it some really interesting problem or graduate course that drove you towards geometry?
JW:There were no introductory graduate courses in the Princeton Math Department at the time, only research seminars (many years later I heard they’d changed that policy), but in the Physics Department, Barry Simon was offering an introductory course in algebraic topology. I took that course simply because it was the only graduate course I could understand. Barry Simon’s explanations were clear. That’s what got me started in topology. From there it was very gradual—I got to talking with some of Bill’s [Thurston] students, and then eventually signed on with him myself.
There must have been many pleasant memories of your time at Princeton and your time with Thurston.
JW:At that point, my contact was not so much with Bill Thurston himself, but with his other students. With many colour chalks in hand, they’d draw pictures of new and beautiful worlds. It was basically the same pleasure that I had once found reading Flatland, but now with an even richer variety of worlds to explore. So even though Thurston was available and helpful, my thanks go equally to my fellow graduate students.
Ah! I was coming to that. There have been quite a few accomplished students who worked with Thurston, some of whom would have been part of your peer group. Who were the other major mathematical influences in your time at Princeton, among peers and mentors? Could you dwell on any memorable moments that you cherish?

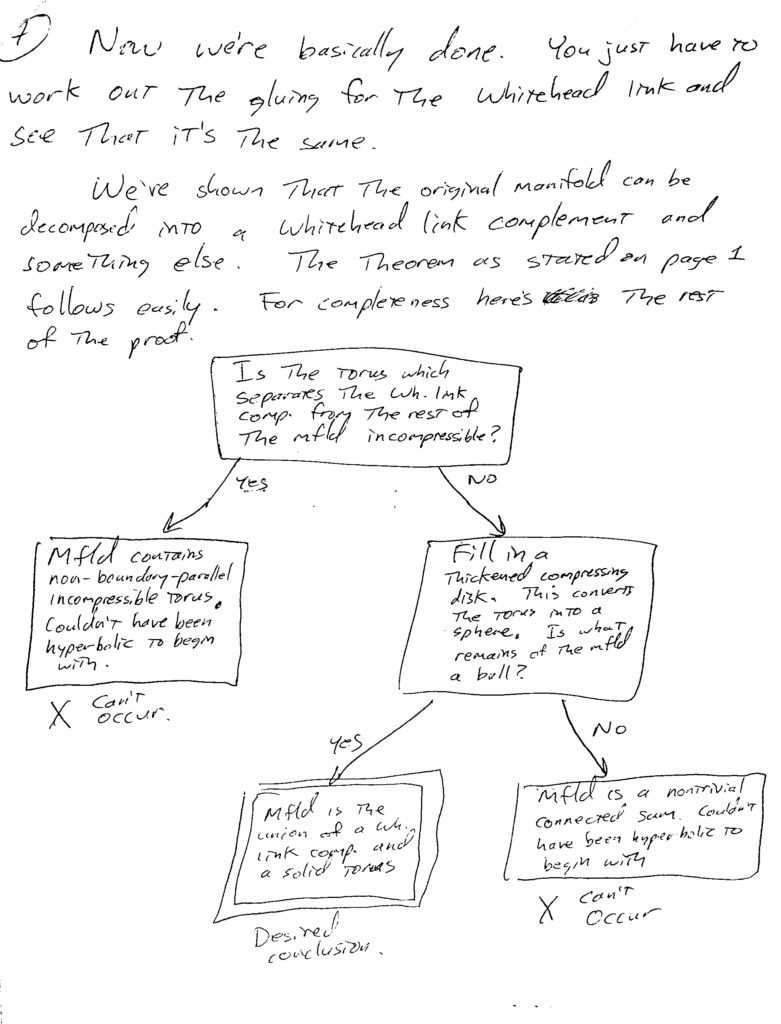
JW:Dave Gabai, Bob Meyerhoff, Bill Dunbar, Craig Hodgson, Silvio Levy, and others overlapped with me. My fondest memories are of standing in front of a chalkboard with them as they ever so patiently led me into those magical worlds. Things like, for example, how you can cut a solid torus out of a space and then reattach it differently.1 Finally grasping something so counterintuitive, yet ultimately so simple, was an exhilarating “Aha!” experience. Such moments are part of the joy of doing mathematics, for me and, I think, for most mathematicians.
And this visually stimulating, learning on the fly experience in your fledgling graduate days eventually ended up helping you, despite the initial hiccups.
JW:I was pretty much “lost in the wilderness” for most of my time as a graduate student. I arrived far less well-prepared than my peers (they’d all taken at least a few graduate courses as undergrads, I had not) and as I mentioned earlier, the Princeton Math Department offered no introductory graduate courses at all. We were supposed to learn it all on our own, if we didn’t already know it. I did my best, with mixed results. I also tried attending some of the advanced courses and seminars, but understood little.
Thurston let me chart my own course
The net result was that I was adrift, with some time on my hands. So I followed my true passion, which was writing an elementary book to bring some of those beautiful new worlds my friends had shown me, to a broader audience of non-mathematicians, including high school students. The result was The Shape of Space.
At the time, I considered The Shape of Space to be a sort of “guilty pleasure”, something I was working on when I really should have been working on a dissertation instead. Little did I know that it would set the tone for much of my professional life.
Thurston was awarded the Fields Medal in 1982, when you were working under him. What was your perception of him at the time? Did his working style have an influence on you?

JW:Bill Thurston left me free to do whatever I wanted. At the time, I felt he was an unlucky choice of advisor, that I would have done better with somebody who could have steered me along more systematically towards a dissertation. But I later realised that his approach was exactly what I needed: he let me chart my own course.
Thurston was reputed to have had a very unique visual style of thinking that made what seemed complicated to others, simple to him. Indeed he was as famous for his way of thinking as he was for his mathematical contributions with explanations that were known to be short and yet insightful. You have been privy to that remarkable prowess yourself.
JW:Yes. Thurston could, of course, produce very complicated and difficult proofs, that few others could even dream of finding. But what was even more striking was how he could see “simple” things—things that in principle any of us could have seen—but the rest of us never thought to look, and he did. He combined his formidable visualization skills with an almost superhuman ability to look at familiar situations in new ways.
Coming to your doctoral work, it seems to have led to quite a few interesting discoveries. Your primary focus was knot theory and hyperbolic structures on 3-manifolds. Did Thurston present you with this problem or was it completely your choice?
JW:Thurston had, of course, steered me in the general direction of knot theory and hyperbolic structures on 3-manifolds, but my specific dissertation project—writing software to compute those hyperbolic structures—was my own choice, chosen “on the sly”. I was in my sixth year of graduate school, and I was supposed to be working on something else. But while Thurston was away for the Christmas and New Year’s holidays, I decided to take a look at what sort of simple 3-manifolds I could construct. That’s when, among other things, I stumbled onto what turned out to be the smallest (and therefore simplest, in some sense) hyperbolic 3-manifold. After the holidays, when I met with Thurston to discuss whatever it was I was supposed to be working on, I started by mentioning the results of my little side project. He never explicitly said, “you should stop your other project and do this for your dissertation instead”, but as the conversation went on he mentioned various aspects of my side project that I might want to look into, and never said another word about my “main project”, so it was implicitly quite clear that he would be happy for the “side project” to become my dissertation. And it did.
Is that hyperbolic 3-manifold you refer to, the one named after you, the Weeks manifold–-independently discovered again by Fomenko and Matveev in 1988–-and which was proved to have the least volume of any closed orientable hyperbolic 3-manifold? What is a Weeks manifold, for the uninitiated?
JW:A 3-manifold is simply a three-dimensional space, typically one that wraps around and connects up with itself. Thurston’s big discovery was, roughly speaking, that every closed 3-manifold can be given a constant curvature geometry. The simplest and most symmetrical 3-manifolds admit spherical geometry, flat geometry, or one of five other possibilities.2 The generic 3-manifolds—the ones that aren’t so simple or symmetric—all admit hyperbolic geometry. So the Weeks manifold is, in a sense, the simplest of the 3-manifolds that aren’t simple.
I still like handwritten figures. The human touch lends them a special warmth
The SnapPea software was born out of your doctoral research. What was the thought process that went into designing such a software? I hear that it was actually meant to complement Thurston’s popular and widely circulated set of mimeographed notes on 3-manifolds from 1978–80.
JW:Thurston laid out the mathematics of finding hyperbolic structures on knot complements, and reshaping them to find hyperbolic structures on related closed manifolds (Dehn fillings). My thesis was an algorithmic implementation of his idea. Of course, Thurston’s 1978–80 notes contained lots of other stuff as well!
Your thesis had a lot of neatly handwritten diagrams. Thurston would have been very happy!
JW:With the wide availability of personal computers it’s now much easier to make precise computer-generated illustrations. Nevertheless, even now, I still like hand-drawn figures. The human touch gives them a special warmth.
What did you do immediately after graduating in 1985?
JW:I got a job teaching at Ithaca College and my wife got a job as a postdoc in biochemistry at Cornell, both in Ithaca, New York, USA. Two years later, we decided to have a child, and when our son was born I resigned my teaching position to be an at-home dad, an experience that leaves a new parent wonderfully happy yet thoroughly exhausted. During that period, I started collaborating with the newly founded Geometry Center at the University of Minnesota, working mostly during my son’s naps. I’d visit the Geometry Center for a week or so every now and then–-the Center had a lease on an apartment that short-term visitors could use–-but I never lived in Minneapolis on any longer-term basis. Instead I worked mostly as an external contractor. As the years went by I took on larger freelancing projects, at first with the Geometry Center and later with National Science Foundation support, and occasionally for science museums. Throughout those decades I always intended to return to a teaching position “as soon as I finish my current projects”, but as many of your readers know, one’s “current projects” are never finished—each project always rolls over into a new one.
You seem to be one among a rare breed of mathematicians, an unaffiliated freelancer with a strong research output. Given that you were out of the usual academic circuit and the sometimes stressful obligations that come with it, was there greater freedom in defining and pursuing research interests that were close to your heart?

JW:Yes and no. For sure it’s been a big plus having minimal administrative responsibilities, and not having to attend committee meetings. On the other hand, with no regular salary, I’ve always needed to find external funding for my projects. All in all, I’ve been lucky in being able to work on the projects closest to my heart.
Of course you did some considerable work in hyperbolic geometry and knot theory after graduating from Princeton, notably in your collaborations with Colin Adams, and also with Carlo Petronio and Makoto Sukama.
JW:I first met Carlo Petronio when I was going to Italy anyhow (my wife is of Italian origin) and I took a side trip to Pisa to see Carlo. With Makoto Sakuma it was the opposite: he happened to see one of my papers just before he left on a trip to Toronto, and asked whether he could take a side trip to come visit me in Middlebury, Vermont, where my family and I were living at the time.
I don’t remember when Colin Adams and I met—it feels like we’ve known each other forever—but it was natural for us to be in touch because we’d done some very similar work with hyperbolic structures on knot complements. You might be amused to know that Colin and I wrote letters on pieces of paper, which we physically mailed back and forth. We used coloured pens to make the diagrams.
I see! Like you, Adams himself is known for his simple explanations of quite advanced topics. And then, of course, there was the MacArthur Grant in 1999. Was that unexpected?
JW:Completely. The phone rang, and the Director of the MacArthur Foundation introduced himself. He asked me whether I’d heard of the MacArthur Fellowships. My mind was racing ahead, but I couldn’t let myself even think that he might be offering me one until he said it first. I then had to keep it secret for a week, although I requested—and was granted—permission to tell my wife and son.
Your time as a MacArthur fellow is prominent given that it also coincided with the period you were working on questions in cosmology, primarily concerning the global topology of the universe we live in. You worked with the likes of Jean-Pierre Luminet in analyzing NASA’s WMAP (Wilkinson Microwave Anisotropy Probe) data concerning the Cosmic Microwave Background radiation. How did this shift to cosmology transpire? You were, in fact, working along those lines prior to the award of the grant, having published results to that end in 1998.
JW:At some point in the late 1990s I got an email from Neil Cornish, an astrophysicist I didn’t know at the time, asking whether I knew the so-called “eigenmodes of the Laplace operator” for some class of 3-manifolds. I didn’t, but I gave him the name and address of a mathematician who did. Then I asked Neil, just out of curiosity, why he was interested. Neil explained that he and his colleagues David Spergel and Glenn Starkman were hoping to use the Cosmic Microwave Background (CMB) radiation to test whether the universe is finite, and if so, to determine its topology. You can imagine how I lit up! Determining the topology of the universe was a dream I’d had ever since I was first writing The Shape of Space, but I’d never thought that this dream might be realizable in my lifetime. I eagerly signed on as a collaborator of Cornish, Spergel and Starkman, and later of the French cosmologists Luminet, Roland Lehoucq and Jean-Philippe Uzan as well. In effect, I served as their “house geometer”, providing geometrical and topological help in support of their cosmological research.
Did your physics background suffice for this work? Or did you have to traverse a rapid learning curve?

JW:I got lucky. Twenty years earlier, while I had been “lost in the wilderness” during my first year of graduate school, I decided to learn some general relativity, just for fun. (An aside: Misner, Thorne and Wheeler’s book Gravitation, in spite of its massive size, is one of the most accessible math/physics books I’ve ever read. It’s full of pictures!) During those same years, I also applied Einstein’s equations for gravity to an expanding universe in each of Thurston’s eight curved geometries, and ran some simulations. This “random chance” tinkering with cosmological models turned out to be just the background I’d need 20 years later to effectively collaborate with cosmologists.
I presume you were the only mathematician among a team of (French) cosmologists. So did they just leave you to do the math while they worked out the physics?

JW:No, the collaboration was far more interactive than that. Cosmologists know an impressive amount of math. We speak the same language. (I mean the same scientific language. As for the human language, with the French group, we’d sometimes work in English, sometimes in French. The scientific vocabulary is pretty similar.)
We spent a lot of time doing things like figuring out the “harmonics” of spaces with various geometries and topologies, which are needed to adapt the standard cosmological model to a multi-connected space. With the harmonics in hand, one can get a prediction of what the CMB should look like in such a space. The exact pattern one sees on the sky also involves a “roll of the quantum mechanical dice”, so the prediction isn’t an exact pattern, but merely a probability distribution for what one would expect to see. Nevertheless, such probability distributions can be compared to WMAP’s observations. Ultimately, one favours spaces for which the observed sky is “typical” for a given space, and rejects spaces for which the observed sky would be highly unusual for that space. We found a few of the former, and plenty of the latter!
Eventually, the model proposed was the Poincaré dodecahedral model, a finite state of affairs. That would have been a very surprising thing! What was the reaction like? What’s the status on the veracity of that model at the moment?

JW:As it turned out, another group had searched for “matching circles in the sky” that could have detected a universe like the Poincaré dodecahedral space, but failed to find them. They hadn’t yet released those results, though, and we were unaware of them. So the reaction to the dodecahedral space model was less than enthusiastic. A third group later claimed that the various sources of noise in the CMB would be sufficient to hide such matching circles. The question of the noise levels became moot a few years later when the Planck satellite found the observable universe to be flat to within a much tighter tolerance. A flatter observable universe means that if the universe as a whole were a Poincaré dodecahedral space, we’d be seeing only a very small part of it, too small to create the matching circles effect. More fundamentally, that would also mean that such a dodecahedral-space universe would be too big to explain the empirically observed anomalies in the CMB that led us to that model in the first place. In other words, the Poincaré dodecahedral space model remains consistent with all observations, but at such a large scale that there’s no reason to prefer it over any other topology.
You delivered an invited talk at Princeton as part of the 2007 conference “Geometry and the Imagination” held in honour of Thurston’s 60th birthday. Did you maintain a regular correspondence with Thurston all the time after your graduate days? Did you two ever collaborate after you left Princeton?
JW:We used to exchange an occasional e-mail. Our last correspondence was in 2010, when we were discussing the design of some topology construction toys (“zippergons”) that Bill was making from sheets of craft foam, and had me test for him. But we never co-authored any more papers.
Your expository paper “The Poincaré Dodecahedral Space and the Mystery of the Missing Fluctuations” (Notices of the AMS, 2004), won the Levi Conant prize in 2007, a prize meant for outstanding expository papers. Going by your other articles and lectures too, you evidently possess a knack for effortless exposition yourself. Was it something you cultivated consciously or did it come to you naturally?
JW:I love exposition—especially for the general public—but “effortless” it is not. The pleasure in doing it comes naturally, but even when lecturing on a familiar topic for the twentieth time, I still need to devote many hours to prepare, including two or three practice runs at home to get everything fresh in my mind and get the flow right. It’s a bit paradoxical, but obsessive preparation gives one the freedom to be spontaneous on stage.
That is actually a great piece of advice for any aspiring teacher. On the same note, your book The Shape of Space is probably one of the most recommended books for anyone remotely interested in topology and admired by mathematicians and the uninitiated alike. Could you give us some background on your writing experiences? How did it all come about?

JW:At the end of class one day, one of my undergraduate professors showed us a two-sided Möbius strip. I thought that was really cool, and went to my advisor to ask about the possibility of doing a senior project in topology. My advisor kindly pulled an introductory topology book off his shelf and loaned it to me. Alas like most (all?) topology books of the day, it was cold and formal, eschewing pictures and instead, taking the set-theoretic approach of defining a “topology” to be a collection of open sets satisfying blah, blah, blah. All the fun of topology had been lost.
At Princeton a few years later, my fellow graduate students and Bill Thurston, coloured chalk in hand, introduced me to an even richer topological world. Like that two-sided Möbius strip,3 it was all so accessible. Anybody who cared to make the effort could understand that beautiful world from the pictures alone, with no need for the heavy formalism found in graduate school textbooks (well, unless one wants to do research in the field). But there was still no accessible broad-audience book. So I decided to write the book that I’d failed to find for myself when I was a student. My goal was to write a book that my high-school friends and I might have passed around along with Mr. Tompkins in Wonderland and Flatland.
What about your involvement in mathematics education? Did Thurston have any influence on your involvement in that field?
JW:No. Not in any major way. We did, though, co-author a Scientific American article.4 And I suppose his interest in math education might have increased his tolerance for my taking so much time to write The Shape of Space.
Obsessive preparation gives one the freedom to be spontaneous on stage
Since you mentioned your time at the Geometry Center earlier: I remember reading about an innovative hands-on geometry workshop offered by Thurston, John Conway, Peter Doyle and Jane Gilman for an eclectic mix of high school students, college and high school teachers, and math undergraduates. It was titled Geometry and the Imagination. The prescribed reading book for that course was The Shape of Space. Were you involved in that too?
JW:I was not involved in the Geometry and the Imagination course, although, as you say, the book was.
I have noticed a lot of your delivered talks are welcoming to audiences of all ages and backgrounds, although they deal with advanced mathematical concepts and themes. What’s the preparation process like?
JW:When preparing a talk, my first step is to decide what the main point is, and then to ruthlessly strip away everything inessential to that one point. One beautiful idea per talk is enough! My second (and even more important) step is to think very carefully about the likely audience: what will their backgrounds be? What will they already know or not know? I then try to start every talk with something that every person in the audience will be comfortable with. After about five minutes of that, I start taking the first baby steps towards whatever that day’s goal is. The key, I think, is to lead the audience along a path towards the main goal in a systematic way, one small step at a time.
That tip should come in handy! You have also given popular lectures on visualizing 4D space for the general public. Do you employ the same idea as in the 4D maze game where the extra dimension is given a colour attribute?
JW:Yes, I like the approach of letting colour represent the fourth dimension.
The alternative would be to use some sort of 3D projection of a 4D object—for example, the cube-within-a-cube drawing of a hypercube. The advantage of such a projection is that it’s relatively easy to explain to people; if you had only two minutes to show somebody a picture of a hypercube, this would be the way to go. The disadvantage of such a projection is that when you look at it you’re making no progress towards true 4D visualization.

That’s why I like the colour-coding. It takes a little more effort to get started with, but the payoff is that as you get more and more comfortable with the colour coding, it offers a natural transition to true 4D visualization. What do I mean by “true 4D visualization”? In effect, you stop drawing the colours and instead just “sense” how far each point sits in the fourth dimension, in much the same way as you can close one eye, look around a room and just “sense” how deep each object sits in the scene, even though the 2D image on your retina lacks that information.
Coming back to SnapPea, it is perhaps a one-of-a-kind software that has aided mathematical visualisation and is tied very concretely to research in a field as advanced as low-dimensional topology, particularly hyperbolic 3-manifolds. For instance, along with Patrick J. Callahan and Martin Hildebrand, you worked on a census of cusped hyperbolic 3-manifolds essentially aided by SnapPea and there have been many more such studies since then. Are you still actively involved in improving SnapPea? Also, how do you foresee the ubiquity of such software in the future, as a support system to research in such abstract mathematical areas?
JW:About a decade ago I was getting seriously overwhelmed, trying to keep SnapPea up-to-date while simultaneously developing and maintaining geometry and topology software for the general public. So with SnapPea, I passed the baton to Nathan Dunfield, Marc Culler and Matthias Görner, who are doing a spectacularly good job keeping it healthy and moving it forward—far better than I would have done.
As for your second question, not only in the future, but already in the present, I think SnapPea and similar software have already proved to be ubiquitous among researchers in these specialized fields.
Sticking with SnapPea, you initially developed the program using C, although there is now a Python version, SnapPy, developed by Nathan Dunfield, Marc Culler and Matthias Görner. Is C still your language of choice while developing any such software or are you moving towards Python?
JW:I still prefer C for the mathematical heart of each app, because it’s so wonderfully portable. User interface languages vary by platform—C++ on Windows, Java on Android and now Swift on iOS/macOS—but they all call the same C code to do the math. C’s runtime efficiency is also appealing.

On a related note, you have also striven to incorporate an innovative method of virtual visualization as a teaching aid by way of computer games. I have played some of them on the website (www.geometrygames.org) you maintain such as tic-tac-toe on a Klein Bottle, chess on a torus, the 4D maze, etc, and they are all immensely enjoyable. It goes without saying that tools like these would go a long way in making mathematical learning and education a pleasurable activity and also in building intuition. I presume that was part of your objective too while developing these games. How has your experience been in this context?
JW:Indeed, that was my main objective, to help bring topology and geometry to the general public, for example by “putting a flat torus in the palm of the player’s hand”, or “putting a wallpaper symmetry group in an artist’s hand”, and so on. In practice, it’s worked out well. Even small children catch on quickly. In fact, I think small children catch on to the idea of a flat torus more quickly than their parents do, because children have fewer preconceptions and less trouble letting go of them.
Do you have any interests not connected to math?
JW:My main recreational interests are outdoors. After work each day, my wife and I go out for about an hour, either on bicycles in the summer, on cross-country skis in the winter, or running in the mid-seasons (but for only half an hour when running). It may sound counter-intuitive, but I find intense exercise physically relaxing and also mentally relaxing.
My other hobby is foreign languages. If I visit another country, for about a year ahead of time I’ll spend about half an hour each evening trying to learn a little bit of their spoken language, so I can talk with people (if only at a very basic level) when I get there.
You must have learnt quite a few languages then! One final question. What are you working on presently?
JW:In the U.S. I would say a “pool game”, but in India, I guess you would call it a “billiards game” instead. So, a non-Euclidean billiards game in virtual reality, which lets players put on a VR [virtual reality] headset and experience three-dimensional hyperbolic space, Euclidean space, or a hypersphere directly.
Sounds like an exciting project to look forward to for all of us! It has been a real pleasure to talk to you and we are really grateful to you for taking time out of a busy schedule for this wonderful conversation.
JW:The pleasure was mine. Thank you!\blacksquare
Footnotes
- This article was originally published by Jeffrey Weeks, edited by Allison Henrich, on the blog Living Proof of the American Mathematical Society. It is republished here, with minor edits, with permission from the author, the editor and AMS.↩
- Editor’s note: Chapter 9 of Dale Rolfsen’s book Knots and Links explains Dehn surgery. The article “Computation of Hyperbolic Structures in Knot Theory” by Jeff Weeks in The Handbook of Knot Theory explains the hyperbolic aspects of the same. ↩
- For details, please see Chapter 18 of The Shape of Space. ↩
- Chapter 8 of The Shape of Space explains two-sided Möbius strips. ↩
- Jeffrey R. Weeks and William P. Thurston. “The Mathematics of Three-Dimensional Manifolds”. Scientific American. 251(1): 108–120 (July 1984). ↩
