 |
 |
This article, offered as a tribute to the two towering figures in the Indian milieu, is in three parts. The first part is a biographical sketch of NRS by Rajinder Singh, the second part on VVN is by A.R. Prasanna, and the third part by Jayant V. Narlikar is a graphic exposition of the significant contributions of NRS and VVN to general relativity, specially around the Kolkata and Banaras schools that flourished under their fostering mentorships.
Nikhil Ranjan Sen (1894–1963)
By Rajinder Singh
Nikhil Ranjan Sen (also written as Nikhilranjan Sen) was a leading figure in the early development of research on the theory of relativity in India. His research work mainly focussed on topics such as the theory of relativity, cosmology, fluid dynamics, ballistics, quantum mechanics and wave mechanics – all relating to aspects concerning applications of mathematics – that justly earned him the epithet of the father of applied mathematics in India. He was associated with various institutions such as the University of Calcutta, the Indian Statistical Institute, the Calcutta Mathematical Society, and the Indian National Science Academy. The present tribute offered here, honouring his significant contributions, is based on the book N.R. Sen – His Life and Scientific Work [1] and presents a brief summary of his life and of his scientific work.
Early life and education
Born on 23 May 1894 in Dhaka, Nikhilranjan Sen was the youngest of four sons and four daughters of Kalimohan Sen and Vidhumukhi Devi.
A tradition of pursuing mathematics ran in the family. Though a lawyer by profession, his father Kalimohan Sen passed the BA examination in Mathematics in 1877, securing first division from Presidency College, Calcutta. Kalimohan’s younger brother Rajmohan Sen was a reputed teacher of mathematics, a professor at Rajshahi College (now in Bangladesh) and later became the Principal of the college. Rajmohan’s son Bhupati Mohan Sen studied mathematics at the Presidency College, did his MA from Cambridge University, and obtained the distinction of being a Senior Wrangler.1 He was also the first Indian to receive the Smith’s prize.2
Beginning his early education at the Dhaka Collegiate School, where one of his classmates was the celebrated physicist Meghnad Saha, Nikhilranjan later studied at the Rajshahi Collegiate School – both these institutions are located in today’s Bangladesh. In 1909, he appeared for the entrance examination of the University of Calcutta, and stood third in the order of merit to obtain a scholarship. Passing the intermediate examination in 1911, he did honours in mathematics from Presidency College in Calcutta, where Saha and Satyendranath Bose were his close contemporaries, and Jagadish Chandra Bose was their teacher. Finishing his honours in 1913, Nikhilranjan went on to do post-graduation in mixed mathematics at the same college, and stood first in the 1916 MSc examination.
Starting his teaching career soon thereafter, he worked first as a Research Scholar, and then as Lecturer in the Applied Mathematics department at the University College of Science in erstwhile Calcutta for four years. At the same time, he continued his research studies as well, and wrote some important papers.

The Newtonian potential is a central concept in potential theory. N.R. Sen published an article in 1918, titled “On the Potentials of Uniform and Heterogeneous Elliptic Cylinders at an External Point” in the Bulletin of the Calcutta Mathematical Society [2]. A year later, the same article was [re]published in the British journal Philosophical Magazine [3]. In this work, NRS introduced an integral method to express the potential of an infinite elliptic cylinder as a trigonometric series, applicable in certain cases of heterogeneity. Additionally, in his article [4] titled “On the Potentials of Heterogeneous Incomplete Ellipsoids and Elliptic Discs”, published in two different journals, NRS applied the method of discontinuous integrals to solve the problem of determining the potentials for both heterogeneous incomplete ellipsoids and elliptic discs.
Based on this research, he submitted his DSc3 thesis in 1921, with an incomplete looking title. As per the statutes of the university, three faculty members had to give testimonials in his support, and it was referred to Gilbert T. Walker, D.N. Mallik, and Asutosh Mookerjee. Expressing the opinion that the thesis is worthy of being awarded the degree, their brief evaluation report4 wrote: “We have seen that his thesis was based on different published articles. This seems to be the reason that the title of the thesis, according to the official record was Potentials of Uniform etc.”
The degree award resulted in NRS being appointed Ghosh Professor. He was sanctioned an allowance of Rs. 500 per month with effect from 1 September 1922, which enabled him to carry special research in Europe.5 Soon after this, he went to Germany to pursue his PhD.
NRS was well-versed in both the theoretical and experimental work being done in India before arriving in Germany, where it would become the focus of his PhD thesis. In Germany, NRS began his research under Arnold Sommerfeld at the University of Munich. After just about a year, for reasons that are not well-documented, he moved to Berlin to work with Max von Laue at Humboldt University. There, he wrote his thesis titled “Über die Grenzbedingungen des Schwerefeldes an Unstetigkeitsflächen” (On the Boundary Conditions for the Gravitational Field Equations on Surfaces of Discontinuity), which was published in the reputed German journal Annalen der Physik [5].
Contribution to theory of relativity

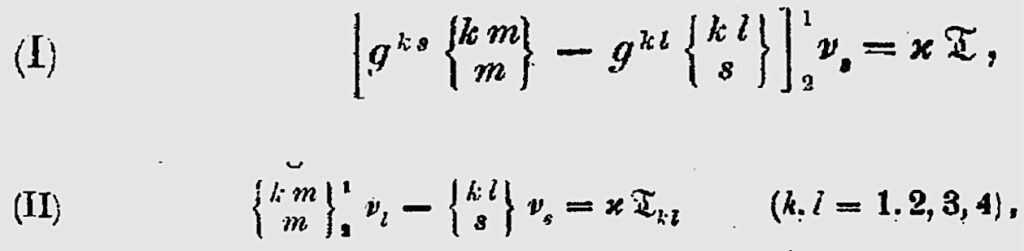
In his PhD thesis, among the many things he accomplished, he proved that adding the cosmological constant to the gravitational equations does not change equations (I) and (II).

During his stay in Germany, NRS wrote two papers with his guide von Laue dealing with de Sitter’s world [9] and [10], and change in potential of ions and emitted electrons of glowing metals.
After completing his PhD, NRS returned to India and resumed his role as a professor in the Department of Applied Mathematics at the University College of Science. There, he continued his extensive research on various aspects of the theory of relativity.
Cosmological Universe models and NRS’s views
In 1917, Einstein proposed a statistical model of the Universe, characterized by a cylindrical shape, isotropy, and homogeneity. To account for the repulsive interaction between bodies within his field equations of general relativity, he introduced the cosmological constant. However, Einstein’s model lacked experimental evidence. In response, Willem de Sitter from Holland suggested an alternative model where the universe is spatially flat and devoid of ordinary matter. In the de Sitter model, the dynamics of the universe was governed by Einstein’s cosmological constant \lambda, which determined the rate of expansion. Von Laue and NRS explained de Sitter’s universe by considering the cosmological constant, and showed that by transforming the field inside a spherical shell with a surface distribution of matter, it could resemble de Sitter’s universe, which could then be derived as a limiting case from the shell’s gravitational field.
In the late 1920s and early 1930s, Edwin Hubble and his colleagues in the United States demonstrated that, beyond the Milky Way, other galaxies were moving away from us. This provided experimental evidence for the expanding universe. The question, then, was to explain the universe’s expansion. Arthur S. Eddington proposed a model, which was based on condensation. In 1933, NRS, in his article [6] titled “On Eddington’s Problem of the Expansion of the Universe by Condensation”, demonstrated that the expansion of the Einstein universe would begin regardless of the number of condensations. He concluded that the number of condensations did not affect the expansion process. Additionally, NRS found that the model was unstable with respect to symmetrical mass condensation.
In his subsequent work, NRS explored how pressure affects stability. He showed that stability could either be restored or exacerbated depending on the pressure distribution within the system. Although he mistakenly used a four-dimensional volume element in his calculations, improved results were later presented in his paper [7] titled “On the Stability of Cosmological Models with Non-Vanishing Pressure”.
In 1932, E.A. Milne introduced a theory using static space-time metrics that did not assume a homogeneous matter distribution or account for gravitational interactions. He suggested that the universe’s density changes due to an initial explosion of matter. His model deviates from general relativity’s predictions on space curvature caused by matter distribution until the universe’s density reaches zero. NRS and N.K. Chatterjee examined the equilibrium of polytropic gaseous spheres in the context of Milne’s theory, focusing on two astrophysically relevant cases, and found that the central density remained very high, even within the degenerate core of Milne’s model. In 1936, NRS authored a comprehensive article on Milne’s model. In this work, he stated that, at every point in space and at every moment in time, there are rapidly moving material particles with velocities approaching the speed of light.
Structure of stars
Galaxies have millions of stars. The question was about the structure of the stars. From 1920s onwards various theories were proposed by different scientists like Ralph H. Fowler, Edmund C. Stoner and Subrahmanyan Chandrasekhar. Milne’s student Thomas G. Cowling proposed “a point source model”, in which the whole energy of a star was generated at the centre, whereas the opacity and mean molecular weight of gas were assumed to be constant. In 1937, NRS showed that classical mechanical equilibrium equations were inadequate for dense, degenerate sphere cores following Stoner’s pressure-density relation. He recommended using Einsteinian mechanics instead, noting that, at high densities, the sphere size predicted by Einsteinian mechanics is significantly smaller compared to classical mechanics.
NRS published a study on density gradient inversion and convection in stellar bodies in 1941 in which he proposed a model where a star has a convective core at its centre, characterized by an adiabatic gradient, that allows for the mixing of matter with an adjacent radiative envelope. He emphasized the importance of the Cowling model, in conjunction with Bethe’s energy generation theory, which requires a stellar model with convective radiation. This model helps estimate hydrogen content in low-mass stars. NRS and his team created a convective-radiative stellar model applicable to specific densities. Their results aligned with solar values and showed that integrating the Cowling model with Bethe’s theory provides a satisfactory model for stars like the Sun. In their next publication, they included helium in their calculations and found that accounting for helium eliminated the small discrepancies between the observed and calculated stellar radii from their previous work.
In astronomical theories, stellar bodies are frequently considered as hot gas masses in equilibrium. NRS studied Emden’s theorem on the expansion or contraction of a polytropic gas mass with a constant index. He derived an equation to estimate the temperature distribution in a variable polytrope, using its maximum and minimum polytropic indices.
In 1954, NRS and T.C. Roy developed an analytical method for accurately modelling red giant stars that avoided singularities, and aligned with the expanding universe model without relying on Einstein’s equations. Their approach, based on Newtonian approximations, demonstrated that at astronomical velocities, the gravitational mass and rest mass of a cluster are nearly identical, thus confirming classical Newtonian dynamics. They also found that as a cluster contracts, its gravitational mass decreases by about five percent from its rest mass, and identified a minimum radius for a given rest mass.
Fluid dynamics
NRS investigated a broad array of topics, including celestial objects such as stars and nebulae, as well as hydrodynamics, with a special focus on contemporary theories of turbulence.
On his deathbed, German physicist Werner Heisenberg remarked that the two greatest unresolved challenges were reconciling quantum mechanics with general relativity and understanding turbulence.
In 1924, still a young scientist, NRS taught postgraduate courses on the theory of elasticity, hydrodynamics, and solid geometry at the University of Calcutta. While teaching, he identified unresolved problems, one of which he explored in his paper on long waves in canals with varying sections. He focused on solutions by adjusting functions related to the canal’s width and depth, developing formulas that automatically provided the desired outcomes. For the next three decades, NRS was involved in other fields of research. In 1951, he was appointed as the Rippon Professor at the Indian Association for the Cultivation of Sciences (IACS). He delivered three lectures, which were published in the form of a booklet [8] under the title “The modern theory of turbulence”. In his first lecture, NRS reviewed the history of turbulence, beginning with Osborne Reynolds’ characterization of turbulent motion as a combination of mean and fluctuating movements. He explained that fluid flow in hydrodynamics is governed by the Navier–Stokes equations and that the Reynolds number R distinguishes flow types, with low R indicating laminar flow.
The subsequent lecture focused entirely on the statistical theory of turbulence, initially proposed by Geoffrey Ingram Taylor and further developed by researchers including Heisenberg, S. Chandrasekhar, Theodore von Kármán, and Leslie Howarth, among others. NRS discussed various methods for calculating mean values of entities such as velocity, pressure, and density in turbulent flow, focusing on their impact on fluctuating components. He began with isotropic and homogeneous turbulence and noted that although turbulence in a wind tunnel behind a grid is not perfectly homogeneous, it is statistically homogeneous to a significant extent. In his lecture, NRS discussed various theories given by Carl F. von Weizsaecker, Heisenberg, Chandrasekhar, George Keith Batchelor and Chia-Chiao Lin. NRS observed that G.I. Taylor had shown that the characteristics of isotropic turbulence could be studied using a spectrum function, which describes the distribution of turbulent energy across various wave numbers. While earlier attempts to derive this function from mechanical equations had failed, Heisenberg proposed a form that satisfied a general decay equation. NRS extended this work by providing a more general homologous solution.
In 1957, NRS noted that he had previously shown that inertia terms dominate the early stages of turbulence decay. He then analyzed self-preserving solutions to Heisenberg’s equation for isotropic turbulence and found that the spectrum following the fourth power law for small wavenumbers is stable. He concluded that the solutions by Heisenberg and Chandrasekhar are the most stable within this family, to which all previously unstable motions are likely to converge.
The above field of research was extensively worked out in Kolkata by some of his students, K.M. Ghosh, R.N. Bhattacharya and his associate M. Ray.
Ballistics, quantum-, wave mechanics and more
Fire and flame have significantly shaped the course of civilization. The study of flames is closely connected to explosions in both mines and weaponry. In 1815, English chemist Humphry Davy invented a safety lamp for coal miners, which prevented the ignition of explosive gases, ultimately saving millions of lives.
Understanding flames is crucial for rocket technology. In the 1920s, Walter Mason and Richard Wheeler from the UK discovered that when a gaseous explosive mixture was ignited at the open end of a horizontal glass tube, the flame travelled at a steady speed over a specific distance. Wheeler and his colleagues subsequently formulated a speed law to describe this phenomenon.
In Kolkata, NRS and H.K. Sen investigated ignition temperatures and discovered a correlation between ignition and flame temperatures in flammable mixtures during uniform flame propagation. They suggested that uniform flame propagation is possible when pressure effects are minimal in the initial phase. Their refined velocity equation, which accounted for temperature distribution within the gaseous medium, was confirmed through experiments with coal gas, methane, ethylene, and carbon monoxide.
The Second Defence Science Conference was held from 22–25 April 1952, chaired by A.C. Banerji, Vice-Chancellor of the University of Allahabad. The conference began with Banerji’s remarks, followed by contributions from NRS and Ram Behari. NRS emphasized the relationship between theoretical ballistics mechanics and discussed the difficulties of including ballistics in university curricula.
While his direct contributions to ballistics were limited to a single publication, he supervised several DSc theses on the subject at the University of Calcutta, including G. Deb Ray’s work on “An exact analytic solution of equations for an explosion with spherical symmetry”. The most extensive work was done by Asim Ray, who wrote several articles and a thesis titled “On some ballistic problem”.
By early 1929, Schrödinger’s wave mechanics had not yet tackled spectral line splitting in crossed electric and magnetic fields. Paul Dirac had already developed equations to explain the effects of magnetic fields on spectral lines and clarified the Zeeman and Stark effects in hydrogen. NRS investigated spectral line splitting in asymmetric crossed fields, assuming strong fields where relativistic effects were negligible. His calculations indicated that for parallel fields, the results were consistent with old quantum mechanics, while for crossed fields, he detailed the transition patterns for split H\alpha-lines.
In a separate article, NRS demonstrated that Dirac’s particle equations could be derived by averaging the \psi-functions, leading to the momentum, energy equations, and Lorentz force expression. He applied the impulse principle to a finite closed system, identified an appropriate wave mechanical Lagrangian function, and derived the equations of motion and energy. Additionally, he provided clarification on the correct interpretations of the Dirac operators.
The Kepler problem, which deals with two bodies interacting via a central force, is crucial for celestial mechanics and the study of charged particles. NRS explored how gravitational fields impact atomic structure within this context and discovered that a slight modification to the Balmer formula could account for line redshift. His analysis indicated that although the continuous spectrum persisted, the Balmer formula for discrete negative energy values was generally ineffective due to the absence of discrete solutions meeting natural boundary conditions.
Epilogue
NRS’s formative years are of great interest. His teachers, D.N. Mallik and J.C. Bose themselves were researchers whose teaching and research influenced young scholars. Before publishing his results, NRS got the chance to present them in the meetings of the Calcutta Mathematical Society, whose audience consisted of experienced researchers like Asutosh Mookerjee, C.V. Raman, Ganesh Prasad, and D.N. Mallik.
NRS’s initial scientific work was closely related to the subjects he was teaching. His studentship interaction with Arnold Sommerfeld and Max von Laue helped him consolidate his approach to the subject. In his academic career, he seamlessly combined research with teaching, thus producing a number of students who went on to carry out frontline research, so much so that the group earned the name “Kolkata School of Relativity”.
NRS took active interest in the functioning of the Calcutta Mathematical Society, and served a term as its treasurer.
On the aspect of education, NRS argued for the strengths of teaching in the mother tongue, and pushed the University Commission for science education in the Bengali language. In 1949, his book titled “Soura Jagat” (The Solar System) in Bengali was brought out by the Visva-Bharati University.
NRS was married to Binarani Sen, grand-daughter of the famous Bengali poet Nabinchandra Sen in 1927. The couple had two sons, Nitish and Pritish, and a daughter Archana. Nikhil Ranjan Sen passed away on 13 January, 1963.
Acknowledgements: First and foremost, I would like to express my gratitude to Prof. Dr. C.S. Aravinda, chief editor of Bhāvanā, for inviting me to write this article and for his editorial work. I am also grateful to Mr. Rüdiger Buchholtz, Mr. Kevin Ägerter, and Mr. Henrik Hofer from the University Archives at Humboldt University, Berlin, for providing me with documents related to NRS’s PhD thesis. Last but not least, I extend my sincere thanks to Prof. Dr. Michael Komorek of the Research Group for Physics Didactics and Public Understanding of Science for granting me access to research facilities.
References
- [1] Singh, R., Roy, S.C., N.R. Sen – Life and Science, Shaker Publisher, Düren 2021.
- [2] Sen, N.R., On the potentials of uniform and heterogeneous elliptic cylinders at an external point, Bull. Calcutta Math. Soc. 10, 1918, pp. 11–27.
- [3] Sen, N.R., On the potentials of uniform and heterogeneous elliptic cylinders at an external point, Phil. Mag. 38, 1919, pp. 465–479.
- [4] Sen, N.R., On the potentials of heterogeneous incomplete ellipsoids and elliptic discs, Bull. Calcutta Math. Soc. 10, 1918, 157–178.
- [5] Sen, N.(R). Über die Grenzbedingungen des Schwerefeldes an Unstetigkeitsflächen, Annalen der Physik, 4 (1924a): 365–396.
- [6] Sen, N.R., On Eddington’s problem of the expansion of the universe by condensation, Proc. R. Soc. Lond. 140, 1933, pp. 269–276.
- [7] Sen, N.R., On the stability of cosmological models with non vanishing pressure, Zeitschrift Astrophys. 10, 1935, pp. 291–296.
- [8] Sen, N.R., The modern theory of turbulence, Indian Association for the Cultivation of Science, Calcutta 1956.
- [9] von Laue, M. and Sen, N.R., Die de Sittersche Welt, Annalen der Physik, 379 (1924a): 252–254.
- [10] von Laue, M and Sen, N.R. Über die berechnung des potentialabfalles in den von glühenden metallen ausgesandten ionen und elektronengasen, Annalen der Physik, 380 (1924b): 182–188.
Vishnu Vasudev Narlikar (1908–1991)
By Aragam R. Prasanna
Retrospective prelude
It was in February 1966, that P.C. Vaidya was visiting the institute of Mathematical Sciences (Matscience) in Chennai and gave a course of ten lectures on “Selected Topics on Gravitation’’, of which I prepared the lecture notes as I was a student there. I had joined Matscience in October 1965 and had decided to work in the field of general relativity. After going through my work till then, Vaidya suggested that I could work for my PhD with V.V. Narlikar (VVN) who was coming to the University of Poona as Lokamanya Tilak Professor.
Accordingly I wrote to VVN and after an interview he accepted me as a student and offered me a University scholarship. I joined the mathematics department of Poona University in October 1966 and started working with him. The first lesson I learnt, apart from relativity, was to be punctual. Every day in the afternoon the students were supposed to meet him in his chambers exactly at 2 PM (not a minute earlier or later) and report whatever work one had carried out during the previous 24 hours.
I worked mainly on the geometrical aspects related to different spacetime metrics and the curvature underlying the manifold. VVN used to go through my submissions and would question me when I had to explain on the board my responses. Sometimes he used to suggest alternative aspects to be looked into. Our working days were from Monday to Saturday, with no breaks. The rigours of working like that has stood me in good stead, which I have respected and enjoyed all through my life.
Having worked continuously for almost two years, I went to him, before Diwali of 1968, asking permission to go home (Bangalore) for a month. The response still lingers in my mind. “Mr. Prasanna, leave is not a right, it is only a privilege, you may go for two weeks.” At the same time, VVN and Mrs. VVN were both very affectionate, and used to invite students on festival occasions to share sweets with them. The time I spent in Poona (Oct 66 to Dec 69) was extremely beneficial to me and if I could do some good research later in my life the foundation was laid in Poona by Professor V.V. Narlikar.
Professor V.V. Narlikar: A biographical sketch6
Professor Vishnu Vasudev Narlikar was born at Kolhapur, Maharashtra, on 26 September 1908, in a scholarly family. His father Sri Vasudev Shastri was a well-known Vedic scholar. As a child, Vishnu was of rather poor health; however, because of the extra care from his parents, he survived through difficult days. He had his schooling at Rajaram High School and after securing distinction in his matriculation, which earned him the Le Grand Jacob Scholarship, he went to Bombay in 1924 to pursue his studies at Elphinstone College and the Royal Institute of Science.
Apparently to continue his family traditions Vishnu wanted to take up Sanskrit literature but did not do so as he did not secure the first place in that subject. He then decided to do mathematics, which in fact was a good turn of fate as he was later to establish a school in mathematics particularly in General Relativity in the country. His love of Sanskrit did indeed never diminish and on his own he studied the language and its literature all his life.
At Bombay he had a very distinguished career and at the BSc (Hons.) examination in 1928 he scored first class first and set a new record in mathematics. With this background it was not difficult for him to go to England to pursue his studies in mathematics, obtaining the necessary financial assistance from J.N. Tata Endowment, from Kolhapur State and also the Sir Mangaldas Nathubhai Travel Fellowship from Bombay University.

VVN returned to India in 1932, though he had a fellowship at Cambridge to continue for another two years. It was Pandit Madan Mohan Malaviya who was instrumental in Narlikar’s return. Malaviya Ji, the then Vice Chancellor of Banaras Hindu University (BHU), while on a visit to England, learnt about VVN and offered him the chair of Mathematics at BHU. VVN was then only 24 years of age, and what a prestigious offer!

In 1938, VVN delivered a series of lectures on Gravitation at Bombay University and during these lectures he pointed out that the then only known exact solution of Einstein’s equations was the Schwarzschild solution for a static mass M. However, it is known that stars radiate and thus have an envelope of atmosphere filled with radiation and thus to depict the field of a star one will have to consider the region just outside the stellar surface not empty as in Schwarzschild case but filled with radiation having non-zero density. This, according to him, was one of the outstanding problems that needed consideration. Accordingly, when young P.C. Vaidya (PCV) went to BHU to work with VVN, in 1942, he suggested that they work on the problem of the field of a radiating star and after a brilliant suggestion from Vaidya regarding the nature of energy-momentum tensor to be considered, VVN derived the first tangible equation. However, before their next sitting, PCV had not only completed the formulation but also had solved the equations completely. To complete this story in the words of PCV, “We wrote down the final solution in the form of a paper for publication. Narlikar put down only my name as the author of the paper, though the usual practice was that the Professor who suggests the problem becomes the first author. But VVN did not follow this routine because the main idea which provided the breakthrough was given by me and so he gave full credit to me. Today, when I think about it, I realize that VVN very well knew the importance of the solution and even if he had just added his name as a joint author, the solution would have been known as `Narlikar metric’ instead of `Vaidya metric’. But VVN preferred to stick to purer academic norms and decided that the credit should go to the one who gave the principal idea.” What a fine example of academic integrity!
Geheniau, who went through the paper came back the next day and acknowledged that they must be called the “Narlikar–Karmarkar invariants”
In fact this solution has been hailed as one of the most important solutions in General Relativity and work on different aspects of it was pursued internationally and even now there are newer aspects of it under consideration. In the following years VVN published several articles in collaboration with PCV on the interpretation of the radiation field associated with the Vaidya metric.

Regarding the paper on Scalar Invariants of a four-dimensional curved manifold, the story as I have recounted elsewhere is as follows: In 1922 T.Y. Thomas, a noted mathematician, had proved that in a four-dimensional Riemannian manifold only fourteen independent curvature invariants of second order can be constructed, as the metric tensor g_{ij} and the Riemann–Christoffel curvature tensor R_{hijk} together have thirty independent components connected by sixteen independent differential equations. But the explicit construction of these fourteen invariants using g_{ij}, R_{hijk} and the Weyl tensor C_{hijk}, was given only in 1949 by VVN and his student Karmarkar. However, as this paper was published in the Proceedings of Indian Academy of Sciences, it was not known in the outside world. Ehlers and Kundt, writing on differential invariants in their article “Exact Solutions of the Gravitational Field Equations”, in the book Gravitation (edited by L. Witten), attribute the explicit construction of the fourteen invariants to Geheniau and Debever, who did it in 1956, i.e., seven years after the paper of Narlikar and Karmarkar. I had seen this article as a student in 1968 and the first time I met Geheniau and Ehlers in 1972 at the Dirac Symposium at Trieste, I showed the paper of Narlikar and Karmarkar to them, pointing out the misplaced attribute. Geheniau, who went through the paper came back the next day and acknowledged that the attribute should really go to these authors and even said that they must be called the “Narlikar–Karmarkar invariants”. However, as not much work has been done since then with these invariants, it has not yet been possible to realize in print the name Narlikar-Karmarkar invariants. One hopes that this will get rectified appropriately by mathematicians who might have the occasion to use these invariants and the due credit will be given to VVN and Karmarkar.

VVN was a great teacher apart from being a leading research worker of his time. As PCV puts it, he was a teacher-mathematician, who used teaching methods in his research and research methods in his teaching. When he was asked as to what had been the source of inspiration for being a good teacher, his reply was, “My main source of inspiration has been all along a quotation from the book The Imitation of Christ—I teach without noise of words, without confusion of opinions, without ambition of honour and without the strife of arguments.” This quotation has often helped me in my dealings, particularly with students as a philosophy of life wherein one would do what is expected of them without worrying too much about the awards. Another important aspect I always bore in mind was the dictum – one cannot teach without learning – and thus I always tried to keep pace with new developments. In fact, this was also the advice given to me by Professor Larmor at Cambridge who often said, “A teacher must always be in a position to learn new things. In my opinion this is the basic understanding one needs to have for being a researcher as well as a teacher.” This essentially notes how “introspection” is a must for any teacher. In another interview he had said, “When I started teaching mathematics at Banaras, I was more self-critical and I found that there were many gaps and voids in my understanding of the topic I taught. The first lesson that I learnt was: one cannot be a good teacher, a successful teacher without always being absorbed in research topics concerned with his lectures.”
His scholarship went beyond mathematics. He had invitations from various societies to lecture on various topics. Mrs. Narlikar recounts how the friendship bond between VVN and S. Radhakrishnan got stronger after once Radhkrishnan heard VVN give a lecture on aspects of Sikhism to the Sikh Students’ Union at BHU. Being asked how he was so familiar with Sikhism, VVN seems to have replied that he is interested in and affectionate towards all religions and before giving a lecture on any topic he prepared with great care. Interested as he was in all religions, he was against rituals, casteism and untouchability. He helped Harijan students and guided them.
one cannot be a good teacher, without always being absorbed in research
VVN stayed at BHU till 1960 and then moved to Ajmer where he served as Chairman of Rajasthan Public Service Commission for six years. In 1966 he moved over to Pune, where he returned to academic life as Lokmanya Tilak Professor of Applied Mathematics at the University of Poona. It was here that I had the privilege of working with him from October 1966 to November 1969 for my PhD degree. Apart from Relativity the most important lesson I learnt was self-discipline and punctuality. During his tenure as Tilak Professor (1966–1973), about half a dozen students got their PhD degrees under his guidance working on various physical and geometrical aspects of Riemannian metrics representing solutions of Einstein’s equations for various energy-momentum distributions.

Professor V.V. Narlikar was a Founder Fellow of all the three Science Academies, the Indian Academy of Sciences in Bangalore, the Indian National Science Academy in Delhi and the National Academy of Sciences in Allahabad. He was also a Fellow of the Royal Astronomical Society, London and was President of the Calcutta Mathematical Society (1958–60) and of the Indian Mathematical Society (1981).
During an interview when I asked him as to what has been the main philosophy of his life and message to younger generations, he replied, “Every person has to learn to distinguish between his needs and wants. I have always felt that nature comes to your rescue where your needs are concerned and your parents, relatives and friends fulfil your wants. Needs are for your soul, the upliftment of which comes from trying to understand nature, while one’s physical well being is looked after by people around.’’
The early days of general relativity7
By Jayant V. Narlikar
This account deals with the progress of Einstein’s general relativity (GR) theory first published in 1915. It will discuss the “bending of light” experiment planned and executed by Eddington in 1919 and then concentrate on the development of GR in India. For, it will be argued that despite the reputation of GR as an obtuse theory it did find fertile soil to grow in India. This account will go as far as the time of India’s independence.
Introduction
I begin with a stanza in a verse written by a member of the American Mathematical Society. The different stanzas pay tributes to various famous mathematicians. The last one is about Einstein:
To Einstein, hair and violin,
We give our final nod;
Though understood by just two men,
By himself and sometime by God.
This stanza recalls the early phase soon after GR was published as a theory. To physicists it appeared very weird in the sense that it did away with gravity as a force but slipped it back in as a manifestation on non-Euclidean spacetime geometry. To mathematicians, accustomed to thinking of non-Euclidean geometries as notebook exercises with no contact with reality, the GR claimed to produce measurable effects.
Thus the acceptance of the newly created GR required a cautious approach. Ten years earlier, Einstein’s special relativity (SR) theory had evoked considerable reaction from physicists as well as laymen. That may have been because the concepts introduced by SR, though revolutionary, could be related to real life experiences and doable experiments. The GR in comparison suffered from difficult concepts like curved spacetime and lack of many experiments to test the theory.
The bending of light
It was against this background that Eddington thought of the bending of light experiment to test the Einstein hypothesis against the Newtonian prediction. The basic idea is simple.
For a Sun-like massive body of mass M, the ray of light coming from a star S, would be slightly bent by the star’s gravity so that it enters the viewer’s telescope at a slightly different angle than when no such massive body played a role of “light bender”. The star image would shift by a calculated angle
\[
\delta\alpha_{E}=\left[\frac{GM}{c^2R}\right] \cong 1.75\left(\frac{M}{M_{\odot}}\right) arcsec.
\]
What does Newtonian theory say? When quizzed on whether massive objects can bend light rays, Newton refused to answer because he had always been reluctant to speculate. Non fingo hypothesis (I do not speculate) is what he would say in reply. He listed the question amongst his collection of unsolved queries.
But others following him with specific assumptions got a definitive answer. For example, if we take a light quantum of frequency \nu, its energy is h\nu and by SR-type argument its mass is h\nu/c^2. Such a quantum subject to Newton’s laws of motion will give a bending by the angle
\[
\delta\alpha_N \cong 0.87\left(\frac{M}{M_{\odot}}\right) arcsec.
\]
That is, the Newtonian value is half the Einstein one. Thus we had here theoretical predictions from GR and (amended!) Newtonian theory with the former twice the latter. Which one, if any, will survive a test to measure bending of light?
This provided a potential test provided one could photograph stellar images close to the solar disc. There is only one situation when one can photograph stars in the sky with the Sun around: the occasion of total solar eclipse. Eddington, the mathematician and astronomer was one of the very few people who really understood GR and felt the need for carrying out such a test. The 1919 total solar eclipse provided the necessary background for this experiment.
For details of this experiment and its aftermath see references 1–3. At a joint meeting of the Royal Society and the Royal Astronomical Society on 6 November 1919, Eddington announced the findings of his team and argued that the data favoured Einstein’s rather than Newton’s value (see [1]).
This experiment has been repeated several times at different eclipses. Although progressively the observational techniques improved, all optical measurements carry a number of error-bars. As radio and microwave technologies became available the experiment could be performed with very small error-bars. Two such experiments are described in [2] and [3], using radio and microwaves respectively.
The 1919 experiment though, being a pioneering one, had a tremendous influence on the reception accorded to GR and to Einstein. The experiment showed GR to be a testable scientific theory despite its abstruse formulation. It raised Einstein from the general level of a distinguished scientist to an all-time genius of the rank of Newton.
The 1919 experiment raised Einstein to an all-time genius of the rank of Newton
Looking back, though, one finds several “holes” in the way the 1919 experiment was conducted and how the data were reduced. For a graphic account of the experiment as reviewed from modern times, see the article by Peter Coles [4].
For the Indian angle it is worthwhile to recall that the Kolkata paper Statesman published a detailed account of what the experiment was about. This was written by a young physicist, Meghnad Saha who later became famous for his astrophysical contributions.
It is a measure of the importance the media attached to this experiment that the Statesman had a special article on it followed by reader’s correspondence. The article by Saha is a good one and shows that writing on science at a popular level was not unheard of, if not very common.
Two schools
In the year 1911, three bright young scientists started their careers in mathematics and physics, more specifically, applied mathematics and theoretical physics. These were the first three on the merit list of the intermediate examination in Bengal (equivalent to Std XII today). The topper was Satyen Nath Bose, who went afterwards for particle physics, second was Meghnad Saha (who wrote the article on bending of light) and the third was Nikhil Ranjan Sen (NRS). Saha went for astrophysics and NRS opted for applied mathematics.
Bose was destined to play a key role in the developing field of quantum mechanics. His work on quantum statistics resulted in a whole family of particles being named “bosons”. Saha’s work on the ionization equation started a major new area of work on stellar atmospheres. Indeed Eddington’s classic work on stellar structure could be undertaken because of Saha’s equation providing the vital details of the surface conditions for stars.
It was the third boy who opted for applied mathematics; NRS went to Germany for PhD and higher research, worked with von Laue on GR and cosmogony at Berlin University and returned to India with great enthusiasm for the newly emergent GR. Interested in a wide range of subjects within applied mathematics, NRS had special interest in GR. As research in GR started to grow around him, Kolkata in the late twenties acquired a reputation of hosting the first school on general relativity in India.
A few years later, in 1932 a second school on GR began to develop around Vishnu Vasudev Narlikar (VVN) at the Banaras Hindu University (BHU).
VVN had been studying in Cambridge. After a brilliant career at the Mathematical Tripos, he continued at Cambridge as an Issac Newton student. This was a research scholarship usually given to the topmost astronomy student passing the final part of the Tripos. By virtue of his research interests VVN had good interaction with famous figures at Cambridge – in particular Eddington, astronomer W.M. Smart and mathematical physicist Joseph Larmor. While a research student VVN distinguished himself by winning the Rayleigh Prize.
His laurels spread and they attracted the attention of Pandit Madan Mohan Malaviya, who had founded the Banaras Hindu University in 1916. Ever on the lookout for highly talented staff and students for this budding seat of learning he took advantage of the Round Table Conference in London to come over and meet VVN. At the meeting Malaviya made a promise of giving him a senior post so that he could develop mathematics at the BHU.
In 1932 VVN was due to go to USA for a year’s work at the Mt Wilson Observatory of Caltech. Prior to that he had planned to spend 2/3 months in India. While on this long vacation he decided to visit BHU and see how the organization was functioning. Malaviya welcomed him and showed him around. Thereafter he made an offer that VVN could not refuse. He straight away joined as Professor and Head of the Department of Mathematics. This was shortly to grow into the second thriving school of GR in India.
NRS and the Kolkata School
Being a theoretician with strength in applied mathematics, NRS looked for solutions of Einstein’s equations with mathematically significant properties. We briefly describe a few of such solutions.
Static and spherically symmetric solution: NRS obtained a solution which showed a static but spherically symmetric system in its most general form, as seen in [5]. This is based on Einstein’s solution of a cluster of particles each moving in a circular orbit, with these particles distributed so that each moves in the field of others.
The list prepared by Andrzej Krasinski of important papers in GR (“Golden Oldies”) includes NRS’s article on stability of cosmological models (see [6]).
Another rather curious result by NRS describes a spherical shell of matter in an otherwise empty space. A coordinate transformation of the solution inside the shell leads to the de Sitter spacetime!
As an excursion into the area wherein electro-magnetic energy tensor produced by charged particles acts as a source of gravity, NRS obtained the equilibrium condition for a charged particle with definite spherical boundary [7].
NRS found that for any charge distribution in the spherical volume, three-fourths of the total energy of the particle are electrical and one-fourth gravitational, provided the charge distribution is describable by an analytical function.
In the early 1930s, carried over by the general excitement of the “expanding universe”, NRS looked at models not perfectly spherically symmetric. He showed that it is possible to have static universe models in equilibrium provided the total mass of such a universe exceeds the mass of the static Einstein universe. This conclusion could be linked with the question, why the universe is expanding.
While NRS guided a number of students in GR to their PhD degree, there appears to be one loner whose work we describe next.
Who was B. Datt?
While reading the Landau–Lifshitz text book Classical Theory of Fields (2nd edn.), I came across a reference to the paper by one “B. Datt”. As a postdoc working on gravitational collapse, I found Datt’s approach quite general. In fact, as I discovered, the Landau–Lifshitz text followed the method used by Datt. This work of Datt [8] was published in 1938.
As I discovered, the Landau–Lifshitz text followed the method used by Datt
A year later Oppenheimer and Snyder wrote a paper [9] with similar material content so far as the technique of handling the GR equations goes. The Oppenheimer–Snyder paper is generally regarded as the pioneering work on spherical massive objects contracting with increasing inward speed. Datt, however, kept his approach general; thus giving solutions not only of contraction but other motions too. More importantly, he had seen the significance of co-moving coordinates in solving such problems.
At this stage one may very well ask, what later work by Datt is found in GR literature. The answer, prima facie, is nil. Indeed, my enquiries with relativists from Kolkata belonging to Datt’s generation drew a blank. It was more recently reported by Somak Raychaudhury that Datt belonged to the famous Presidency College (now elevated to the university status) and was a favourite student of NRS. As to why no later work by him is reported, the answer is tragic: around 1940 he died in the course of a surgery that went wrong.
One cannot help but recall two distinguished GR workers who died at a young age after producing important work: Karl Schwarzschild and Alexander Friedmann. The former took part in World War I and while serving on the German front in Russia, contracted a rare but painful skin disease called pemphigus which may have led to his demise in 1916. Friedmann died of typhoid which he caught during a holiday in Crimea.
Unified field theory
Einstein regarded GR as a stepping stone towards a more comprehensive theory that, ideally, would include all basic physical interaction under one umbrella. As a starting point he attempted bringing the electromagnetic theory and gravitation together as a “Unified Field Theory”.
Several scholarly scientists were tempted to join the search for a unified theory. One finds such names as S.N. Bose, Gangopadhyaya, Mahadeo Dutta, etc. from the Kolkata region with occasional contributions by VVN from the Banaras school. In particular, VVN’s review talk [10] as President of the mathematical section of the Indian Science Congress 1947 gives an updated version of the unified theories then under discussion.
However, as is well known, attempts abroad or in India to find a unified field theory did not succeed. Although disappointing in a way, the ideas like Kaluza-Klein theory (see [11] and [12]) which were the outcome of use of higher dimensions for a unified field theory have found use in modern theoretical cosmology.
VVN and the Banaras School
We now come to the Banaras School started by VVN.
In a private communication, VVN has described an incident in Cambridge involving Eddington and himself. Early in the 1930s, VVN solved Einstein’s equations with as well as without the \lambda-term to generate models of the expanding universe. At the time Hubble’s observations had indicated an expanding universe. VVN had simplified the problem by assuming the space to be homogeneous and isotropic. When he showed his calculations to Eddington (who was one of his research advisers). Eddington was very impressed with the work and offered to communicate it to an astronomy journal.
However, while the paper was getting ready for submission, Eddington received a letter and a paper by Abbe’ Lemaitre. The letter requested Eddington to arrange publication of an English translation of the attached paper in French which was published in 1927 (see [13]).
When Eddington read the French paper he realized that Lemaitre had already (in 1927) done the same work which VVN had recently reported to him. So he called VVN to explain that the work in question had already been done and published in 1927. Being in French and in a journal not very well known he had missed it. He therefore could not communicate VVN’s paper although he regretted the extra work VVN was put to in writing it. As a post-script, I may add that even Lemaitre’s paper had been “anticipated” by a couple of papers by Alexander Friedmann (see [14] and [15]).
When VVN settled down in the campus of BHU he carried on his research in GR. Some of the work done by the Banaras School (VVN and his student) is highlighted next.
The GR being a nonlinear theory with a complicated set of partial differential equations, there are very few exact solutions known. This area of exact solutions therefore interests the mathematicians who like their models to be precise and not approximate.
Some BHU workers did research on the unified field theory of Einstein and Schrödinger (see [16]). In terms of worldwide perception unified field theories became increasingly isolated as most physicists believed that unification should proceed in another order:
em theory \rightarrow em + weak theory (electroweak theory) \rightarrow electroweak + strong theory (grand unified theory) \rightarrow grand unification + gravity \rightarrow complete unification.
Thus gravity comes in the end rather than in the beginning and also the present approach requires gravity to be quantized – a stage not yet reached even today.
Highlights of work from BHU
Some of the relevant work from the Banaras school may be described as below:
In 1922 the noted mathematician, T.Y. Thomas had proved that in Riemannian manifolds of four dimensions only 14 independent curvature invariants can be constructed. But the explicit construction of these 14 invariants using the curvature tensor and the Weyl tensor was first given by Narlikar and Karmarkar [17]. However, this work was published in the Proceedings of the Indian Academy of Sciences, a journal which did not have much circulation outside India. Unaware of this work therefore, several years later Geheniau and Debever in 1956 did the same work for which they were given credit (see [18]). This was noticed by A.R. Prasanna, a student of Narlikar at Pune who pointed out to Geheniau this fact when they met in 1972, at the Dirac Symposium at Trieste. Geheniau readily agreed that these invariants should be called “Narlikar–Karmarkar invariants”.
These invariants are important in deciding if a space-time manifold has singularities. The question of singularities became relevant to reality by the discovery of collapsed massive objects in the form of quasars in 1963. Will the spacetime in the neighbourhood of such massive objects develop a singularity? If so, how to spot it in a coordinate–invariant fashion? This is where the curvature invariants become important.
![1973 letter from VVN that carries a mention of the 14 [Narlikar–Karmarkar] invariants.](https://bhavana.org.in/wp-content/uploads/2024/10/JVN_letter01-1024x704.jpg)
Work of a more mathematical nature came out of the studies of Narlikar and his students Ramji Tiwari and Kamala Prasad Singh. Tiwari was concerned with the unified field theory proposed by Einstein in the late 1940s and examined in detail the interaction between gravitation and electromagnetism (see [19]). Singh on the other hand worked on metric invariants. His work on the Christoffel symbols is of interest in bringing out the role of coordinate transformations that lead to indeterminateness (see [20]).
General relativity has the unique feature that it contains the equations of motion of the gravitational sources and the method of deriving them was indicated by Einstein, Infeld and Hoffmann (see [21]). Narlikar’s student, B.R. Rao worked on the details of this problem and pointed out some corrections to the EIH work. This was recognized by Infeld and Hoffmann. The Narlikar–Rao paper [22] appeared in print in the year following Einstein’s death.
The Vaidya solution
P.C. Vaidya (PCV) started his research career as a student of VVN. Himself a postgraduate of Bombay University, Vaidya enrolled himself as an external research student of Narlikar in BHU in 1942–43. Essentially living on his savings he made them stretch out to last for this period (during which he also had to support a family of wife and child). Yet during those two years PCV was able to produce work that was to prove to be of very special interest to relativistic astrophysics about 25 years later.

The 1950 paper [23] quotes VVN: “If the principle of energy is to hold good, that is, combined energy of the matter and the field is to be conserved, the system must be an isolated system surrounded by flat space-time. A spherical radiating mass would probably be surrounded by a finite and non-static envelope of radiation with radial symmetry. This would be surrounded by a radial field of gravitational energy becoming weaker and weaker as it runs away from the central body until at last the field is flat at infinity. It has to be seen whether and how this view of the distribution of energy is substantiated by the field equations of relativity.” This conjecture was borne out by the Vaidya solution.
To start with, take the four spacetime coordinates as x^0=t, x^1=r, x^2=\theta, x^3=\phi. A star of mass M and radius r_0 is supposed to start radiating at time t_0 and as time goes on, the zone of radiation increases in thickness, its outer surface at time t=t_1 > t_0 being given by r=r_1 > r_0. For r_0 \leq r \leq r_1 and t_0 \leq t \leq t_1, the line element is given by
\[
ds^2 = e^{\nu}dt^2 – e^{\lambda}dr^2 – r^2 (d\theta^2 + sin^2\theta\,d\theta^2).
\]where both \lambda and \nu are functions of r, t only. The outflowing radiation is described by the energy momentum tensor
\[
T^{ik}=\rho\nu^i\nu^k,
\]where \rho is the density of radiation and \nu^i is the null vector representing its flow direction. For radial flow, of course, we have \nu^2=\nu^3=0.
The field equations then give (with G=1, c=1)
\[
e^{-\lambda}= 1-\frac{2m}{r}, m=m(r,t),
\]and
\[
e^{\nu/2}=-\frac{ṁ}{m’}\left(1-\frac{2m}{r}
\right)^{-1/2},
\]
where m satisfies the relation
\[
m’\left(1-\frac{2m}{r}
\right)=f(m).
\]The dot and dash denote differentiations with respect to t and r respectively.
The function f(m) is so far arbitrary but needs to be specified by the physical conditions that lead to the radiation from the star, whose mass m decreases at a rate determined by the amount of energy radiated by it. The radiation envelope of the star is described by the line element
\[\begin{align*}
ds^2=\frac{ṁ^2}{f^2}\left(1-\frac{2m}{r}
\right)dt^2 – \left(1-\frac{2m}{r}
\right)^{-1}dr^2 – r^2(d\theta^2)+\sin^2\theta\,d\phi^2.
\end{align*}\]
The energy conservation relation is described by the condition
\[
\frac{dm}{d\tau} \equiv \nu^0\frac{dm}{d\tau}+\nu^1\frac{dm}{dr}=0.
\]Of course, this equation is automatically satisfied if all field equations are satisfied.
This formalism has been useful in the context of bright radiating objects in astrophysics, such as quasars, active galactic nuclei, gamma ray bursts, etc.
PCV has recorded that the problem as such was posed by VVN as a research area for PCV. Having stated the problem VVN proceeded to solve it. There were three equations of which VVN solved the first one, leaving the remaining two to be solved by PCV.
At this stage there was a gap of a few days when VVN was out of BHU on some official work. It was his practice both in teaching and research to pause halfway in his work and leave a time gap for the student to think for himself and proceed on his own if possible. In this particular case when VVN came back PCV was ready with the solution.
PCV also mentions that he had put the names VVN and PCV as joint authors of this work. However, VVN overruled him and stated PCV as the sole author.
Concluding remarks
VVN had occasional correspondence with the astrophysicist S. Chandrasekhar (Chandra) with whom he had overlapped for two years at Cambridge. After Vaidya’s work, VVN asked Chandra if there were any areas in astrophysics where GR could be profitably applied. Chandra replied in the negative with his conjecture that gravity would not be strong enough in astrophysical situations to demand GR!
This concludes our account of GR in its early stages starting from its creation to the contributions made by Indian scientists in British-ruled India. This period may be considered (worldwide) as an era of understanding what GR really means. Subsequent to Einstein’s death in 1955, events happened which led to a diversification of the menu of problems tackled including gravitational radiation, topological and structural problems of space-time, Mach’s principle, cosmological models, etc. And quasars brought in GR specialists to work on relativistic astrophysics, contrary to Chandra’s expectations. This era will be covered in another paper.\blacksquare
References
- [1] Dyson, F.W., Eddington, A.S. and Davidson, C., A determination of the deflection of light by the Sun’s gravitational field, from observations made at the total solar eclipse of 29 May 1919. Philos. Trans. R. Soc., 1920, A220, 291.
- [2] Counselman III, C.C., Kant, S.M., Knight, C.A., Shapiro, I.I. and Clark, T.A., Solar gravitational deflection of radio waves measured by very long baseline interferometry. Phys. Rev. Lett., 1974, 33, 1621.
- [3] Fomalont, E.B. and Sramek, R.A., A confirmation of Einstein’s general theory of relativity by measuring the bending of microwave radiation in the gravitational field of the Sun. Astrophys. J., 1975, 199, 749.
- [4] Coles, P., Einstein, Eddington and the 1919 eclipse. In The Historical Development of Modern Cosmology (eds. Martinez, V.J., Trimble, V. and Pons-Borderia, M.J.), ASP Conference Series, 2001, vol. 252.
- [5] Sen, N.R. and Roy, T.C., On a steady gravitational field of a starcluster free from singularities. Z. für Astrophys., 1954, 34, 84.
- [6] Sen, N.R., On the stability of cosmological models. Z. Astrophys., 1934, 9, 215.
- [7] Sen, N.R., On the electric particle according to Einstein’s field theory. Z. Phys., 1927, 40, 667.
- [8] Datt, B., On a class of solutions of the gravitation equations of relativity. Z. Phys., 1938, 108, 314.
- [9] Oppenheimer, J.R. and Snyder, H., On continued gravitational contraction. Phys. Rev., 1939, 56, 455.
- [10] Narlikar, V.V., From general relativity to a unified field theory. Presidential Address to Mathematics Section at the Lucknow Indian Science Congress, 1953.
- [11] Kaluza, T., The unification problem in physics. Sitzungsber. Preuss. Akad. Wiss (Berlin), 1921, p. 966.
- [12] Klein, O., The atomicity of electricity as a quantum theory law. Nature, 1926, 118, 516.
- [13] Abbe’ Lemaitre, G., A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extragalactic nebulae. Ann. Soc. Sci. Bruxelles, 1927, XLVII A, 49.
- [14] Friedmann, A., Uber die krummung de Reumes. Z. Phys., 1922, 10, 377.
- [15] Friedmann, A., Uber die krummung de Reumes. Z. Phys., 1924, 21, 326.
- [16] Schrödinger, E., Space-Time Structure, Cambridge University Press, 1950.
- [17] Narlikar, V.V. and Karmarkar, K.R., On the algebraic invariants of the four-dimensional Riemann tensor. Proc. Indian Acad. Sci., 1949, 29, 91.
- [18] Geheniau, J. and Debever, R., Invariants of general relativity. Bull. Acad. Belg., 1956, 42, 114.
- [19] Narlikar, V. V. and Tiwari, R., Proc. Nat. Inst. Sc., 1949, 14, 73.
- [20] Narlikar, V.V. and Singh, K.P., Proc. Nat. Inst. Sc., 1951, 17, 311.
- [21] Einstein, A. Infeld, L. and Hoffmann, B., The gravitational equations and the problem of motion. Ann. Math., 1938, 39, 65.
- [22] Narlikar, V.V. and Rao, B.R., The problem of motion in general relativity. Proc. Nat. Inst. Sci., 1956, A21, 416.
- [23] Vaidya, P.C., The external field of a radiating star in general relativity. Curr. Sci., 1943, 12, 183.
- [24] Vaidya, P.C., The gravitational field of a radiating star. Proc. Ind. Acad. Sci., 1950, 33(5), 264.
- The Senior Wrangler is the top mathematics undergraduate at the University of Cambridge in England. ↩
- Smith’s Prize was the name of each of two prizes awarded annually to two research students in mathematics and theoretical physics at the University of Cambridge from 1769. Following the reorganization in 1998, they are now awarded under the names Smith-Knight Prize and Rayleigh-Knight Prize. ↩
- (The Doctor of Science (DSc) is of a higher standing than either a masters degree (such as the Master of Science (MSc)) or the degree of Doctor of Philosophy (PhD) and is awarded for work that makes an original, substantial and distinguished contribution to knowledge in a field with which the faculty is concerned.). ↩
- Minutes of Senate, provisional committee 1921, pp. 714–715 and Report of Syndicate 1921, p. 69. ↩
- Minutes 1924, pp. 343–344. ↩
- This article was originally published in Journal of the Indian Mathematical Society, vol. 61, nos. 1–2 (1995) pp. 1–6. We thank the Indian Mathematical Society for the permission to republish, with minor edits, in Bhāvanā. ↩
- This article was originally published in Current Science, vol. 109, no. 12, 25 December 2015, pp. 2214–2219. We thank the Current Science Association, Bengaluru for the permission to republish, with minor edits, in Bhāvanā.↩
