The bhāvanā in Mathematics

The Sanskrit word bhāvanā was used by ancient Indian algebraists to name a principle of “composition” introduced by Brahmagupta (born in 598 ce) way back in the seventh century.

In mathematics, a law of composition combines (i.e., “composes”) two mathematical objects of a certain type to produce a third object of the same type; for instance, it may combine two solutions of a given equation to generate a third solution of the equation, or it may combine two polynomial expressions of a particular form to yield another expression of the same form.

Brahmagupta is the first known mathematician to state (in 628) a non-trivial principle of composition. For any arbitrary N, Brahmagupta’s composition law [equation \(\eqref{brahmaguptas-law}\)] shows how to combine two solutions of the equation Nx^2~+~z~=~y^2 to produce a third solution. In particular, it combines two expressions of the form y_1^2-Nx_1^2 and y_2^2-Nx_2^2 to get a third expression y_3^2-Nx_3^2. The precise identity that one gets [equation \(\eqref{brahmaguptas-identity}\)] is now called “Brahmagupta’s identity”.

In Europe, Brahmagupta’s identity would reappear in the works of L. Euler during the eighteenth century. Euler called the identity theorema eximium (a theorem of capital importance) and theorema elegantissimum (a most elegant theorem). While this specific identity on the important binary quadratic form y^2-Nx^2 is now a basic result in number theory, the real greatness of Brahmagupta’s bhāvanā lies in its manifesting the very principle of composition in mathematics, a principle that pervades the whole of modern algebra and number theory. But, as is the case with many outstanding mathematical discoveries in ancient India, this master stroke of Brahmagupta and its significance have not always been adequately highlighted in accounts on history of mathematics.

A subsequent major landmark in number theory is Gauss’s composition law (1801) on binary quadratic forms ax^2+bxy+cy^2 having a given discriminant D~(=~b^2-4ac), a generalisation of Brahmagupta’s identity. Around the beginning of the present century, Manjul Bhargava (recipient of the Fields Medal in 2014) stunned the world of mathematics by his discovery of new “composition laws”. His Ph.D. thesis (2001) presented a simplification and far-reaching generalisations of Gauss’s law.

In this article, we shall describe the statement and a few applications of the bhāvanā, discuss some aspects of the significance of the bhāvanā in mathematics, and briefly trace the evolution of composition laws from Brahmagupta to Bhargava. A more detailed exposition is being prepared in [1].

Brahmagupta’s bhāvanā on the varga-prakṛti

The great achievements of ancient Indian mathematicians include their ingenious methods for finding integer solutions of equations. In the chapter Gaṇita of his treatise Āryabhaṭīya (499 ce), Āryabhaṭa describes a method (subsequently called kuṭṭaka) for solving, in integers, the linear indeterminate equation ay-bx=c with integer coefficients a,b,c. In the chapter Kuṭṭakādhyāyaḥ of his magnum opus Brāhma-sphuṭa-siddhānta (628), Brahmagupta takes up the much harder problem of finding positive integer solutions to the quadratic indeterminate equation Nx^2+1=y^2 for a fixed positive integer N. The equation was later called “Pell’s equation” in modern Europe. Since Brahmagupta is the first mathematician to investigate this important equation in a general framework, the equation is nowadays being renamed as the Brahmagupta–Pell equation.

It is in the context of this specific equation Nx^2+1=y^2 that Brahmagupta formulates his composition law on the space of the (undetermined) solutions of the more general equation Nx^2+z=y^2. Such equations were called varga-prakṛti (square-nature) in ancient India, a fitting name as the problem involves finding a square x^2 whose product with a given non-square N would again become a square y^2 after adding (a small integer) z, preferably 1. Brahmagupta’s bhāvanā combines two solutions (x_1,y_1,z_1) and (x_2,y_2,z_2) of the varga-prakṛti Nx^2+z=y^2 to produce a third solution (x_3,y_3,z_3), given by x_3=x_1y_2+x_2y_1, y_3=Nx_1x_2+y_1y_2 and z_3=z_1z_2. Using the notation (m,n;c) for three numbers satisfying Nm^2+c=n^2 and \odot for the composition operation, Brahmagupta’s law takes the form

The technical power of Brahmagupta’s law can be seen from the ease with which it provides a two-step integer solution to the otherwise difficult equation 92x^2+1=y^2 presented in Box 1.

Box 1. Application of bhāvanā: the case N=92

Example (Brahmagupta). Solve, in integers, the equation 92x^2+1=y^2.

Solution. The perfect square nearest to 92 is 10^2. This gives, from the relation 92 \times 1^2+8=10^2, a natural triple (1,10;8). Applying Brahmagupta’s bhāvanā on this starting triple, we get

\[
(1,10;8) \odot (1,10;8)= (20, 192; 8^2).
\]

Dividing the consequent identity 92 \times 20^2+ 8^2=192^2 by 8^2, one obtains the triple (\frac{5}{2}, 24; 1). Now

\[
\left(\frac{5}{2}, 24; 1\right) \odot \left(\frac{5}{2}, 24; 1\right) =(120, 1151;1),
\]

an integer triple. Thus, a solution to 92x^2+1=y^2 is given by x=120 and y=1151.

Note how Brahmagupta’s idea of playing with solutions of the more general equation 92x^2+z=y^2 helps in obtaining a solution of the specific equation 92x^2+1=y^2.

The thrill that Brahmagupta must have felt regarding bhāvanā can be imagined from a phrase he uses after stating the above problem: kurvannāvatsarād gaṇakạh, “One who can solve it within a year [is truly a] mathematician.”

Fixing z=1, equation \(\eqref{brahmaguptas-law}\) takes the form

\[\begin{equation}
(x_1,y_1) \odot (x_2,y_2)=(x_1y_2+x_2y_1, Nx_1x_2+y_1y_2). \label{brahma2}
\end{equation}\]

This rule shows, in particular, how to generate infinitely many, progressively larger, solutions of the equation Nx^2~+~1~=~y^2 from a given solution. As a simple illustration of its usefulness, see Box 2.

Box 2. Did Ramanujan use bhāvanā

The article by Sudhir Rao in this issue recalls a puzzle from The Strand Magazine which was mentioned by P.C. Mahalanobis to S. Ramanujan. To the surprise of Mahalanobis, Ramanujan gave the correct answer promptly and indicated that he obtained the solution through “continued fractions”—see Rao’s article for details.

The puzzle reduces to finding positive integers x,y such that

\[
2x^2+1=y^2 {\rm ~~ with ~~} 101 \le y \le 1001.
\]

Note that 2\cdot 2^2+1=3^2. Therefore, applying the bhāvanā [equation \(\eqref{brahma2}\)] for N=2 twice on the initial solution (2,3), we get immediately that (2,3) \odot (2,3)=(12,17) and (12,17) \odot (12, 17) =(408,577).

Thus, x=408,y=577 satisfies 2x^2+1=y^2 under the given constraint, and readily gives the solution to the original puzzle. The fractions \frac{3}{2}, \frac{17}{12} and \frac{577}{408} are respectively the second, fourth and eighth convergents of the continued fraction expansion of \sqrt{2}. How did Ramanujan arrive at the convergent \frac{577}{408} so fast? Did he use bhāvanā ?

As discussed in Rao’s article, being a convergent in the continued fraction expansion of \sqrt{2}, the solution (408, 577) of 2x^2+1=y^2 gives a very good rational approximation \frac{577}{408} (=1.414215\ldots) of \sqrt{2} (=1.414213\ldots), the best among all fractions whose denominators do not exceed 408. This approximation (matching the correct value up to 5 decimal places, 1.41421) was used by Vedic savants in a distant past and recorded by Baudhāyana (800 bce or earlier) and other authors of the Śulba-sūtras.

The solution (408,577) of 2x^2+1=y^2 appears to connect three great mathematicians from three different phases of Indian history (Vedic, Classical and modern).

Brahmagupta gives several remarkable results on integer solutions of Nx^2+1=y^2 which are all applications of his composition law \(\eqref{brahmaguptas-law}\); one of them is presented in Box 3 (see [2], pp. 90–95; ,[3] pp. 178–179 and [4]). 

Box 3. Application of bhāvanā: A theorem of Brahmagupta

Theorem (Brahmagupta). If Np^2-4=q^2, then x=pqr and y=(q^2+2)(r-1) satisfy the equation Nx^2+1=y^2, where r= \frac{1}{2}(q^2+3)(q^2+1).

The proof can be obtained by repeated application of the bhāvanā on the given triple (p,q; -4) and making necessary simplifications and adjustments; it is left as an exercise to the reader.

Example: For N=13, from the relation 13 \times 1^2-4=3^2, the above theorem produces the solution x=180, y=649 for 13x^2+1=y^2.

Using Brahmagupta’s bhāvanā and Āryabhaṭa’s kuṭṭaka, subsequent Indian algebraists developed a cyclic method called cakravāla which describes all integer solutions of Nx^2+1=y^2, for any arbitrary non-square positive integer N. (If N is a square, then it is easy to see that (0, \pm 1) are the only integer solutions.) The mathematician Jayadeva is the earliest known expositor of the cakravāla algorithm. He describes the problem of solving Nx^2+1=y^2 (in integers) as being as difficult as setting a fly against the wind!

Jayadeva’s verses on the cakravāla algorithm are quoted in the text Sundarī (1073) by Udayadivākara (see [5] for more details); we still do not know the dates of Jayadeva himself. Till any new evidence is found, we may regard Jayadeva as the first mathematician to have completely solved (in integers) the Brahmagupta–Pell equation Nx^2+1=y^2. In his treatise Bījagaṇita (1150), Bhāskarācārya gives a lucid exposition of a variant of Jayadeva’s method, illustrating it with difficult examples like N=61 and N=67. The bhāvanā and cakravāla are applied by Nārāyaṇa (c. 1350) to generate a sequence of progressively better rational approximations to the surd \sqrt{N}, when N is not a perfect square (see [6], pp. 670–672).

The cakravāla is a recursive algorithm on the solution space of Nx^2+z=y^2 to arrive at a solution with z=1. Note that (1,t, t^2-N) is a solution for every integer t. The cakravāla begins with the solution x_1=1, y_1=a and z_1=a^2-N, where a is a positive integer for which a^2 is closest to N. At every stage, it applies the bhāvanā to compose the solution (x_n,y_n,z_n) obtained at the n-th step with another solution (1,t_n, t_n^2-N) for a judiciously chosen t_n, to obtain (u_n, v_n, w_n), where u_n=x_nt_n+y_n, v_n=Nx_n+y_nt_n and w_n=z_n(t_n^2-N). The t_n is so chosen that z_n becomes a divisor of u_n (it follows that z_n would also divide v_n and t_n^2~-~N) and |t_n^2-N| is minimised among candidates satisfying the divisibility criterion. The (n+1)-th step is then defined to be the solution x_{n+1}=u_n/z_n, y_{n+1}=v_n/z_n, z_{n+1}=w_n/z_n^2. It can be shown that at some stage m, one would arrive at z_m=1. Box 4 illustrates the method through a famous example; the algorithm is discussed in the framework of continued fractions in [6]. 

Box 4. Application of bhāvanā-cakravāla: the case N=61

This problem was discussed by Bhāskarācārya (1150) and later posed by Fermat (1657).

As 64 is the square nearest to 61, we have the initial relation 61 \times 1^2+3=8^2, i.e., the triple (1,8;3). Applying bhāvanā between (1, 8;3) and (1,t; t^2-N), we get (8+t,~ 61+8t; ~~3(t^2-61)) and hence the relation 61 (\frac{8+t}{3})^2 + (\frac{t^2-61}{3})= (\frac{61+8t}{3})^2. The cakravāla prescribes choosing t such that (i) 3 divides (8+t) and (ii) |t^2-61| is the least.

The authors on cakravāla describe methods for determining such a t (using kuṭṭaka); here t is clearly 7. Thus, we have 61 \times 5^2-4 =39^2. Now, applying Brahmagupta’s theorem (see Box 3), we get the positive integral solution: x=226153980, y=1766319049.

One can see that Brahmagupta’s bhāvanā holds the key to the discovery of the cakravāla (cf. [2], pp. 95–99; [3], pp. 183–185). Jayadeva, Bhāskarācārya and subsequent authors make a detailed exposition of the bhāvanā just before describing the cakravāla. As Weil remarks ([7] , p. 22):

The term bhāvanā

When Manjul Bhargava first came to know of the name bhāvanā for Brahmagupta’s composition law, he exclaimed, “What a great word!” Indeed, the word bhāvanā has profound nuances. Its several meanings include “(finding by) composition or combination”, “creating”, “producing”, “generating”, “effecting”, “accomplishing”, “demonstrating”, “manifesting”, “conception”, “thought”, “reflection” and “contemplation”. It is also associated with the spiritual sense of “becoming (That)”—bhāva refers to a high spiritual state. In Upaniṣadic conception, the universe is a becoming (rather than a creation), a formative self-expansion of the One (the Eternal) manifesting its implicit Multiplicity. The word bhāvanā also connotes this conception of the One becoming the Many; the word bhava is often used in literature for the consequent manifestation: the terrestrial world!

Jayadeva mentions the term samāsa-bhāvanā (additive composition) for the equation \(\eqref{brahmaguptas-law}\) of Brahmagupta and viśeṣa-bhāvanā (subtractive composition) for the variant given by x_3=|x_1y_2 - x_2y_1|, y_3=|Nx_1x_2 - y_1y_2| and z_3= z_1z_2. While describing the roots obtained by his rule, Brahmagupta uses the word kṛtam (“accomplished”, “effected”), which is closely related to one of the meanings of bhāvanā. As many of the treatises of Indian algebraists between Brahmagupta and Jayadeva are no longer available, one does not know who first coined the term bhāvanā for Brahmagupta’s rule. But clearly the ancient Indian algebraists perceived it as a special multiplicative operation. For, the Sanskrit word bhāvita (usual meaning: “created”, “produced”; or “future”, “to be”) had already been adopted in Indian algebra by Brahmagupta and others to denote the product xy of different unknown quantities x,y. The choice of a similar word bhāvanā for Brahmagupta’s composition law alludes to the fact that the rule makes an insightful product of two triples (or pairs) of numbers. K.S. Shukla records ([5], p. 6) that, according to Udayadivākara, bhāvanā means “multiplication”. The word “multiplication” has two related associations: “composition” (or “product”) as also “generating (or becoming) many” and both apply to Brahmagupta’s bhāvanā. For, through the principle of composition [equation \(\eqref{brahma2}\)], infinitely many roots of Nx^2+1=y^2 emerge from one fundamental root, reminding one of the metaphysical bhāvanā, of the “One becoming Many”.

Thus, while the precise sense of bhāvanā for Brahmagupta’s rule is that of “composition” or “combination” (of roots), a sort-of generalised bhāvita (“product”), the term also carries the additional suggestion of being a principle of “creation”, “production”, “generation” of new roots (from given roots), of new results and of new concepts. In fact, it is mentioned by Datta-Singh ([4], p. 148) that bhāvanā also means a lemma or a theorem (which has been “demonstrated”, i.e., proved). And Brahmagupta’s bhāvanā is indeed an important theorem as well as a powerful lemma for “producing” other theorems. Further, the “conception” of bhāvanā is a result of deep “thought” and a theme for further “reflection” and “contemplation” (as it has the potential for “creating” new theories).

Just before stating the bhāvanā formulae, Jayadeva mentions ([5], p. 5): aśeṣakaraṇavyāpi bhāvanākaraṇa\ldots (“the bhāvanā pervades endless mathematical operations”). In the light of later developments, Jayadeva’s remark turns out to be prophetic. One wonders whether he knew of more applications of bhāvanā apart from cakravāla.

The naming of Brahmagupta’s rule by a strikingly appropriate word, rich in cultural significance, was clearly a tribute by an Indian savant to a very special discovery whose far-reaching importance was intuitively realised at that early stage.

Historical and mathematical significance of Brahmagupta’s bhāvanā

Brahmagupta was perhaps the first mathematician to have a clear vision of algebra as a distinct discipline in the form that we know it today. In his chapter Kuṭṭakādhyāyaḥ (628), Brahmagupta laid a firm foundation for the subject when he expounded on topics like the use of symbols for different unknowns, expansion of the number-system to include negative numbers and zero along with the ring-theoretic rules of operations over integers, operations with surds, formation of equations, the algebra of polynomials in several variables, solutions of linear and quadratic equations including the Gaussian method of elimination, and the kuṭṭaka method for finding integer solutions of the linear indeterminate equation ay-bx=c. The crest-jewel of this chapter on algebra is Brahmagupta’s treatment of the equation Nx^2+1=y^2 through bhāvanā. It is amazing that such an early treatise on classical algebra anticipates the concept of “binary composition” on abstractly defined elements, the quintessence of modern abstract algebra.

To appreciate the genius of Brahmagupta’s bhāvanā, we note that, apart from its beauty and technical power, the wizardry in classical algebra that is involved in its discovery at a formative stage of the subject, and its impact on subsequent research, the bhāvanā reveals an astonishingly modern attitude to an algebraic problem. For solving a problem in two variables, the bhāvanā is introduced to make a bold exploration of the solution space of a more general equation in three variables; and further, it acts on unknown (triples of) roots as if they are known numbers. In modern Europe, it is Lagrange who pioneered (c. 1770) the approach of investigating the general picture, and the study of actions on unknown quantities—both these features are now standard in modern algebra. Above all, Brahmagupta’s original idea of constructing a binary operation (and that too an intricate one) on unknown elements, and thus implicitly inventing an algebraic structure, is perhaps the first known instance of sophisticated abstract algebraic thinking. Modern algebra is dominated by the study of abstract structures like groups and rings; but it is only after a gap of eleven or twelve centuries from the time of Brahmagupta that the study, application and construction of such algebraic structures would be pursued in mathematics.

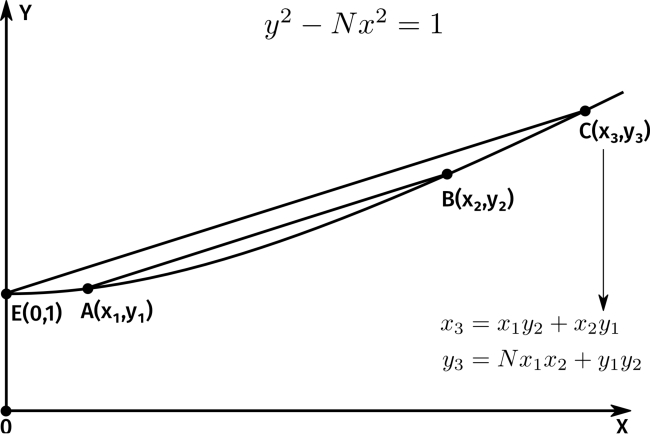
Using the clarity of the language of modern “Abstract Algebra”, Brahmagupta’s bhāvanā defines a binary operation on the set \{(x,y,z) \in {\mathbb Z}^3 ~|~Nx^2+z=y^2\} and a group structure on \{(x,y) \in {\mathbb Z}^2~|~Nx^2+1=y^2\} (or \{(x,y,z) \in {\mathbb Q}^3 ~|~Nx^2+z=y^2\}), where \mathbb Z denotes the set of integers and \mathbb Q the set of rational numbers. The group of integer solutions to Nx^2+1=y^2 is closely related to the group of units of a certain ring in algebraic number theory called the “ring of integers of the quadratic field {\mathbb Q}(\sqrt{N})”. The group structure on the conic y^2-Nx^2=1 defined by the bhāvanā [equation \(\eqref{brahma2}\)] has an elegant geometric interpretation (see figure): if A=(x_1,y_1) and B=(x_2,y_2) are points in the first coordinate on this conic, and C is the point where the line through the point E=(0,1) parallel to the chord AB meets the conic, then the coordinates of C are precisely (x_3,y_3) given by the bhāvanā [equation \(\eqref{brahma2}\)].¹

The discovery and application of composition laws on sets of significance is now a central theme of modern mathematics research. For instance, the “addition law” on the points of an elliptic curve is a basic tool in the study of the curve.

Brahmagupta’s bhāvanā [equation \(\eqref{brahmaguptas-law}\)] can be envisaged as the identity

combining two binary quadratic forms of the type x^2~-~Ny^2 to get another form of the same type. (Here, we interchange the role of x and y in equation \(\eqref{brahmaguptas-law}\) to match the standard notation in the theory of binary forms.) Among its many modern significances, the bhāvanā identity in equation \(\eqref{brahmaguptas-identity}\) is a statement of the multiplicativity of the “norm function”, a very important concept in modern algebra and number theory, and, of course, a principle of “composition” of binary quadratic forms.

The norm function || ~~ || associates to the expression x+\sqrt{N}y the integer obtained by multiplying x+\sqrt{N}y with its conjugate, i.e., ||x+\sqrt{N}y||=(x+\sqrt{N}y)(x-\sqrt{N}y)=x^2-Ny^2. It is an extension of the familiar device of associating, to a complex number a+ib, the real number (a+ib)(a-ib)=a^2+b^2. Brahmagupta’s identity [equation \(\eqref{brahmaguptas-identity}\)] can thus be reformulated as the statement ||\alpha||||\beta||=||\alpha\beta||, for numbers of the form \alpha =x+\sqrt{N}y (see [2], pp. 82–84 and 100–101 for more details).

The immense potential of the bhāvanā identity came to be harnessed after its appearance in Euler’s writings; it is now a basic result used repeatedly in modern number theory (reminding one of Jayadeva’s remark). For instance, Brahmagupta’s identity is a crucial ingredient in one of the main theorems of Legendre (1785) which leads to an important local-global theorem in number theory pertaining to the existence of nonzero integer solutions of ax^2+by^2=cz^2, where a,b,c are positive integers with abc square-free. The bhāvanā is also involved in the Lorentz transformation in the theory of relativity. ²

A version of the bhāvanā identity was generalised in 1965 by A. Pfister using, what are now called, “Pfister forms”. Pfister’s discovery opened up new directions in the theory of quadratic forms, an account of which is presented by Manuel Ojanguren in Chapter 5 of his monograph [8]. The chapter begins by quoting Brahmagupta’s original Sanskrit verses on the bhāvanā and is titled Also sprach Brahmagupta³

Gauss’s Composition Law

The importance of the equation Nx^2+1=y^2, when N is a non-square positive integer, was later recognised in modern Europe. Pierre de Fermat, who wanted contemporary mathematicians to take serious interest in number theory, posed (in 1657) the problem of finding infinitely many integer solutions to the above equation (see Box 5). Fermat’s intense involvement, and his success in drawing the attention of other mathematicians to such number-theoretic questions, heralded the advent of modern number theory. 

Box 5. Excerpts from Fermat’s letter to English mathematicians

“There is hardly anyone who proposes purely arithmetical questions, hardly anyone who understands them. Is this due to the fact that up to now arithmetic has been treated geometrically rather than arithmetically? This has indeed been the case both in ancient and modern works; even Diophantus is an instance. For, although he has freed himself from geometry a little more than others have in that he confines his analysis to the consideration of rational numbers, …

Now arithmetic has, so to speak, a special domain of its own, the theory of integral numbers. This was only lightly touched upon by Euclid in his Elements, and was not sufficiently studied by those who followed him …; arithmeticians have therefore now to develop it or restore it.

To arithmeticians therefore, by way of lighting up the road to be followed, I propose the following theorem to be proved or problem to be solved. If they succeed in discovering the proof or solution, they will admit that questions of this kind are not inferior to the more celebrated questions in geometry in respect of beauty, difficulty or method of proof.

Given any number whatever which is not a square, there are also given an infinite number of squares such that, if the square is multiplied into the given number and unity is added to the product, the result is a square.”

A vigorous investigation was launched on the equation by several leading mathematicians including Brouncker and Wallis in the seventeenth, and Euler and Lagrange in the eighteenth, centuries; the equation somehow acquired the name “Pell’s equation”. Research on the Brahmagupta–Pell equation went on to become a part of more general theories developed by some of the best mathematical minds of modern Europe. One of the fruitful theories to emerge was the theory of binary quadratic forms (with integer coefficients), systematically developed by Lagrange and Legendre after initial contributions from Fermat and Euler.

A big advancement on the theory of binary quadratic forms was made by C.F. Gauss in his Disquisitiones Arithmeticae (1801) when he constructed a composition law on general binary quadratic forms of a given discriminant, i.e., it composes two expressions a_1x_1^2+b_1x_1y_1+c_1y_1^2 and a_2x_2^2+b_2x_2y_2+c_2y_2^2 with b_1^2-4a_1c_1=b_2^2-4a_2c_2=D (say) to produce an expression a_3x_3^2+b_3x_3y_3+c_3y_3^2 with b_3^2-4a_3c_3=D.

The result of Gauss actually says much more. Call two (integral) binary forms Q_1(x,y) and Q_2(x,y) with the same discriminant D to be “equivalent” if there exist integers p,q,r,s with ps-qr=1 such that Q_2(x,y)=Q_1(px+qy,rx+sy), i.e., if Q_2 can be obtained from Q_1 by a certain homogeneous linear change of variables; and call a binary quadratic form ax^2+bxy +cy^2 to be “primitive” if the integers a,b,c do not have any common prime factor. Gauss showed that there are only finitely many equivalence classes of primitive binary quadratic forms with discriminant D. In the later language of abstract algebra, his composition law imparts to the set of equivalence classes of primitive binary quadratic forms the structure of a finite Abelian group. This result was accomplished by Gauss several decades before the concept of an abstract group emerged formally during the second half of the nineteenth century. It is considered to be one of his deepest discoveries.

Gauss’s composition had not only a profound influence on classical number theory, it paved the way for ideal theory and modern algebraic number theory whose foundations were eventually laid in an elegant form by R. Dedekind (c. 1871). It was the first major attempt to address the nonuniqueness of factorization in certain extensions of \mathbb Z. (This nonuniqueness has been the stumbling block in the quest for a valid proof of “Fermat’s Last Theorem” through elementary number theory.)

By a work of Dirichlet (1838), the group that was implicit in Gauss’s work was shown to be isomorphic to the “oriented (or narrow) ideal class group” of the quadratic number field {\mathbb Q}(\sqrt{D}). The ideal class group, that was formulated by Dedekind refining the work of Kummer, is a measure of the extent to which uniqueness of factorisation of elements fails in the ring of integers of {\mathbb Q} (\sqrt{D}). Again, based on ideas implicit in Gauss’s work, Minkowski developed the “geometry of numbers” (1896) which reduces various number theory problems to counting lattice points in appropriate regions.

Bhargava’s Composition Law

For 200 years, Gauss’s composition law appeared to be an isolated curiosity peculiar to binary quadratic forms and no one had any hunch that there could be other composition laws for polynomials of higher degree. To the pleasant surprise of mathematicians, Manjul Bhargava has now introduced (2001) a completely new way of looking at the principle of composition which gives an insightful and simpler presentation of the classical Gauss composition and reveals thirteen new laws of composition for higher degree polynomials. Bhargava has also developed powerful methods in the geometry of numbers. Applying his composition laws and his new tools in the geometry of numbers, Bhargava made breakthroughs in some of the fundamental open problems of number theory.

One of the central problems in number theory is to obtain an asymptotic formula for the number of number fields of a fixed degree n with bounded discriminant (i.e., the absolute value of the discriminant is less than a fixed number D). Progress on this question had stopped after Davenport and Heilbronn solved the case n=3 in 1971. Bhargava applied his new methods to solve the cases n=4 and n=5.

Another problem pertains to finding or counting the number of points with rational coordinates satisfying the hyperelliptic curve y^2=f(x), where f(x) is a polynomial of degree n with rational coefficients having n distinct roots. This is a generalisation of ancient problems like the Brahmagupta–Pell equation (where f(x)=Nx^2+1 and the curve has infinitely many rational solutions). The case n=3 is that of the elliptic curve which has been a subject of much research and has played an important role in Andrew Wiles’s proof of Fermat’s Last Theorem. Bhargava and his collaborators have obtained striking results on elliptic and hyperelliptic curves. For instance, Bhargava showed that when n \ge 6, most (in a precise sense) hyperelliptic curves do not have rational solutions.

The highly technical accomplishments of Bhargava have their genesis in an inspired idea coming from his contemplations on a cube (Rubik’s cube). Given a cube with integers a, b, c, d, e, f, g, h attached to the eight vertices,

Bhargava associates with them the six 2 \times 2 matrices given by the six faces:

M_1=\left( \begin{array}{cc} a&b \\ c&d \end{array} \right),~M_2=\left( \begin{array}{cc} a&c \\ e&g \end{array}\right),~M_3=\left( \begin{array}{cc} a&e \\ b&f \end{array} \right) and N_1=\left( \begin{array}{cc} e&f \\ g&h \end{array} \right),~N_2=\left( \begin{array}{cc} b&d \\ f&h \end{array} \right), ~N_3=\left( \begin{array}{cc} c&g \\ d&h \end{array} \right).

He uses the six matrices to define three quadratic forms Q_1, Q_2, Q_3 by

\[Q_i(x,y)= -{\rm Det}~(M_ix+N_iy), ~~1\le i \le 3.\]

For instance, Q_1(x,y)=-(ax+ey)(dx+hy)+(bx+fy)(cx+gy).

It can be verified that the three forms Q_1,Q_2,Q_3 have the same discriminant. In case the forms are primitive, Bhargava observes that -Q_3 is equivalent to the “product” of Q_1 and Q_2 defined by Gauss’s composition.

Conversely, Bhargava shows that any three primitive binary quadratic forms Q_1,Q_2 and Q_3, with -Q_3 equivalent to the Gauss composition of Q_1 and Q_2, arise as above from an integral cube, now called “Bhargava’s cube”.

The following simple and elegant example of Bhargava’s cube

defines the quadratic forms Q_i(x,y)=x^2-Ny^2 for each i, 1 \le i \le 3, and thus represents Brahmagupta’s bhāvanā.

Epilogue

The Sanskrit meanings of the word gupta include “protected” and “preserved” as well as “hidden” and “secret”. While the name Brahmagupta literally means “protected by Brahma”, the genius of Brahmagupta has hitherto remained “hidden” from modern students of mathematics and history and, of course, from the general public. With the sensational discoveries of Bhargava, and the connection between an important aspect of his works and an important contribution of Brahmagupta, there is now a possibility that the legacy of the genius would no longer remain a forgotten “secret”; rather, it may be “preserved”.

While receiving the Cole Prize (2008), Manjul Bhargava acknowledged, after the citation:

One may recall the dates of the works of the mathematicians in the first list: Brahmagupta (628), Gauss (1801), Dirichlet (1838), Eisenstein (1844) and Dedekind (1871).

The word bhāvanā brings to our mind a brilliant mathematical concept from a bygone era along with its sublime spirituo-cultural ambience. It also provides a link between one of the highest peaks of ancient Indian mathematics and one of the most celebrated achievements in contemporary mathematics. May it inspire more and more profound bhāvanā in future!

acknowledgements The author thanks Manjul Bhargava, Raja Sridharan, Avinash Sathaye, C.S. Rajan, C.S. Aravinda, V. Balaji and Prithwindra Mukherjee for valuable suggestions and stimulating discussions on the theme.

References

• [1] A.K. Dutta, Bhāvanā from Brahmagupta to Bhargava, under preparation.
• [2] A.K. Dutta, Brahmagupta’s Bhāvanā, Contributions to the History of Indian Mathematics (ed. G.G. Emch, R. Sridharan, M.D. Srinivas), Hindustan Book Agency, New Delhi (2005), pp. 77–114.
• [3] A.K. Dutta, Kuṭṭaka, Bhāvanā and Cakravāla, Studies in the History of Indian Mathematics (ed. C.S. Seshadri), Hindustan Book Agency, New Delhi (2010), pp. 145–199.
• [4] B. Datta and A.N. Singh, History of Hindu Mathematics Part II, Motilal Banarasidass (1938); reprinted by Asia Publishing House (1962) and Bharatiya Kala Prakashan (2004).
• [5] K.S. Shukla, Ācārya Jayadeva, The Mathematician, Gaṇita 5 (1954), pp. 1–20.
• [6] A.K. Dutta, Nārāyaṇa’s treatment of varga-prakṛti, Indian J. History of Science 47.4} (2012), pp. 633–677.
• [7] A. Weil, Number Theory: An Approach through History from Hammurapi to Legendre, Birkhauser (1984).
• [8] Manuel Ojanguren, The Witt Group and The Problem of Lüroth, Dottorato di ricerca in Matematica, ETS EDITRICE PISA, University of Pisa (1990).
• [9] Brāhma-sphuṭa-siddhānta (628). Printed versions have been edited and published by S. Dvivedi, Varanasi (1902) and R.S. Sharma, Indian Institute of Astronomical Research (1966).
• [10] C.F. Gauss, Disquisitiones Arithmeticae (1801).
• [11] M. Bhargava, Higher Composition Laws and Applications, Proceedings of the International Congress of Mathematicians, Madrid (2006), pp. 271–294.
• [12] L.E. Dickson, History of the Theory of Numbers Vol II, Carnegie Institute Publ. 256 (1920), reprinted by Chelsea Publishing Co. NY (1952) and AMS Chelsea (1999).

Footnotes

1. To see this, note that the equation for the line EC is y-1=mx, where m=(y_2-y_1)/(x_2-x_1). Hence if C=(u,v), then (1+mu)^2-Nu^2=1, giving u=a/b, where a=2(y_2-y_1)(x_2-x_1) and b=N(x_2-x_1)^2-(y_2-y_1)^2=2(y_1y_2-Nx_1x_2-1). Now, setting x_3=x_1y_2+x_2y_1 (as prescribed by bhāvanā), one can verify that x_3b=a, showing that u=x_3.↩
2. A special case of the identity in equation \(\eqref{brahmaguptas-identity}\) is (a^2-b^2)(x^2-t^2)={x^{\prime}}^2-{t^{\prime}}^2, where x^{\prime}=ax+bt, y^{\prime}=at+bx. Now setting k=1/\sqrt{1-v^2}, a=k, b=-kv, the expressions for x^{\prime}, y^{\prime} are precisely the Lorentz transformation which keeps the form x^2-t^2 invariant, i.e., x^2-t^2={x^{\prime}}^2-{t^{\prime}}^2. (See “A simple non-Euclidean geometry and its physical basis” by I.M. Yaglom, p. 167.)↩
3. In English: “Thus spake Brahmagupta”.↩