Timeless Geniuses, Celestial Clocks and Continued Fractions

Continued fractions, is an idea that is at once not only simple, but also one which holds within its infinite recursive folds and recesses many secrets and surprises. Perhaps dating back to remote antiquity, yet fully vigorous even today, it stands as a testament to a paradigm that is well known to mathematicians, which is that an idea may be old, but is never ruled out as having fully exhausted its possibilities. A common theme that binds the uncommon stories presented in this article is the omnipresent yet almost reticent continued fraction.

Ramanujan, Mahalanobis and The Strand Magazine

The name Srinivasa Ramanujan often invokes strong emotions in mathematicians, particularly if they happened to have worked in an area that Ramanujan’s short and incredibly romantic life (romantic only in the sense of the intensity of its pathos), touched and impacted. His name, for everybody else, learned and lay, is synonymous with an attribute that can only be called Genius. Timeless Genius.

Such reputations are of course earned. An incident that serves to burnish Ramanujan’s reputation as a man who had free access to spaces and planes of the human mind that are only dreamt of, but never realized, by most of humanity, is vividly narrated (pages 214–215) in the book The Man Who Knew Infinity by Robert Kanigel—the book that inspired the recent Hollywood movie with the same title.

The story goes as follows. The Strand Magazine, a local London publication, used to run a regular column called “Perplexities”. In the December of 1914, this column featured a puzzle titled “Puzzles at a Village Inn”, which an Indian student then in Cambridge, Prasanta Chandra Mahalanobis, brought to the attention of his friend and compatriot, Ramanujan. The puzzle:

Mahalanobis is supposed to have figured this out in a few minutes by a trial and error method. He then posed the puzzle to Ramanujan, who was cooking a meal when he heard this question. Much to his friend’s surprise, who did not have to wait long, Ramanujan asked him to take down the solution. Amazed at the spontaneous answer, Mahalanobis asked him how he did it: Ramanujan says that as soon as he heard the problem, he knew that there should be a continued fraction; and that when he asked himself which one it was, the answer apparently just came to his mind!

So, what is a continued fraction? And what could Ramanujan’s solution have been?

Let us first embark on a brief journey of the continued fractions. One normally learns to express real numbers, both rationals and irrationals, in their decimal expansions, that is, writing \frac{1}{2} as 0.5 and such. That is why one also tries to express the number \pi, an irrational, as 3.1415\ldots and approximate it to monstrously large decimal places but, alas, there appears to be no discernible pattern in the digits of the expansion. In this article, however, we discuss another way, perhaps a more elegant and fruitful way, of representing real numbers as “generalized” fractions, or what are mathematically known as continued fractions. Here are a few elementary examples:

1. Any integer, say -10, written as a quotient is simply \frac{-10}{1}; so we need not do anything to express it as a continued fraction and leave it as -10.
2. Consider the rational number \frac{22}{7}, which we could rewrite as \[\cfrac{22}{7}= 3 + \cfrac{1}{7}\,.\]
3. Now, take another rational number, say, \frac{72}{28}, and write it as
\[\begin{aligned}\frac{72}{28} &= 2 + \frac{16}{28} &=2~~~+~~~~\cfrac{1}{\frac{28}{16}} &= 2 + \cfrac{1}{1 + \frac{12}{16}} \\&= 2 + \cfrac{1}{1 + \frac{3}{4}} &= 2 + \cfrac{1}{1 + \cfrac{1}{\frac{4}{3}}} &= 2 + \cfrac{1}{1 + \cfrac{1}{1 + \frac{1}{3}}}\,.\end{aligned}\]
4. Let us repeat the above procedure with another rational number, say, \frac{176}{31}:

Looking at the examples above, one may be reminded of Euclid’s algorithm to find the greatest common divisor, or GCD, of any two given numbers, a procedure which involves many ideas similar to the continued fraction representation of a number.

In general, an expression of the form
\[a_0 + \cfrac{b_1}{a_1 + \cfrac{b_2}{a_2 + \ddots}}\]

where the a_i and b_i are integers, is called a continued fraction. When the b_i are all equal to 1 and a_i for i\geq1 are all natural numbers, as in the examples above, we call it a simple continued fraction, or SCF.

Now, an obvious question to pose is: Can irrationals also be represented using continued fractions? The answer is yes but with a crucial difference—the continued fraction representations for rationals terminate after finitely many steps, whereas for the irrationals, the process does not end.

Here is a classic example of what we are talking about. What could the number x below be?

Since the fractional part continues indefinitely, one can observe that the expression in the denominator of the second term on the right-hand side of the equation is actually the same as x itself! Strange indeed, but it is true! Mathematically, this amounts to the fact that x satisfies the equation x=1+\frac{1}{x}; or equivalently, x^2-x-1=0. The positive root of this equation is the ubiquitous golden ratio, usually denoted as \Phi, and is equal to (1+\sqrt{5})/2.

The term “golden ratio” comes from a special property: It is a ratio of two numbers that equal the ratio of their sum to the larger of the two numbers. That is, if a,b are two numbers such that a > b > 0, then \Phi=a/b=(a+b)/a; in other words, \Phi=a/b satisfies x=1+\frac{1}{x}. In the case of the golden ratio, we obtained a quadratic equation in x from the continued fraction representation of x.

This process can be run in reverse, i.e., one can obtain the continued fraction representation of a number from a quadratic equation. Quadratic equations can also be used to build a continued fraction representation. For example, \sqrt{2}, one of the earliest irrationals to be discovered, can be thought of as a root of the quadratic equation x^2-2=0. This can be rewritten as

x=1+\frac{1}{x+1}.
Now, simply replace the x on the right-hand side by the expression 1+\frac{1}{x+1}, which is the same as x according to the left-hand side of the above equation. This yields

By continuing this process recursively, we see that

\[x=1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \ddots}}}\]

In other words, we have just obtained a simple continued fraction expansion of \sqrt{2}. Numbers such as \sqrt{2} fall into the category of quadratic irrationals, which are irrational numbers that are solutions to the quadratic equation ax^2 + bx + c = 0, where a,b,c are rational numbers with a \neq 0. Simple continued fraction expansions exist not only for quadratic irrationals but for every real number, including \pi and e.

Of course, the simple continued fraction expansions of such irrationals contain an infinite number of terms, unlike those of rational numbers, which contain finitely many terms. However, finite could still mean a large number, depending on the rational number in question. Much like how one writes only a few decimal places of a real number, the SCF representation of any real number can be truncated at different stages, which yields rational numbers called convergents. For example, \frac{1}{1}, \frac{2}{1}, \frac{3}{2}, \frac{5}{3} and \frac{8}{5} are the first five convergents of the SCF for the golden ratio \Phi described earlier.

Convergents provide good approximations of real numbers. One aspect of approximating irrational numbers by rational fractions involves determining which of the fractions, differing from the given irrational within a specified degree of proximity, has the largest denominator. Such approximations are meaningful even for rational numbers—if a rational number has an extremely large numerator and denominator, one may want to approximate it by another rational number whose numerator and denominator are smaller.

Mathematically, a rational number a/b is a best approximation of a real number \alpha if \vert \alpha - a/b\vert < \vert \alpha - c/d\vert for rationals c/d with 0<d\leq b and c/d \neq a/b.

With regard to SCF representations of real numbers, it turns out that the later you truncate an SCF, the better the approximation you get. Let us denote the rational number obtained by truncating an SCF at the n-th stage as p_n/q_n; let this also be the best approximation of a real number \alpha. Therefore, the n-th convergent p_n/q_n in the SCF of \alpha is the best possible rational approximation that is closest to \alpha among all rational numbers with denominators less than or equal to q_n. (For more on the delightful topic of continued fractions, see [6] and [8].)

Now, back to the Ramanujan–Mahalanobis story: Let us assume that the total number of houses on the particular Louvain street is m and that the number of the particular sought-after-house is n. The problem in The Strand Magazine, stated in mathematical terms, means that 1+2+3+\cdots+(n-1)=(n+1)+\cdots+m. Working out the two sums (using high school algebra), one gets the relation

or, equivalently,

Even more conveniently expressed, the equation to be solved in integers is x^2-2y^ 2=1, for x=2m+1 and y=2n, which is a particular case of the so-called Pell’s equation, or what is now called the Brahmagupta–Pell equation. (For more on this, see the article The bhavana in Mathematics)

How does one go about solving such an equation? The answer is that some of the convergents of the continued fraction for \sqrt{2} provide solutions to the above equation. Let us try to elaborate a bit on this point.

The interesting case of the general Brahmagupta–Pell equation x^2-dy^2=1 occurs when the integer d is a not a square. For, if d=r^2 for some r, then the equation x-dy^2=1 can be written as (x+ry)(x-ry)=1, which is possible if and only if (x+ry)=(x-ry)=\pm1. Therefore, x=\frac{(x+ry)+(x-ry)}{2}=\pm1. This means that x=\pm1 and y=0 are the only solutions.

Therefore, non-trivial solutions of the equation x^2-dy^2=1 exist only when d is a non-square positive integer, such as d=2. It turns out that if p and q are positive solutions of the equation, then p/q is a convergent of the SCF expansion of \sqrt{d}. Although not all convergents provide solutions, some of the convergents do. We can see this for d=2.

The convergents obtained by truncating the continued fraction for \sqrt{2} after the first few successive terms are

The pairs (x,y)=(1,1), (3,2), (7,5), (17,12),\ldots alternately satisfy x^2-2y^2=-1 and x^2-2y^2=1. In fact, the solution x=2m+1=17 and y=2n=12 gives m=8 and n=6, which is one of the solutions described in Robert Kanigel’s book.

For The Strand Magazine puzzle, one has to find an integer m between 50 and 500 and an integer n satisfying (2m+1)^2-2(2n)^2=1. We shall now use the theory of SCF to show that m=288 and n=204 is the only solution, i.e., the number of the sought-after house is 204. Working through the successive convergents of the SCF expansion of \sqrt{2} after (17,12), one gets (41,29), (99,70), (239,169), (577,408),(1393,985), (3363,2378),\ldots as solutions, alternately, to x^2-2y^2=-1 and x^2-2y^2=1. Thus, the solutions to x^2-2y^2=1 are given by (3,2), (17,12), (99,70), (577, 408), (3363, 2378),\ldots. Now finding m such that 50 \le m \le 500 amounts to looking for x\,(=2m+1) such that 101 \le x \le 1001. Thus, it becomes clear that x=577 and y=408 is the unique solution to x^2-2y^2=1 under the constraint that x lies between 101 and 1001. Hence n\,(=y/2)=204 (with m=288) is the unique solution to the puzzle.

The particular convergent \frac{577}{408}, corresponding to m=288 and n=204, is obtained by truncating the SCF at the eighth step. Note that the previous and the next solutions of x^2-2y^2=1 are (99,70) and (3363,2378) giving m=49, n=35 and m=1681, n=1189 respectively, which are, of course, outside the specification in the puzzle which stated that there were more than 50 houses on the street but not more than 500.

Curiously enough, the fraction \frac{577}{408} which solves The Strand Magazine puzzle has another Indian connection, and takes us back to anonymous ancient Indian mathematicians. The mystic seers of the Vedic Age had made many remarkable mathematical discoveries and innovations. Some of their knowledge, especially those results in geometry and arithmetic which are needed for building the vedis or altars, are preserved in later treatises called Śulbasūtras which, though composed much after the Vedas, still belong to a pre-historic period (800 BCE or earlier).

Baudhāyana, Āpastamba and Kātyāyana are the three most prominent authors of the Śulbasūtras, which describe both exact geometric constructions of irrational numbers like \sqrt{2}, as well as their rational approximations (see [1] (section 5) and [2] for a detailed discussion). One of the rational approximations for \sqrt{2} that the Śulbasūtra authors record is the following sum of unit fractions:

And what is the expression for this number as a single rational number p/q? It is again \frac{577}{408}, the eighth convergent p_8/q_8 in the SCF expansion for \sqrt{2}. The very convergent from Ramanujan’s prompt answer, while cooking a meal, to Mahalanobis’s question!

Śulbasūtra authors also give the rational approximations \frac{7}{5} and \frac{17}{12} for \sqrt{2}, i.e., the third convergent p_3/q_3 and fourth convergent p_4/q_4; indeed, 1+\frac{1}{3}+\frac{1}{3\cdot4}=\frac{17}{12}. Thus, each of these (rational) approximations for \sqrt{2} is really the best possible in a precise sense as elaborated above—they are the best among all fractions with denominators not exceeding the denominator of the chosen rational approximation.

The Archimedes Cattle Problem

Continued fractions and the Brahmagupta–Pell equation also make their appearance in another interesting problem, posed by Archimedes and presented as a challenge to his peers in Alexandria.

It was sent in a letter to Eratosthenes of Cyrene—now at least 2,200 years old—and is scripted in beautiful verse. In the mathematical world, it is called the Archimedes Cattle Problem because it involves a certain definite number of bulls and cows. The bulls are of four different types, as are the cows. The problem posed in verse is a series of constraints that the variables are subjected to.

Assuming that the four “bull” variables are x, y, z, and t, and their “cow” counterparts are a, b, c and d, the equations read as follows:

The problem challenges people to find the size of the herd (a+b+c+d+x+y+z+t), and also to find out how many bulls and cows belong to each of the four respective varieties.

Archimedes stated that a person who could “merely” solve this portion of the problem was at best competent. He then suggested two more constraints that had to be satisfied by the solution of these equations [9]:

“… But come, understand also all these conditions regarding the cattle of the Sun. When the white bulls [x] mingled their number with the black [y], they stood firm, equal in depth and breadth, and the plains of Thrinacia, stretching far in all ways, were filled with their multitude. Again, when the yellow [z] and the dappled bulls [t] were gathered into one herd they stood in such a manner that their number, beginning from one, grew slowly greater till it completed a triangular figure, there being no bulls of other colours in their midst nor none of them lacking…”

In mathematical terms, x + y had to be a square; i.e., x+y=r^2 for some r. Also, z+t had to be a triangular number; i.e., z+t=n(n+1)/2 for some n. The one who solved this harder version could stake claim to the prize of supreme wisdom [9]:

“If thou art able, O stranger, to find out all these things and gather them together in your mind, giving all the relations, thou shalt depart crowned with glory and knowing that thou hast been adjudged perfect in this species of wisdom.” 

What is “Triangular” about Numbers of the Form n(n + 1)/2?

One learns in high schools that 1+2+\cdots+n=n(n+1)/2. One may also have heard the story of Gauss’s childhood exploit where he stumped his school teacher by arriving at the above formula on the spot. The evaluation of the same sum relates to another anecdote (see [5]) that demonstrates the precocious mathematical prowess of a 20th century mathematician.

William Thurston, Jr. (1946–2012) was famous for his unusually fertile imagination, coupled with powerful geometric insights. He went on to make major contributions to the world of geometry, and his work was recognized with a Fields Medal in 1982.

We recall an incident that transpired when Thurston was still a little boy, which led his father, Paul, to discover young Thurston’s innate ability to summon at will original mathematical ideas. His father, a physicist, used to ask young William and his siblings questions from elementary school mathematics. Below is a conversation between Paul Thurston and William:

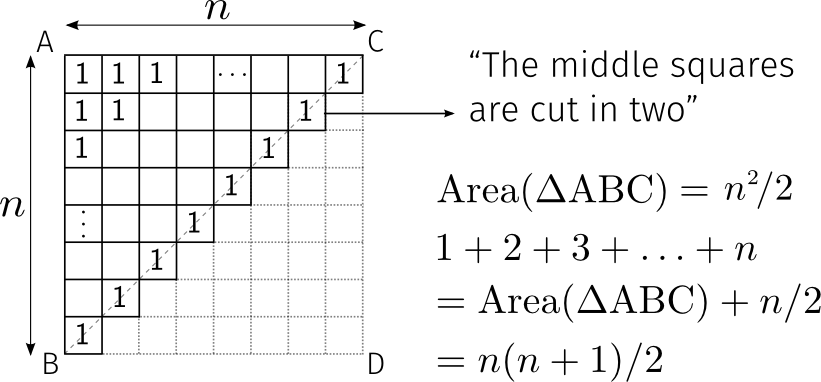
Paul: “What is 1 + 2 + \cdots + 100?”

Bill said, “5,000.”

Paul said, “Almost right.”

Bill said, “Oh, I filled one square with 1, two squares for 2 and all the way up to 100, so that’s half of 100 \times 100 = 10,000, but I forgot that the middle squares are cut in two, so that’s 5,050!”

Once these additional constraints are imposed, the solutions to the cattle problem grow to monstrously large numbers whose digits take up 47 pages if completely written out. Regarding the size of these solutions, David Fowler, a historian of Greek mathematics said “I don’t know what anybody would do with a solution, once found, except use it as a piece of mathematical wallpaper!” (see [10])

We will briefly sketch the key ideas involved in solving the problem. The continued fractions appear as a means to ensure that the solutions satisfy the triangular number constraint.

We begin midway through the solution process by considering the set

S_1= \left\lbrace 1, \frac{y}{x}, \frac{z}{x}, \frac{t}{x}, \frac{a}{x}, \frac{b}{x}, \frac{c}{x}, \frac{d}{x} \right\rbrace

that involves the variables in the Cattle Problem. It can be shown that the set

helps solve the cattle problem. Since the solutions must be integers, we multiply each number in this set by the LCM of all its members, which is x = 10366482. We then get

as the set that gives the smallest integral solution to the cattle problem, with each member of the set representing x,y,z,t,a,b,c,d respectively. But this solution does not satisfy the two additional constraints—that x+y must be square and z+t must be triangular—imposed by Archimedes. As we will see, the solutions start to grow in size as these two constraints are enforced one by one.

The square constraint on x+y means that

is supposed to be a square. The prime factors of 17826996 are 2^2, 3, 11, 29 and 4657. Removing 2^2, and retaining the rest of the terms, we require g=(3\cdot11\cdot29\cdot4657)f to be a square. Therefore f = 3\cdot11\cdot29\cdot4657\,m^2 = 4456749\,m^2, for some integer m, will make g a square number. Multiplying each element of the set S_2 with 4456749\,m^2 constitutes a solution set that satisfies the square constraint:

We will now impose the triangular number constraint on z+t, which requires that

for some n. That is, we are looking for an integer solution, for n, of the quadratic equation

which happens exactly when the discriminant 1 + (4 \cdot 2 \cdot 51285802909803)m^2 is a square. This implies that the statement above is true only if 1 + 410286423278424 \,m^2 =k^2 for some k. This is again another case of the Brahmagupta–Pell equation x^2 - dy^2 = 1, but with a very large value of d.

While it is not clear who in ancient Greece laid claim to the basic prize for solving the Cattle Problem, let alone the one for supreme wisdom, this problem gained traction in modern times. In 1867, C.F. Meyer, a German mathematician, set out looking for the solution using a continued fraction expansion of \sqrt{410286423278424}. He toiled through 240 steps of the continued fraction expansion, and gave up [7].

In 1880, A. Amthor solved the problem, using a different approach from continued fractions, and presented intriguing numbers. The smallest number—there are infinitely many solutions—was 7.766 \times 10^{206544} cattle.

Note that in the Archimedes cattle problem, it is given that the number of solutions had to be integers—a fractional or even rational number of cattle would clearly not make much sense, except of course, to a butcher!

Ultimately, C.F. Meyer’s attempted use of continued fractions in solving the cattle problem may seem a mere abstract curiosity to many. However, there was one event that occurred centuries ago that still touches our lives, and lends a measure of stability to our sense of the passage of time. It is an event that makes sense, in hindsight, through the lens of continued fractions.

Centurial Years—To Leap or Not to Leap?

In October 1582, Pope Gregory XIII introduced a new calendar that was a refinement of the Julian calendar in use until then. The correction introduced in what became known as the Gregorian calendar was minimal, in the sense that it shortened the mean length of the calendar year from 365.25 days to 365.24219878 days, which is a change of 0.002\%. Thus, for all practical purposes of calculating the length of the year, the change is minimal.

The motivation for the Church to make this change, however, was a more dire one. In the Julian calendar, the number of calendar days between the celebration of Easter and the occurrence of the spring equinox¹ seemed to drift, i.e., increase over time. The Church had always identified the two together, and the fact that the equinox and Easter fell on different days didn’t exactly please the Church, intent as it was on the symbolism and significance of long held beliefs. In the Indian context, an analogous situation would have been that of our own Makara Sankranthi coinciding with, say, either Christmas, or our Republic Day.

At the heart of the effected change of 0.002\% in the mean length of the calendar year was the change in leap years. Under the Julian system, centurial years that are divisible by four were leap years. This included every centurial year such as 2100, 2200, \ldots. Under the Gregorian system, however, centurial years such as 2100, 2200, 2300 will not be leap years, but 2400 and 2800 would qualify. In general, any centurial year that was an integer multiple of 400 was a leap year. But why?

Let us call a block of q years in which there are p leap years (p < q) as a cycle. The job of refining the calendar now involves coming out with an easy and efficient way of finding q and p such that, according to the Gregorian calendar’s predictions, Easter and spring equinox are always on the same day. In every cycle, there will be a total number of (365\,q + p) days. Therefore, every mean year will be (365 + p/q) days long. The challenge is to make this quantity, p/q, as close as possible to the day length in excess of 365, as per the new Gregorian calendar. We know that this number is 0.24219878.

Enter continued fractions. The first few convergents in the SCF expansion of 0.24219878 turn out to be \frac{1}{4}, \frac{7}{29}, \frac{8}{33}, \frac{31}{128}, \frac{163}{673}. The first fraction corresponds to the Julian system of one leap year every 4 years. But this is precisely the system that caused the problem we wanted to fix in the first place. The next convergents offer cycle lengths of 29, 33, 128 and 673 years, which are not very convenient. But is there a way out?

If 0.24219878 was multiplied by 100, we get 24.219878 whose SCF has \frac{97}{4}, \frac{121}{5}, \frac{218}{9} and \frac{993}{41} as the first few convergents. Since the denominator is the cycle length, one has to multiply 4 with 100, giving a 400-year cycle. This is the key step. Is there a way to match the excess of 24.219878 days with a 400-year cycle?

The very first convergent has the answer: 97 leap years in 400 years. Can one work with these numbers? Yes, if we mandate that only the centurial year divisible by 400 will be a leap year. Everything dramatically falls into place. 2000, 2400, 2800 will all be leap years, while 2100, 2200, 2300 will not be leap years according to the changed canon. While there is no evidence that continued fractions were the method through which the Gregorian calendar was made, there is a curious twist of history here—Greece, the land of Archimedes and the Cattle Problem, was one of the last European countries to adopt the changed calendar!

For millenia, the repeated appearance of continued fractions in seemingly unconnected stories sampled in this article have enthralled us on issues ranging from counting cattle to something as mundane as a calendar. It is only fitting to say that the ever continuing saga of continued fractions is an ode to the mortal geniuses who created these immortal melodies.

References

• [1]Dani, S.G. Geometry in the Śulvasūtras, Studies in the History of Indian Mathematics (Ed. C.S. Seshadri), chom 5, Hindustan Book Agency, 2010.
• [2] Datta, B. Ancient Hindu Geometry: The Science of the Sulbas, Calcutta Univ. Press, 1932, reprinted Cosmo Pub., New Delhi, 1993.
• [3] Dutka, J. On the Gregorian revision of the Julian calendar, Math. Intelligencer, 10 (1988) no.1, 56–64..
• [4] Frederick, R.V. Mathematics of the Gregorian calendar, Math. Intelligencer, 7 (1985), no. 1, 53–56.
• [5] Gabai, D. and Kerckhoff, S.     William P. Thurston: 1946–2012, Notices of the AMS, 62, no. 11 (2015) 1318–1332.
• [6] Khinchine, A.I. Continued Fractions, Mineola, N.Y. : Dover Publications, 1997, (first published in Moscow, 1935)
• [7] Lenstra Jr., H.W. Solving the Pell Equation, Notices of the AMS, 49, no. 2 (2002) 182–192.
• [8]Silverman, J.H. A Friendly Introduction to Number Theory, Fourth Edition, 2012 Pearson Education, Inc.
• [9]Thomas, I. Greek Mathematical Works II, 1941
• [10]Vardi, I. Archimedes’ Cattle Problem, The American Mathematical Monthly, 105, no. 4 (1998) 305–319.

Footnotes

1. The spring equinox is the day in March (for the northern hemisphere) when the day and night are of approximately equal length, marking the beginning of spring. On this day, the sun’s path across the sky is midway between its lowest path in winter and its highest path in summer. ↩