Math and Motion:
A look at Chebyshev’s Works on Linkages

On the occasion of the 200th year of Pafnuty Lvovich Chebyshev’s birth, we survey his works on mechanical linkages. Let us first explain the main object considered in this paper. A mechanical linkage is a set of rigid bars connected with each other at the ends by revolving hinges. This construction can move and bend in the hinges and take different configurations. A natural example of a linkage is an arm of a human or a leg of an animal with its bones as bars and joints as links. The main purpose of linkages is to produce different kinds of motions, and humankind has been using them in engineering since antiquity.

Several important inventions in this field were made in Europe during the Middle Ages, the Renaissance and also in modern times. For example, the pantograph—a tool for copying and scaling writings and drawings—was invented in the beginning of the 17th century by Christoph Scheiner (an illustration from his book Pantografice is represented in Fig. 1). But the most remarkable progress in the study and creation of mechanical linkages was made in Europe in the 19th century, when all branches of mechanics and engineering started developing rapidly as part of the Industrial Revolution. The geometrical and analytical properties of these mechanisms also gave a new impetus for research in purely mathematical fields, and this process was continued later in the 20th century. In the rest of this paper we survey the work in this field made by Chebyshev, one of the most influential 19th century mathematicians, and examine the connections between these results and the work of other scientists. For the convenience of the reader, we shall avoid technical details. Most of the illustrations are taken from Chebyshev’s original papers.

Chebyshev was interested in mechanics from a young age, but his research in this field started only after a voyage to Europe which he undertook in June–October 1852. It was a scientific trip sponsored by the Saint Petersburg Academy of Sciences. During this journey, Chebyshev established connections with famous European mathematicians and, alongside with his theoretical research, observed factories and workshops, learning about the latest achievements in engineering and machinery. After his return, in the period 1852–1856, he gave lectures on applied mechanics at the Alexandrovsky Imperial Lyceum, in addition to his work at the University of Saint Petersburg.

In 1854, Chebyshev published his first paper on linkages, which was soon followed by several extensions. Let us present a list of some of his works on this topic. These papers were written either in Russian or in French. All these works can be found in the French version of Chebyshev’s Collected Works [3].

1. The theory of the mechanisms known under the name “parallelograms”, 1854 [3][I, pp. 539-568];
2. On the modification of Watt’s parallelogram, 1861 [3][I, pp. 433–438];
3. On a mechanism, 1868 [3][II, pp. 51–57];
4. On the parallelograms, 1869 [3][II, pp. 85–106];
5. On the simplest parallelograms that are symmetrical with respect to an axis, presented in a congress of Association fran\c caise pour l’avancement des sciences in 1878, published in 1885 [3][II, pp. 709–714];
6. The simplest systems of linked bars, 1878 [3][II, pp. 273–281];
7. On the parallelograms that are constructed from three elements and are symmetrical with respect to an axis, 1879 [3][II, pp. 285–297];
8. On the parallelograms that are constructed from three elements, 1879 [3][II, pp. 301–331];
9. On the simplest parallelograms that deliver the rectilinear motion up to the fourth order, 1881 [3][II, pp. 359–374];
10. A theorem related to Watt’s curve, 1881 [3][II, p. 715];
11. On the transformation of the circular motion into a motion alongside certain lines with the aid of linked systems, 1884 [3][II, pp. 726–732];
12. On the transformation of the circular motion into a motion alongside certain lines with the aid of linked systems, 1884 [3][II, pp. 726–732];
13. On the transformation of the circular motion into a motion alongside certain lines with the aid of linked systems, 1884 [3][II, pp. 726–732];
14. On the transformation of the circular motion into a motion alongside certain lines with the aid of linked systems, 1884 [3][II, pp. 726–732];
15. On the simplest linked system that delivers motions symmetrical with respect to an axis, 1889 [3][II, pp. 495–540].

These works can be considered as multiple parts of one long line of research. The word “parallelogram” that appears in several titles of these papers was first used to denote a specific mechanism, namely, Watt’s parallelogram, and its improvements. In later works, it was used by Chebyshev to denote linkages somehow related to this mechanism. The titles of the papers have a mechanical connotation, but the content of most of them is purely mathematical. It is worthwhile to say that Chebyshev used linkages to develop the theory of approximations of functions.

The bars of a linkage are related via algebraic relations between the coordinates of the links or chosen points on the bars. Therefore, if the position of some points of the linkage on the plane are fixed, then the trajectories of the other moving points are algebraic curves. The natural questions that arise here are: What kind of algebraic curves can be obtained by these motions? What curves on the plane can be approximated by the curves traced out by chosen points on the linkages? Although Chebyshev turned his attention to the general theory of approximations, these questions remained important. William Thurston and Nikolai Mnev turned the gaze back to these questions in the last quarter of the 20th century, resulting in proving a series of universality theorems for linkages. For an exposition of the modern history of this question see~[2].

Now we shall say a few words about Watt, since Chebyshev refers to him in several of his papers. James Watt (1736–1819) was a Scottish engineer, and one of the pioneers of the Industrial Revolution. One of his famous inventions was an improvement of the steam engine (the first steam engine invented by Thomas Newcomen was extremely inefficient). Watt’s name is also used to denote a SI unit of power.

Chebyshev, in his works, explicitly refers to “Watt’s parallelogram”. Formally, there are two linkages which are denoted by this name, the reduced one (“Watt’s linkage”) being a part of the full one (“Watt’s parallelogram”). We shall explain first the reduced one (Fig. 4).
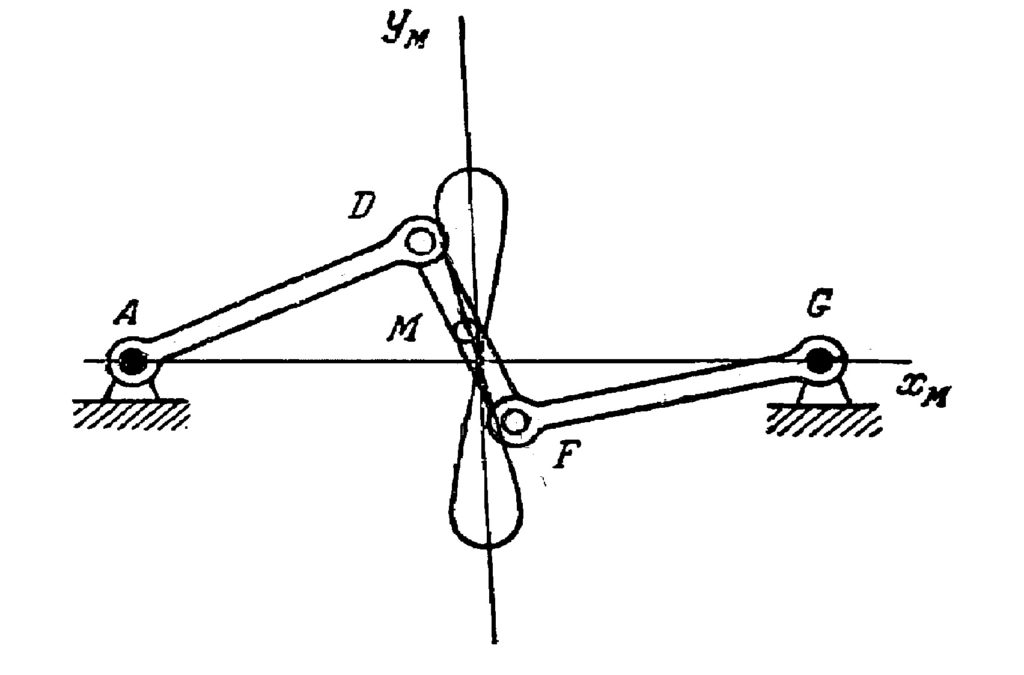
It consists of three bars linked in a chain with the positions of the two ends of this chain fixed. The two bars on the sides can rock around the fixed points at some degrees and the trajectories of the nodes D and F are segments of circles. Every point M on the middle bar has a specific trajectory, which is called Watt’s curve and can be defined with an equation of degree six. If the rockers are of the same length and the point M is in the middle of the bar DF, then a certain segment of the trajectory of the point M approximates a straight line, and this approximation is the goal of this whole construction. This linkage remains in use today, for example, in some car suspensions to prevent relative sideways motions between the axle and the body of the car (Fig. 5).

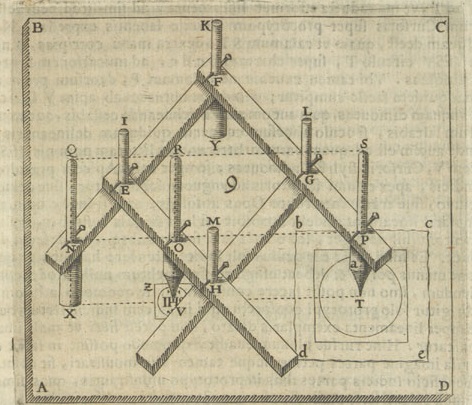
Watt’s parallelogram is obtained by combining Watt’s linkage with a pantograph (a parallelogram). It was used in steam engines to translate circular motion into rectilinear. The full mechanism is shown in Fig. 6, where Watt’s parallelogram is the upper part of it. The machine transforms the circular motion of the point K through the rocking of the points E and B into an almost rectilinear motion of the points M and C, which enables a truly rectilinear motion of the piston S, but with some side tension. Chebyshev wrote about this mechanism in his report on the journey of 1852 [3][II pp. VII–XIX]. He noted a lack of underlying theory for this invention, which led to certain problems for its improvement and alterations. Such alterations and improvements were needed for two reasons.

First, if the two rockers of Watt’s linkage were not equal in length, then the optimal choice of the point M was not known. Second, even with the perfect choice of this point, the low precision of the “rectilinear” motion achieved by this mechanism resulted in a quick deterioration of the machines, thanks to the side tension. Chebyshev wrote that the only works in analysis related to this problem were ones of C.-N. Peaucellier¹ (he does not mention the titles of these works). He also mentions in the same report that his reflections on these mechanisms led him to analytical problems “of which little is known at the moment”.

The first work in the preceding list is a 25-page paper where Chebyshev developed a theoretical foundation for solving problems such as finding the optimal proportions for Watt’s mechanism. He reformulated the question in purely mathematical terms, and stated a much more general problem:

This was the starting point of a new mathematical school of the approximation of functions, which led to results far beyond purely mechanical questions.

In the other papers of our list, Chebyshev presents mechanisms with various properties that provide approximations to rectilinear motion. The paper 2 proposes an improvement of Watt’s parallelogram (Fig. 7). This linkage transforms the rocking of the bar AB into an almost rectilinear vertical motion of the point C. Comparing his calculations with the calculations done by G.~de Prony² in [4], Chebyshev concluded that it was indeed an improvement and noted that the new mechanism achieved the accuracy needed by modern industry, while being not too complicated at the same time, so that no further improvements in this direction were needed. Nevertheless, in the paper 4, Chebyshev continued his research and developed a way to construct a mechanism that produces rectilinear motion up to any precision desired. Naturally, the complexity of the constructed mechanism was growing with increasing precision. Chebyshev also derived an equation that should hold for any linkage with one degree of freedom: 3m-2(n+v)=1, where m is the number of the bars, n is the number of free links and v is the number of the fixed points of the linkage.

In his other papers, Chebyshev studied simple mechanisms. In the paper 3, he discussed the mechanism presented in Fig. 8[a]. Like Watt’s linkage, it consists of three bars joined into a chain, with two endpoints fixed. But this time the two side rockers are much longer and are supposed to stay crossed. With this condition, the trajectory of the point M, moving from one side to another, is very close to a horizontal line. In the French literature, this mechanism is called “Chebyshev’s horse” (“Cheval de Chebyshev”). Chebyshev applied the theory that he had developed in his first paper to this mechanism, found the optimal proportions for it, and proved that in the optimal case it has better precision than Watt’s linkage. In his talk at a Congress of the Association française pour l’avancement des sciences in Paris in 1878, the content of which was published later as the paper 5, he mentioned that this mechanism had found a lot of applications in engineering.

In the paper 5, Chebyshev studies an alteration of this mechanism – by moving the point M away from the line AA_1 (which in fact turns this bar into a triangle, see Fig. 8[b]) and finding the optimal proportions for such a mechanism. It turns out that there are four different optimal cases, all of which give equally precise approximation of rectilinear motion with the trajectory of the point M (Fig. 9). Chebyshev continued his study of this linkage in the paper 7, giving instructions and simpler formulae for constructing such linkages with desired properties (precision and range of the movement of the point M). In the paper 8, Chebyshev broadens the class of considered linkages by including non-symmetrical ones, and finds the optimal proportions in this case. He showed that the precision delivered by the optimal non-symmetrical linkages of this type is not greater than the precision of the optimal symmetrical ones. The paper 9 continued this research by describing linkages of the same type, but that deliver less precise rectilinear motion (up to degree four, whereas the optimal linkages deliver precision up to degree five). The weakening of the demand on the precision gives more freedom in the construction of these linkages.

In the paper 6, Chebyshev developed other linkages that provide the same movement as a linkage of the form in Fig. 8[a] or Fig. 8[b]. He proved a theorem that states that the same motion can be produced by different four-bar mechanisms. This result is known now by the name “Roberts–Chebyshev Theorem”. Chebyshev also presented a simple mechanism shown in Fig. 10[a] that is now called “Chebyshev’s lambda-mechanism” (since its form resembles the Greek letter \lambda). It consists of three bars and has two fixed points. While the point B moves along its circular trajectory, the trajectory of the point M has two parts: a “straight” part, and a “curved” one. On the basis of this lambda-mechanism, Chebyshev constructed his walking machine that attracted a lot of interest at the third Paris World Fair in 1878. The other result of this paper is the so-called “Chebyshev straightener”, Fig. 10[b]. The whole trajectory of the point M of this linkage is close to a straight line.

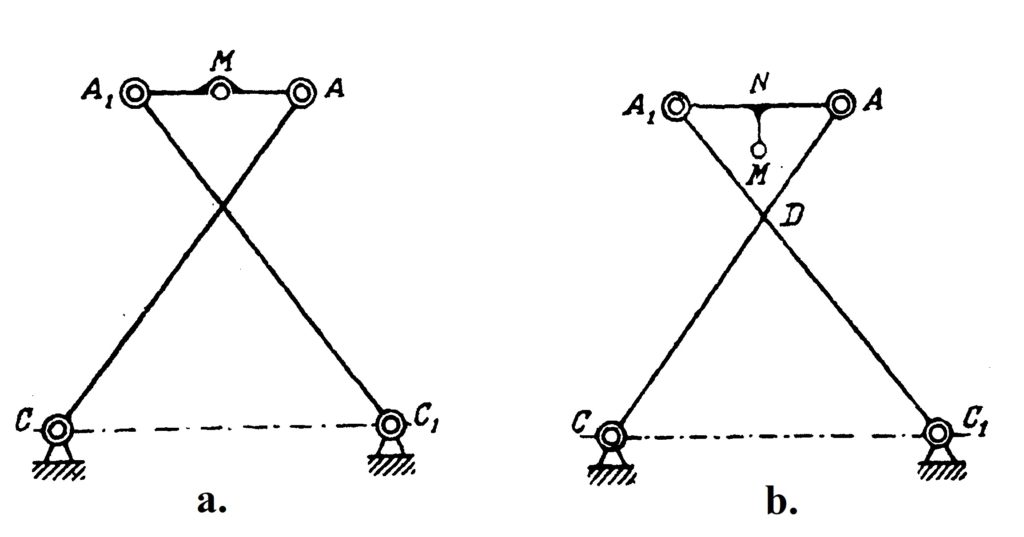
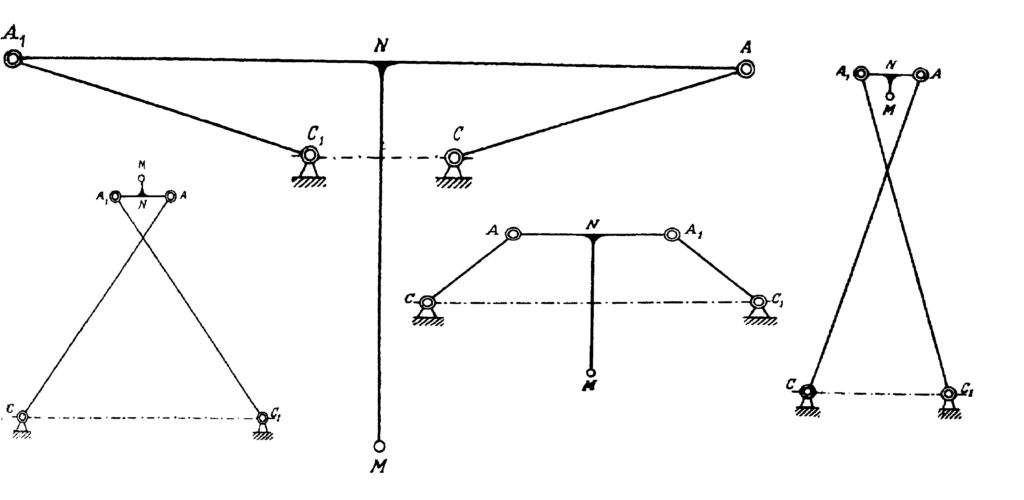
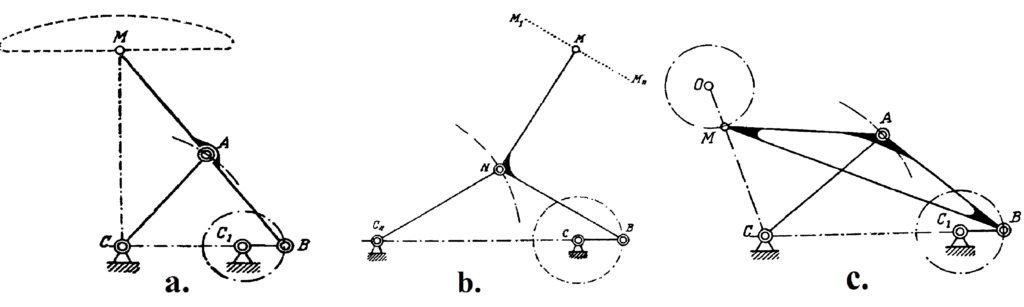
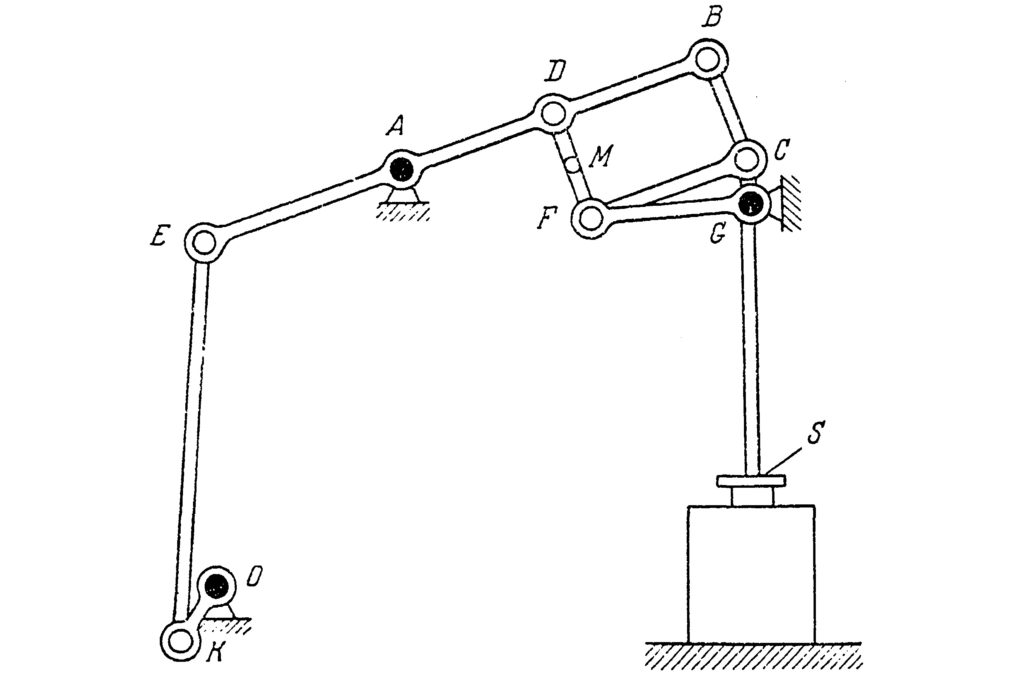
The one-page note (Paper 10) gives a theoretical boundary for the precision of the movement delivered by Watt’s mechanism. The paper 11 discusses three mechanisms shown in Fig. 10 that were invented by Chebyshev. We have already talked about the first two of them, which appeared in the paper 6, so now we shall comment on the last one. It is the four-bar reversing mechanism. The trajectory of the point M here is almost circular and the direction of its circular motion is opposite to the direction of the point B.

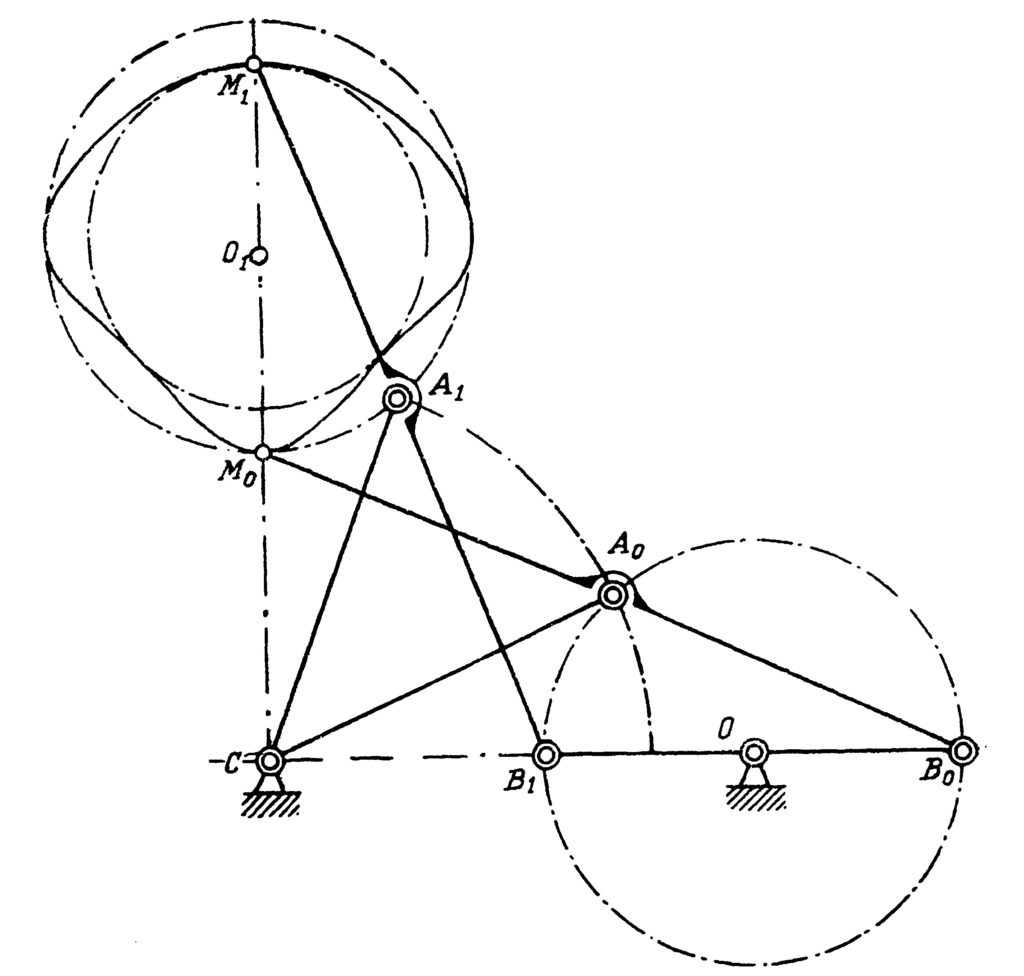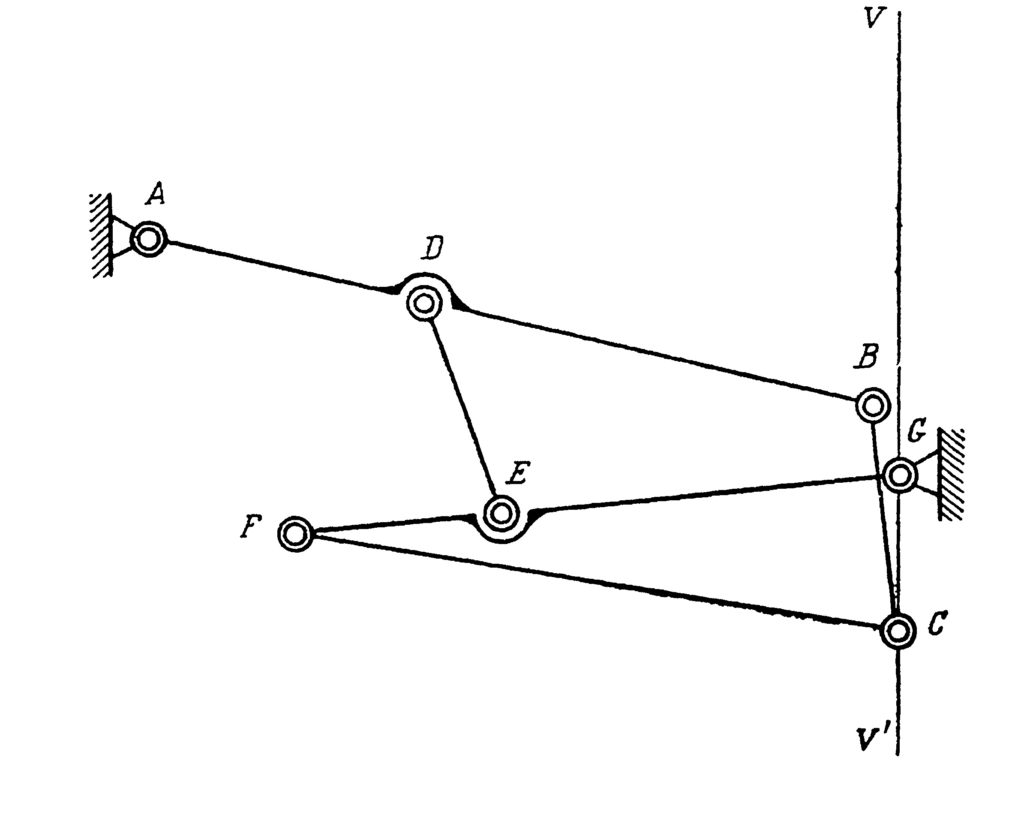
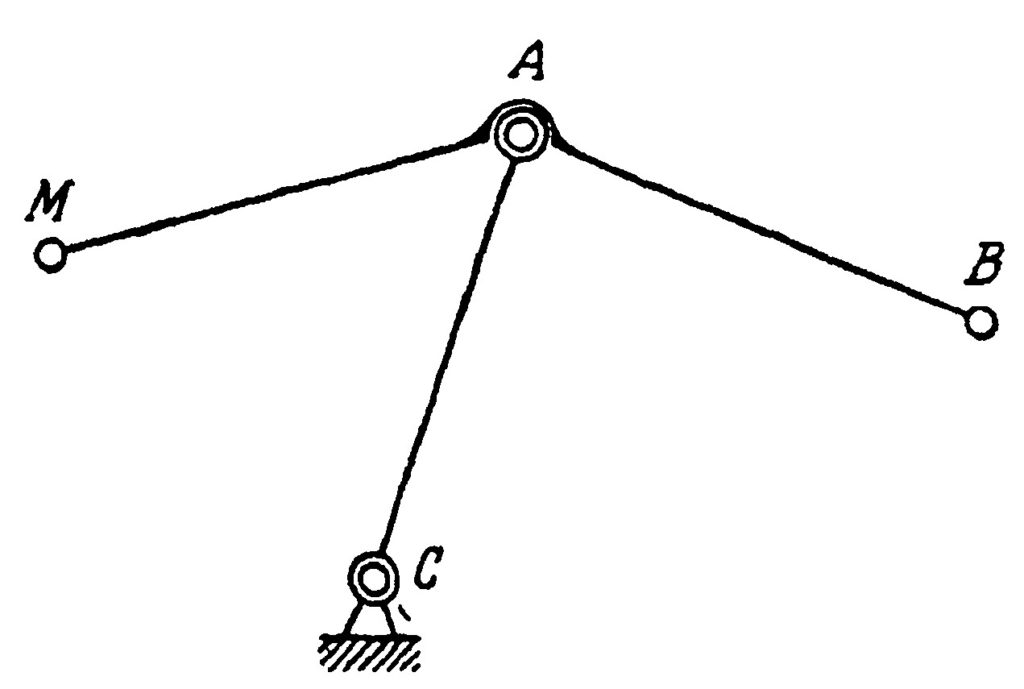
In the last paper of our list, Chebyshev studied the possibilities of the simple system represented in Fig. 11. The point B is a hinge, but the angle MAB is fixed. All three mechanisms in Fig. 10 contain such a system, but with different values of this angle. This system transforms a motion of the point B into a motion of the point M, and Chebyshev in this paper studied various possibilities of such a transformation. For example, if you change the radius of the circulation of the point B in the lambda-mechanism, which incidentally should be exactly \frac{|AB|}{5}, you will get a completely different trajectory of the point M, see Fig. 12. This example shows the importance of the exact proportions of the linkages. Although the linkage in Fig. 12 has a nice property—that the trajectory of the point M lies strictly between two concentric circles—it circulates in a direction opposite to the direction of the circulation of the point A. This linkage is the basis for another of Chebyshev’s inventions, the “six-bar reversing mechanism”.

We have surveyed the almost 40-year work of Chebyshev in inventing and analysing mechanical linkages. This is only a part of his work; it does not reflect the whole gamut of his scientific interests, which was very broad. This research can serve as an illustration of how theory and practice support and develop each other. This synergy was one of the driving principles of Chebyshev’s work; it showed how unsolved practical questions can give rise to new perspectives in completely different fields of mathematics.

On the basis of the linkages described in these papers, several other inventions were made by Chebyshev. Models of mechanisms invented by him can be found in science museums in Russia, France and Great Britain. The animated versions of these machines can be found online on the site [5], created by Mathematical Etudes Foundation.\blacksquare

References

1. A. Papadopoulos, Pafnuty Chebyshev (1821-1894), in this issue of Bhāvanā.
2. A. B. Sossinsky, Configuration spaces of planar linkages, Handbook of Teichmüller Theory (VI), editor: A. Papadopoulos, IRMA Lectures in Mathematics and Theoretical Physics, European Mathematical Society, 2016, 335–374.
3. P. L. Chebyshev, Works (French), edited by A. Markov and N. Sonin, Imprimerie de l’Académie Impériale des sciences, Saint Petersburg, 2 volumes, 1899–1907.
4. G. de Prony, Sur le parallélogramme du balancier de la machine à feu, Annales de Chimie et de Physique, XIX; Annales des Mines, série 1, XII.
5. Mechanisms by Tchebyshev, https://en.tcheb.ru/

Footnotes

1. Charles-Nicolas Peaucellier (1832–1919), a French engineer. ↩
2. Gaspard Clair François Marie Riche de Prony (1755–1839), a French mathematician and engineer, who worked mostly on hydraulics. ↩

Letter from the director of the Conservatoire National des Arts et Métiers (National Conservatory of Arts and Crafts) to Chebyshev about the second model of the arithmometer and the donation of the model of slider-crank mechanism of the steam engine Nikolai Andreev, tcheb.ru