
In the inaugural issue of Bhāvanā, the article ”The coming of age of Mathematics in India” by Raghavan Narasimhan mentions several centres of mathematical activity in India and Indian mathematicians about whom “people outside India, and even most Indians, know very little’’. Hansraj Gupta was among the mathematicians to figure in that article, as a “number theorist from the Punjab’’. The three articles presented here offer a quintessential picture of Hansraj Gupta. While the biographical sketch by Som Dutt Chopra, published in 1991 in the Journal of the Indian Mathematical Society, serves to give some insights into his life, the second one – Men in my life – that appeared in the Collected Works Series of the Ramanujan Mathematical Society is an autobiographical account of Hansraj Gupta himself; in this, he talks about people whose goodwill and support encouraged him to embark on a career in mathematics. The text of his presidential address in 1963 to the Indian Mathematical Society that appeared in their ninety year old publication The Mathematics Student is the third article. Bhāvanā records its deep appreciation to the three original sources for their kind permission to reproduce them here, as a warm tribute to the memory of Hansraj Gupta, to portray his life of dedication and service to mathematics and mathematical community.
We begin with a couple of representative titbits from his work that may serve as a quick introduction.
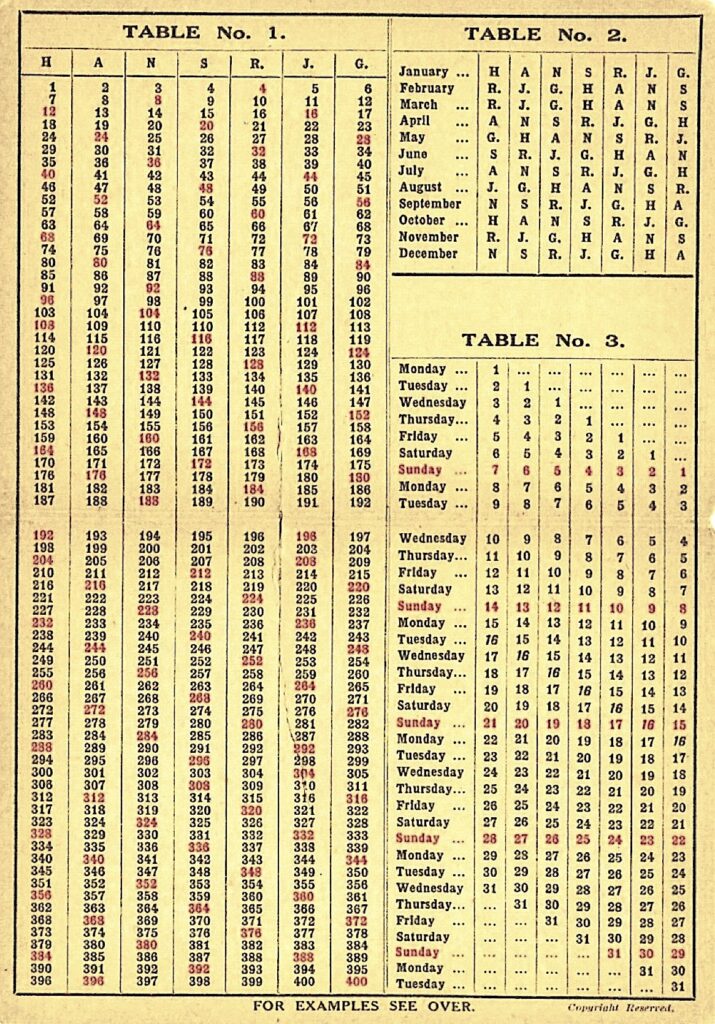
The calculation of the day of the week for a given date as per the Gregorian calendar fascinates many young students. The periodicity (or lack of it) of leap years every 4 years, 100 years and 400 years in the Gregorian calendar adds to the challenge. Hansraj Gupta too seems to have been captivated by this problem early on in his life. So much so that he devised a compact, easy-to-use look-up table to find the day of the week for any given day. This “perpetual calendar” [4] was his first publication as well. In present times of course, a simple internet search will instantaneously tell us the day of the week for any given date, but interestingly, even modern technology can have its own limitations. For example, the “WEEKDAY function’’ in Microsoft Excel2 returns the day of the week for a given date, but does not work for dates prior to 1 January 1900. Whereas Gupta’s perpetual calendar, devised hundred years ago, does not have such limitations!
The number 7 assumes significance in the calculation of the day of the week because the days of the week repeat with a periodicity of seven days. Gupta playfully chooses seven letters he needed for the perpetual calendar such that they spell out his own first name (well, almost) at the top of Table 1 (see Figure 1). It is our guess that since the letter A appears twice in HANSRAJ, he has skipped the second A, and instead used the first letter of his surname to end up with HANSRJG.
The topic of calendars seems to have continued to intrigue him and he wrote several other pieces on the subject even in his later years. The perpetual calendar was the first of 190 papers and 6 books and monographs published by Hansraj Gupta on a variety of topics.
 |
 |
Apart from his fascination with calendars, the partition function was another subject that piqued his interest. How he got interested in partitions is itself an interesting anecdote that he recalls in his recollection “Men in my Life” included in this issue. Therein we read about one of his earliest contributions about partitions which set off a chain of events involving several mathematicians, starting with disproving a conjecture made by Srinivasa Ramanujan (see [6]), leading to modifications of this conjecture and ending with proofs of the modified conjecture.
The partition function p(n) is defined as the number of ways that the positive integer n can be written as a sum of positive integers. For example, the first few values are: p(1)\;=\;1; p(2)\;=\;2 (1+1,2); p(3)\;=\;3 (1+1+1,2+1,3); p(4)\;=\;5 (1+1+1+1, 2+1+1, 2+2, 3+1, 4). By convention, p(0)=1. Major MacMahon had published tables of p(n) up to n=200 and Ramanujan had confirmed that his conjecture held for all these cases. However, in terms of formally proving this conjecture, Ramanujan had only been partially successful. His conjecture was as follows:
If x=5^{a}7^{b}11^{c} and 24y\equiv 1 (\!\!\!\!\mod x) [i.e., dividing 24y by x leaves the remainder 1], then the values
p(y),\,p(y+x),\,p(y+2x),… \equiv 0 (\!\!\!\!\!\!\mod x)[i.e., p(y),\,p(y+x),\,p(y+2x), etc., are perfectly divisible by x]. Among other things, he had not been able to prove his result for when the power of seven is greater than 2, i.e., when b\geq3. As neither a general proof, nor tables for n>200, were available, this is where the matter rested till Gupta calculated and extended the tables of p(n) up to n=300.
Now, for x=5^{0}7^{3}11^{0}=7^{3}=343, as per Ramanujan’s conjecture, one should have p(243)\equiv 0 (\!\!\!\!\mod 7^3) (in other words, dividing 24\times 243 by 343 leaves the remainder 1). The value of p(243) being available now, thanks to Gupta’s extended table, it was Sarvadaman Chowla who noticed (see [2]) that here was a case where Ramanujan’s conjecture was failing. As per the table, p(243)=133978259344888, which was not divisible by 7^3. Chowla got one of his students to calculate all p(n) up to n=243 and confirmed that the value of p(243) found by Gupta was indeed correct. Subsequently, Ramanujan’s conjecture was modified and proved by G.N. Watson for higher powers of 7 (see [7]). The conjecture for all powers 11 was later proved by A.O.L. Atkin (see [1]).
While Gupta’s role in the above sequence of events could possibly be construed as merely incidental, he actually wrote about 70 papers on partitions through which he directly contributed new results, solutions of many conjectures, and simplifications of several proofs. Other than calendars and partition functions, he also made contributions in the fields of representations of primes by quadratic forms, symmetric functions, Diophantine equations and combinatorics as has been highlighted in the articles dwelling on his work in the two volumes of his collected papers.
We conclude this introductory preamble by quoting from a graphic reminiscence of his impactful style of teaching, recalled in the article [3] by V.C. Dumir and R.J. Hans-Gill;
References
- [1] A.O.L. Atkin, Proof of a conjecture of Ramanujan, Glasgow Math. J. 8 (1967), 14–32.
- [2] S. Chowla, Congruence properties of partitions, J. London Math. Soc., 9 (1934), 247.
- [3] V.C. Dumir, R.J. Hans-Gill, Mathematical Contributions of Professor Hansraj Gupta, J. Indian Math. Soc. 57 (1991), 11–16.
- [4] Hansraj Gupta, Gupta’s Perpetual Calendar for finding the Day of the Week, J. Indian Math. Soc. 15 (1923), 65–68.
- [5] Raghavan Narasimhan, The coming of age of Mathematics in India, Bhāvanā, Vol. 1, Issue 1, January 2017, 36–50.
- [6] S. Ramanujan, Some properties of p(n), the number of partitions of n, Proc. Cambridge Philos. Soc. 19 (1919), 207–210.
- [7] G.N. Watson, Ramanujans Vermutung über Zerfallungsanzahlen, J. Reine Angew. Math. 179 (1938), 97–128.
Hansraj Gupta (1902–1988): A Biographical Sketch By S.D. Chopra3
Hansraj Gupta,4 son of Shri Jati Ram Gupta and Smt. Bhagirithi, was born on 9 October 1902 in the house of his maternal uncles at Rawalpindi, now in Pakistan. He was the eldest of four brothers and three sisters. The family belonged to Samana, a small town in Ambala district. Shri Jati Ram was a Tehsildar in the erstwhile Patiala state. Hansraj Gupta spent most of his childhood at Rawalpindi with his uncles who were doing well there as government contractors in the cantonment area. He received all his school education there and passed the Matriculation examination of the Punjab University, Lahore in 1919 from Denny's High school, Rawalpindi, in high first division winning a University scholarship.
Hansraj Gupta then joined the Mohindra College, Patiala for his under-graduate education and passed the Intermediate examination in 1921 in high first division winning a Patiala State scholarship. He passed the BA examination from the same college in 1923 in high second division. Hansraj Gupta had shown his devotion to mathematics from his school days when he devised his 100 years calendar. While an undergraduate student, he devised his perpetual calendar which was exhibited at the British Empire Exhibition at Wembley, a suburb of London, in 1923 and was awarded a medal and a certificate of merit. He had to go to Lahore for his MA in Mathematics since teaching was available only at Lahore. It is believed that he was not too well during most of 1923–24 and so could not join a college at Lahore immediately. Fortunately for him, the Mohindra College was affiliated to the Punjab University for MA in Mathematics but had no arrangements for teaching. Hansraj Gupta enrolled there for the MA Mathematics course without the necessity of having to attend any lectures, thus saving a year. In 1924, he migrated to the Dayal Singh College, Lahore for the second year of the MA course. Possibly, he chose that college because its Principal, Pandit Hemraj, enjoyed a very high reputation both as a mathematician and a teacher. Hemraj also had some papers in number theory to his credit. Hansraj Gupta passed the MA examination in Mathematics in 1925 in high second division, standing first in the university, a very creditable performance since he had only one year of formal study for the course. Obtaining a first division in the MA was a rather rare thing in those days as the Punjab University was said to have produced only about half a dozen first divisions in the first forty years of its existence, having been established in 1885.
Hansraj Gupta was the first PhD in mathematics to be awarded by the Punjab University, Lahore


Hansraj Gupta would have liked Professor S. Chowla, the eminent number theorist, to return to India
I first heard of Hansraj Gupta in 1936 when I was a student of BA at the Dayal Singh College, Lahore. That was when Hansraj was awarded the PhD degree in Mathematics by the Punjab University, Lahore, the first PhD in mathematics to be awarded by that university in over fifty years of its history. The thesis entitled Contributions to Theory of Numbers was examined by two of the most eminent number theorists of the time, Professors G.H. Hardy and J.E. Littlewood of the University of Cambridge, England, who found the thesis to be well above the standard of the average PhD thesis. As Hansraj Gupta was an alumnus of the Dayal Singh College, the news was duly publicized in the college, and the college and its students had cause to be proud of his achievement. His handwriting was very good, comparable to that of a typewriter. Further, in those days, typing facilities, particularly for typing tables, were not good. So as a special case, Hansraj Gupta was permitted to submit handwritten copies of his thesis.
He was permitted to submit handwritten copies of his thesis, as a special case
I met Hansraj Gupta first in the summer of 1940 with a letter of introduction from his father-in-law, Professor Mulraj of our college. I had gone to Hoshiarpur for an interview for the post of Lecturer in mathematics at the local DAV [Dayanand Anglo Vedic] College, which had just been raised to the degree standard. I was duly impressed by Hansraj Gupta's sincerity and kindness. He was even frank to tell me not to mention at the interview that I had met him. There was some kind of rivalry between the two colleges over admissions, the DAV College being more keen to do better than the Government College in the numbers admitted. I got the post and joined the college in September 1940 and for the next two years we were meeting quite often. I left the DAV College in November 1942 to join our alma mater at Lahore. A second contact with Hansraj Gupta came when I was posted to the Mathematics Department of the Panjab University in 1957 on my return from Cambridge after obtaining a doctorate. Thus began another three years of closer contact until I left the Panjab University in 1960. In those days the department was only a fraction of its present size and all of us were like the members of a family with Hansraj Gupta as the father figure.

Hansraj Gupta joined the Indian Mathematical Society in 1923, while he was still an undergraduate, and perhaps had the record of longest membership of the society. He was elected president of the society in 1963 and presided over the Annual Conference of the society held that year at Madras. He was elected a member of the Edinburgh Mathematical Society in 1936 and of the American Mathematical Society in 1960. While still a lecturer, he was elected in 1950 to the prestigious Fellowship of the National Institute of Science of India, now known as the Indian National Science Academy. He was also a Fellow of the National Academy of Sciences, India, and a member of the Indian Science Congress Association and was the President of the Section of Mathematics at the combined 51st and 52nd Annual Session of the Science Congress held at Calcutta in 1964. The Mathematical Association of India honoured him with its Distinguished Service Award in 1979.
In 1954, the first chance to go abroad came Hansraj Gupta's way, when Professor M.V. Wilkes, Director, Mathematical Laboratory of the University of Cambridge, England invited him to go to Cambridge and work at the Laboratory. This was in recognition of his talent. However, he could not avail of this invitation for domestic reasons. Hansraj Gupta was Visiting Professor at the University of Colorado, Boulder, USA in 1962–63, Arizona University, Tucson in 1966–67, and University of Alberta, Edmonton, Canada in 1969–70. He also represented the Indian National Science Academy at the International Congress of Mathematicians, Vancouver, BC., Canada, in 1974.

References to Hansraj Gupta’s work have been made in several standard texts and some of his work included in some of these. To mention a few: (i) Encyclopaedia Britannica, Vol. 16, p. 604 under the article on “Theory of Numbers’’; (ii) Theory of Numbers by G.H. Hardy and E.M. Wright; (iii) Guide to Mathematical Tables by D.H. Lehmer; (iv) Additive Zahlen-theorie by Hans-Heinrich Gatmann; (v) Ramanujan by G.H. Hardy; (vi) An Introduction to Combinatorial Analysis by John Riordan; (vii) Mehrgradige Gleichungen by Albert Golden, and (viii) Hand-Book of Mathematical Tables, National Bureau of Standards, USA. The National Bureau of Standards also invited Hansraj Gupta to write a survey article on Theory of Partitions for publication in their Journal. The article appeared in 1970 and is considered one of the best surveys on the subject.
Until 1947, and for some years after, India was completely dependent on the British for all its arms and the relevant ballistics tables. With D.S. Kothari as the Scientific Adviser to the Ministry of Defence the need was felt for India to have its own ballistics tables. So an Advisory Board for Ballistics was constituted in 1953 and Hansraj Gupta was appointed one of its members. Later, he was also entrusted with a project to calculate new ballistics tables. Professor Cheema, then a research student with Hansraj Gupta was working on these tables when I joined the department in 1957.
Hansraj Gupta was not only a dedicated researcher but also a dedicated teacher. He enjoyed a very good reputation as a teacher and took interest not only in the academic progress of his students but also in their all round welfare. To use a Cambridge phrase, he was in true sense in loco parent to his students, who in turn called him “Papa ji’’ just like his own children. Besides being a teacher and a researcher, Hansraj Gupta was ever eager to learn. Professor A.M. Vaidya of Gujarat University, who joined Hansraj Gupta as research scholar in September 1961, writes: “I suppose one of his greatest regrets was that although his main work was in partition theory, he had not been able to follow the seminal work of Hardy and Ramanujan on partitions. At the age of 60, he had the opportunity to study that work and he had no hesitation in putting long hours of work and effort. We were in the University of Colorado in the USA in 1962–63. He and I met every day for about a month at his residence and spent several hours studying Rademacher’s TIFR lectures on Hardy-Ramanujan theory. It was tough going and he insisted that once we follow an argument, I should write it down in my own way. This way, I had my own notes on Hardy-Ramanjuan theory at the end, and both of us had finally understood (if not mastered) the famous circle method of Hardy-Ramanujan.’’
Hansraj Gupta was not only a dedicated researcher but also a dedicated teacher
After shifting to Allahabad, Hansraj Gupta was associated with the Department of Mathematics of Allahabad University under the scheme of the University Grants Commission for Outstanding Retired Teachers. However, he was not very happy with the situation there as he once expressed to me, and later to Professor Vaidya. During his long stay there not one person approached him for guidance in research in number theory. Perhaps, with the advent of the electronic digital computers, the days of Hansraj Gupta's kind of computational work were over. My last correspondence with Hansraj Gupta, a few years before his death, was about the possible publication by the Kurukshetra University of a table of some functions which he had prepared with the assistance of S.P. Khare. He had been sanctioned a grant of the equivalent of 1000 dollars by the University Grants Commission in the early eighties for the possible publication of these tables in some journal. The Panjab University through whom the grant was sanctioned no longer seemed to be interested in their publication and the grant had already lapsed. I made the necessary enquiries and found that the grant needed to be revived and enhanced at least four times for publication in book form. Hansraj Gupta no longer had the energy to get all this done and so the tables could not be published.
Hansraj Gupta was rather unfortunate in his matrimonial alliances. None of his three marriages lasted long. He had one daughter by his first wife and the second died issueless. His third wife, daughter of our teacher Mulraj of Dayal Singh College, Lahore, gave birth to three daughters and a son, and passed away thereafter. Three time widower, he decided not to marry again. When I met him in 1940, an old widowed aunt was living with him and looking after his household. All five children are happily settled. The elder two daughters are married to businessmen, the husband of the third is a professor of mathematics in the [United] States, and the youngest is married to a very senior officer in the Income Tax department. This last was an intercaste marriage and, Hansraj Gupta having orthodox views on the subject, took some time to reconcile himself to this marriage. The son, an engineering graduate, after doing service with a big industrial company, is now running his own business. Throughout his thirty years of stay at Hoshiarpur, Hansraj Gupta continued to live in the mandi area which was built in the form of a quadrangle with a large open space surrounded by rows of houses on all four sides. It seems to have been built originally as a grain market. It was convenient also as both the Government College and the railway station were within a few minutes walking distance. Some of Hansraj Gupta's colleagues also lived in the same area and Hansraj Gupta had the best of relations with them. Hansraj Gupta believed in plain living and high thinking. He was deeply religious and the family said their evening prayers together regularly. The family lived a modest decent sort of life.
Hansraj Gupta was generous in helping others. In spite of the fact that he could not be said to be too well off, he was always supporting somebody or the other besides his own children. An instance of his desire to serve others was his interest in homoeopathy. He was a good amateur homoeopath, providing not only free consultation but also free medicines to those who came to him. Even when travelling he usually carried his small cubical box containing the essential medicines of common use. He once cured a case of chronic illness in my own family with a single dose. When I asked him how he got interested in homoeopathy, he related this incident. The nameplate outside his residence was inscribed “Dr. H. Gupta’’. One evening a villager came to his residence accompanied by a boy who had suffered some minor injuries, and wanted Hansraj Gupta to give the boy the necessary medical aid. Hansraj Gupta tried to convince the villager that he was not a medical doctor but the villager refused to believe him, not having heard of any other kind of a doctor. Ultimately Hansraj Gupta attended to the injuries as best as he could and got rid of them. After this incident he decided to become something of a medical man to be able to serve people. Since all other systems required some amount of formal training he chose to study the homoeopathic system in which the treatment is mostly symptomatic and less likely to have any adverse effects unless very high potencies are used. He served as commandant of a refugee camp after the partition of the country in 1947. In keeping with his religious nature he was also the president of the Gandhi Study Circle and the Gandhi prayer class at Government College, Hoshiarpur. Hansraj Gupta had a good sense of humour and could enjoy a joke even about himself. He was good company for the young and not so young both.

Acknowledgements: I have been helped greatly in writing the biographical sketch of the Late Hansraj Gupta by the various write-ups of his life and work which have been made available to me by the Editor, I.B.S. Passi. I am obliged to Shri M.R. Gupta, Retd. Assistant Registrar, High Court of Haryana and Punjab, a younger brother of Hansraj Gupta, for many details about the childhood and early life of Hansraj Gupta. I am greatly obliged to Shri Surya Kanta Gupta, son of Hansraj Gupta, for sending me a write-up of many important details of Hansraj Gupta’s life, and even more so for a Curricular Vitae of Hansraj Gupta up to the year 1966 which appears to have been prepared by Hansraj Gupta himself immediately after his retirement. Last, but not the least, I am thankful to A.M. Vaidya of Gujarat University for writing to me about his meetings with Hansraj Gupta and the impressions left on him.
Men in My Life6 by Hansraj Gupta
My education started when I was about six and was put in the charge of an old saintly muslim Maulvi Qalandar Baksh by name who had taught my father before me. He was known for his patience with children and his love for them. He had six or seven students at the time. The school was run in a single room tenement which was really meant to be a shop. It was hardly a furlong from our house in Samana – an old city in Patiala State. We were required to pay just one pice7 per week as fee and one pice for the accessories such as the earthen ink-pot, the black ink, the reed-pen and the knife which was needed for mending the pen a number of times each day. Every student brought cooked food for the Maulvi once a week from his home. The Maulvi took only one meal a day and was most of the time praying to God that is when he was not teaching. He taught us to read and write Urdu and numbers up to ten.
After some time, my father got me admitted to a regular school in the district head-quarters at Bhawanigarh. The school was about two miles from Phaguwala – the village where my father was a Patwari that is a petty revenue officer whose main function was to collect land revenue from the farmers and keep land records for the princely state of Patiala which was then ruled over by a Maharaja. My father had very good hand-writing and was good at arithmetic because he had to keep accounts of the revenue he collected. His officers invariably praised him for both. I naturally imbibed the two qualities from him.
On my father's side, we were not at all affluent but we had enough to eat and to spare. In fact my father was known for his hospitality in the area around and there was hardly a day when we did not have some guests. I remember we always had a cow or a buffalo in the house and milk was plenty.

The medium of teaching was mainly Urdu. One started learning Hindi and English from the fourth class. By the time the student reached the eighth class the medium of instruction had almost completely changed to English. My hand-writing and arithmetic soon started paying me good dividends. After I had been studying in the third form for a few months I was promoted to the fourth. I was hard-working and obedient and the teachers at that time wanted nothing more. At Denny’s High School, with the encouragement I received from my teachers, particularly from Ram Lubhaya Mall Sawhney, I fared very well. I was selected to sit for the Scholarship examination which the Inspector of Schools used to conduct for the middle standard students of the district. I stood second and won one of the scholarships. When I sat for the matriculation examination of the Panjab University in 1919, I was awarded a university scholarship.
I naturally imbibed the two qualities, good handwriting and being good at arithmetic, from my father
It was in Rawalpindi at the house of my maternal grand-father that I was born on the 9th October, 1902 and it was here that I received most of my school education. The year 1919 is well known in the history of India for the massacre of the people at the Jallianwala Bagh in Amritsar. It was just a few days before this unfortunate event that I left Rawalpindi for my father's place. At this time he was posted at village Channon about fourteen miles from Patiala – the seat of the state government. Here, there was the Mohindra College named after one of the earlier maharajas. All the expenses of the college were met by the state and no tuition-fee was charged from the students. The college was probably the oldest in the Panjab having been set up in 1875, but even so there were no science classes there then. My father decided to get me admitted to this college. He had a friend in Patiala – Pandit Kishan Chand. He was an advocate in the high court and was very well off. He had no son or any other child and when he learned that I had got admitted to the Mohindra College and I had even won a university scholarship, he himself offered to let me stay with him. Due to his short stature the Pandit was popularly known as “Babu Tiny”. In fact, I do not think many people knew his real name. His wife – Revti Devi, was a very kind-hearted woman. I stayed with them for five years and got the love of a mother and that of a father from them, which I had missed all my life. I used to go to sleep very early and it was this “mother” who used to come down from her room to wake me up at 4 a.m. They helped me as nobody else could have done.

Since there were no fees to be paid at the college and I was putting up with Babu Tiny, the scholarship money which I received during these four years was enough for my needs. In the BA examination, the university awarded a scholarship only to those students who had stood first in one or the other of the subjects. I did not top the list in any of the three subjects and did not win a scholarship. It was now that my problems began.
The MA teaching in mathematics was then being done only at Lahore – the seat of the Panjab University. My father could not afford to send me there where I would have to stay in the college hostel and pay for my tuition. Luckily the Mohindra College was affiliated to the university for MA in mathematics though no student had ever joined there for the purpose. I decided to take advantage of the situation and got the permission of the university to pursue my studies for MA at the Mohindra College. With a good word from each one of my teachers, the Principal agreed to admit me. My father was insisting that I take up some service. I made no serious effort to get a job but started coaching a few students privately and laying aside the money which I got from them. In this I had the full mental and moral support of Pandit Kishan Chand who knew more than my father what was really good for me.
Principal Hemraj taught us number theory and was responsible for exciting my interest in the subject
For one long year, I could get no job, except for the few months that I was tutor to the son of the Prime Minister of Patiala. Finally it was in August 1926 that I got an offer of a lectureship at the Sadiq Egerton College, Bahawalpur. Bahawalpur was then a muslim state ruled over by a Nawab. It is now a part of Pakistan. This area was very backward educationally and otherwise, but the people were very sincere and helpful. To them a lecturer at the State College was something very big and my students held me in great respect. The Principal, however, was not very well disposed towards me as I did not dance attendance on him while others did. He also did not like my being a vegetarian and of rather puritan habits. I stayed at this college for about two years before I got an offer from the principal, Government Intermediate College, Hoshiarpur. This I readily accepted. Hoshiarpur was then (as now) a district town in the Panjab, but educationally it was far behind Lahore the capital of the province. The college had started as a middle school some decades before.



There is one thing I must state here. Since I spent most of my time working at a small college in the mofussil where there was no library worth the name, there are hardly any references to other peoples' work in my papers. There are many results which I only rediscovered. My knowledge of the literature on the subject is very meagre. Only recently at Morgantown, West Virginia, Professor [Henry] Gould pointed out that the method of recording partitions of numbers which I had presented in my talk, had been known since 1796. I was not surprised at the information. What surprised me when I saw the Hindenburg paper (a copy of which he sent to me later) was that my presentation completely agreed with Hindenburg's – line for line.

There is a story about how my interest in partitions started. Sometime in 1929 or 1930, a student came to me with the following problem from his algebra book:
In how many ways can four mangoes be distributed among four persons when there is no restriction as to the number of mangoes any of them may receive?
The student had already been to a colleague of mine to whose class he belonged. Considering the mangoes to be of distinct types, he had obtained 4^4=256 as the answer to the problem. The student had come to me only because this answer did not agree with the one given at the end of the book. Luckily, I took the four mangoes to be alike and gave the following solution to the student:
There are several possibilities regarding the manner in which the mangoes can be distributed.
| Possibilities | Number of ways |
| Giving | |
| (i) all the mangoes to one of the persons | 4 |
| (ii) three mangoes to one and one to another | 12 |
| (iii) two mangoes to each of two persons | 6 |
| (iv) two to one and one each to two others | 12 |
| (v) one mango to each of the four persons | 1 |
| — | |
| Required number of ways | 35 |
| — |
My answer agreed with the answer in the book and the boy was very happy that I had been able to solve the problem for him.
Here the student's problem had ended but mine had begun. I had noticed that what really I had done was to partition 4 into at most four parts. I asked myself “How many partitions will a given number n have into a given number of parts?” This is what I started investigating, not knowing that the problem was not at all new and Ramanujan had calculated a table giving the number of unrestricted partitions of n\le 200. I had heard of Ramanujan for the first time in 1920 when my professor of philosophy at the Mohindra College had announced his death in his class. I had not seen Ramanujan's collected papers nor did I know anything about the pentagonal number identity of Euler. Could there be a more ignorant person than I?
Now I know a very simple solution to the problem the student had posed to me. I am glad I did not know it then, otherwise I might never have got interested in partitions. Ignorance is bliss sometimes! It was just a lucky chance that my table of partitions gave values of p(n) – the number of unrestricted partitions of n, for n\le 300. It enabled Professor S. Chowla to notice that Ramanujan's famous conjecture failed for the modulus 7^3, since p(243) was divisible only by 7^2 and not by 7^3. Actually finding that my table agreed with Ramanujan's for n\le 200, Chowla got the table recalculated by one of his students for values of n up to 243. I was happy that my value of p(243) was correct. Professor G.N. Watson proved the conjecture for all powers of 5 and revised it for powers of 7. Finally, A.O.L. Atkin proved the conjecture for all powers of 11.
In 1954, Panjab University appointed me professor of mathematics and chairman of the department, putting an end to my financial problems. But by then it was too late for me to start studying the literature on the subject. My appointment provided me with opportunities to visit the USA and Canada. I retired in 1966 but still continue to work in fulfilment of my promise to my teacher. I am now associated with the Panjab University as an honorary professor.
Presidential Address (General), by Professor Hansraj Gupta9
When I was still an undergraduate student, I used to look regularly into the pages of the journal of our society on the back cover of which appeared names of the members of the Executive Committee. Among those was the name of late Pandit Hemraj who was later my teacher in my MA classes. These names inspired me and I applied for membership of the society and was elected as such no less than forty years ago. During this long period, friends in the society were throwing suggestions regarding my election to the presidentship. I was successfully able to stand these onslaughts. Last year when I was away to the United States, my friends found their chance and got me elected to this high office. The fact was kept a guarded secret till a few days after my return from the States, Professor Bambah remarked that I would have to deliver three addresses and should get busy preparing them. I was of course aware of my election as President of the Mathematics Section of the Indian Science Congress but not of my election as President of the society and when he told me about it, I was not a little surprised. Being still in doubt a little, I hastened to confirm the fact from Professor V.S. Krishnan. Since the whole thing was done in secret, I have to thank my co-members in the society in a way different from the usual, and do so. I must warn them that if I fail it will be their responsibility.
For a considerable long time, eminent educationists all over the country have been feeling greatly agitated over the system of examinations prevalent in our universities. They have been raising their voice against it but no practical steps have so far been taken to change it. It is a matter which vitally concerns the students, the teachers and the universities. I would, therefore, take this opportunity, when so many eminent persons in the field of education and prominent citizens of Madras have assembled together, to make certain observations regarding this system.
In our present system of examinations the teacher has almost no hand in the assessment of his students. Examiners are appointed from the universities or institutions outside the state. They set the papers. In most of the universities there is no system of moderation even. Consequently the question papers very often contain questions which are beyond the course or the capacity of the students. Quite frequently such lengthy problems are set as can be answered by only those students who have solved them before with the help of their teacher. Usually the different universities have to select the examiners from out of the same set of people. There is a time limit within which the answer books have to be assessed, and the work has to be done in a rather mechanical manner. Little or no credit is given for a fair attempt. The system neither brings out nor helps to bring out talent. Mechanical thinking is all that this system is encouraging. The only merit of the system is its objectivity but the price at which this objectivity is purchased is really heavy. A large part of the university revenue goes towards the payment of examiners' fees, expenses of invigilation, printing of question papers and the like. This system was evolved as a means to an end and so long as the aim of education was to produce clerks and a few officers for the British bureaucracy in India, it succeeded really well. Whatever the system of examination may be, a brilliant student is bound to do well because he takes hardly any time in adapting himself to the system and learns the tricks of the trade readily. But the problem is whether the system brings the best out of the students. In my humble opinion the present system fails to do so. With independence our aim of education had to change and it has changed. We now wish to produce good citizens with a healthy outlook on life; thoughtful officers with a zeal for service of the people: great statesmen and above all productive scientists. We have produced some very good scientists even under the present system but considering the huge population of the country they are a rarity. We have, therefore, to see if we cannot change the present system for a better one and achieve our aim more quickly.
Trust begets trust. Our examination system is based on distrust of the students, distrust of the teachers, distrust of the examiners and even distrust of the persons engaged in the work of tabulation in the university office. If we are not able to produce honest citizens, our examination system is to be blamed for it to a very great extent. It is only recently that we have started associating the teacher with the work of assessment. But this is usually considered to be a concession and is done in a half-hearted manner. In ancient India no guru ever thought of an external examiner. A student's ability was judged by the name of the guru under whom he had received his education. It was the guru who was responsible for the moral, mental and physical growth of the students. In any good system of examination these three facets of development have to be kept in view. The present system has taken away much from the regard and respect in which the teacher was held. The students hardly bother about the teacher and much less for the real knowledge he imparts. Their main objective is to pass the examination, by any means fair or foul. If a teacher has something original to give the student tends to be inattentive thinking that what the teacher is doing in the classes will be hardly of any use to him in the examination. An original thinker among the teachers may be held in awe by the students as a very able person but for all other purposes he is considered to be useless.
“There was a time”, as Professor Shanti Narayan once put it, “when the teacher, the taught, and the examiner used the same book, and there was thus no particular difficulty in taking an examination”. With the multiplication of the number of good books on any particular topic, and more qualified teachers and examiners, everything has changed. The student tries to confine himself to the prescribed syllabus, the teacher will like the students to learn the original way of dealing with a subject which he himself may have evolved, and the examiners would like to ask questions which have interested them during their study of the subject. These may never have received the teacher's attention in his classes. The whole approach to the subject may have been different. Naturally students fail and there is a colossal wastage of human effort. The number of failures at the examinations is very large. At some examinations not more than thirty percent students pass by their own effort. To stop hue and cry, the results have to be modified and some sort of grace marks are awarded to the students to enable them to pass the examination. How much grace there is in these grace marks, it is rather difficult to say. Our education minister, M.C. Chagla has drawn pointed attention to this fact. If the wastage of human effort were due to high standards required for an examination, it would perhaps be excusable. The high percentage of failures at the university level has troubled Dr. Kothari10 as well and he has been drawing attention to it. The fact is that, in the present system of examination, only those students can do well who can successfully guess the sort of questions that could be asked in the examination. Some students who have worked hard for a little time near the examination and learnt facts and solutions to important problems from books or help books succeed while others who were giving a good account of themselves in the classes fail. The system does not encourage thinking, much less original thinking. It would not be wrong to say that under this system, many a Ramanujan remain unknown and die without making any contribution to human knowledge. If the teachers were trusted fully with the work of assessment, the state of affairs would be different.
An original thinker among the teachers may be held in awe by the students, but for all other purposes he is considered to be useless
In the United States, where the teacher is the sole judge, the students are able to learn much more and in a more thoughtful way than our students. There more stress is laid on the understanding of the subject than on memorising the facts. At many examinations the teacher permits the students to bring with them into the examination room books of formulae, and I see nothing wrong about it. At the campus of the Colorado University, where I taught last year, there were 12000 students. The classes had about 30 or 35 students in each section. The different teachers set their own question papers for their students. These were cyclostyled in the office of the department. No student ever attempted to find out what questions had been set. The question papers were never sealed. The teacher took charge of them directly; distributed them to his students at the time of the examination; collected the answer books; marked them within a couple of days, handed over the grades to the office; and there was the end of the matter. The university hardly incurred any expenditure on conducting the examinations. There was no delay in the declaration of the results. In fact, the degrees were conferred on qualified candidates within ten days after the examination.

In our system there is a lot of wastage of time and energy. For example in the Punjab, a student comes to us in the middle of July and is examined in the following April. He starts disappearing from the classes from the middle of February. He is thus with the teacher hardly for seven months in the year including the seasonal breaks and holidays. The examination results take no less than two months to be declared and there are many surprises for the teacher and the student both. During the time that the result is under preparation, the student is neither studying nor enjoying himself. His future hangs by a fine thread. Our rules and regulations are rigid and have no human touch. The rigidity is responsible for frustration in many cases. I have seen students failing by one mark or missing a first division by a similar margin. No system of marking can be perfect. It is hardly possible to decide if a student should get 32 or 33 marks – 32 may mean a failure and 33 a success. A student who has done well in three papers but has done badly in the fourth is required to take the whole examination over again next year. There are instances where a student has failed in one paper in one year and in another in the next – vagaries of examination. Again in our present system of examination, there are instances where the invigilators help certain candidates by smuggling in answer books. Year after year, a large number of students are disqualified for using unfair means. All this will stop if we make the teacher himself responsible for the assessment of the work of his own students and reinstate our ancient system of examination. If we start trusting the teacher, the students will be attentive in the classes, regular in their studies and better-disciplined. Teachers who are not devoted to their work will soon be discovered and will have to say good-bye to the profession. Cheap help books and “short-cuts to success” like “five minutes before the examination” will die their natural death. Our students usually confine themselves to the syllabus and hardly make any use of the library because the system does not encourage scholarship but cram work. If, along with making the teacher responsible for the class of students he teaches, we introduce the semester system in the universities and give credits for courses successfully attended, we can achieve much more than we do at present. Bright students could then cover their course and get their degrees much earlier than others. There would be no wastage of human effort. The strikes which are so common near the examination will, I am sure, be a thing of the past. Introduction of the semester system will enable us to invite to the universities, experts in different fields for courses which they alone can give. This will also facilitate exchange of teachers between universities. The standards of education and teaching will naturally rise. A trusted teacher will produce trustworthy students and the moral standards of the country will improve. For a little time that the teachers and students may take to adjust themselves to the new system there may be some sort of favouritism here and there. But as soon as things settle down, all will be well and for the better. Did we give up independence because it led to bloodshed for some time? For fear of a little favouritism, let us not delay the introduction of the system.
I have to warn you against the multiplication of universities in the country. There is a dearth of capable teachers all over, particularly of men capable of handling university classes and guiding research. Till we have the necessary number of teachers, let us devote our attention to developing the existing universities and institutions in the country. If we recruit young second rate teachers now, even brilliant people who may become available later will have to face frustration because they will be junior to people much less qualified but recruited at a time when really capable men were not available.
I must emphasise another point and it is that research and teaching should go together. We have a nice school of mathematics at the Tata Institute of Fundamental Research at Bombay. It can very well serve as a training ground for university teachers. Other centres are being set up at other places. If persons trained at these centres can take up teaching and research assignments at different universities even for short intervals and then go back to the centre, we shall be able to achieve what we shall never do otherwise.
Before I conclude, I regard it as my bounden duty and proud privilege as President of the society to thank Your Excellency for finding time from your multifarious engagements to come and inaugurate this conference. Your presence on this occasion will continue to be a source of great inspiration and encouragement to us and your good wishes will go a long way in making this conference a success. My thanks are also due to you, Mr. Vice-Chancellor, and Madras University for providing the venue and necessary funds for the Conference. Without your kind and close co-operation the arrangements could not have been what they are. The local secretaries and the volunteers also deserve my thanks for the pains they have taken to look to the minutest details in providing all comforts to the delegates and the members of the Conference.\blacksquare
Footnotes
- Editor's note: We record with deep gratitude the immense help we received from R.J. Hans-Gill and Madhu Raka in connecting us to the collected papers of Hansraj Gupta, photos and access to his original notebooks. ↩
- https://support.microsoft.com/en-us/office/weekday-function-60e44483-2ed1-439f-8bd0-e404c190949a ↩
- Editor’s note: Som Dutt Chopra was the first head of the department of mathematics of the Kurukshetra University. He passed away on 18 August 1997 at Kurukshetra, Haryana. ↩
- Editor’s note: For consistency and uniformity across the article, the Dr. and Prof. prefixes have been removed, and full name is given instead. ↩
- This photo is courtesy of Satish Bhatnagar, from the 1961 batch who is in the middle row standing extreme left. Seated to right of Hansraj Gupta is Ram Prakash Bambah.↩
- Editors' note: Alternative title mentioned by Hansraj Gupta in his communication [of the manuscript] with George E. Andrews was `My struggles in life'. George Andrews is an American mathematician, a leading number theorist famously known for his discovery of Ramanujan’s Lost Notebook. ↩
- Editor’s note: A former bronze Indian coin worth one sixty-fourth of a rupee. ↩
- Editor’s note: Rawalpindi was the capital of Pakistan from 1959 to 1969. The current capital is Islamabad. ↩
- Editors' note: This Presidential Address was delivered at the 29th annual conference of Indian Mathematical Society held at Madras from 27–29 December, 1963. Originally published in: The Mathematics Student 32 (1964), 121–126. ↩
- Editors' note: Daulat Singh Kothari was an Indian scientist and educationist. He was scientific advisor to the Ministry of Defence from 1948 to 1961. He was the chairman of the Indian Education Commission of 1964–66, popularly known as Kothari Commission. ↩
