Sophie Germain: Revolutionary Mathematician

Mathematics is often perceived as an objective, impersonal subject. A famous quote attributed to the philosopher and mathematician Bertrand Russell, reads “Mathematics, rightly viewed, possesses not only truth, but supreme beauty – a beauty cold and austere, like that of sculpture, [..]”. What allure does this seemingly lifeless discipline hold for the many who have spent entire lifetimes in pursuit of its truths? One insight into this mystery is offered through the words of a famous analyst, E.C. Titchmarsh. He says, “It can be of no practical use to know that \pi is irrational, but if we can know, it surely would be intolerable not to know.’’ In a similar spirit is this line by Virgil, from 29 BCE:¹ “Felix qui potuit rerum cognoscere causas’’ – Fortunate is one who is able to know the causes of things. This is the epigraph that Sophie Germain had attached to her prize-winning memoir submitted to the Institut de France in 1815.

Sophie Germain was a mathematician, philosopher, and also, a woman. Born in 1776, she lived in an era when women did not have the right to a formal education, especially in the sciences. Undeterred by these social and political difficulties, Sophie Germain made lasting contributions to mathematical physics and number theory. Her passion, courage, brilliance and perseverance are a source of inspiration even today. It is the life and work of this remarkable savant that is the subject of this book by Dora Musielak.

Sophie Germain: Revolutionary Mathematician is not merely a biography (neither is it a hagiography!), but a well-documented account of Sophie Germain’s life, the historical, social and intellectual environments of the age, along with an exposition of her mathematics along the way. The author has gone to great lengths to collect relevant papers, letters, photographs, and newspaper clippings, to the extent that reading the book creates an impression of strolling inside a Sophie Germain museum. This article attempts to give a glimpse of these (arti)facts.

Before delving into various facets of the book, let us familiarize ourselves with highlights from Sophie Germain’s life, as documented by the author. Sophie’s father was a silk merchant, classified among the liberal section of the society. In 1789, at the start of the French Revolution,² he was elected as a representative of the common people in the French court at Versailles, and later, was a member of the newly formed National Constituent Assembly. In constant contact with intellectuals, Monsieur Germain was perhaps a revolutionary himself! Sophie’s childhood progressed against the backdrop of violence, upheaval and change. It is not known if she attended a school or had a tutor. Nevertheless, neither would have given her a medium to learn mathematics as it was considered `improper’ for a woman.

Reading the book creates an impression of strolling inside a Sophie Germain museum.

It is believed that her father’s library was a sanctuary for Sophie during this time, a refuge from the turmoil outside. Her interest in mathematics is said to have been aroused by the story of Archimedes, who was so immersed in mathematics that he was heedless of the war raging around him and met his death at the hands of a Roman soldier in 212 BCE. It is apparent that this anecdote left a deep impression on Sophie’s mind. For, later in her life, when Napoleon’s armies were sent to occupy Prussia, she made a special appeal to the general of the Napoleonic forces to grant protection to the outstanding German mathematician and her correspondent, Carl Friedrich Gauss. Absorbed in his quest for mathematical truths, she was afraid that he may meet the same fate as Archimedes!

The foundation of École Polytechnique in 1794 brought about an unexpected opportunity for Sophie. Although women were not admitted as students or allowed to attend lectures and meetings, the scripts of the lectures were available in print in the Journal de l’École Polytechnique. At the end of each course, the professors would ask students to submit their observations. An Italian mathematician and one of Sophie’s friends, Guglielmo Libri mentioned in Germain’s obituary that on obtaining the notes for Joseph-Louis Lagrange’s course in analysis, Sophie wrote to Lagrange about her thoughts on the material, signing off as Monsieur Le Blanc.³ It is further noted that Lagrange praised her ideas and expressed his astonishment in flattering terms on learning her true name! There is no historical evidence to support this exchange. Nonetheless, Sophie’s identity became known in Parisian intellectual circles, with many offering books and other material to aid her self-study.

Perhaps one of the most popular anecdotes about Sophie Germain is her correspondence with the leading mathematician and astronomer of the time, C.F. Gauss. In 1801, Gauss published the Disquisitiones Arithmeticae, a creative and rigorous treatise on arithmetic, especially elementary number theory. Gauss’ observations have had a lasting impact on problems concerning the algebraic theory of numbers, which engage mathematicians to this date! In Sophie’s first letter to Gauss, written with the assumed name M. Le Blanc and dated November 1804, she conveyed her admiration for his work and included two proofs for a generalization of a result stated in the last chapter of Disquitiones. This demonstrates her mastery over not only the number-theoretic ideas involved, but also Latin, as Gauss’ text was written in Latin and no French translation was available until 1798. It is plausible that she studied Adrien-Marie Legendre’s Essai sur la théorie des nombres, published in 1798, which contained important results by Leonhard Euler, Lagrange as well as some discoveries of Legendre himself. Notably, the law of quadratic reciprocity, which was a result very close to Gauss’ heart, was recorded by Legendre in his Recherches d’analyse indéterminée in 1785.

In June 1805, Gauss responded to M. Le Blanc that he was very pleased with the observations and in particular, with his demonstration of 2 being a quadratic residue for primes of the form 8k \pm 1 and non-residue for primes of the form 8k\pm 3, although the approach seems to be an isolated instance and not applicable in general. Emboldened by Gauss’ reply, Sophie (posing as M. Le Blanc) continued to write to Gauss. In 1806, Napoleon’s armies invaded Prussia, bringing us to the incident described earlier. Commissioned by Sophie, an officer from the French army showed up at Gauss’ doorstep to ensure protection for him and his family. Baffled by the officer’s words, Gauss responded that he was not familiar with any French lady named Sophie Germain! It was when this confusion was brought to Sophie’s attention, that she wrote to Gauss divulging her true identity, clarifying that she was not entirely unknown to him and explained that she had borrowed the name of Le Blanc, fearing ridicule attached to the title of a scholarly woman.

Gauss’ response to her includes the lines which have now been primarily associated with their exchanges. These words encapsulate the singularity of Sophie Germain’s life in such beautiful and apt words, that it seems indispensable to reproduce them here:

The mathematical exchanges between Sophie Germain and Gauss continued until 1808, when we have the last documented letter from Gauss to Sophie, where he informs her of his move to join the University of Göttingen as a professor of astronomy and concludes by wishing her well. After this, Sophie wrote at least five letters to Gauss regarding her mathematical progress and ideas. It appears that Sophie never received a reply from Gauss, although he did send copies of at least two of his memoirs to her through his students. Be that as it may, it is certainly true that the correspondence with Gauss gave Sophie immense encouragement and confidence. The mathematical content of her letters has been well-researched and can be found in the article by Del Centina and Fiocca.⁴ One curious aspect that should be noted here is that although Gauss was a frontier figure in mathematical sciences at that time, he was, in fact, one year younger than Sophie!

The enchanting charms of this sublime science reveal themselves only to those who have the courage to deepen it

Sophie’s mathematical bent of mind won her the admiration of many in the community, but what she desired was professional recognition from fellow mathematicians. An avenue to gain the latter opened up before her in the guise of the Grand prix de sciences mathématiques announced by the Institut des France in 1809. This was a public competition, the topic of which was to develop the mathematical theory of the vibration of elastic surfaces, which explains the famous experiments of Ernst Chladni about vibrating plates. The deadline of the contest was set to two years later, in October 1811, and the prize was 3000 Francs. The panel of judges consisted of stalwarts such as Legendre, Pierre-Simon Laplace, Lagrange, Sylvestre Francois Lacroix, and E.-L. Malus.

Chladni’s vibrating plates were the cause of much excitement and awe since 1777. For a metal plate that is fixed at the centre and lightly sprinkled with sand, Chladni discovered that if its edges are strummed by a violin bow, then the sand particles get arranged in remarkable symmetric patterns. At the end of 1808 and the beginning of 1809, Chladni gave demonstrations of this mysterious phenomenon to the French scientific community and to none other than the emperor Napoleon Bonaparte as well! With the phenomenon being of great scientific as well as practical significance, the members of the institute had hoped that the competition would stimulate research towards the analytical theory behind these patterns. This challenge was believed to be a formidable one, with Lagrange supposedly commenting that the required mathematical tools in analysis were not yet developed.

This, however, did not seem to discourage Sophie Germain. She took upon the daunting task of deriving the mathematical equations that govern these vibrations, all by herself. Building on the work of Euler, Sophie worked towards formulating an appropriate hypothesis which would lead to the correct differential equation. Since early 1811, she found a patient guide and a favourable mentor in Legendre, who provided detailed and careful explanations of several parts of Euler’s memoirs. In October 1811, Sophie was the only one who submitted an entry for the contest. But alas, she did not win! Even though her hypothesis for the formulation of a partial differential equation was correct, the application of techniques from calculus had errors, and as noted by Lagrange, her equation itself was incorrect.

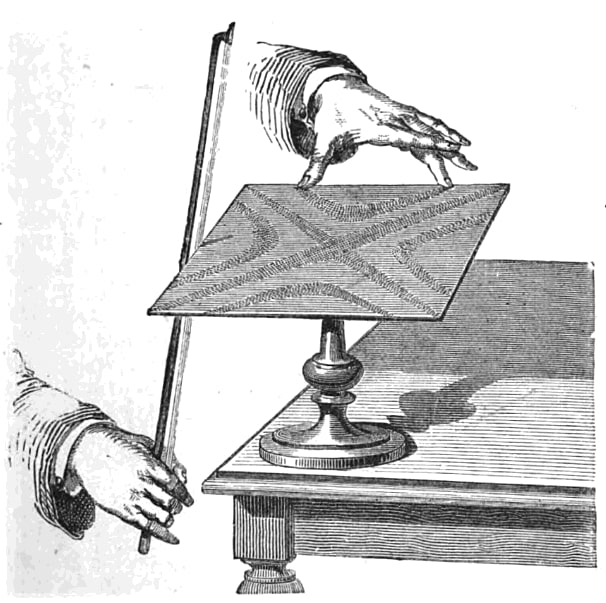
The contest was renewed a second time, with a deadline of October 1813. Once more, hers was the only entry! She now worked with the corrected version of her equation, provided by Lagrange. But she could neither solve it nor substantiate her claim with experiments. She received an honourable mention for her attempt. The competition was reopened once more, with an emphasis on supporting theory with experiments and a revised deadline of October 1815. The rules of the competition required entries to be anonymous, identified only by a short quote. For her third submission, Sophie chose the quote by Virgil that was alluded to at the beginning of this article. In December 1815, the panel decided that the sole entry in the contest was worthy of the award, and found that it was submitted by none other than Sophie Germain! This was a historic moment, as Sophie became the first woman ever to receive a major prize in mathematics. The award was to be conferred on her in a public meeting in January 1816, along with another prominent master of mathematics, Augustin-Louis Cauchy, who was awarded a prize for his work on wave theory. Alas, the audience that had gathered to get a glimpse of this unusual woman had to return disappointed as Sophie was not present for the meeting.

In the following years, Sophie kept herself well-informed about the progress in her areas of interest, even providing her own viewpoints. She also corrected and revised her prize-winning essay, and self-published a summary of her research on the theory of elastic surfaces. Expecting validation for her mathematics, she sent a copy of her manuscript to the newly renamed Royal Academy of Sciences. But what she received was either flattery (as in the case of Claude-Louis Navier) or copies of their own work (as in the case of Cauchy). The absence of a rigorous objective assessment of her work (in modern terms—a referee report!) was a major impediment to Sophie’s progress. Apart from her mentor Legendre and a sympathetic Joseph Fourier, she was compelled to develop her ideas in isolation. It is then even more commendable that she designed and performed experiments with very thin vibrating plates, without access to resources or laboratories. Today, there is consensus among several authors that even before Simeon Denis Poisson, Cauchy, Navier, and Gustav Kirchoff, Sophie Germain was the first to propose the formulation of a fourth-order partial differential equation governing the transverse deflections of a vibrating thin plate. The community had to wait almost a century for the general theory, until a Swiss physicist W. Ritz developed a method towards computing approximate solutions of operator eigenvalue problems and partial differential equations.

Apart from the theory of elastic surfaces, Sophie Germain made original contributions to the field of number theory, specifically in the context of Fermat’s Last Theorem. In the seventeenth century, Pierre de Fermat had noted in his copy of Diophantus’ Arithmetica that he had a marvellous demonstration of the fact that the equation x^n + y^n = z^n does not have any positive integer solutions for n \geq 3, but the margin is too narrow to contain the argument. This claim came to be known as Fermat’s Last Theorem and has captured the fancy of many mathematicians over centuries! Sophie was no different, and had communicated her wish to solve this mystery to Gauss. She had claimed in her first letter that she could prove Fermat’s assertion when n = p -1, with p being a prime of the form 8k + 7. In the same meeting where she was awarded the Grand prix des sciences mathématiques, the Academy announced Fermat’s last theorem as the topic of the next contest, with a submission deadline of 1818. Perhaps this challenge motivated her to renew her efforts! As we would now guess, none of the submissions of the contest succeeded in establishing Fermat’s claim and the problem was withdrawn in 1820. The enigma of Fermat’s last theorem continued to ensnare mathematicians and amateurs alike, until in 1995, when Andrew Wiles, along with his former student, Richard Taylor, were successful in proving the conjecture in complete generality. Their techniques relied heavily on mathematics developed earlier in the twentieth century, unavailable to Sophie Germain, and certainly beyond what was known to Fermat.

A proof of Fermat’s assertion in the cases when n= 3, 4 and 5 was known by 1825, with n=3 established by Euler, n=4 by Fermat himself and n=5 by Dirichlet. It was also clear that it is sufficient to prove the claim when n is an odd prime. This is because if n is divisible by an odd prime p, and n = pq, then x^n + y^n = z^n is solvable implies x^p + y^p = z^p is solvable, since a^n = {\left( a^q \right)}^p. However, the intricate and peculiar nature of the proofs of the above special cases made it apparent that a general method to tackle all exponents at once would be quite difficult. One of the first propositions that could allow one to deal with arbitrary exponents was proposed by Sophie Germain. She demonstrated that if for an odd prime p, there exists an auxiliary prime \theta such that

• p is not a p-th power mod \theta
• there are no two non-zero consecutive p-th powers mod \theta,

then in any integral solution to x^p + y^p = z^p, at least one of x, y or z must be divisible by p^2.⁵ To deduce the impossibility of integer solutions, her `grand plan’ was: given a prime p, find infinitely many auxiliary primes of the form 2Np+1 satisfying the second condition, which will lead to a contradiction! But alas, her plan proved to be futile, and she herself demonstrated its failure for p=3.

Sophie Germain made original contributions, specifically in the context of Fermat’s Last Theorem.

Nevertheless, her proposition leads to the non-existence of solutions in a particular case, namely, when p is such that 2p+1 is also prime and p does not divide xyz. This can be seen by an application of Euler’s theorem.⁶ Thus, primes p such that 2p+1 is also a prime came to be known as Sophie Germain primes. For instance, the numbers 2, 3, 5, 11, 23, 29 are Sophie Germain primes. These primes hold great interest for mathematicians of the modern day as well. We still have no proof of whether there exist infinitely many Sophie Germain primes! However, there is a conjecture predicting their density, which is a special case of the theme addressed by Dickson’s conjecture and Schinzel’s Hypothesis H. On the other hand, the companions to Germain primes, namely the prime 2p+1 corresponding to the prime p, are of utility in cryptography and pseudorandom number generation. Thus, we see that Sophie’s mathematics continues to be relevant even today.

In 1829, Sophie was diagnosed with breast cancer and, after a painful fight with a terminal illness, the remarkable mathematician bid farewell to the world in June 1831. Not long before her death, two of her papers were published in Crelle’s Journal, a testament to the fact that she sought refuge from the physical agony and suffering in the realms of the abstract and philosophical.

Dora Musielak’s book does justice to present a well-rounded and thorough picture of Sophie Germain’s mathematical pursuits, with the context of the historical revolution, the scientific developments and social circumstances of her time. Although the chapters are centred around events that take place in chronological order, the author has emphasised in the preface that such is not her intention. The repetitions arising from her choice of arrangement are crucial to maintaining a coherent flow of the narrative. Besides details about Germain’s life, the author includes background and mathematical exposition of the two significant problems that Sophie tackled: the theory of vibrating surfaces and Fermat’s last theorem. These discussions are accessible to a general audience while successfully communicating the depth of the mathematics involved.

She sought refuge from the physical agony and suffering in the realms of the abstract and philosophical.

The commentary on her life is often interjected with descriptions of the environment in France and Paris at that time. This emphasizes the fact that Sophie lived through perhaps the most tumultuous years in French history. She witnessed the fall of the Ancien Régime, the creation of the First Republic and the Reign of Terror, the rise of Napoleon to power, the Battle of Paris and the restoration of monarchy, the Hundred Days, the Battle of Waterloo and a second restoration of King Louis XVIII and finally, the second French revolution. This allows one to marvel at her dedication to know the causes of things, while being besieged by turbulent conflicts.

Several men of mathematics influenced Sophie’s journey. With Paris being a hub of science and mathematics, her paths crossed with some of the leading researchers of her time. This list includes Lagrange, Laplace, Legendre, Fourier, Gauss, Poisson, Navier and Cauchy, names that will surely be familiar to any undergraduate student of mathematics! Some of them were mathematical mentors, some sympathetic contemporaries, and some scientific rivals to Sophie. In Chapter 11, the author includes a brief account of their biographies and contributions, along with a note about their role in Sophie’s life. In my opinion, this chapter is crucial to painting a picture of the mathematical scene of the time, which enables the reader to connect with the content in the rest of the book.

Since Sophie herself did not maintain records, not much is known about her personal life and relationships. However, the author has made an honest effort to reconstruct parts of Sophie’s life and events, with ample evidence to support her claims. For instance, Chapter 7 discusses Sophie’s efforts to conduct experiments with thin vibrating plates to support her hypotheses. Although there are inadequate details available regarding Sophie’s experimental work, with the help of her letters and memoirs, the author recreates these experiments and describes how Sophie would have proceeded with them.

The chapter Pensées de Germain is dedicated to Sophie’s philosophical notions, with reference to her essays in which she argued the similarities between the creative process involved in science, literature and arts. In the penultimate chapter, the author records a plethora of questions about Sophie Germain, which still remain unanswered. History is riddled with examples of rare and impressive women who have established time and again that academics is not the monopoly of individuals of a single gender. The last chapter of the book includes a succinct portrayal of these figures, from Hypatia of Alexandria to Madame Paulze Lavoisier, wife and assistant of the chemist, Antoine Lavoisier.

The written correspondence between Sophie Germain and Gauss has intrigued many. The author, Dora Musielak, has translated nine of the fourteen letters exchanged between them and has included them towards the end of the book. These allow us to decipher the regard that Sophie and Gauss held for each other, be privy to their mathematical interactions, and appreciate the language which gives these formal letters a very personal touch.

In summary, Sophie Germain: Revolutionary Mathematician is an excellent reference for anyone yearning to learn more about the true persona behind a character, who, through her exceptional intellect and unwavering intent, was successful in leaving an impression on mathematics and history.

Two hundred years hence, the legacy of Sophie Germain continues to inspire admiration and reverence. The École normale supérieure de jeunes filles, a high school for girls, was established outside Paris in 1880. Closer to home, one of the first schools for girls in India was opened in 1848.⁷ Women working at the frontiers of mathematical research are seen in larger numbers today. Maryam Mirzakhani was awarded the Fields Medal in 2014 and Karen Uhlenbeck received the Abel Prize in 2019, becoming the first female mathematicians respectively to be honoured for their significant and impactful work. Even more recently in 2022, Maryna Viazovska became the second female recipient of the Fields Medal. Celebrating their mathematical accomplishments through workshops and conferences across the world, we have certainly come a long way since Sophie’s era.

On a personal note, I feel deep respect and gratitude towards courageous women mathematicians such as Sophie Germain, whose staunch and steadfast drive, and significant mathematical accomplishments paved the way for societal change, allowing women like me to be here today.

Acknowledgements: The author would like to thank C.S. Aravinda and the entire Bhāvanā team for detailed editing and insightful suggestions. She is also thankful to Ram Murty and Usha Mahadevan for helpful comments on an earlier version of this article.\blacksquare

Footnotes

1. Commonly referred to as Virgil, Publius Vergilius Maro (70 – 19 BCE), was an ancient Roman poet best known for the epic poem The Aeneid. ↩
2. As a period of political and societal change in France, the French Revolution was a series of developments that unfolded between 1789 and 1799. ↩
3. Andrea Del Centina, Letters of Sophie Germain preserved in Florence, Historia Mathematica 32 (2005) 60–75. ↩
4. A. Del Centina and A. Fiocca, The correspondence between Sophie Germain and Carl Friedrich Gauss, Archive for History of Exact Sciences, Vol. 66, No. 6 (2012) 585–700. ↩
5. The result which is usually attributed to Sophie Germain is the weaker version which was recorded by Legendre, that under the above hypothesis, at least one of x, y or z is divisible by p. The stronger version, proving divisibility by p^2, was later found in her manuscripts. See `Voici ce que j’ai trouvé’: Sophie Germain’s grand plan to prove Fermat’s Last Theorem, by R. Laubenbacher and D. Pengelley, Historia Mathematica, Volume 37, Issue 4 (2010), pp. 641–692. for details. ↩
6. Euler’s theorem states that for any positive integer n>1 and an integer a coprime with n, a^{(\phi(n))}\equiv 1 \bmod n. Here \phi(n) denotes the Euler totient function, which counts the number of positive integers less than n that are coprime with n. ↩
7. The school referred to here was started by Jyotirao and Savitribai Phule at Bhide Wada in Pune. Savitribai, who was herself educated by Jyotirao, is often regarded as the first female teacher in India. Today, the University of Pune has been renamed Savitribai Phule Pune University in her honour. ↩