
Still under the grip of the British Empire ruling India then, and international politics impacting every sphere of activity, the title of the essay may not have been too unseemly either. Harish-Chandra sets out exploring, from a historical perspective, the nexus between simultaneous pursuits of politics and mathematics, and discussing people in high places indulging in mathematics, right from the time of Aristotle, all the way up to the end of the First World War (WWI), concluding with the mention of mathematician and philosopher Bertrand Russell, who even served a six months’ imprisonment in 1918.
The essay was written shortly after the outbreak of the Second World War (WWII). While the full scale and costs of the war were yet to be seen, the conflict had already begun to have a constricting effect on academic mobility and collaboration. A case in point is that of Harish-Chandra’s later teacher Homi Bhabha, who came to India from Cambridge for his annual vacation before the start of the war in September 1939, but could not go back.
“My guess is that he wrote it after reading E.T. Bell’s book Men of Mathematics, which he gave me to peruse after one of our discussions on the history of mathematics”, surmised Harish-Chandra’s physicist daughter Premala Chandra upon reading the essay. The guess is supported by the close match in content and perspective between the present essay and Bell’s book. She further added, “He always said that he enjoyed this book very much.”
Quite interestingly, this book has had a telling impact on his close contemporary, and long time friend, Freeman Dyson who said:1 “The book that most influenced my choice of career was Men of Mathematics.’’ Elaborating on it, Dyson further added:
I think my choice of pure mathematics for a career was mostly the result of reading Men of Mathematics by Eric Temple Bell at the age of 13. I was doubly lucky, as Bell’s book was newly published in 1937, and it was given to me as a high-school prize by Winchester College. The book is a collection of mathematical biographies, bringing mathematicians to life as real people, and explaining their work with enough technical detail to bring their ideas to life.
Despite being recognised as historically questionable back then itself,2 Bell’s book still remains one of the most widely read and admired.
Momentous ongoings of the time notwithstanding, the essay by Harish-Chandra, engaging on its own, carries thoughtful ramblings of a young mind, still in teens, contemplating a pursuit of mathematics. We present it here with minor necessary edits, correcting the typos.
Mathematicians, Kings and Politicians
Talent is not an exclusive privilege of the rich, but sovereignty and political eminence are. And so it is not much too odd that we do not find many personalities, which have had in them both of these possessions together. As even a casual study of the past records would show, mathematical talent has a vicious fondness of evincing itself unexpectedly in men of poor lineage (perhaps much to the detriment of mathematical progress itself). True geniuses like Newton, Gauss, Abel, Cauchy and Riemann came from the soil.
Another probable reason for the extreme rarity of mathematicians, with active political careers, may be looked for in the nature of the science itself. It requires so much of meditative effort, with complete gathering up of one’s scattered self from all the distant realms of thought, that one is left with little time and still less space in mind for other thinking. Or perhaps, as a mathematician himself would put it, his pursuits are so engrasping3 that all other mental allurements (which he calls distractions) are enfeebled before this irresistible attraction. Another possible solution can be suggested on perhaps more pedantic grounds that any renown or prominence gained in pacifying or aggravating these mean disputes and ignoble clashes among men, is no honour in the eyes of the mature philosopher, exploring the mysterious region of abstract numbers.
That kings have not been interested in mathematics is again no wonder. Mathematics is not required to make a person a `gentleman’—with all the delicacy and elegance associated with the term and the objective of the instructors of a prince has always been to make out of him, first a gentleman and then an administrator and a soldier. A royal palace is the least congenial place for the mathematical talent to flourish. The errant talent, whenever it must akenly happens, to arrive in a royal family, is starred out unnoticed by the conventional mode of education. History, therefore, does not record instances where monarchs themselves did some creative work. However, quite a number of the ancient kings had learnt to value and patronise mathematicians as promoters of a particular form of philosophic learning.
Going back to the most ancient days, we find Aristotle, laying foundations of absolute logic, on which the tall edifice of modern mathematics stands. These remained unchallenged to our times, till very recently Brouwer4 was first to doubt the range of validity of Aristotelian logic, when used in conjunction with our concepts of the infinite. But Aristotle was a political philosopher too. Along with a thousand and one things whirling in his brain, he thought of the State and also of numbers. But he was an abstruse thinker rather than an agitating politician or a pure mathematician.
Archylas is another ancient specimen with such a combination. He was made seven times the governor of his city Tarentum, where he is known to have had much public prominence. He was, in addition, interested in geometry and invented various mechanical devices for constructing curves. He was the first to solve the problem of constructing a cube, double in volume to another. His solution depended on geometrical construction based on the intersection of the surfaces of a cylinder, a sphere and a cone.

Coming nearer to our times, there appears a remarkable man in the 10th century. His name was Gerbert. Brilliant from the beginning as he was, he had a deep interest for astronomy. He was especially known for constructing terrestrial and celestial globes, which excited great admiration among others. He became the archbishop of Rheims and was finally elected Pope when he assumed the title of Sylvester II. The rest of his life, he was involved in political affairs. His mathematical achievements include the solution of a remarkably difficult problem (at least for mathematicians of that age) of finding the sides of a right angled triangle whose area and hypotenuse are given. He gives the solution as \frac{1}{2}\{\sqrt{h^2+4a}+\sqrt{h^2-4a}\} and \frac{1}{2}\{\sqrt{h^2+4a}-\sqrt{h^2-4a}\} (where a is the area and h the hypotenuse), which is correct.
Among the few monarchs who have been interested in mathematics is Fredrick II of Spain. He did all he could, to spread in Western Europe, knowledge gained from Arab mathematicians. Though himself no creative mathematician, he did more than perhaps a mathematician could do for the promotion of the science in Europe.
Thomas Bardwardine was Archbishop of Canterbury, who played a prominent role in the invasion of France and the victory of Cressey. In spite of the political feuds between the church and the state he was actively interested in mathematics. He had been a teacher of the subject for sometime in Meston College, Oxford. His works concern with arithmetic, geometry and finding the area of the circle.
Nicholas Oresunus is another man in the fourteenth century, who has the proud distinction of playing with mathematics and also meddling with politics. He was the confidential adviser to Charles V of France and tutor to Charles VI and was finally made the Bishop of Lisieux. He was perhaps among the first to introduce the idea of practical indices.
In the fifteenth century Cusas’s name seems mentionable. Though coming from a poor family, he had a rapid rise in the Church and became a Cardinal. His mathematical writings deal with reforms in the calendar and finding the area of the circle. He however takes \pi = \frac{3}{4}(\sqrt{3}+\sqrt{6}).
The credit of the invention of symbolic algebra (if it can be assigned to one man), goes to Franciscus Vieta, a French mathematician, a lawyer and a public man of the 16th century. He was a member of the provincial parliament of Brittany, and was subsequently made master of Requests, at Paris. He zealously propounded the theory of divine right of Kings. His great work is comprised in In Artem Analyticam Isagoge, in which he anticipates Descartes in his application of Algebra to geometrical problems. He gave a Euclidean solution for the problem of describing a circle which would touch three given circles. He knew the expansion of \sin n\theta in terms of \sin\theta and \cos\theta, and gave 2\sin(\frac{\pi}{45}) as a solution of an equation of 45th degree proposed by a Dutch mathematician Romanus. His method of notation consisted in using vowels A, E, I for the unknowns and consonants B, C and D for the known. He gave a solution of the quadratic and cubic equation. His solution is as below.
First the cubic equation is reduced to the form x^3+3a^2x=26^3. Then, for x put \frac{a^2}{y}-y and we get and we get y^6+26^3y^3=a^6 which is a quadratic on y^3. Thus y and so x can be determined. He also solved the biquadratic equation in the following way.
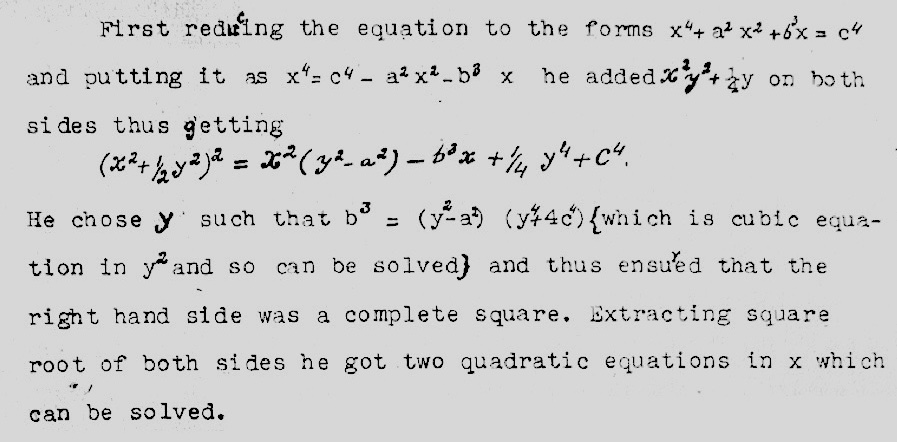
(x^2+\frac{1}{2}y^2)^2=x^2(y^2-a^2)-b^3x+\frac{1}{4}y^4+c^4.
He chose y and such that b^3=(y^2-a^2)(y^4+4c^4) (which is a cubic equation in y^2 and so can be solved) and thus ensured that the right hand side was a complete square. Extracting the square root of both sides he got two quadratic equations in x which can be solved. He also gave the value of \pi as equal to
\frac{1}{\frac{1}{2}\sqrt{\frac{1}{2}}\times\sqrt{(\frac{1}{2}+\sqrt{\frac{1}{2}})}\times\sqrt{(\frac{1}{2}+\sqrt{(\frac{1}{2}+\sqrt{\frac{1}{2}}))}}\times\cdots}which is correct.
John Napier, the famous inventor of logarithms, was an active participator in the political and religious controversies of the day. He strove to show that the Pope was antichrist. Besides the computation of logarithmic tables he devised mechanical instruments for division, multiplication and extraction of square and cube roots. Some of his work extended in special trigonometry also.
At the close of the period of renaissance, some contribution to mathematics was made by a Dutchman Simon Stevinus, Who was a close friend of Prince Maurice of Orange and was the Quartermaster General of the Dutch army. He enunciated the law of triangle of forces and solved the problem of finding the magnitude of the force, acting along the line of greatest slope, required to support a weight on an inclined plane. He also distinguished between stable and unstable equilibriums and deals in his book Statics and Hydrostatics with laws of fluid pressure.
Among men of political eminence who showed an aptitude towards mathematics and other sciences, the name Francis Bacon is outstanding. His political career culminated in his becoming Lord Chancellor and getting the title of Lord Verulam. He was in personal favour of Queen Elizabeth and was regarded as one of the wisest courtiers of the time. His chief work is Novum Organum, dealing with the fundamental principles to be kept in mind, when developing a scientific or mathematical theory.

Being satiated after some time with the social drolleries of Paris he decided to get a little mental peace by going to war, and he enlisted himself under Prince Maurice of Orange. Disappointed in his hope for action there, he hastened to Germany only to try another hand at soldiering under the Elector of Bavaria, then waging war on Bohemia.
Lying inactive in the winter quarters near the tiny village of Neubury on the banks of Danube, it struck to him, perhaps from the inspiration of a dream, that the application of Algebra to Geometry, analysis or more generally to any form of mathematical thought is really the most powerful method of investigation.
After engaging in some real fighting at Prague, and a triumphant march in Transylvania, he spent some time in Holland and then returned to Paris. Descartes again indulged in a bloody feud with the Duke of Savoy, in which he so distinguished himself that he was offered Lieutenant Generalship which he, however, refused. One discovery, which he made during his three years of meditation in Paris was the principle of virtual velocities.
He was living happily in seclusion at Eginoud when in 1646 Queen Christine of Sweden heard of him. After some reluctance he agreed to her wish of going to Stockholm and teaching her philosophy. Determined to make a Swede of Descartes, the Queen granted him an estate by a royal decree. There in Stockholm, he fell ill of inflammation of the lungs and died in 1650.
Apart from his metaphysical theories about the universe embodied in Le Monde Descartes greatest contribution to mathematics was his discovery of coordinate geometry. He invented the coordinates (known after his name) to fix the position of a front in a plane. The powerful implement invented by Descartes is responsible for the subsequent rapid development of mathematics. Some of his work also deals with the theory of equations.
Among the favourite disciples of Descartes was one Princess Elisabeth, daughter of Fredrick, the King of Bohemia. He is said to have declared “of all my disciples she alone has understood my works completely’’. Among other instructions in philosophy and mathematics, she was also taught this new, masterly invention of analytical geometry. She was another example of the rare freak of nature, when a mathematically inclined person is born in a royal family.
Perhaps, in the theory of numbers the French mathematician Fermat still remains unsurpassed in respect to the wealth of his contribution, made to this branch of mathematics. In addition to this he discovered the proposition that at the extreme of a given function f(t), f'(t) must be zero. His principle of least time in optics is quite well-known. Fermat was the first to extend analytical geometry to three dimensions. It was recently revealed in 1934 by Prof. L.T. Moore that Newton admits in one of his hitherto unnoticed letters that he got the hint of the method of the differential calculus from Fermat’s method of drawing tangents.
Fermat has stated all of his theorems concerning integers, without proof, sometimes however writing definitely that he had found one. However, all of them except one have either been proved or are still waiting to be shown correct or otherwise. He affirmed that if p is a prime and n an integer, then n^p-n is divisible by p. This was first proved by Leibnitz. Another theorem is that any prime number of the form 4n+1 can always be represented as a sum of two squares, and only in one way. Thus 41=5^2+4^2. Euler worked for seven years and finally established the proposition. Another curious theorem is that there is only one solution in integers of the equation y^3=x^2+2 (y=3, x=5) and no other is possible. After much labour, the proof has been found.

Fermat is an unparalleled arithmetician, but he was also a King’s councillor. In 1631, at the age of thirty, he was appointed in Toulouse as the Commissioner of Requests and in 1648 was given King’s councillorship, which position he filled with great ability and dignity for seventeen years. The exacting nature of his official work, together with his enormous contribution to, perhaps the most difficult branch of mathematics, casts a vivid reflection on the excessive fertility of his brain.
We are much too closely acquainted with Newton’s mathematical and scientific investigations to be told any more about them. What is perhaps required to bring him under the subject of this essay is the elucidation of his political actions, which have been so much overshadowed by his mathematical genius.
He was one of the delegates who went to London in 1687 to present before the court of the High Commission, case of the Cambridge University concerning the matter of granting a Master’s degree to a Benedictine, on the foolish insistence of the King and against the wishes of the university authorities. He was elected later in 1689 to represent the university at the Convention Parliament after the flight of James II. He sincerely performed his duty and did not seem to dislike politics. He was, as a matter of fact, responsible for keeping the disloyal elements in the University subjugated from rising against King William and Queen Mary, the successors of James. He was subsequently appointed Master of the Mint and there too he showed his ingenuity by introducing practical reforms.
Perhaps there is hardly a better illustration of a `universal genius’ (taken in the profoundest sense of the word) in history, than in the person of Leibnitz. He had a marked aptitude and a gifted talent for law, religion, political diplomacy, history, literature, logic and metaphysics. He shares with Newton the privilege of discovering the differential calculus, but what is more, is that he could also think of, along with this weapon to deal with the continuous, another to be applied to the discrete. He was the originator of what is now known as combinatory analysis, which when developed subsequently by Boole, Whitehead and Russell was to grow into a most useful instrument for logical reasoning. This branch of mathematical thought deals with an assemblage of distinct individuals, its object being to find any relations, which may subsist, in the most general case of complete heterogeneity. That Leibnitz had a most far reaching imagination is demonstrated by the fact that not till two centuries afterwards, the potency of the new invention was recognised. Now it is an indispensable instrument in the so-often used theory of probability, and is responsible for the entire development of the new quantum mechanics.
In 1666 at the young age of twenty he was conferred a doctor’s degree from the University of Altdorf on his brilliant essay on a new method of teaching law, and was also immediately offered the professorship of law in the university, however, he declined to accept. In the same year he published what he called a “Schoolboys’ Essay’’, De Arte Combinatoria in which was embodied his great creation, the combinatory analysis, which he predicted, would, when developed, reduce any form of mathematical reasoning to use calculation with symbols, thus eradicating completely any flaw due to imperfect logic.
Having done his real work at this early age the young man turned to something more practical and became, what can be best termed as a `commercial traveller’ for the Elector of Mainz.
The publication of his essay on teaching of law, brought him in prominence with the Elector and he was quickly being granted all varieties of important commissions. He, presently, rose to the rank of a significant diplomat and was partly responsible for the origination of the famous formula of `Balance of power’. Even Napoleon was disappointed at the discovery that he had been anticipated by Leibniz in his dreams to conquer and `civilise’ Egypt.
The later forty years of his life were spent in the inconspicuous occupation of being a librarian to the Duke of Brunswick—his work chiefly being to clarify and establish the much entangled genealogy of the family.
He and Newton were the foreign members of the French Academy. He was also elected a foreign member of the Royal Society of England.
As a diplomat he can be compared with any one of his times, being much more shrewd in his policies and controversies than perhaps all of them combined. He was really a rare specimen of a unique assemblage of varied talents.
Another great queen closely in association with the mathematician of her time and a great patron of mathematical learning was Catherine the Great of Russia. Euler, the greatest mathematician of the age, found a snug home in her court. She was responsible for providing him with considerable comfort and peace which made the huge and incessant output of his papers possible.
In a detailed political history and much more so in one of mathematics, the name of Laplace cannot be conveniently omitted. His great mathematical triumph was his successful discussion of the stability of the solar system, in which he took into account the complicated mesh of cross-pulls of the planets on each other. Only, when he was twenty four, he proved that mean distances of planets from the sun remain invariable except for slight periodic variations. For this brilliant achievement, he was conferred the honour of being the associate member of the French Academy.
After the French revolution, Laplace began his career as a politician. He had a strange knack of being able to please the government, whichever party was in power. He enjoyed Napoleon’s confidence, who made him minister of the Interior for some time. He was rewarded with a continuous succession of honours, being adorned by the Grand Cross of the Legion of Honour and the Order of the Reunion. He was also made a Count of the Empire. Then again, he was popular with Louis XVII who made him a Marquis and also the President of the committee to reorganise Ecole’ Polytechnique. Even his scientific and philosophic writings show a change in tone, in keeping with the current political vacations. In fact few people have been so successful in their diplomatic acts.
All the present network of complicated machinery owes its origin to the genius of a boy in the military school of Menzieri. Gaspard Monge, only when in his teens discovered a highly useful method in mechanical and military engineering called the method of descriptive geometry. It is a method for representing ordinary three-dimensional structures in a plane sheet of paper, every solid figure giving rise to two diagrams called respectively `plan’ and `elevation’. A short training makes an engineer feel as homely with these diagrams as with the mechanism itself. Other work of Monge is connected with differential equations and the investigation of curvatures of surfaces, his pioneer work in the latter preparing way for Gauss, in his theory of the geometry of surfaces.
Monge was dragged into politics by the great revolutionary swoop in France. He was compelled, against his wish, to be the minister of the Navy and the colonies after the revolution, and was put at the head of the Provincial Executive Council.
Monge’s career took another turn with the accession of Napoleon, to whom he was an intimate friend. He accompanied him in his campaign to Egypt, He, however, fell into disfavour with the government after the fall of Napoleon at Waterloo, and finally died in 1818.
Another great mathematician whose career has been much associated along with Monge’s, was Joseph Fourier. The natural eloquence of his stirring appeals had done much towards arousing the people for the revolution.

Fourier’s most important work is his theorem concerning the expansion of certain periodic functions under certain restrictions in terms of sines and cosines. Thus if f(x) is a periodic function such that f(x+\xi)=f(x) then
\[\begin{align*}
f(x)=\frac{1}{2}a_0+a_1\cos\left(\frac{2\pi x}{\xi}\right)+a_2\cos\left(\frac{4\pi x}{\xi}\right)+
\cdots+a_n\cos\left(\frac{2n\pi x}{\xi}\right)+b_1\sin\left(\frac{2\pi x}{\xi}\right)
+b_2\sin\left(\frac{4\pi x}{\xi}\right)+\cdots
+b_n\sin\left(\frac{2n\pi x}{\xi}\right)\end{align*}\](where the dots indicate that both the sets of terms are to be continued to infinity). Here a_n=\frac{2}{\xi}\int_0^{\xi}f(u)\cos(\frac{2\pi nu}{\xi})\;du, and similarly b_n=\frac{2}{\xi}\int_0^{\xi}f(u)\sin(\frac{2\pi nu}{\xi})\;du.

He joined the artillery of the `National Guards’, half of which organisation was composed of the liberal group, known as the `Friends of the People’. As a precautionary measure Galois was arrested, he being known as a dangerous radical. The government, after some manipulation, could find a charge against him. He was wearing, illegally, the uniform of the artillery, which had already been disbanded. In 1832 he was transferred out to a hospital due to cholera and was later released on parole. His half-broken heart was shattered by another unfortunate affair, in which he embroiled himself.
There is some mystery about his death but in a letter dated May 29, 1832 he writes to two unnamed friends, “I have been challenged by two patriots […] it was impossible for me to refuse. But my opponents have put me on my honour not to warn any patriot. […] Preserve my memory since fate has not given me life enough for my country to know my name. I die, your friend’’.

In the mathematical history of recent times, Paul Painlev is uniquely conspicuous for having the rare privilege of being a mathematician and a statesman, both of the first rank.
After taking his doctor’s degree he proved his merit and became professor of mathematics at Sorbonne. Shortly afterwards he was elected member of French Academie des Science.
The interest in politics he subsequently developed, resulted in his election as Deputy of Paris. His special interest lay in questions concerning army, navy and airforce. In Brand’s Cabinet 1915 he became minister of Public Instruction and later Minister for war. In September 1917 he himself became the Premier. He resigned in October but shortly again reconstituted his cabinet. After the Italian disaster at Caporetto he went to Rapaello to meet the Italian premier Orlando and Lloyd George, who had also arrived there. Their talks resulted in the selection of General Fosch as chief representative of France. He resigned in November only to resume his office again in April 1925.
His mathematical investigations are mainly concentrated on the theory of differential equations. The names of his most important works are Leçons sur le frottement and Leçons sur la théorie analytique des équations différentielles. His mathematical talent was recognised by the Royal Society of England and Academies of Science of France, Stockholm, Rome and many others, who elected him as their member.
Perhaps another man of interest from our point of view is Bertrand A.W. Russell. He is the author of The Principles of mathematics, his main attempt being to base all mathematical propositions on strict logic starting with a limited number of axioms. He is responsible, along with Alfred Whitehead for the extension of the mathematical logic of Peano and Frege. In 1910 the first volume of Principia Mathematica was published by joint authors.
He deviated towards politics when Mr. Chamberlain started his Tariff Reform campaign. He actively participated in the `No conscription fellowship’, on the outbreak of the war. He was sentenced for six months in 1918 for writing an article in Tribunal.
He wrote in 1920, after returning from a short visit to Russia, a book entitled the practice and theory of Bolshevism. He also published in 1919 Introduction to Mathematical Philosophy.

Russell’s assertion is that formal logic and mathematics are fundamentally identical and so he aims at the building up of the tall structure of mathematics on a few logical axioms. He has made significant contributions to the clarification of the problem of dealing with infinite sets as in Cantor’s theory of numbers. He succeeded in solving the notorious Paradox of the theory of Aggregates by means of the `Theory of Types’. He also put forth his `Axiom of Reducibility’ which, however, has now been practically abandoned. Thus politics and mathematics provide, perhaps (here in this case) equally fascinating fields for the play of the extraordinary talent of this philosophic thinker.
As mathematics and politics, with their growing complexities, are getting more and more unmanageable to be handled together, by even gifted men of rare intellectual talent, we might anticipate that these two realms of philosophic thought will ultimately be so far separated as to lose those binding links which nature has up till now been providing in the persons of great mathematical and political grants. Politics, as it is gaining a menacing dominance over all human affairs, might someday prove, even a disastrous enemy, to the less wordly science of mathematics. However, we should respect with the highest reverence, the memories of those who have been strangely successful in harnessing these two diverse and recalcitrant tendencies of human thought under the combining yoke of their talent and have been able to lead themselves on towards the enrichment of both of these spheres of mental action.
Harish Chandra,
B. Sc. II Year
(Maths. B.)
\blacksquare
Footnotes
- See pages 17–18 of the interview A discussion with Freeman Dyson, by Michael Th. Rassias, Newsletter of the European Mathematical Society, March 2020, pp. 17–20 https://www.ems-ph.org/journals/newsletter/pdf/2020-03-115.pdf. ↩
- For instance, see this 1938 review in the Jarbuch: https://zbmath.org/63.0793.03. ↩
- Though this word is not to be found in the standard dictionaries of English, it is clear as to what Harish-Chandra meant it to mean, and his usage seems interesting in itself. ↩
- Luitzen Egbertus Jan Brouwer was a Dutch mathematician who lived from 1881 to 1966. ↩
- For a fuller discussion see: Harish Chandra: Making of the mathematician, Bhāvanā, 6(4), pp. 5–22 (Oct. 2022). ↩
