Speaking the language of mathematics

It is a great pleasure to welcome you to this “in conversation” session with Bhāvanā. I thought we could start with my recollection of the first time I saw you. You visited India in 1988 for the Ramanujan birth centenary conference at the Tata Institute for Fundamental Research (TIFR) in Mumbai. The birth centenary year of course was 1987, but since Ramanujan was born on December 22nd, the conference took place in January 1988. It was a big conference and I was still a student then, and it was very inspiring for me to see in person the galaxy of mathematicians who had come: Jean-Pierre Serre, Atle Selberg, Robert Rankin, Wolfgang Schmidt, you, and many others. I still have vivid recollections of the event. One of the images I have is that you were accompanied by your parents. The image of Einstein flashed before me after seeing your father, though I haven’t met or seen Albert Einstein in person. So, let me begin by asking: Has anyone else said or mentioned resemblance between Einstein and your father?

DZ: I’m not quite sure. Certainly my father was short and Jewish, and had rather wild hair, and was very intelligent. I don’t know if he looked like Einstein. I don’t know how tall Einstein was. I’m five foot four, and my father was four inches shorter, with my mother and sister in between, so I was the giant in our family. My father, however, was much stronger.

Was that the first time you visited India along with your parents?

DZ: It was my first visit with them, and also their first visit. They had always planned to visit India, but somehow it had not happened. So they took advantage of the fact that I was going to India. I think I came twice more to India, and they came several times later and ended up visiting every part of the country, but if I remember correctly, that was my only visit with them.

On this occasion I stayed several weeks, attending two other Ramanujan centennial conferences and giving a course at TIFR.

But my first visit to India was much earlier. Probably the most famous conference at the TIFR for number theorists was the one that was held in 1956, where both Martin Eichler and Atle Selberg were there along with many other famous people, and both of them presented versions of what is now called the Selberg Trace Formula, so that 1956 is considered a historic date for the development of automorphic forms. There was then another conference held in 1979, somehow to commemorate the 25th anniversary of the earlier one. I don’t remember if Selberg was invited. I’m almost certain that David Mumford was there, but I’m not sure if Serre was. I also know that Pierre Deligne was there, as well as Barry Mazur, Hervé Jacquet of Jacquet-Langlands theory, Nick Katz, and many other people. It was a very high-level conference and I was terribly proud because I was not even 30 and was an invited speaker with all of these famous people. I gave only one talk, but ended up with two publications in the proceedings of the conference.² This is because I am a book lover, and was still young and inexperienced, and I assumed that papers in a book, especially one brought out by the TIFR, would be more visible than articles in journals, which seemed somehow more ephemeral. So since I was working on two papers that were both connected with automorphic forms and fit the conference quite well, I actually asked if I could send two papers and they said yes. The result is that two of the most important papers of my life are published in the proceedings of that conference, which therefore has a very big place in my mathematical life.³ That was my first visit to India, and I think that the Ramanujan birth centenary conference was my second.

First pages of the two papers published in the TIFR Bombay Colloquium on Automorphic Forms, Representation Theory and Arithmetic. courtesy:TIFR CAM

You mentioned that your parents visited India later several times.

DZ: They had at least three long visits of about four months each, so they cumulatively spent one year of their life in India. My mother in particular was very enamoured of India. She was a psychiatrist, and my father was many things rolled into one, but in particular, he had been a journalist and a political analyst for many years of his life. So he was very interested in different countries and their cultures. Both of them spoke several languages, many more in the case of my father. So they were both extremely interested in the world. But my mother was extremely interested in people and was absolutely fascinated by India. They travelled to every corner of the country, often in very simple ways—by bus, or in second-class coaches in trains—and usually either stayed in rather simple hotels or took lodgings in people’s houses, often then making friends with their landlords and later inviting them to Switzerland. So they had quite an Indian connection, much stronger than mine.

My mother in particular was very enamoured of India

That’s very interesting. I wanted to ask you about your childhood, and about your ancestral background.

DZ: It is complex. Both my parents had quite complicated backgrounds, but completely different. My father, David Zagier, was born and grew up in Poland, and he was Jewish as I mentioned. However, he was not a Polish Jew, but a Lithuanian one. Jews in eastern Europe identified themselves by where their ancestors came from, which meant which version of Yiddish they spoke, and my father’s family spoke Lithuanian Yiddish. He did not feel at all Polish, even though he of course spoke the language. If anything he thought of Poles as enemies, because it was an extremely anti-Semitic country when he was young. He was born in 1908, and so we are talking well before the two World Wars. Also, although I said he was born in Poland, that’s not really true. I don’t know how good your history is of that period, but there was no Poland in 1908!

Oh, is that so?

DZ: No, the country didn’t exist. After Napoleon, Poland was split up, with part of it going to Russia, and another part to Prussia. He lived in the Russian part. So when he was born he was actually a citizen of—well I don’t know if one could be a citizen as a Jew—but he was certainly a subject of the Tsar. (This was before the Revolution.) In 1916, when he was eight, the Germans invaded and conquered the region during WWI. So for two years, it was under German occupation; but of course, he wouldn’t have had a German passport. During that period the country in some sense belonged to Germany. Then when WWI ended, a treaty was signed and Poland was re-constituted as a country, and then he had a Polish passport.

I am telling his story first because it’s so complicated. Like many Jews at that time he lived in a traditional shtetl, meaning a small town with a large Jewish population, often outnumbering the Gentiles. As far as languages go, as a child, he spoke eight different languages. This was not because he was especially gifted for languages, although he was, but would have been the same for all the other Jewish children in his shtetl. All of them spoke Yiddish at home, and had to know Russian, German and Polish because those were the successive languages in which they were taught in school, and typically from the age of five they also began cheder, which is the Jewish school for children, and learned Hebrew and Aramaic there. These are related languages, but they’re different; somewhat like Italian and Spanish or French. The Torah (the Jewish name for the Pentateuch or Five Books of Moses) is written in Hebrew, while the Talmud (the compilation of biblical commentaries and religious law that is the central text of Judaism) is written in both Hebrew and Aramaic. By the way, Aramaic was also the native language of Jesus Christ, because it was the language of Judea at that time. Summing up, my father spoke Yiddish, Hebrew and Aramaic as well as Russian, German and Polish. That’s already six. And then in the village, since it is near the Byelorussian border, many people were Byelorussians, and many were Ukrainians. So he spoke those languages too, but of course, they’re both linguistically close to Polish and Russian.

As a result of knowing several Slavic languages from his childhood, when we later travelled in what was then Yugoslavia, we would stop in a town and there’d be a church with inscriptions in maybe three languages. He would read all three of them as easily as if they were English. We would say “Oh! We didn’t know you knew Slovenian, Croatian, or Serbian”. And he would say “I don’t even know which language I’m reading. However, I know that it’s a Slavic language, and I know what it says”. I mean, if you know four, you can triangulate and read others quite easily. He had no doubts, because every word and grammatical construction was familiar, even if he didn’t know which language it belonged to. So, that was his linguistic background.

The other thing about shtetls that you should know is that they ceased to exist after the war, because most of the Jews were killed during the Holocaust, and the ones who weren’t, emigrated. They went to America, some went to Israel. A few came back to Poland later, but the shtetl no longer existed. But when my father lived there it had not changed in style for 500 years. Everybody was extremely religious, very fanatical. They would have been horrified if they’d known that their son would eventually marry a non-Jew. But my father stopped being religious by the time he was, maybe, twelve; I think he had just seen too many horrible things.⁴ Nevertheless, after cheder, he went to a yeshiva, a Jewish seminary. You go to a yeshiva in order to study to become a rabbi. He did the entire course of study there until he was 18, and being good at Hebrew and Aramaic and able to interpret the Talmud and Torah intelligently, he passed the final exams easily, even though no longer being a believer and certainly not wanting to become a rabbi. But this was the only way he could get an education at all. So he went to Tachkemoni—one of the famous yeshivas of Poland—where rich Jews had instituted a few scholarships to support brilliant young Jewish boys who wanted to join a yeshiva but had no money to pay for it. My father got such a scholarship. That was my father’s background. By the way, the famous author Isaac Bashevis Singer went to the same yeshiva as my father, but I think he was two years older. I happened to meet Singer once briefly at a talk he gave in Yiddish, and mentioned to him that my father also studied at Tachkemoni.

My mother was 10 years younger. She was born in 1918. Everybody in my family was born in a country different from the one that they grew up in and the country they eventually lived in. I was born in Germany, but grew up in America and have lived most of my life in Europe. My sister was also born in Germany and grew up in America. She has lived for many years in England, but is an American. My father, as I said, didn’t move until he was 18, but then had a very adventurous life, with three further citizenships (British, American and Swiss) following the original ones.

mathematics is how my parents met! Maybe that’s why I chose mathematics later

Though my mother was born in London, her mother was Dutch and her father was Belgian. My maternal grandmother’s family was Dutch but she spent most of her childhood in England. At the end of the war she met a young soldier, who looked very dashing in his uniform and spoke Flemish, which is essentially the same language as Dutch. (The differences are mostly in pronunciation and some vocabulary, much like British and American English.) They were both happy to meet somebody who spoke the same language, and they fell in love and got married. It was not easy because he was a rather simple person—he later became the village policeman—while she had come from a sophisticated background: her father was a professor who had been invited from Holland as a Chair. She went to Belgium with her husband but was unhappy there and died very young, when my mother was only 17. So my mother was born in London, lived in Belgium until 17, and then went to America, where she learned English within one year, went to college, and then eventually decided to go to medical school. For this she needed one course in mathematics and my father was offering tutoring. So mathematics is how they met! Maybe that’s why I chose mathematics later, although I only realised this when I was maybe 30.

My father left Poland when he was 18. Even though he had no money, he managed to go via England to South Africa, and taught himself English, which became his ninth language. In Africa, he learned Swahili and Afrikaans as well. He lived there for eight years working as a journalist, and his English became perfect, certainly much better than mine. I would say both of my parents were extremely well read and knew every idiom in English, even though both learned it as adults. They both spoke better than I do, and way better than most educated Americans.

Anyway, my father became a writer and a journalist, mostly covering political events. Eventually, he could get a British passport and went to England, but then WWII broke out. He tried to join the war effort in England, but they wouldn’t take someone of his stature into the army, so he went to America, where he met my mother (through math tutoring, as already mentioned) and they got married. In just a few months, America joined the war over Pearl Harbor. To join the army one had to be a citizen. My father wasn’t, but if one was ready to join the Army and to fight, one could get citizenship immediately. So, he became an American citizen, already his fourth nationality. My mother, I think, was already one, as she’d been in the States for several years. My father eventually became an important counter-espionage officer, and he worked for the Office of Strategic Services (OSS) during the war; this was the predecessor of the Central Intelligence Agency (CIA). He served for several years in that line of business, but it ended in 1954 when I was three, because of the McCarthy period. People like him with strange backgrounds, born and brought up in strange places like Poland, were deemed suspects. In the McCarthy era, anybody who didn’t fit a certain description risked being accused of being a communist. And by that time he had risen to a very high position in the American secret service (now already CIA rather than OSS), so if it had been true that he was a secret foreign agent, it would have been the most serious infiltration in American history. Of course, it wasn’t true, and he exonerated himself; but this took over a year. Then for several years we moved every year, because he couldn’t get a proper job. That’s because he couldn’t say what he’d been doing previously, and that’s why as a child I moved every year.

I was in fact going to come to that, since you mention this fact in your interview with Mariana Cook⁵ where you say: “I moved every year for the first thirty years of my life”.

DZ: I was born in Heidelberg in Germany in 1951 although we weren’t Germans. We didn’t actually live in Heidelberg; we lived in Karlsruhe till I was 11 months old, but my sister and I were both born in Heidelberg. After the war, Germany remained free but was divided up into four occupied zones: American, Russian, French, and British. We were of course in the American Zone. Ostensibly, we were with the American army, but actually my father was working for the American government to set up an intelligence network in eastern Germany, which by then had turned Communist. He had to make some very high level decisions. When I was one year old we went to Japan where he was doing essentially the same thing, but now connected with China. These things, till 30 years ago, would have been completely secret, but this happened when I was a baby, and I’m now 71, and of course both my parents have died long ago, so I think there’s no need for keeping it a secret any longer, but that’s why I first lived in Germany and then in Japan. In America—I don’t remember all of it—we lived in Maryland, Virginia, Hawaii, Massachusetts, Tennessee, and California. I probably have got the order wrong, but we moved essentially every year because my father was looking for work. My mother always had work; she was a doctor, and had become a psychiatrist. That was in big demand, and so we could move and she would always find a job. My father kept looking and finally, in California, a wonderful friend helped him re-establish himself, and get a job as a teacher at a small college and a small university in Stockton, California. As a teacher, he taught English literature, creative writing, journalism, and political science. Finally, he had a new life.

Later on, my parents moved to Switzerland, and lived there for over 30 years, eventually becoming Swiss citizens. My father died in Switzerland, and my mother died in France. So, they had a very international life. My father is the only person I’ve ever even heard of, let alone met, who had five different nationalities in his lifetime, with each nationality having been held for many years. Even my mother had three nationalities: she was first Belgian, then American, and then Swiss. My father was first Russian, then Polish, then British with his Commonwealth passport, then American, and then Swiss, so he had five different passports in the course of his life. So that was my background. Very highly mixed and disrupted, in the sense that as a child, I moved every year. I did not suffer too much from this as I threw myself into studying and trying to get through school in a record time, but for my sister Vega it was quite traumatic. She nevertheless did brilliantly in school, finishing high school at the top of a huge class at the age of 16 and later going to medical school in Switzerland and becoming a psychiatrist like my mother. She now lives in London and works as an organisational consultant.

So that’s the complex story of my life, and my parents’ life. I don’t think one will often hear this kind of a story, especially my father’s life which was completely unique, but also mine, and because of the completely different background of my parents.

How old were you when you finished high school? Why did you choose to study at MIT, and what degrees did you earn there?

DZ: When I was a child, I was quite precocious. I finished high school at 13. By then my father had already decided on the next step. Actually he didn’t even consult or discuss with my mother. He was very bitter about the way the Americans had treated him, especially after he had served his adopted country at such a high level; his life was effectively destroyed. He had promised himself that he would stay there as long as the children were in school and not disrupt their schooling any more, but that as soon as Vega and I had finished school and gone on to university the family would move to Europe. So my parents moved to Europe, where I spent one year in school in England, in the famous Winchester private school. It was an amazing experience for an American kid like me to be in a 13th century school, and I believe I was only the second American that they had ever accepted then. Now they do have some foreign students, but not at that time.

A year later, I wanted to study in Oxford but I couldn’t because of their rigid rules. When I went to Oxford with my father to apply, they said that I couldn’t apply because they had an absolutely strict rule, with no exceptions, that they would not accept any student under 17 1/2, because they had had bad experiences in the past. So the only thing that I could do was to go back to America, and to MIT, where they didn’t care about your age—you could well have even been six, but as long as you passed their exams, and as long as you were good enough scholastically, you were admitted. Even Harvard wouldn’t admit me, because they had also had bad experiences, but MIT did take me. That was also why I did those two years quickly, because I was very young and my parents were 6000 kilometres away, and I wanted to quickly get back to Europe. The final joke was that when I came back to Oxford, this time to be a PhD student under the guidance of Michael Atiyah, I was still under 17 1/2 years old, but the age rule didn’t apply to graduate students and nobody checked anyway. I was too young to enter Oxford as an undergraduate, but I was able to join as a PhD student! So that was my revenge as it were, and a bit of the background why my childhood and schooling was so chopped up.

What was an early motivation for you to take up mathematics during your school going days?

DZ: It is like this. Kids who are very good at sports train for competitions or maybe for the Olympics. They don’t really even want to get a lot of money or become famous, but to find out and surpass what they can do, and take up the next challenge; they train for many hours a day just so that they can jump higher, or run faster. I was like that while going through school. I made a kind of a challenge for myself with each year that I skipped in school.

Actually, the first time, it was the school that came to my parents and suggested that I should skip a year. I was nine or ten years old, in fifth grade, and doing terribly: I wasn’t following the work, and I was failing every class, didn’t know what was going on, and wasn’t talking to anybody. I was quite a disturbed child, for reasons that you can easily understand. The school came to my parents with the results of the IQ tests. These were not just the quick ones where you answer a list of questions, but intensive tests given by the school psychologist. It had been thought that I was retarded since I was doing so terribly in school and showed no interest, but they discovered from the IQ tests that I actually had a very good mind. The school was appalled because it would look very bad for them if they had a smart kid who was doing so poorly. They went to my parents and said, “Your boy is actually very smart; maybe he’s just bored because of the courses,” though obviously the problem lay deeper than that, and said that if my parents wanted, the school would permit me to skip one year over Christmas, going from fifth grade straight into sixth. My parents made a fantastic decision. They didn’t tell the school yes or no; they didn’t tell me yes or no. They told me what the school psychologists told them, and said: “You remember those tests you took, it turns out you did very well. They said you’re very bright and if you want to go a year ahead you can do it, but it’s up to you.” They absolutely didn’t give me any indication of what they wanted, but simply said that it was my decision. I was about nine, and I made the decision. In some sense my life literally started on that day; before that, I have no memories at all. My entire childhood is blank. I don’t remember the houses we lived in, I remember almost nothing, less than what many people remember of their first two years.

My parents didn’t tell the school yes or no; they told me simply that it was my decision

My life transformed after that. I became very good in school. After another year, it was clear that I would have to skip again, and the school also felt the same. Later, I asked to skip several times, and the school allowed me to do so, but did not allow me to skip any courses. High school in America is always four years, specifically named freshman, sophomore, junior, and senior, but I wanted to do it in two years, and making that happen took a lot of trickery. For instance, you could have classes either from eight to two or nine till three; but you could also choose eight to three. That gave one hour more but that wasn’t enough, since I had to take twice the number of courses. I went to summer school each summer, but that added only a few more courses, and so I took correspondence classes as my father discovered I could do, to complete the required number of courses. I had to do all the exercises, and send everything to the teacher. But then they discovered a rule that one is not allowed to do more than 20 units by correspondence, which left me just a little short. I was desperate because now I had almost everything, but was still missing three or four courses that were needed.

My father, who was very inventive, discovered that in our town, Stockton, there were many people who had not finished high school and wanted to do so as adults. They were usually women who had dropped out because they got married when they were very young but were now 40 or so, with the kids out of school, and who wanted a job, maybe as a secretary, but couldn’t get anything without a high school degree. So there were special evening high school classes mostly geared for these women. These were not French, literature, philosophy or economics but rather in typing, shorthand and bookkeeping to prepare them for a secretary’s job. I am very short, as already mentioned, and at that time although I was already 13 years old and it was my last year in high school, looked more like I was nine, so I must have looked very odd indeed in a class where everybody else was a middle-aged woman and we were all sitting at old-fashioned typewriters with steep keyboards and learning how to type. I learned to type professionally like a secretary, and I could finally get my high school degree. This was a really crazy way to get through school, but very amusing in retrospect, and both the typing and the shorthand served me well in later years. But the main thing I learned was that it can be fun to work hard.

Absolutely fascinating! So is that how, for instance, you also developed learning so many languages together?

DZ: People who know that I’ve studied many languages sometimes say, “Well, you must be very gifted with them.” I am in fact reasonably good at them, but I know people who are certainly much more gifted. I think to do anything, like becoming a mathematician or learning languages, the main thing is that one really wants to do it. It’s much more a question of motivation than of talent. In my case, I grew up in America where I never heard any foreign language spoken, and none of my friends knew any, though we could learn a little bit of Spanish, French, and German at high school. But this was at a very low level, and not enough to really speak. I knew that my mother spoke four languages, Flemish and French from her childhood, and English; she had spent a year in South America, so she spoke Spanish as well, and later learned one or two more. My father, as I told you, spoke eight as a child, learned three more in South Africa; and then in Japan they both learned to get by in Japanese. Later, my father learned French which he hadn’t known, and they both knew German, but their common conversation language was always English and that was the only language I ever heard, except when they would occasionally say a sentence or two in French or German to each other so that the kids wouldn’t understand. Nobody I knew spoke anything except English. So although I knew that my parents spoke all of those languages, I had never really heard them. If you grew up anywhere in Europe, or in India, you hear many different languages, but I didn’t. And so somehow the idea of learning languages became extremely romantic to me.

I knew that my parents spoke many different languages but had never actually heard them, so learning languages became extremely romantic to me

We came to Europe when I was 14. I mentioned that my parents moved to Switzerland and that I went to school for a year in England, but then I had to go back to America. My parents stayed in Europe, so I saw them only during the summer vacations, and there my French, the language I had already liked in school, became fairly fluent because they were living in the French part of Switzerland. After finishing college, I lived mainly in Europe. I came as a third-year graduate student to Germany, and ended up staying there, so of course I eventually also became fluent in German, which I now speak with my wife. I started learning Dutch by chance because I saw a book in a second-hand bookstore in Oxford. Since it was my mother’s native language, I was curious to learn just a little bit and bought the book; but then I got hooked as I liked the language very much, and studied it more thoroughly.

the main thing I learned was that it can be fun to work hard

But how did you learn to speak Dutch from the book?

DZ: As I said, I saw this book Teach yourself Dutch in three months that was aimed at tourists and started reading it, and after I finished started buying books written in Dutch, so that after a year or so I knew the language fairly well for reading but couldn’t speak it at all. But later, a Dutch friend of mine was happy that I was learning the language and agreed to speak it with me even though his English and his German were perfect. Within a week, I could speak Dutch fluently, because I already knew all the words and grammar, but had never actually spoken it and didn’t know what it sounded like. By the way, there are other languages—Spanish, Norwegian, Swedish, or Catalan—that I later learned well enough to read a book and to have a reasonably good vocabulary and grammar, but that I have never learned to speak.

Later I started studying other languages, some for speaking and some just for reading like Spanish, and learned two others (Russian and then Italian) reasonably fluently. In the end there were quite a few others that I learned at different levels and it became a real hobby. I learned some Hindi, not at a very high level, but still not a complete beginner either, maybe the equivalent of a one-semester course in a modest university. My wife and I both studied Japanese fairly seriously, enough to read a book in Japanese slowly though never really progressing beyond the intermediate level, and we both studied some Korean and some Hebrew together, and I have also studied several other languages, like Turkish or modern Greek, at a very low level. I also started studying Chinese some four or five years ago after a visit to Beijing, and am enjoying it a lot.

I love studying languages and am absolutely fascinated by them, and the fact that in any two languages you express the same thought in different ways. It is not just that the words are different and that the grammar is different, but that you express the thought in a completely different way.

Could we now hear a bit about your Putnam experience during your MIT days?

DZ: It is a competitive exam. There is an amusing story that I’ll tell you that also shows how immature I was at the time. I was actually quite good at quizzes of that type. Already in California, I had won two prizes, one in chemistry—although I didn’t know any chemistry—and one in maths. That gave me some money, about a thousand dollars, which was enough to finance one semester in MIT at the time. And in my year in Winchester I had participated in the maths olympiad there and actually placed number one in the country, so that normally I should have participated the next year at the international level held in Romania, though this didn’t happen since I went to America instead, where at the time there was no olympiad. So when I came to MIT nobody had any idea that I was good in competitions.

to do anything, the main thing is that one really wants to do it

The Putnam is an exam that any university student can take, but also each university picks five students that they designate as their “team”. After the exams are graded, the results are published, but not completely: they only announce the names of the top five people but don’t say who finished first. They simply announce the top five, the next five, and so on, and a Putnam scholarship to Harvard is given to the person who got the highest score, or if they turn it down, then to the next person and so on. But they do give the ranking of the universities according to the sum of the scores of the five students whom that university selected.

Now to the amusing story. In 1966, I was 15 in my first year at MIT, and I knew about this exam as it was advertised everywhere. It’s a six hour exam consisting of 12 questions that is divided into two three-hour parts with a break in between. You could prepare a little by reading the questions of earlier years. It seemed to me that I might do well because I had looked at some earlier exams and many of the questions were easy for me. But the day before the exam I went to the library and looked at the previous year’s Putnam exam paper. It’s always set by one person, I think, and that person must have had a very different taste from mine. I don’t remember the questions, but they were very algebraic, and absolutely not for me. Out of those 12 questions maybe I could do six, and not terribly well. So I chickened out and didn’t go to the exam. Of course I know now that I should have gone anyway because if I didn’t like the questions I could have just walked out, but that never struck me because I was a kid, and kids normally don’t think to walk out of school if they don’t like something because the teacher’s eyes are on you. When I learned afterwards of the questions in that year’s exam, I could have kicked myself, because it was as if they had been written specially for me. I could answer half of the questions more or less in my head and could probably have done all 12 in an hour. So I would have had a very high score, but I hadn’t taken the exam because I had been too timid and too immature. After this experience, I of course signed up the next year in 1967 and I did very well (I think I got all 12 right, but with one question for which I had not given a very good answer) and placed in the top five, and in fact was offered the Putnam scholarship, though I decided to go to England instead. But the worst part was that instead of being happy about this result, the people at MIT were really mad at me for not having let them know that I was good at these kinds of competitions, so that MIT ended up looking silly because their team did relatively badly and they had failed to select the one student who ended up in the top five. And of course they were right to be mad; the fault was completely mine.

Hirzebruch’s way of explaining mathematics was perfect for me

Why did you choose to study at MIT?

DZ: As I said, it was mostly because they were willing to take me at 15, which Harvard and Oxford hadn’t been. When I got there I did a five-year program. It usually takes four years to get a bachelor’s, but you could do a double major in five, and I chose physics and mathematics. Everyone worked very hard at MIT, but I worked even harder, taking 128 units of courses one semester instead of the normal 40 to 45 units, and completed the five-year course in two years.

As I said, I was basically still a kid trying to surpass a record. I finished high school at 13, finished college with two degrees at 16, and later wrote my PhD thesis at 19.

Fascinating! Then you moved to Oxford, and from there to Bonn and studied under Friedrich Hirzebruch. What were the reasons for this move?

DZ: I started my doctoral studies in Oxford, but spent only two years there. Atiyah left after my first year as he was appointed a professor in Princeton. He eventually didn’t remain in Princeton and decided to come back⁶, but I didn’t know he would come back and was quite desperate. So I wrote to Hirzebruch in Bonn. I hadn’t done much research in Oxford as I hadn’t really found a topic, but I had read several articles by Hirzebruch and by Egbert Brieskorn, the famous geometer, and had discovered a small but quite pretty result, a formula involving cotangents for the signatures of the so-called Brieskorn surfaces. So I wrote a letter to Hirzebruch introducing myself, stating that I’d read his articles and his book Topological Methods in Algebraic Geometry, and that I was a student of Atiyah until he left Oxford. I asked if I could come to Germany and continue my studies with him. I didn’t need money as I had a small American scholarship of about \$1800 per year. Even in those days that was not very much but you could live off it in England and Germany. And I didn’t need to enrol in a PhD program in Germany because I had already satisfied the two-year residence requirement at Oxford to get a PhD.

I had to officially change from being a student of Atiyah to Hirzebruch, who became my official supervisor at the University of Oxford, even though he was physically in Bonn, and for this received a salary of £ 5 a year, because this had been the rate in maybe the 18th century and because Oxford is Oxford and they never change anything. Hirzebruch would joke about it and would use it to invite me to lunch once a year, saying: “Let me take you to lunch with my salary as your teacher!”

Was there anything specific about Hirzebruch’s mathematics that appealed to you as a student?

DZ: My time with Hirzebruch was very inspiring. He was a wonderful teacher and I was a good student. Atiyah had also been a very good supervisor but I had not been a good student with him because I wasn’t yet ready mathematically and his way of doing maths was very different. I had just read some papers with Atiyah, and was then essentially without a supervisor for one year.

Hirzebruch was an extraordinary teacher and his way of explaining mathematics was perfect for me. He loved teaching at all levels, and made a point of “accompanying” the same undergraduate students over several years, teaching them the beginning courses one year, then the second-year courses the next year, and so on. His lectures finished exactly on time and seemed very relaxed and even leisurely, with the available blackboards exactly and very legibly filled. He delivered his lectures at such a gentle pace, and in such an elementary way that his hearers often felt that they could have digested more, only to find that they had been given enough mathematical nourishment for weeks when they tried to go through the material in detail.

I was desperate by that time to do something, because after racing through the school and college years I had not made any progress for two years in Oxford. So I worked with great dynamism, and actually I found my thesis topic essentially by myself and finished within a year, returned to Oxford and submitted it where it was accepted. I had a kind of light-hearted bet with my father that I would get my PhD as a teenager. I didn’t quite make it, because I was 19 when I submitted the thesis but 20 when I actually got the degree as I had to go back to England for the defence and the degree ceremony was held only twice a year. So it was a joke in the family that I failed to get my PhD as a teenager!

Hirzeruch supervised the theses of over fifty doctoral students, including mine. When I arrived in Bonn in 1970 to work with him, I became part of a group of graduates and postdocs. It was a terrific group, but what impressed me above all was the way they did mathematics. They concentrated not only on their own research and on the problems that they could discuss with their supervisor, but also organized⁷ seminars on high-level topics they chose themselves, like spectral sequences or Spanier–Whitehead duality, and at which each participant was assigned some part of the theory to study in detail and to present to the others. It was impossible to go through such a training and not become a mathematician!

Hirzebruch loved formulas; he actually loved number theory and later switched to it. You’ll find these in an article in Hirzebruch’s collected works of which I suggested the title Reminiscences and Recreations, where he tells the story of how he moved partly to number theory from topology, and I always felt that this was partly under my influence, maybe starting with my cotangent formula, which was a piece of pure number theory related to Brieskorn’s work and involved some sort of Dedekind sums.

In my first year in Bonn, Hirzebruch gave a course on the Atiyah–Singer theorem, on which he was a big expert. It grew out of his signature theorem. He gave the course and I wrote up the notes, but I also did a lot of work and some of the things he explained were my work on the Brieskorn formula, so in the end it became joint work and was published as the book The Atiyah–Singer Index Theorem and Elementary Number Theory. Although I always feel that I collaborated with him, we actually only wrote two papers—one less important, and one quite important paper—and this book. The book was about number theory in topology and he writes fondly about it in his reminiscences. “More and more number theory in topology” became a slogan for him in his life from that time on, and also became very important for me.

It was impossible to go through such a training and not become a mathematician!

I also moved from topology to number theory, but that was different as I had never really liked topology: I became a topologist because it was the only thing you could study in MIT and Oxford at that time. Number theory was considered dead. People said, “Yeah, there were Hardy and Ramanujan, but that’s many years ago and also Vinogradov’s contribution to these things is 30 years old, and nothing new is happening now”. Whereas in topology they were making a breakthrough every year or two, like the h-cobordism theorem that was so exciting. The belief was that if you wanted to be a serious mathematician, you had to learn topology.

I met the two most important people in my life on the same momentous day

In my two years at MIT as an undergraduate there were no courses in number theory at all! This was because there was only one professor who taught it, Nesmith Ankeny, and he would give a cycle of four one-semester courses—elementary number theory, algebraic number theory, analytic number theory and geometry of numbers—every four years. Since students were normally there for four years, the idea was that every student could attend all four courses, although if they were very unlucky then they might learn the more advanced material in their freshman year and the elementary things in their fourth year, with a gap of two years in between. But my own two-year stint at MIT fell within the gap, so there was not a single course in number theory that I could take, even though that was the subject I would have most wanted to hear. Instead I was taking no fewer than five courses of topology in my last year because that’s all they offered. It was quite crazy, as I didn’t even want to be a topologist. But as I continued, I discovered nice concrete formulas, and they moved me towards number theory.

Hirzebruch moved the same way when we started collaborating. That was maybe the most exciting single thing in my mathematical life. In those four or five years after my graduate years, we really collaborated, in particular about Hilbert modular surfaces, which blended number theory and topology. When you’re very young, the feeling that you influenced your teacher, and not just the other way round, means a lot to you. One of the greatest things that Hirzebruch ever did—less famous than his signature or Riemann-Roch theorems but an absolutely brilliant piece of work—was his discovery of the resolution of cusp singularities on Hilbert modular surfaces. I had no part in that breakthrough, but his interest somehow arose out of our earlier work when we were studying what are called torus bundles over the circle and he realized that these occur as the boundaries of neighbourhoods of cusp singularities on Hilbert modular surfaces, which in turn eventually led him to find the resolution. The story is told briefly in the obituary article that I wrote about him in 2014, two years after his death.⁸

Apart from the mathematical impact, you mentioned that your first visit to Bonn changed your life personally as well?

DZ: I explained how I went from Oxford and Atiyah to Bonn and Hirzebruch. As for how it affected my life, Silke [Zagier (née Wimmer)], who is now my wife, was at that time a first year PhD student. She had finished her Masters, but at that time, in Europe and America one didn’t usually get a stipend for graduate work. I did have a stipend from the American NSF (National Science Foundation) but most people didn’t have one: if you were a graduate student, either your parents paid or you worked in McDonald’s or else at the university doing some academic job like grading exercises. She was working with Hirzebruch for the scientific organization of the new institute that he had just set up, called the Sonderforschungsbereich or special research centre. It lasted 15 years, and she was the scientific organizer for all of those 15 years; and when it ended and was transformed into the Max Planck Institute, she continued with essentially the same job as its scientific organizer until her own retirement in 2006. She eventually became interested in the history of mathematics but that was much later after she had retired.

Nobody really cares whether a prime is a sum of two squares or not. What we care about is that you can prove it

Before I went to meet Hirzebruch for the first time, I had read Brieskorn’s paper, and I had found a formula which I liked very much. It was a little like Ramanujan’s famous first letter to Hardy with its surprising formulas, although of course on a very much lower level. Hirzebruch had never seen such a formula before, and he immediately showed it to Brieskorn. Brieskorn was later a professor in Bonn but at that time he was a professor at another university and was visiting only for a few days. Hirzebruch wrote back to me and said, “ Why don’t you come on such and such a day, because Brieskorn, whose work you studied, will be there and you could meet him”. In fact, the three of us spent the whole afternoon together and in the evening when Hirzebruch went back home, Brieskorn, who was still single then and was in Bonn alone, invited me to dinner. But the person who opened the door for me when I arrived was Silke! So I met both Hirzebruch and Silke, the two most important people in my life, and also Brieskorn, who was also very important to me, all on the same momentous day.

So anyway, Silke opened the door, and led me to the office. She already knew about me. She later told me that Hirzebruch had shown her my letter a few days earlier: “Look, I got this very bizarre letter from this very young person. He’s a kid, but he’s found this amazing cotangent formula”. She still remembers today about the cotangent formula! So you can see how profoundly that day affected both my professional and personal life.

Going back to our earlier discussion about languages, was your fascination for languages natural?

DZ: Well, it’s surely natural for you also, and actually much easier for you than it is for me because you grew up in India and learned languages that distinguish many more consonants and many more vowels than English does, whereas I grew up in America, and Americans don’t distinguish anything. When it comes to Italian, one hears the difference clearly. I bet that your Italian is almost accentless; mine has a much stronger accent, because when one says a `t’ in French or in Italian, it should be non-aspirated. But if you’re German or American or English you say “tHu” instead of “tu,” and don’t even hear the difference. For many years, I didn’t even know. For instance, my French was already quite fluent, as I mentioned, but when I once asked a French friend what pronunciation mistakes I was making, he said, “Your nasal sounds are all right but your `t’ is terrible.” When I once mentioned this to Sameer, my friend and collaborator, he said that in Hindi and other languages they distinguish even more sounds; there are four T’s and four D’s, whereas in English we have only one of each and in Japanese even these are the same letter with only a distinguishing accent sign. So when people like you hear these sounds you automatically say them correctly because you can hear the difference, but I can’t, I have a terrible ear. For instance, when I studied Russian, I learned it well enough to give my lectures in Russian when I was there, but it was only later that a Russian friend whom I asked to help me with my pronunciation explained that there are two `l’s in Russian, a hard one and a soft one, but I had not learned to even hear the difference and hence could not reproduce it for a long time.

This was a side comment, and much too detailed, but I certainly love languages. I think this is because they’re very interesting and reflect different cultures, which I’m interested in because of my parents, but above all have a special meaning for me in that they are very mathematical in their structure, their accents, their rules, and their grammar. To me it’s very natural; and many mathematicians I know love languages. But many others have absolutely no interest. For instance Hirzebruch, my teacher, who had spent his postdoc years in Princeton, spoke English, but that was essentially all. He knew a little bit of French because he had it in high school, but he never had any interest in learning any others. On the other hand, Jacques Tits, who was a professor in Germany when I first came, spent years studying Chinese. He was Belgian, so he spoke French and Flemish and also English and German essentially perfectly. I know many mathematicians who love languages, and to me the most amazing thing is not why there are so many mathematicians who like languages, but why there are any mathematicians who don’t like grammar. Atiyah, for instance, even though he had the advantage that his father was Lebanese, so that he spoke Arabic as well as native English, and French quite well, only happened to know these languages because of his background but had no particular interest in learning more. But to me, it’s like a passion; of course I want to know other languages.

That’s true, a language is structured grammatically and somehow you can sometimes even speak conjecturally.

DZ: Yes, you can even invent a word, based on the rules. Of course sometimes it’s wrong, and then people will look at you strangely. When I first learned Dutch, I would often invent a word that I didn’t know, taking a German word and making a Dutch word out of it, pronounce it with the right ending and mostly it was right. When I got it wrong, they would say, “Hey you know, that’s German. We don’t speak German, we speak Dutch.” But they didn’t know how often I had used the same algorithm and produced the correct Dutch word without having learned it!

Learning languages to me is fascinating, even more fascinating if it’s a non-European language like Japanese or Hebrew because it is interesting to see a language that’s constructed according to different rules.

That’s absolutely right, that is personally my fascination also for languages.

DZ: There were several famous mathematicians who were extremely good linguists. The most famous was Gauss, who until he was 17 hesitated whether he would become a professor of philosophy or mathematics. It was only with his great discovery of the geometric construction of a regular seventeen-sided polygon that he decided that he would be a mathematician. But he loved languages to the extent that when he was about 60 or so, at quite an advanced age, he taught himself Russian, which is not an easy language, just out of curiosity and to see if he could still do it.

Much earlier, he learned English well too. Now every mathematician knows English, but not at that time. He of course could speak French and wrote in Latin, but English was much less natural. The story I read about him is that he would read, as they appeared, all the new novels of Sir Walter Scott which were the best sellers at that time. Once, he was so happy he found a mistake. Sir Walter Scott wrote “The moon rises broad in the northwest”.¹⁰ Gauss thought he should write a letter to Scott and explain that the moon never rises in the northwest; no matter how beautiful, it’s just not going to happen. Obviously I don’t know what Scott thought, but anyway, because of that story I know that Gauss didn’t just know English, he read novels in English for pleasure.

In more modern times, Andre Weil knew many languages, including Sanskrit, and also Russian. When he went to Russia, I was told, he also lectured in Russian and spoke it nearly perfectly, but he didn’t have friends who helped with the pronunciation and spoke as though it was straight out of a book, so that people said it was actually hard to follow because it was too formal.

It was Hamilton, I think, who knew Latin, Greek and Hebrew already by the time he was three. By the time he was eight, he had taught himself Arabic, Sanskrit, French, German and so on. I think he was famous for writing a letter in Persian to the Persian Ambassador when he was nine.¹¹ So there have been a few mathematicians in history who were incredibly keen on languages.

On the same topic of mathematics and languages that you mentioned, I don’t know whether it’s a systematic pattern, but other vocations which seem to go with mathematics are music and art. Perhaps you may reflect on it since you play the piano?

DZ: It is true that I love music, and it is true that I play the piano more or less every day. My wife is a natural musician, she is much more gifted. I grew up with music because my mother was a music lover. She had given up playing as a child, but she had a huge record collection and listened to a lot of music, and naturally the children would listen as well. When we were small she would even explain to us a bit, but that’s about it. As a kid I had to take piano lessons and I didn’t really enjoy them much, but my mother said, “You know, if you don’t want to learn, you can give it up, nobody is forcing you; but if you don’t give it up, you will be very happy and thankful someday that you kept at it”. I had faith in her, and so I persisted, and indeed it’s been one of the big parts of my life, pursued as a hobby. I love playing the piano, but I’m not a natural musician and don’t have a good ear.

For instance, I can only learn a piece of music by heart with great difficulty, while anybody with a natural ability just listens and then knows what to play. But it means a lot to me emotionally. I like it for much the same reasons as mathematics, because of the underlying structures. This is more obvious in the case of the music of Mozart or Bach, but even the much more romantic music of Brahms has a very complex structure, and it is that which makes it beautiful. Without the structure, with just beautiful harmonies and nice melodies, nobody would care. It’s because of the complicated changes in the rhythm and the harmonies that it comes alive. It’s deep, and is similar to mathematics. Nobody really cares whether a prime is a sum of two squares or not. What we care about is that there is a rule, and that there’s a beautiful and deep structure that lets you discover and eventually prove this rule.

You mentioned art too, but there I don’t really agree. I know many mathematicians who enjoy art, and who like to go to museums, and a few mathematicians who are very artistic, like my late colleague Yuri Manin, who painted beautifully, and I also know a few who do sculptures, but on the whole I would say that such a love is much rarer with the visual arts than with music.

I do agree, it could be much rarer. The reason I mentioned art is basically because I have researched some aspects about Harish-Chandra. He learned to paint at an early age, and his view of mathematics is that he thought of it in terms of art, as an empty canvas before you which can be filled without reference to external reality.

DZ: True. In the other direction an artist like M.C. Escher was extremely mathematical. But again, that’s very rare. I think there’s nothing mathematical in either Rembrandt or Goya, and it seems to be that if you’re a painter, especially a great painter, it’s not so much about structure; it’s more about how one visual element flows into the other. Whereas with music, I believe it’s very structured. The musician has to know exactly how a key change or a change of rhythm works. There’s a lot of theory, and you have to be aware of it. It’s very structured, much like the way the languages are, or the way mathematics is.

That’s right, even in literature, for instance poetry also has some underlying metric structure, I believe.

DZ: Well, poetry, I know mathematicians who appreciate it; Andre Weil certainly did. Manin was also an excellent poet, and I know a few more, but I still feel it’s relatively rare. Most of my mathematician friends are not poets. For me literature is not like poetry, it’s about the way the human story evolves, about the people, their stories, their characters, the way they talk. Whereas poetry is about the sound, the rhythms, where it’s much more like music.

“Speaking the language of mathematics” during the “Year of mathematics” in 2008 in the streets of Bonn. The person playing the cello is Matthias Kreck. MPIM Bonn

So, these vocations like music and poetry and so on, I guess they relate to mathematics on a certain level. In India, when I think of the first generation of mathematicians of the twentieth century, having no prior background of modern mathematical trends, and look at some of their own backgrounds, they usually trace back to music, Sanskrit, poetry or linguistic skills.

DZ: That does not surprise me at all. For instance, Manjul Bhargava, a good friend of mine, is very musical; and to him, I know, it’s very important. He’s a mathematician at the highest level in the world, and even before his Fields Medal I knew him as an unbelievably talented mathematician, but he is also an exceptionally good musician; music is terribly important for him. It’s not just like a hobby, he really cares about it a lot, and spends a lot of time thinking about it, as well as Sanskrit.

Returning to mathematics, you started off studying problems in geometry and topology, but number theory has since long been the centre of your focus. While you mentioned it earlier in passing, can you elaborate on how much of this is due to Hirzebruch’s own shift in interest from topology to number theory?

DZ: As I already told, the influence for this shift was partly the other way around and arose from my cotangent formula and from his course on related matters that then turned into our joint book on the Atiyah–Singer theorem and elementary number theory. The idea was to use these very sophisticated things like the index theorem and its equivariant generalizations, and then when you apply the general theorems to specific manifolds the equality of the left-hand and right-hand sides sometimes gives some very concrete number-theoretical statements involving things like Dedekind sums or special values of L-functions. These formulas can usually also be proved in more elementary ways, but the connections with topology and index theory make them much more interesting.

Excellent. I wanted to ask you about modular forms, which is one of the recurring themes in your work. What are modular forms?

DZ: A modular form is a mathematical object with two faces, a visible one and a hidden one. The visible face is what is called a q-series, which is an effective way of writing down a sequence of numbers that one is interested in. For example, instead of writing the values of the partition function as a list p(1)=1, p(2)=2,\,…, one can give the same information in the form of a q-series:

P(q)\;=\;q + 2q^2 + 3q^3 + 5q^4 + 7q^5 + \cdots\;.This q-series, which was already used by Euler, turns out to be essentially a modular form.

But the beauty of the theory is that there is also a hidden side, and that the modularity, which cannot be seen in the q-series, implies deep properties of the coefficients.

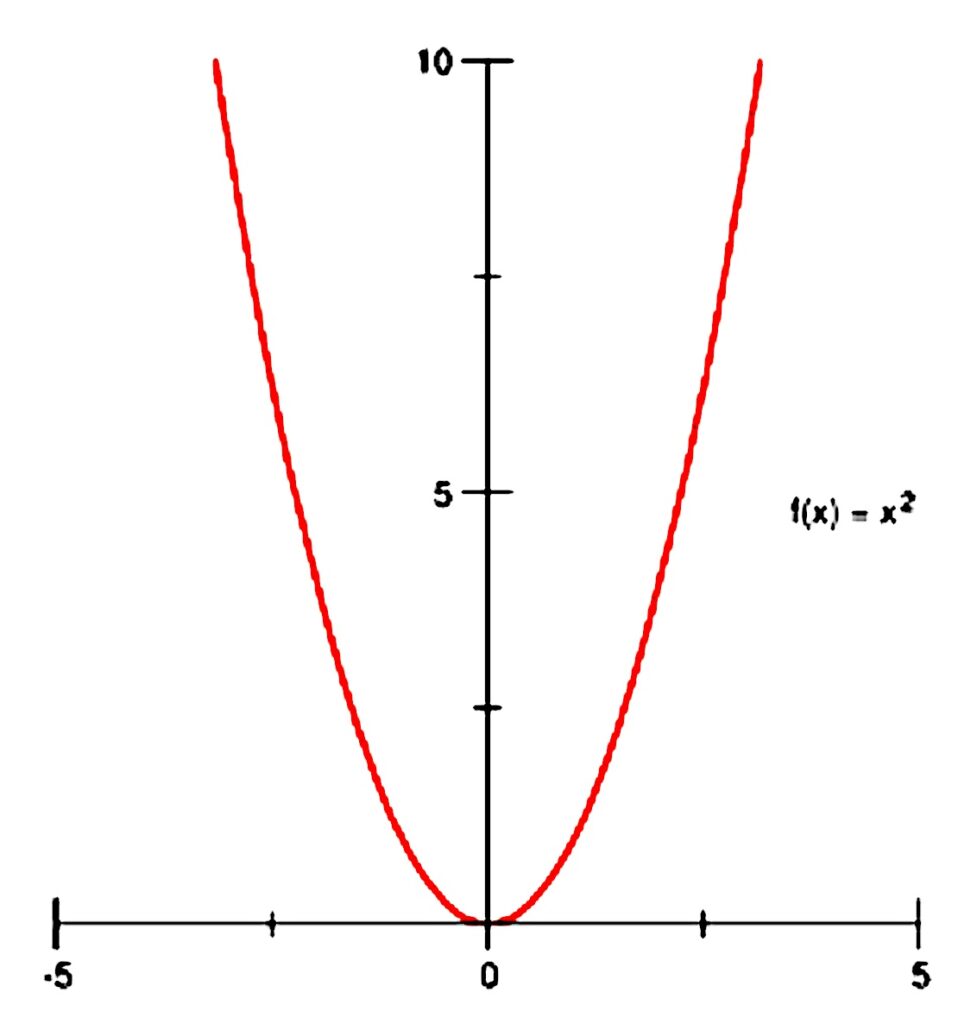
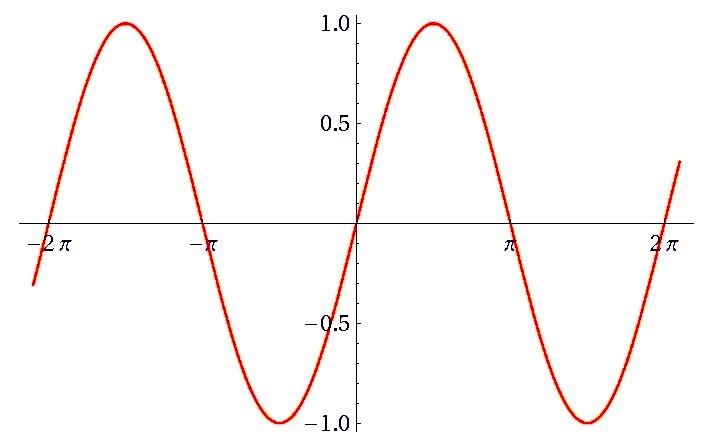
A modular form is a function having a remarkable type of symmetry—not just a simple symmetry of order two like the reflection of a parabola in an axis that you come across in school (image (a)), or even the slightly more sophisticated symmetry of infinite order given by shifts that you see in the graph of the function \sin(x) (image (b)), but rather an infinite symmetry of a much more subtle kind, called non-abelian, which is best illustrated by the drawing of Escher (image (c)). If our q-series is a modular form, then this hidden symmetry has deep consequences for its coefficients, and in many cases means that the most difficult-seeming formulas essentially prove themselves.

So the two key aspects of modular forms are: (1) They are formal q-series with arithmetically interesting coefficients, and (2) They have a hidden, non-abelian symmetry. The “magical principle” of modular forms is that each modular form has a kind of “fingerprint”, consisting of a list of computable invariants—specifically, its “weight”, its “level”, and a sufficient number of terms of the q-series—and that these invariants fully characterize them, so that if two modular forms have the same invariants, they are identical. Of course this magical principle would not be of any value if there were no mathematically interesting q-series that are at the same time modular forms. Happily, however, this is far from the case. Let me give you the names of a few q-series whose modularity one either knows or suspects, and for each one the arithmetic meaning of its nth q-coefficient:

(a) Euler’s q-hypergeometric series P(q)\,: the number of partitions of n

(b) Theta series: the number of representations of n as the sum of k squares

(c) Eisenstein series: the sum of some power of the positive divisors of n

(d) q-series of elliptic curves: the number of solutions of certain congruences modulo n

(e) q-series of Galois representations: prime decomposition of n in a number field

I can’t describe all the technical terms here. Perhaps it is illuminating enough to tell you that Andrew Wiles’s proof of the celebrated Fermat’s Last Theorem is a corollary of the proof of modularity of the q-series mentioned in (d). Similarly, the splitting problem in number fields, mentioned in (e), is a central problem of algebraic number theory, and is resolved essentially only in the few cases when the q-series in question are modular.

Why is a modular form thought of as an elementary arithmetic operation? And why are they important?

DZ: Modular forms of course aren’t really the “fifth operation of arithmetic”; this is just a famous bon mot attributed to Martin Eichler. I think it’s really true that Martin Eichler said it or wrote it somewhere. But I recently gave a special course of lectures for students in Lyon and Etienne Ghys, who is a very famous mathematician and is now the head of the French Academy, wrote a whole page article in Le Monde which has my name, not Eichler’s, in the title: Don Zagier and the five operations on integers.

In that article, he tells that I worked with the students and asked some questions about a certain problem about a cycle of period 9. I will tell you the problem first. Actually, there were two such problems, superficially quite similar-looking, with periodicities of order 5 and 9. One is about a sequence of numbers with the property that adding 1 to any number in the sequence gives the product of its left and right neighbours. The conclusion is then that the sequence repeats itself at every fifth step! For instance, if one starts with 1 and 3, then the sequence is: 1,\,3,\,4,\,5/3,\,2/3,\,1,\,3,\,…. The other is about a sequence of real numbers such that the absolute value of each number in the sequence is the sum of its two neighbours. The theorem you have to prove is that this time the sequence will repeat with period nine. Whatever numbers you take, the surprising thing is that the sequence repeats after the ninth step. You can try it out. It always works.

As to why modular forms are important, nobody really knows why something is important

I showed that to the students, saying that when I first saw it I didn’t even know why it was true, and that it was only some years later that I looked again and wondered, and gave a proof. I challenged the students: can any of you find a proof? This was on a Saturday. Then two students came to me the next day and they had found a proof. Actually, it was three students and two proofs: in one case one student had found half of the proof and a second student had completed it. Etienne Ghys, in his newspaper article, embellished the story a little, saying that there were five students who solved in one evening a problem that I had not been able to solve for three years, showing how excellent the students at the Ecole were! Anyway, it’s a nice article, and fun to read. He describes me as `a tad eccentric’, which is certainly true and sounds better in French than in English.

Coming back to why modular forms are important in mathematics and in physics, I would say: nobody really knows why something is important. But a modular form is something which belongs to two worlds and gives a bridge between them. It’s an analytic function with analytic properties, studied using analytic things coming from the theory of Riemann surfaces and complex functions of one variable, but at the same time it has an expansion with integer coefficients, and hence belongs to arithmetic. Of course, the cosine function also has a Taylor series expansion, but here the coefficients are very boring—just one over n factorial. But for modular forms, the coefficients can be much more interesting numbers; like, in how many ways you can write an integer as a sum of six squares. That is a non-trivial problem, but we can solve it completely because if you take the corresponding q-series, it’s a modular form.

So even though modular forms belong to the subject of complex analysis and the theory of functions of one variable, their applications are completely in number theory and combinatorics, because their coefficients are numbers that solve very interesting problems that one often cannot attack in any other way. For instance, both the partitions of numbers that Hardy and Ramanujan (and later Hardy and Littlewood) studied and the thing that made Wiles famous when he finished the proof of Fermat’s Last Theorem (FLT), give rise to modular forms. It was the French mathematician Yves Hellegouarch who discovered that there is a connection between FLT and statements about elliptic curves, and the specific thing that Wiles proved was what is called the Taniyama-Weil conjecture. In a few words, this says that “any elliptic curve is modular”.

An elliptic curve is a curve in the (x,y)-plane defined by a cubic equation of the form y^2 = x^3+ax+b where a and b are constants such that 4a^3+27b^2\neq0 (this condition ensures that the curve has no cusps or self-intersections), and the theory of such curves is one of the most beautiful in mathematics because of its depth and the variety of its connections with other areas. The conjecture that Wiles proved (with some assistance by Richard Taylor, and building on earlier work of Frey, Serre, and Ribet) says that whenever a and b are integers one can find a parametrization of such a curve in which both x and y are modular forms, after which one can apply the deep machinery of modular form theory to prove otherwise inaccessible properties of the equation.

The Taniyama-Weil conjecture is now seen as just a very special case of what is called the Langlands program, which is about special Dirichlet series called “L-functions”. (A Dirichlet series is a function of a complex variable s of the form \frac{a_1}{1^s}+\frac{a_2}{2^s}+\cdots, where the coefficients a_n are complex numbers.) There are two huge classes of such L-functions in modern number theory. One comes from algebraic geometry, from counting solutions modulo a prime number of some Diophantine equations like the equation of an elliptic curve that I described a few moments ago; and the other comes from modular forms and their generalizations, which are called automorphic forms. The Langlands program is essentially to show that these two classes coincide, giving a deep connection between seemingly unrelated objects from different parts of mathematics. One of the main thrusts of much of modern mathematics, and many of the Fields Medals from recent years, is about proving various parts of the Langlands program.

We would like to hear about how your famous collaboration with Benedict Gross came about.

DZ: We had already known each other for some years and had written two smaller papers together, but the “famous” collaboration was the one related to the conjecture of Birch and Swinnerton-Dyer, one of the seven million-dollar Clay Millenium problems, which finally culminated in a nearly 100-page long paper in Inventiones Mathematicae. Gross is a more creative and more original mathematician than I am, and the idea for this paper was completely his, based on some early ideas of Bryan Birch. I had certainly never thought of it and didn’t even believe at first that it could work, and he had some trouble talking me into embarking on the venture. Basically he needed to compute two L-functions, and he said I knew more about them than anyone else, which was probably true at that time, and he challenged me to do the computation, which was incredibly complicated. The way he tells the story, and I certainly don’t doubt it, is that when he described the problem to me and I was reluctant to begin, our common friend Stephen Kudla, who attended the discussion, said, “Don is just afraid”, and that did the trick!

After that we spent a week of anguish, spending days and days calculating different terms of each side of the equation that we were trying to establish. He later said that he’d never seen so much mathematics go by so quickly. After five days I had a formula containing 17 or so terms, each of which I had tested on the computer. One of the trickiest points was that I insisted on introducing a new parameter k (the “weight” of the modular forms being used), because the calculation is technically easier if k is bigger than one; even though for our application we only needed the case k=1. But many of the terms were given by infinite sums that diverged in that case and hence didn’t even make sense, whereas for larger values of k everything was convergent and therefore at least rigorously defined. But then Gross pointed out that there was one main term that made sense even in the k=1 case, and I started the computer. It was late in the night and he went to bed, whereas I’m a late night person and stayed up till four in the morning and did endless computations on my small handheld computer. By the next morning enough of the needed terms had matched up numerically that we were sure that everything would work out, and indeed in the course of a few more days it all did. So even though the whole original idea for what had to be proved was completely his, the skill in calculation was also crucial and that’s my forte. The whole thing was amazing, they were exciting moments.

The Birch–Swinnerton-Dyer conjecture appears in the million-dollar problems list of the Clay Mathematical Institute. Would it be possible to say something about it in accessible terms?

DZ: I already explained what elliptic curves are and how they are related to modular forms. The basic question, which in some cases goes all the way back to Diophantus in the 2nd century A.D., is when one can solve a given Diophantine equation, meaning an algebraic relation among rational numbers. For the case of elliptic curves, this means that given two integers a and b, we want to find rational numbers x and y satisfying y^2=x^3+ax+b. The Birch–Swinnerton-Dyer conjecture gives a complete prediction for when this will be possible.

Let me illustrate what Diophantine equations are by mentioning three examples from classical number theory: (1) Which prime numbers can be written as sums of two rational cubes (that is, cubes of rational numbers)? (2) Is there a right triangle with integer side-lengths a, b and c, where c is the hypotenuse, such that both a+b and c are perfect squares? (3) Does the equation a^n+b^n = c^n have any positive integer solutions for n > 2?

Diophantine problems of this sort have played a significant role in the history of mathematics. In particular, Question (3) is the problem posed by Fermat and famously known under the name Fermat’s Last Theorem, that was eventually solved by Wiles using modular forms, but the equation itself is not an elliptic curve. On the other hand, both problems (1) and (2), going back to Sylvester (18th century) and Fermat (17th century), respectively, are elliptic curves and in both cases the BSD conjecture predicts completely when there is a solution.

The startling thing is that different types of Diophantine problems have very different degrees of difficulty, and can be very different also from both the theoretical and the numerical points of view. For question (1), for example, if we take the prime number to be 13, then it can be written relatively simply as a sum of two cubes by noting that 13 = \frac{351}{27}=\frac{343}{27}+\frac{8}{27}=\bigl(\frac{7}{3}\bigr)^3+\bigl(\frac{2}{3}\bigr)^3. But try as you will, the prime number 5 cannot be expressed as a sum of two rational cubes, while for yet other primes there is a solution but it is huge and very hard to discover. The simplest solution for the “French revolutionary” prime p=1789, for instance, represents this number as the sum of the cubes of the two rational numbers \frac{38119538057820221}{2828707454055574} and -\frac{24606633997841365}{2828707454055574}, but this cannot be found even using a computer without using deep theory.

this cannot be found even using a computer without using deep theory

Why are the degrees of difficulty of these problems so different? It turns out that all diophantine equations can be divided into three classes, rational, elliptic, and of general type. Roughly speaking, they correspond to equations of degree 2, 3, and \geq4, respectively, although some exceptional degenerate equations of degree 3 may be of rational type, and some of degree \geq4 can be rational or elliptic.

The problem of finding rational solutions turns out to be “easy” for the first class, “hard but attackable” for the second, and “generally impossible” for the third. More precisely, rational equations usually have infinitely many solutions and there is an easy formula which gives them all. Whereas elliptic equations can have finitely or infinitely many solutions, and there is a beautiful theory describing the structure of the solutions and a conjectural way to predict their existence, namely the Birch–Swinnerton-Dyer conjecture. That the equations of general type have at most finitely many solutions was conjectured by Mordell in 1917 and proved by Gerd Faltings in 1984, but there is in general no algorithmic way to find them. The Fermat equation for n>3 is of this type, but here thanks to Wiles we know that there are no rational solutions.

To illustrate why the rational curves, given by second degree equations are easy, consider the Pythagorean equation a^2+b^2=c^2. Dividing by c^2 gives the equation x^2+y^2 =1, where x=a/c and y=b/c, which are rational numbers. We know that this equation describes the set of points (x,y) lying on the unit circle in the xy-plane, with centre (0,0). So we have the equivalent problem of finding the points with rational coordinates on the circle. This translation between algebraic and geometric problems, which was unknown to Diophantus, was discovered by Descartes and eventually developed into the field known as algebraic geometry. In this case the the Diophantine problem, i.e., the problem of finding Pythagorean triples (triples of integers a, b, c with a^2+b^2=c^2), is quite easy and its solution was known already in ancient Greece and even in Babylonian times.

In a certain sense, elliptic curves have the most interesting structure. Giving an effective criterion which allows one to decide whether a given elliptic diophantine problem has a solution, is what the Birch–Swinnerton-Dyer conjecture is about. It is still not proved in all cases, but the formula that Gross and I found gives a solution for a very important special class.

Moving on to talk about some of your own students—Maxim Kontsevich, from the former USSR, arrived in Bonn in 1990 and in 8 years went on to win the Fields Medal. You were his PhD thesis advisor. What was the experience of nurturing a talent like Kontsevich?

DZ: I got to know Russia well because I went there many times and gave many lectures there, and also learned to speak some Russian. But I didn’t meet Maxim while I was there. Somebody else had recommended him and he visited Bonn as an advanced undergraduate for a couple of months and then went back.

Then he asked if he could come again. The problem was that he didn’t have a PhD. In Russia, there were two levels of PhD. One was called “Doktor”, but it didn’t correspond to a European doctorate; it was much higher, and corresponded to what was then the Habilitation in Germany. (The French now also have this, but that is much more recent.) What we would call the PhD was called “Kandidat” there, with a thesis and an exam at about the same level as a western PhD. But he didn’t even have that. He had no degree, and so when he arrived in Bonn, Hirzebruch said that we could give him only a small monthly remuneration until he got his doctorate. He also said that Maxim should work with me, and so I acquired this student. He was very young, something like 20 or so, and it was obvious from the first second that he was much more gifted than I would ever be and also already knew more mathematics than I would ever know, and that always remained true. He had a different level of power from essentially any other mathematician I’ve ever met, and he was already an amazing person even at that age. So I certainly didn’t do much nurturing; if anything, he taught me more things than I ever taught him, and the time that he spent under my “supervision” was also very short, maybe something like four months until he solved the problem that got him not only his PhD, but also the Fields Medal. But nevertheless I did have some contribution.

The story is as follows. The Arbeits-tagung was a fantastic series of annual conferences that started in 1957, and still goes on today, though it has slowed down in the last few years after the passing away of Hirzebruch. The novel feature that made these conferences so special was that the lectures were not programmed in advance but were chosen by the audience one or two days before they were given, with the exception of the opening lecture, which for obvious reasons had to be prepared beforehand and which was always given by Michael Atiyah, always with essentially the same title: “On the Index Theorem and its consequences”, but with totally different content every year. Atiyah was not only one of the greatest mathematicians of the 20th century but also a fabulous lecturer, very exciting and very charismatic.

On this occasion, Atiyah was there, and Maxim was also there. I am nearsighted and sat in the front. Atiyah presented a conjecture of Edward Witten on the intersection numbers in the moduli space of curves, and it was absolutely new. At the end, I called Maxim and said, “Come down. Let me introduce you to Sir Michael Atiyah.” I went to Sir Michael and said, “Let me introduce you to my young student Maxim Kontsevich. He’s the person who will solve the problem you just showed us.” Atiyah looked at me like he had never heard anybody say something so stupid in his life. I can even tell you the day of the week. It was a Friday, because the Arbeitstagung always started on Friday with one lecture in the evening by Atiyah, and with the program discussion to fix the lectures for Saturday and Sunday. And we always had lectures on both of those days, because the auditoriums of the university were free, and had a boat trip on the Rhine on Monday. Typically, everybody came on the boat, some of them to look at the beautiful scenery, but many always busy doing maths. On this occasion, Atiyah and Kontsevich sat at a table discussing mathematics during the whole three hours upstream and the whole two hours back. (It’s faster when you come back downstream.) In those five hours, Kontsevich explained to Atiyah the idea of his proof. So, between Friday and Monday, Maxim had found the proof! And Atiyah was bowled over, and had to concede that my prediction had not been so wild after all. It was clear that he thought that Kontsevich was not an ordinary mortal in mathematics, he was something else. Maxim wrote out all of the details completely in the following two months, but he essentially had the complete proof at the Arbeitstagung. He wrote it up and his thesis is about 23 pages; usually a thesis would be around 150 pages or so, but this is just 23, and the same article, with essentially no change, was submitted to a journal and subsequently got the Fields Medal. So the idea of my having “nurtured” him is, to me, a kind of a joke, but I did introduce him to Atiyah, and I did suggest that he it would be he who would prove Witten’s conjecture.

Another student of yours, Sander Zwegers, has further explored mock theta functions in his dissertation. We would like to hear your reflections on this work. What do you think Ramanujan may really have had in his mind?

DZ: The mock theta functions were introduced, with a list of 17 examples but without any definition, in the famous last letter that Ramanujan wrote to Hardy in 1920 just a few months before his death. Of course we cannot know what Ramanujan had in mind or how he discovered this class of functions; he realised that they were somehow similar to classical modular forms (for which he used the terminology “theta functions”, which is why he called these new and somehow similar objects “mock theta functions”), but he certainly did not know their actual nearly-modular transformation property. This was an open question for over 80 years until Zwegers solved it in his thesis in 2002. He was my student and I had suggested that he look at Ramanujan’s mock theta functions, because they are beautiful q-series and Sander was very good with q-series, but I certainly never expected that he would discover a general theory and find the definition that had been missing for such a long time. I gave a talk on this work in the Séminaire Bourbaki, and there I gave the name of mock modular forms, and the terminology of the “shadow”, but the whole thing was completely due to Zwegers in his thesis and was a brilliant breakthrough.

What excites me in particular is this. Classical modular forms, and also Jacobi forms (whose theory was developed many years ago by Martin Eichler and myself), already played a big role in string theory. But in a paper of Atish Dabolkar, Sameer Murthy and myself it was shown that the mock modular forms also enter mathematical physics and in particular give a description of the string theory of black holes. We posted this work as a long paper on the arXiv in 2012, and since then it has turned slowly into a book which is now nearly finished and is slated to be published by Cambridge University Press in their Cambridge Monographs on Mathematical Physics series.

Can you say a little bit more about Ramanujan’s original mock theta functions, and about Zwegers’ contribution?

DZ: The story is told in detail in my talk “Ramanujan to Hardy: from the first to the last letter”. In it I tell about Ramanujan’s famous last letter to Hardy, in which he gave 17 examples of something that he called “mock theta functions,” but basically just said “I’ve discovered a very interesting class of functions” without giving any actual definition. He said that they had some properties like ordinary modular forms, in particular certain asymptotic properties, but that they were definitely not modular. As I already mentioned, when Ramanujan said “theta functions”, he meant what we now call modular forms, and that is why he called these new objects “mock theta functions”. But he couldn’t pin down their precise transformation property; that is what Sander did in his thesis.

Roughly speaking, a mock modular form, just like a modular form, is a q-series, so it has coefficients that are typically integers having some interesting combinatorial or arithmetic properties just as modular forms do, but it does not have the correct symmetries to make it an actual modular form. Instead, it has what I named a “shadow” (the name is mine, but it’s Zwegers who discovered the concept) which is an ordinary modular form. More precisely, modular forms have an invariant called the “weight”, as I have already mentioned several times, and mock modular forms also have such a “weight”, and if the weight is k then the shadow is an ordinary modular form of complementary weight 2-k. The key property is that if this shadow is 0 then the original function is an ordinary modular form, but if it has a non-zero shadow then it’s mock, so the shadow is the obstruction for a mock modular form to be a modular form.

This means, in particular, that for the 17 functions that Ramanujan had you can write down the list of the 17 corresponding shadows, which will then be actual theta functions, but this is not in Ramanujan’s letter, and I have no idea whether he was aware of them. All of the 17 shadows of his examples were known theta functions, and certainly Ramanujan knew them, and my personal theory, which of course nobody can ever check, is that Ramanujan somehow had that list, and that he realized that each of his functions was associated in some way to a much simpler true theta function. But I don’t know if that is true. All he says in his letter is that he has discovered some functions which have wonderful properties, and that they satisfy beautiful identities.

The description of mock modular forms via their shadows shows that they satisfy the same “magical principle” as ordinary modular forms do: if you know the “fingerprint” (the weight, the level, and a sufficiently large but still finite number of the coefficients of the q-series), then this determines the mock modular form uniquely. Therefore if you have two mock modular forms that you think are equal, you only have to check a finite amount of data in order to prove this, and that means that mock modular forms are potentially just as good for applications in number theory or combinatorics as classical modular forms are.

You have talked about the fascinating world of dilogarithms on many occasions. What are they and what aspects of dilogarithms appeal to you?

DZ: The usual logarithm has a functional equation that everyone knows from high school: \log{ab}=\log{a}+\log{b}. What this means mathematically is that the log function relates the multiplicative group of the non-zero numbers to the additive group of all numbers. On the other hand, in terms of the Taylor series expansion, the logarithm function around 1 can be defined by -\log(1-z)=\sum_{n=1}^{\infty}\frac{z^n}{n} for \vert z\vert<1. The dilogarithm function, denoted \text{Li}_2(z), is defined analogously by the power series \sum_{n=1}^{\infty}\frac{z^n}{n^2} for \vert z\vert< 1, and one can clearly also extend this to the notion of polylogarithm defined by \sum_{n=1}^{\infty}\frac{z^n}{n^m}.

The key property is that the dilogarithm satisfies a certain functional equation, which is a five-term functional equation. This is connected with the sequences of real numbers we discussed earlier, with a certain property that makes them of period five. I mentioned then that if you have a sequence of numbers such that if you add one to any of them the result equals the product of its two neighbours, then the sequence automatically repeats after every five terms, or has period five. This gives the five-term functional equation of the dilogarithm: if you take the five numbers appearing in such a periodic sequence, then the sum of their dilogarithms is not exactly zero, but is something very elementary. This is also connected with a very deep theory called algebraic K-theory: the ordinary logarithm describes the “multiplicative group”, which is a very trivial case of that theory called K_1, but the dilogarithm helps you to understand K_3, which is much deeper, in a similar way. The two problems that I showed to the students in Lyon, leading to periods of length five and length nine, look very similar superficially, but one is just an olympiad-type problem while the other is connected to many deep things including algebraic K-theory, hyperbolic geometry, Schrödinger equation, and many more. In fact, I always had the dream that someday there should be an international conference on the five-term equation where one would bring together people who had encountered these 5-cycles in very different fields and from completely different viewpoints. Then maybe when they talk to each other, we’ll see that these are not just coincidences but that there are some actual connections.

Making a good conjecture is just as satisfying as proving a good theorem

So to answer your question as to what aspects of dilogarithm appeal to me, it is that it connects several things because of the amazing structure encoded in its 5-term functional equation. Historically, I think the first person to discover this was somebody called Spence, but since he isn’t famous enough it’s usually attributed to Abel, and it was rediscovered many times subsequently, by Lobachevsky and others. So this functional equation, although it’s quite a deep property, was not fated to remain undiscovered: if one person didn’t find it, the next person eventually would.

Now back to my personal life. I was in Russia in 1987 to give lectures and work with various people. I spent some two months in Moscow on this occasion, and met many famous mathematicians. It was a very exciting time, including three talks that I gave at the famous seminar of Israel M. Gelfand. It was during this time that I elaborated a conjecture about higher polylogarithms that would relate them to higher algebraic \hbox{K-theory} in the same way as the dilogarithm is related to K_3.

I did calculations on a very primitive computer that I had. I could do very little to substantiate a very nebulous idea that I had originally formulated in my paper on “The remarkable dilogarithm” in the Ramanujan centennial conference at TIFR. At the very end of that paper I mentioned that there seems to be a similar story for the trilogarithm. I had only a couple of numerical examples then, but in Moscow I found many more, also for higher logarithms, and finally formulated a conjecture relating the mth polylogarithm to the higher K-group K_{2m-1}, with an application to special values of Dedekind’s zeta functions as its most important corollary. This is now called Zagier’s conjecture.

I could settle easily the case m=2, based on what was known about the dilogarithm. The case m=3, which is incomparably harder, was proved about four years later in a brilliant piece of work by Alexander Goncharov, whom I also met in Moscow and who became a close friend, while the case m=4 was (almost completely) solved only about three years ago, so after a gap of another 20 years, again by Goncharov and his postdoc Daniil Rudenko. I also had a very good thesis student, Danylo Radchenko, who worked on this in his thesis and who also co-authored several papers with Maryna Viazovska, including one of the two for which she got the Fields Medal two years ago. They were both my PhD students, both came at about the same time, both were Ukrainian, and were both super brilliant. In any case, the conjecture is still only completely solved in a handful of cases, but at least now we have many more ideas than we had a few years ago and my guess today is that in the next 10 years or so, maybe it can be proved for at least m equal to five or six. But in any case it’s a deep conjecture, and I would place it and the work with Benedict Gross on the same par as maybe the two most exciting discoveries of my mathematical life, even though one is a theorem and the other “only” a conjecture.

In mathematics, proving often means that you prove a theorem that somebody else had discovered but that you found a proof of; but to me, discovering a new fact is even more exciting. In my work with Gross, it was he who discovered the thing that should be true. We worked together to find the proof, but the Birch–Swinnerton-Dyer conjecture had been known for a long time, and the idea for how to attack it was found by Gross. But the case of the polylogarithm conjecture was completely different: I didn’t prove anything, but instead found a connection that nobody else had found. And indeed, when I showed it to several people, even while I was still in Moscow, they explained to me that I was too naive and that it was very unlikely that my conjecture was true, because they knew much more about polylogarithms and higher K-theory than I did and therefore knew about possible pitfalls that I was blissfully unaware of. After it was proven for m=3, and after a huge amount of numerical confirmation was found (by me and by other people) for higher values of m, the evidence for the truth of the conjecture became overwhelming, but proving it is a different story. The work with Gross was a theorem that we gave a proof of, and of course I’m proud of it, but I’m equally attached to the polylogarithm story, even though it is still not proved even now. Making a good conjecture is just as satisfying as proving a good theorem, and can be equally difficult.

Maryna Viazovska, one of the four Fields Medallists of 2022, also earned her PhD under your guidance. Working in the seemingly unrelated subject of high-dimensional sphere packings, it was her facility with modular forms that allowed her to construct a key function necessary to prove optimal packing, in both 8 and 24 dimensions. Do you see any promising avenues of research opening up?

DZ: Though it seems an unrelated subject, it isn’t really: the people who work on sphere packing problems have been using modular forms for decades. So the new aspect of her work was not that she used modular forms, but that she used them in a novel way that allowed her to construct the key function needed. She gave a new method for problems of this type and it has led to many new papers. But I’m not sure if one can speak of it as opening up a whole field for sphere packing and optimal designs.

I resolved that mystery in about 10 seconds in my head

By the way, Maryna had written another paper together with Radchenko and another Ukrainian mathematician called Andrii Bondarenko, about a related topic called “spherical t-designs”, while both she and Danylo were still graduate students. They told me that they had done this work, which had nothing to do with the subject of either of their theses and which I didn’t even know about, and had submitted it to the Annals of Mathematics. I was initially sceptical because they were still so junior and presumably didn’t know how hard it is to get a paper published there. But in fact their work had solved a major conjecture, even though two of them were still graduate students, it was indeed accepted, and there was a whole conference about it in Oberwolfach soon afterwards.

Sitting here at ICTP, it sounds topical to talk to you about a paper you jointly authored with Atish Dabholkar, the present director of ICTP, and Sameer Murthy, way back in 2012, which investigated a link between mock modular forms and degeneracies of quantum black holes. We would like to hear your thoughts on this connection.

DZ: Well this work with Atish and Sameer has turned into a book now. How it came about, I can tell you very briefly. I had been invited to a conference in Paris which had such a wonderful title that I couldn’t resist and immediately accepted the invitation, because it contained both the words “black holes”, which everybody has heard of but which I knew nothing about, and “modular forms”, which I love. I was asked to give a survey talk about modular forms, because it was already known that these had some connection to the quantum theory of black holes. While I was there, I attended a beautiful lecture by the famous Indian mathematical physicist Ashoke Sen, in which he spoke of a puzzle to do with counting of certain black hole states, what are called BPS (Bogomol’ny–Prasad–Sommerfield) states and also something to do with Siegel modular forms, but there was a mystery connected with something called “wall crossing”. I resolved that mystery in about 10 seconds in my head, because almost exactly the same thing had appeared in the thesis of Sander Zwegers and he had shown how it related to the mock modular forms that he had just discovered. So after the lecture I went up to the speaker and I said that I knew where the answer to the question he had raised should come from, namely the then brand-new theory of mock modular forms, which of course the physicists had not yet heard of. I told Sen, whom I had just met, that it was obvious to me that Zwegers’ functions were exactly what were needed, although I couldn’t see the details yet, and suggested to him that we might work on it together and maybe write a small paper to check if it’s true. He told me that this would be impossible because he was leaving Paris, but that he had a co-worker there, a string theorist and general relativist who knew black holes well, and that maybe the two of us could work on it. That was Atish Dabolkar. Sen introduced me to Atish, and he and I spent the evening discussing.

The next day, we decided we would work together and Atish asked me if a third person, a young postdoc Sameer Murthy, could also join. So that’s how this came about at this amazing conference with the amazing title. As so often occurs in mathematics, many of the most interesting things happen by chance and through personal contacts.

We only have a couple of questions left. Apart from significant mathematical works, Hirzebruch also built institutions and championed the careers of many deserving mathematicians. What combination of factors do you attribute to the success of these institutions?

DZ: I already mentioned the famous Arbeitstagung (literally, “work meeting”), as one of Hirzebruch’s most original and lasting contributions of inventions. The first Arbeitstagung took place in 1957 from Saturday, July 13, until the following Saturday, and had only six participants, but they were among the most powerful mathematicians of the time—Michael Atiyah, Hans Grauert, Alexander Grothendieck, Friedrich Hirzebruch, Nicolaas Kuiper, and Jacques Tits—and in the following years it grew and became one of the main mathematical events internationally.

Secondly, during his second stay in Princeton in 1955, Hirzebruch was convinced that the model of the IAS—a non-university institution that had few permanent members, but invited both recognized and promising young mathematicians for reasonable lengths of time, in a relaxed atmosphere and free of academic duties and worries—was a wonderful way to promote mathematical research. His goal from then on was to set up an institute of similar type in Germany. After the first abortive attempts to found a Max Planck Institute of Mathematics (MPIM), his long-term vision and persistent efforts for nearly three decades finally bore fruit with the formal setting up of the MPIM in Bonn in 1982. The awareness that the impetus for the creation of the IAS had been the exodus of both Jewish and non-Jewish scientists from Germany in the ‘30s, and the conviction that Germany had a debt to repay, certainly also contributed to his determination.

In your tribute to Hirzebruch, you touch upon his historic address to the Israeli “Knesset”, when he travelled to Israel in May 1988 to receive the Wolf Prize. So this awareness that you mention appears to be always on his mind.

DZ: Hirzebruch was always acutely aware of the German crimes under the Nazi regime. One of the rare occasions when these feelings were made explicit was his acceptance speech of the Wolf Prize in 1988. I was present on that occasion and will never forget the emotions that I felt myself, and also saw running in the audience, on hearing the final words of his speech:

Hirzebruch had an intense relationship with Israel. He first visited the country in 1981, and starting in the late 1980’s became actively involved in the organization of mathematical research there.

Moving to the last one, I was really moved by a sentence that you made in your interview to Mariana Cook, I quote: “When you find a result, it’s not really yours, because it was already true, but you express your personality by the choices you made in discovering and proving it.”

DZ: Yes, it’s my sentence and my belief. Mathematics pursuit is very personal. Even though the discoveries are not really ours—they’re already there!—you still have to choose what you’re going to be interested in, and that choice is very personal.

Often the same theorem is found at roughly the same time by several different people; it was somehow clear that it was the next theorem in that field, and in such a case many people will find it. But sometimes you find something that corresponds very closely to your own way of seeing things and that maybe nobody else would have thought of doing for 20 or even 100 years, because the question itself was not an obvious one to ask.

Another point is the thing that came out today as to which set of people you bring together, like me putting Maxim Kontsevich in touch with the project of Atiyah, or the conference in Paris leading to the discovery of the connection between black holes and mock modular forms. So, just by sheer chance, some mathematics gets done through the interactions of several people: not just personal but even interpersonal.

Also, an idea may be discovered but in a completely different form, like the ancient Indian discovery that gave the name of your magazine Bhāvanā. This was rediscovered by Euler later, but in such a different form that unless you knew, you wouldn’t even see that it’s the same thing. The very same discovery can appear in very different ways, reflecting both the personality of the person who found it and the culture in which it was done.

Thank you so much. These sessions with you were an absolutely fascinating journey into several realms of human endeavours. Quite a unique one. Thanks again for taking us through it.\blacksquare

Footnotes

1. https://link.springer.com/article/10.1007/s40687-018-0175-8 ↩
2. Automorphic Forms, Representation Theory and Arithmetic, Papers presented at the Bombay Colloquium 1979, Published for the Tata Institute of Fundamental Research, Bombay, Springer Verlag, Berlin-Heidelberg-New York, 1981. ↩
3. The second of these papers contains a proof of the so-called “Hilbert-Polya conjecture”; namely, it constructs an operator whose eigenvalues include the products \rho(1-\rho) for all non-trivial zeroes \rho of the Riemann-zeta function. In particular, if this operator is positive definite and self adjoint with respect to some Hilbert space structure on the space on which it acts, then the Riemann Hypothesis would follow. But of course no one has been able to do that. ↩
4. David Zagier has recorded some of his childhood and later experiences in his evocative memoir Botchki: When Doomsday Was Still Tomorrow, originally published in Great Britain in 2000 by Peter Halban Publishers Ltd. ↩
5. Mathematicians – An Outer View of the Inner World, by Mariana Cook, reprinted with corrections by the American Mathematical Society, 2018. A collection of ninety-two photographic portraits, featuring a selection of the most impressive mathematicians of our time, accompanied by autobiographical texts written by each mathematician. ↩
6. See our earlier interview of Sir Michael Atiyah https://bhavana.org.in/sir-michael-atiyah/, Bhāvanā 1(3), 5–18, (2017), on why he returned. ↩
7. During the interview D.Z. mentioned that he discovered long ago that the American spelling for the word “organized” that we adopt, is an anagram of “Don Zagier”, which of course doesn’t work with the British spelling “organised”. ↩
8. Life and Work of Friedrich Hirzebruch, Jahresbericht der DMV 117 (2015), pp. 93–132 ↩
9. Zagier was nominated by the University but the appointment was not allowed by the Ministry of Education because he was three years younger than the official norm of the German state. In fact, he never became a German professor!. ↩
10. This is recorded, for instance, on page 243 of the book Carl Friederich Gauss: Titan of Science by G. Waldo Dunnington, with additional material by Jeremy Gray and Fritz-Egbert Dohse, reprinted in 2004 by the Mathematical Association of America (Incorporated). ↩
11. See page 82 of William Rowan Hamilton, by Edmund Whittaker, Scientific American, Vol. 190, No. 5 (May 1954), pp. 82-87. ↩