
In the previous five parts of the series, we have highlighted examples of geometric constructions in Vedic and Sūtra Literature, the decimal system, topics from ancient Indian arithmetic, and the kuṭṭaka algorithm for expressing the GCD of two numbers as a linear combination of the numbers. We have observed that the invention of most of these methods involve strong algebraic acumen and insights, although they occur well before the conscious emergence of the subject of Algebra as a formal discipline.
This brings us to the question: when does `Algebra’ emerge in India as a distinct discipline and which aspects of this branch of mathematics does one see in ancient Indian texts? The discussions in this part of the series will try to address this question on the basis of extant ancient Indian texts.
On a remark of David Mumford
During a discussion on the history of mathematics over email ten years ago, Fields Medalist David Mumford wrote to the present author (7 February 2013):
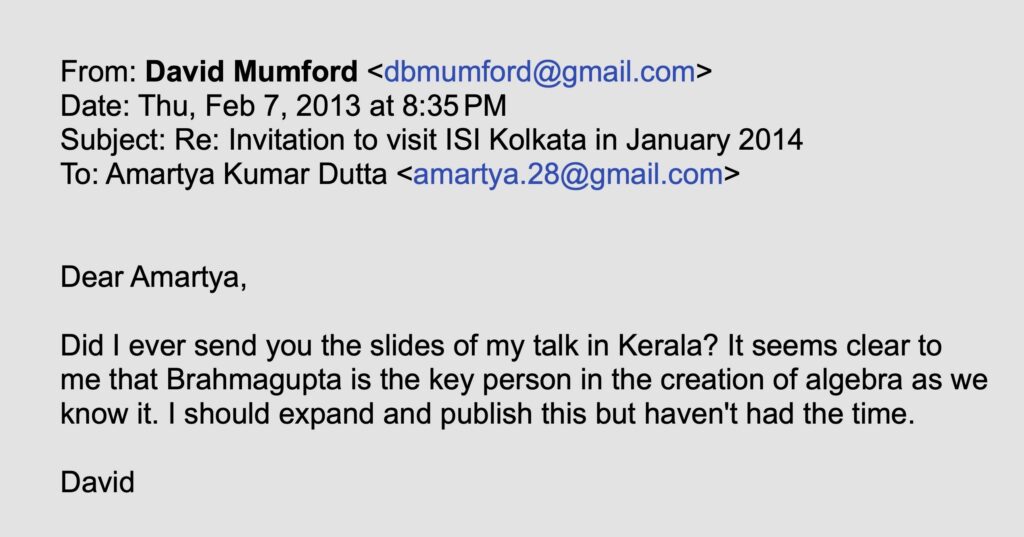
This part of the series will primarily be an exposition of Mumford’s succinct remark.
Now, what is Algebra, more precisely, the “algebra as we know it”? A very interesting description is given by the eminent mathematician Shreeram S. Abhyankar in his unique direct style (see [4], p. 29):
Perhaps the best formal formulation of the phrase “algebra as we know it”, which perfectly matches the lively remark of Abhyankar, can be found in the preface of the treatise [9] on the history of Indian algebra by B. Datta and A.N. Singh. Here, the authors give a precise criterion for identifying the foundations of the science of algebra and explain why Indians may be regarded as the founders of this branch of mathematics:
To see the remarks of Mumford and Datta-Singh in proper perspective, we first classify the algebraic aspects of Indian mathematics into three broad categories:
- Proto-Algebra
- Classical Algebra
- Proto-Modern Abstract Algebra
Proto-Algebra
By Proto-Algebra, we refer to results from antiquity which are algebraic in spirit or substance, but not in form. This includes the “Geometric Algebra” in the Śulba-sūtras (c. 800–500 BCE), discussed in Part 1 of this article (see [9], pp. 27–29). The geometric constructions in the Śulba-sūtras involve applications of algebraic identities such as
(a \pm b)^2=a^2+b^2 \pm 2ab; a^2-b^2=(a+b)(a-b);ab=\Big(\frac{a+b}{2}\Big)^2-\Big(\frac{a-b}{2}\Big)^2;na^2=\Big(\frac{n+1}{2}\Big)^2a^2-\Big(\frac{n-1}{2}\Big)^2a^2;1+3+5+\cdots+(2n-1)=n^2;in fact, the constructions yield geometric representations of the algebraic formulae. Thus, there was awareness of such algebraic formulae, at least in geometric form.
Under Proto-Algebra, we also consider the decimal nomenclature and the decimal notation, and the several computational algorithms that we have seen in the preceding parts of this series, which are rich in algebraic ideas (as discussed earlier), but which are not presented in the language of algebra.
Classical Algebra
`Classical Algebra’ is what Abhyankar refers to lucidly as “High-School Algebra”, i.e., that aspect of algebra whose beginnings are introduced to students in high school under the name `Algebra’; what Mumford refers to informally as “algebra as we know it”. A brilliant efflorescence of `Classical Algebra’ can be seen in India during what is known as the `Classical Age’ of its history. We shall highlight the following foundational aspects of Classical Algebra that can be seen in ancient Indian treatises:
- Creation of the language of algebra:
- Use of distinct symbols for unknowns.
- Extension of the number system (beyond natural numbers).
- Formation of equations.
- Pursuit of the main goal of algebra: solutions of equations.
- Promotion of algebra consciousness and culture.
Besides, we shall briefly indicate the impact of algebra on, and the algebraization of, other branches of mathematics.
Proto-Modern Abstract Algebra
What is now known as `Abstract Algebra’—what Abhyankar refers to as “College Algebra”—emerged and evolved during the nineteenth and twentieth centuries with a revolutionary impact in the mathematical thought process of the modern era.
Now, just as we see the manifestation of algebraic principles in the geometry and computational mathematics of the Vedic, the Sūtra and later periods, for more than a millennium before the emergence of formal Classical Algebra, we see the formulation and the study of composition laws in India in the spirit of Abstract Algebra but in the language of Classical Algebra, more than a millennium before the emergence of modern Abstract Algebra. We shall elaborate on it later.
Unless otherwise stated, the term `Algebra’ refers to `Classical Algebra’.
Brahmagupta as the creator of algebra: An overview
Brahmagupta (born 598 CE) lays a firm foundation on all aspects of basic Classical Algebra listed above in his chapter on algebra titled Kuṭṭakādhyāyaḥ, Chapter 18 of his magnum opus Brāhma-Sphuṭa-Siddhānta (628 CE). In addition, one also sees in this chapter a proto Abstract Algebra in his formulation and study of composition laws. We shall henceforth use the abbreviation BSS for the treatise Brāhma-Sphuṭa-Siddhānta. The original Sanskrit text of BSS is given in [23]; an English translation of Chapter 18 of BSS appears in [6].
We list below the foundational features in the Kuṭṭakā-dhyāyaḥ of Brahmagupta:
- Introduction of symbols for different unknowns.
- Introduction of zero as an integer and the ring-theoretic rules on numbers positive, negative and zero.
- Formation of equations.
- Introduction of the algebra of polynomials.
- Explicit statement of the general formula for roots of arbitrary quadratic equations.
- Introduction of the Gaussian method of elimination for linear equations.
- Announcement of algebra as a distinct important discipline.
The above list indicates why Mumford identifies Brahmagupta as the “key person in the creation of algebra as we know it.”
Note that the above list comprises only those ideas in the Kuṭṭakādhyāyaḥ which we now perceive as being foundational or basic in algebra. This chapter also contains other major topics in algebra. A special mention has to be made of his comprehensive treatment of the kuṭṭakā algorithm for finding integer (rather positive integer) solutions to linear equations of the form ay-bx=\pm c, where a,b,c are positive integers, and his investigations into the problem of finding integer solutions to equations of the form Dx^2+m=y^2, where D is a non-square non-zero integer and m a non-zero integer. Especially remarkable is Brahmagupta’s manifestation of the principle of composition in mathematics—the quintessence of modern abstract algebra—through his composition law `bhāvanā’ on the solution space of Dx^2+m=y^2. Indeed, the name Bhāvanā of this mathematics magazine is inspired by this profound contribution. The `bhāvanā’ law has been discussed in the inaugural issue [10], and a part of the discussion occurs on the inside front cover page of this (and every) issue.
In the rest of the article, we will briefly mention Brahmagupta’s contributions in each of the foundational items, along with some of the relevant preceding ideas in the air around his time. In certain cases, we will also mention elaborations of Brahmaguptas’s ideas by later algebraists.
Pre-Algebra methods for solving problems on linear equations
For a proper historical perspective on the contributions of Brahmagupta (628 CE) to the foundations of algebra, one could contrast the deep work by Indian algebraists from the seventh century with the fact that, prior to the sixteenth century, Arab and European mathematicians have difficulty in addressing mathematical questions which we will now identify as trivial problems on simple linear equations in one variable of the form ax+b=c (a,b,c >0). Therefore, before discussing the Indian foundational works on algebraic symbols and equations, we first explain the pre-algebra regula falsi, or rule of false position, for solving such simple problems. The rule remains very popular in mathematical texts in Europe in the sixteenth century. Even as late as 1542 CE, Robert Recorde2 thinks highly of this rule.
The rule of false position
As the name suggests, it is a `guess and check’, i.e., a `trial and error’ technique using a guess, i.e., a test value (hence the term `false’) for the unknown and then adjusting the test value according to the outcome. Let us first illustrate the rule with an example.
Consider the following problem: 170 apples are distributed equally in 8 closed boxes and two are in excess. How many apples are there in each box?
In the rule of false position, the first step is to guess the number of apples in each box. Say, we guess the number to be 20.
The second step in this rule is to compute the total number of apples (in all eight boxes along with those in excess) that one would have had if the guessed value were correct. Here, the total number with the guessed value 20 would be 20 \times 8 +2=162.
The third step is to compute the error in the computed value of the total (on the basis of the guess) by comparing it with the known value. Here, the error is 170-162=8, and the estimate falls short of the correct total.
Finally, the rule prescribes that when there is an underestimate in the guess, the error is to be divided by the number of boxes and the quotient is to be added to the guessed value to obtain the correct value of the number of apples in each box. Here, the correct answer will therefore be 20+(8\div 8)=21.
The rule of false position may be summarised in our current algebraic language as follows: to solve a problem involving a simple linear equation of the type
ax+b=cin one unknown x, one assumes an arbitrary value, say u, for the unknown x, computes
d=au+b,and then applies the rule
x=u+\frac{c-d}{a} \quad {\rm or } \quad x=u-\frac{d-c}{a},depending on whether c>d or d>c.
The rule of double false position
Another pre-algebraic approach to solving such problems involving (in our language) a simple linear equation of the type ax+b=c is the rule of double false position. The rule is to be explained verbally without the language of algebra. However, for convenience, we cut the story short by summarising the rule using our present algebraic notation.
In this rule, one guesses two values u,v for x, computes the totals
p:=au+b, q:=av+band then determines the errors
e_u:=c-p, e_v:=c-q.
Then the required value is given by
Remark 1.
The rule of false position for solving practical problems on simple linear equations may appear clumsy and weird now. But the applications of this rule take place in a mathematical atmosphere where the following tools are yet to emerge or become standard:
- Symbols, or at least terms, for the unknowns.
- The technique of framing and processing of equations, in some form.
- Negative numbers.
These pillars of Classical Algebra are developed and formalised in ancient India by the time of Brahmagupta (628 CE). Once the concepts get standardised, the solution of a problem on simple linear equations (like ax+b=c) becomes very easy.
Remark 2.
In Indian mathematics, the rule of false position appears in the Bakhshali treatise (probably around 300 CE);3 the initial guess u is called yadṛcchā. The rule disappears in later algebraic treatises beginning with that of Āryabhaṭa (499 CE). However, very limited applications of the rule are found in some of the arithmetical treatises of Śrīdhara (750 CE), Mahāvīra (850 CE) and Bhāskara II (1150 CE). As algebraic notation or terminology is not to be used in such purely arithmetical treatises, the authors have to apply the rule of false position.
Though Āryabhaṭa does not mention the use of algebraic symbols, he uses a term for the unknown: gulikā (shot). He states, in words, a problem of the type
\[\begin{equation}\label{x}
ax+b=cx+d
\end{equation}\]as follows:
Two persons are equally rich. Of them, one possesses a gulikā and b rūpaka (coins); the other possesses c gulikā and d rūpaka; d>b. What is the value of one gulikā in terms of rūpaka? In our algebra notation, what is the value of x in Equation (\ref{x})?
Āryabhaṭa straightaway expresses the following answer, in words, in verse 30 of the chapter Gaṇita (mathematics) in his treatise Āryabhaṭīya (see [24], pp. 72–73):
x=\frac{d-b}{a-c}.
Remark 3.
Even though, on the surface, the rule of false position appears to indicate a lack of algebraic maturity, we point out that there is a certain mathematical sophistication in it. To see this, let
f(x)= ax+b-c,and let \alpha be the root of f(x). Then both the rule of false position and the rule of double false position take the form
\alpha=u-\frac{f(u)}{f^{\prime}(u)},which is the well-known Newton–Raphson formula in Numerical Analysis.
Thus, although the rule of false position is not really needed in solving linear equations, it contains the seeds of the standard method for iteratively finding good approximate roots of real-valued differentiable functions.
Symbols for unknowns
The subject of algebra is commonly associated with the use of letters of the alphabet like x,y,z to denote unknowns. This use of symbols to denote unknowns is indeed one of the two cornerstones of algebra “as we know it”. The systematic use of letters of the alphabet in mathematical presentation has been a great step forward for the rapid progress of the subject.
The use of symbols in Pre-Algebra
Several centuries before the emergence of formal (i.e., symbolic) algebra in Indian mathematics, one comes across striking instances of judicious uses of symbols in major streams of ancient Indian scholarship. The Sanskrit alphabet is based on the phonetic principle of “one sound one symbol”; the decimal notation is based on the principle of “one digit one symbol”. Pāṇini (c. 500 BCE) invents a notation, using letters of the alphabet as symbols, to express rules of grammar. The use of symbols can also be seen in the prosody text of Piṅgala (c. 300 BCE).
In the Bakhshali treatise (c. 300 CE), one sees symbols for the fundamental arithmetic operations. Most or all of these symbols arise as abbreviations—as the first letters of the respective Sanskrit words for the operations. Addition (yuta) is denoted by `yu’; multiplication (guṇa) by `gu’ and division (bhāga) by `bhā’.
Subtraction is denoted by the symbol +, which is probably a simplification of the first letter `kṣa’ of a Sanskrit word kṣaya for subtraction. In later texts, the symbol for subtraction is a dot (occasionally a small circle) above the quantity which is to be subtracted; like \dot{7} denotes -7.

One of the ancient Indian terms for `root’ is mūla which has several meanings in ancient Sanskrit including `root (of a plant)’, `basis’, `cause’, `origin’, etc; thus varga-mūla (square-root) would literally mean `the cause or the origin of the square’. The use of the word mūla for the mathematical concept of `root’ gets subsequently emulated in Arabic and Latin through the corresponding words jidhr (the root of a plant) and radix (root, as in radish or radical) respectively. In the Bakhshali treatise, the symbol for square root is `mū’, the first letter of mūla.
Another Sanskrit word for `root’ is karaṇī; its first letter `ka’ is used in other texts as the symbol for the square root. For instance, in the Bījagaṇita of Bhāskara II,
ka ~ 9 ~~~~ ka ~ 450 ~~~~ ka ~ 75 ~~~~ ka ~ 54means
\sqrt{9}+\sqrt{450} + \sqrt{75}+ \sqrt{54}.At the end of Part 3 of this series ([14], pp. 65–66), we have seen a striking use of symbols in Āryabhaṭa’s ingenious scheme of representing large numbers in astronomy with very few letters of the phonetic Sanskrit alphabet. This must have given a big push to the Indian mathematical mind towards the first step in the invention of `Algebra’—the idea of using letters of the alphabet to denote different unknowns.
Terms for the unknowns
In the Jaina treatise Sthānāṅga-sūtra (c. 300 BCE), there is a term for any unknown quantity: yāvat-tāvat. The word literally means `as many as’, or `so much as’, that is, an arbitrary quantity. Its genesis is obscure, but is probably related to the rule of false position; for its literal meaning is the same as that of the term yadṛcchā in the Bakhshali treatise for the initial guess to be made in this rule.
After the establishment of the science of algebra in Indian mathematics, the word yāvat-tāvat would become the term for the unknown in the study of equations in one unknown, and as the first unknown in the study of equations in several unknowns.
The celebrated Sanskrit lexicographer Amarasiṁha (c. 400 CE) gives the synonym of yāvat-tāvat as māna (measure or quantity). Thus, in the context of algebra, yāvat-tāvat literally means avyakta māna, the measure or value of the unknown.
In the Bakhshali treatise, the zero-symbol is usually used for the unknown, probably to indicate the absence of a certain number in the problem (i.e, the unknown number). In one instance, when there are five unknowns, abbreviations (usually first letters) of the names of the first five ordinal numbers are used for the five unknowns: `pra’ (from prathama, first), `dvi’ (from dvitīya, second), `tṛ’ (from tṛtīya, third), `ca’ (from caturtha, fourth) and `paṁ’ (from pañcama, fifth).
We already mentioned that Āryabhaṭa (499 CE) uses the term gulikā for the unknown. Brahmagupta (628 CE) uses suggestive terms for the unknown, like avyakta (unmanifested) and iṣta (that which is being sought).
Creation of algebra: Symbols for the unknowns
The use of symbols, including letters of the Sanskrit alphabet, in various branches of knowledge including arithmetic, together with the coining of terms for the unknown quantities in mathematical problems, provide a conducive environment for the emergence of the idea of using letters of the Sanskrit alphabet to denote unknowns, the first step in the “creation of algebra as we know it”.
Brahmagupta (628 CE) tersely prescribes the use of varṇa (which means `a colour’ as well as `a letter of the alphabet’) for different unknowns. His commentator Pṛthūdakasvāmin (c. 860 CE) and other subsequent algebraists elaborate. While the first unknown is named by the existing ancient term yāvat-tāvat and symbolically represented by its first letter yā, other unknowns are to be named by distinct colours (varṇa) like kālaka (black), nīlaka (blue), pītaka (yellow), harītaka (green), lohitaka (red) and so on. These unknowns are symbolically represented by the first letter of the names of the respective colours—kā, nī, pī, ha, lo, etc.
Algebraic formalism achieves full development in classical India from the time of Brahmagupta. In the Greek texts of Diophantus, there is a prominent use of a symbol for unknowns; but, unlike in ancient Indian algebra texts from Brahmagupta onwards, there is a single symbol for different unknowns.
As some of the original quotations of famous results from ancient Indian mathematics are in Sanskrit verses, there is often a mistaken notion that ancient Indians do not use symbols and equations.
One must remember that there is a near-universal tradition to describe mathematics in words without symbols, as far as possible, in important documents. Even today, when mathematical accomplishments are recorded in the `Annual Reports’ of research institutes in India, the statements are described in words; symbols are avoided as far as possible.
Even after symbolic algebra gets firmly established in Europe, how does Fermat pose the problem of finding infinite integer solutions of the equation Dx^2+1=y^2, where D is a non-square positive integer? He does so in words! In English translation:
“Given any number whatever, which is not a square, there are also given an infinite number of squares such that, if the square is multiplied into the given number and unity is added to the product, the result is a square.” (cf. Box 5 in [10], p. 18)

Fermat’s statement of his famous “Last Theorem” in the margin of a book is also expressed only in words. It is reproduced in the title page of Andrew Wiles’ famous 1994 paper.
In Indian tradition, the early masters record the essence of their results briefly in verses; details are transmitted orally and sometimes recorded in the commentaries. Brahmagupta verbally describes the use of symbols and equations. However, as per the norms of the time, his treatise is written in brief verses, and hence one does not actually see him using algebraic notation. The notation occurs in Pṛthūdaka’s commentary on his work and in the works of the later masters like Bhāskara II.
Beyond positive numbers: negative numbers, zero, surds, infinity
Number system: positive, negative, zero
One of the striking features of Brahmagupta’s chapter on algebra is the section on positives, negatives, zero and operations thereof (Chapter 18 of BSS, verses 30–35). He clearly states all the rules of fundamental arithmetic operations involving natural (or positive) numbers, negative numbers and zero, treating all three on the same footing. This includes rules like 0 \times a=0, a+(-b)=a-b and the subtler rules involving multiplication of negatives like (-a)b= -(ab), (-a)(-b)=ab, etc. This enlargement of the number system to include zero and negative numbers, imparting to them the status of integers, is a momentous step in the development of mathematics in general, and algebra in particular. To paraphrase in the modern language of abstract algebra, Brahmagupta’s rules give the integers a ring structure, with zero as the additive identity.
In the subsection `The algebraic role of zero’ in Part 3 of this series (see [14], pp. 56–57), we have emphasized the significance of the profound step Brahmagupta takes in elevating zero from a mere place-holder to an algebraic number and stating rules of operations with zero. Below we say a few words regarding Brahmagupta’s role in ensuring that negative numbers have a strong presence in Indian mathematics. Negative numbers are inconspicuous, and probably absent, in the treatise of his great predecessor Āryabhaṭa.
Thanks to treatises like the Arthaśāstra, there has been a strong tradition of accountancy in ancient India (cf. [15], p. 44). Brahmagupta utilizes this to bring out the difference between positive and negative numbers by attaching to them the ideas of `possession’ (dhana) and `debt’ (ṛna) respectively. The precise genesis of negative numbers in India is obscure, but it is from Brahmagupta onwards that the principles and rules of operations involving negative numbers and zero are spelt out clearly to become a part of basic mathematics, or at least basic algebra.
Thanks to the early recognition of negative numbers, Indians could give a unified treatment of the various forms of quadratic equations (with positive coefficients), i.e.,
ax^2+bx=c,~ax^2+c=bx,~ bx+c=ax^2.These cases are treated separately in Arabic texts, and that tradition continued in Europe for a long time.
The acceptance of negative numbers began in Europe only in the sixteenth century. Although Newton strongly advocated negative numbers in the seventeenth century, and gave the rules described by Brahmagupta a millennium back before him, many English mathematicians had difficulty in accepting negative numbers even as late as the eighteenth century. More details on this history are given in Mumford’s paper [18].
Let us recall the words of Felix Klein regarding the subtlety in the concept of negative numbers (see [17], pp. 23–24).
Surds
We quote one identity of Brahmagupta below to illustrate the facility Indian mathematicians display in operating with surds (BSS Chapter 18, verse 40). The rule is often convenient for computing the square root of a binomial surd.
\[
\sqrt{a \pm \sqrt{b}}=\sqrt{\frac{a+\sqrt{a^2-b}}{2}} \pm
\sqrt{\frac{a-\sqrt{a^2-b}}{2}}
\]
Infinity
Mathematicians like Brahmagupta and Bhāskara II (1150 CE) take the bold step of considering numbers with zero in the denominator (calling them kha-cheda and khahara respectively). They are often criticized for this. But, viewed with an open mind, one can see that they simply follow a different convention from ours and there is nothing mathematically unsound in their approach; in fact some of their approaches have analogues in modern higher mathematics. The theme will be discussed in a subsequent part of the series. These numbers give rise to an algebraic concept of infinity and they are likely to have inspired calculus-type concepts among Indian mathematicians.
Bhāskarācārya (Bhāskara II) defines rules of interactions of such an algebraic infinity \infty with finite numbers:
\infty +x=\infty; ~~ \infty -x=\infty,as also some other enigmatic rules to be discussed in a subsequent part. We quote below his celebrated simile to explain the results \infty \pm x=\infty.
bahuṣvapi syāllayasṛṣṭikāle’nante’cyute bhūtagaṇeṣu yadvat
The idea of adjunction of infinity has been put on a firm footing in several branches of higher mathematics like analysis or valuation theory in commutative algebra and number theory. We shall discuss these in a subsequent part.
Creation of algebra: Equations
Formation of equations
Let us again recall the statement of Datta–Singh (see [9], p. vi) quoted earlier:
We have seen that Indian mathematicians in the Classical Age make systematic use of the letters of the alphabet to denote unknowns. They also introduce the concept of `equation’ and make clear, detailed and organised presentations regarding the procedures for forming and processing equations.
The term for an equation, or more precisely, the work of forming an equation, is called samī-karaṇa (also samī-kāra or samī-kriyā). The Sanskrit word sama means `equal’; the word karaṇa means `operation’ in mathematics (from kṛ meaning `to do’). Thus the Sanskrit word samīkaraṇa, which literally means `making equal’ or `equating’, is a fitting term for an `equation’.
The book of Datta–Singh (see [9], pp. 28–36) gives details about the Indian methods for forming equations, plan of writing equations (called nyāsa, literally, writing down, putting down; i.e., plan of the layout), preparation (or processing) of equations (called samaśodhana, or śodhana, i.e., equi-clearance or complete clearance) and classification of equations. While equations are called samī-karaṇa and unknowns as yāvat-tāvat (the first unknown) or colour-names (for other unknowns), the coefficients of unknowns are called guṇaka (or guṇakāra), the known (visible) portion of the equation (what we call the `constant coefficient’ or `constant’) as rūpa; for instance, in 2x+1, 2 is the guṇaka and 1 is the rūpa. The suffix for `to the power’ is gata for powers above four; for second, third and fourth powers, the terms are varga, ghana, varga-varga respectively.
An equation in mathematics is a statement of equality between two algebraic expressions. In our modern presentation of an equation, the two expressions are connected by an equality sign =, one expression being to the left and the other to the right of the equality symbol. The style of Indian algebraists is slightly different. In the Brahmagupta-Pṛthūdaka tradition of writing an equation in one unknown, the terms of similar denominations are written one below the other. Such an arrangement does not require any sign for equality. For instance, the equation 10x-8=x^2 + 1 is represented as
| yā va | 0 | yā | 10 | rū | \dot{8} |
| yā va | 1 | yā | 0 | rū | 1 |
If there are several unknowns, those of the same kind are written in the same column. Like the equation 197x-1644y-z=6302, i.e., 197x-1644y-z+0=0x+0y+0z+6302, is represented as
| yā | 197 | kā | 164\dot4 | nī | \dot1 | rū | 0 |
| yā | 0 | kā | 0 | nī | 0 | rū | 6302 |
One can see that such tabular arrangements are convenient for processing equations. This is yet another instance of the algorithmic approach of Indian algebraists—the equations are presented in an algorithmic style. Further details are given in [9].
The algebra of polynomials
The algebra of polynomials in several unknowns, i.e., the rules for addition, subtraction and multiplication of polynomials, is described by Brahmagupta (BSS, Chapter 18, verses 41–42):
tulyānāṁ saṁkalitavyavakalite pṛthagatulyānām
anyo’nyavarṇaghāto bhāvitakaḥ pūrvavaccheṣam
Quadratic equations in one unknown
Method of completing the square: A revisit
The formula for the roots of the quadratic equation
\[\begin{equation}\label{quadratic}
ax^2+bx=c; a \ne 0,
\end{equation}\]where a,b,c are known quantities, as also the well-known algorithm for solving the equation by the method of “eliminating the middle term” or “completing the square” are explicitly stated in post-Vedic ancient Indian mathematics texts. Let us analyse the method.
The underlying strategy is to transform the equation (\ref{quadratic}) to the form y^2=d, where d is a known quantity. This is achieved by “eliminating the middle term” (i.e., bx).
The latter is achieved by the idea of “completing the square”: multiplying the equation (\ref{quadratic}) by 4a to get
4a^2x^2+4abx =4ac,i.e.,
(2ax+b)^2=4ac+b^2Setting y:=2ax+b, we see that the above equation takes the desired form
y^2=d,where d:=4ac+b^2 is a known quantity since a,b,c are known. Since y can now be determined from d, the problem of solving the quadratic equation (\ref{quadratic}) reduces to solving the linear equation 2ax+b=y, where a,b,y are known; and the solution is straightforward.
Combining all the above steps, one thus obtains the formulae for the roots of the quadratic equation (\ref{quadratic}) as:
\[\begin{equation}\label{formula}
\dfrac{\pm \sqrt{4ac+b^2}-b}{2a}
\end{equation}\]
Problems on quadratic equations in the Bakhshali treatise and Āryabhaṭīya
The author of the Bakhshali treatise (c. 300 CE) and Āryabhaṭa (499 CE) are clearly aware of formula (\ref{formula}) though they do not state it for arbitrary coefficients.
As we have seen in [15], p. 43, Āryabhaṭa has given the formula for finding the number of terms n of an A.P. series, whose first term a, common difference d and the sum S are all known, as
\[\begin{equation}\label{AP}
n=\frac{1}{2}\Big[\frac{\sqrt{8dS+(2a-d)^2}-2a}{d}+1\Big].
\end{equation}\]The expression for n arises as a root of the quadratic equation
dx^2+ (2a-d)x =2S. The formula (\ref{AP}) also appears in the Bakhshali treatise.
Moreover, as we have mentioned in Part 4 of this series (see [15], p. 45), Āryabhaṭa has also given the solution to a problem on Interest I (when the Principal P, Time T and Amount A are known) as
I=\frac{\sqrt{APT+(\frac{P}{2})^2} - \frac{P}{2}}{T};this I arises as a root of the quadratic equation
Tx^2+Px=AP.The Bakhshali treatise considers problems of the following type (see [9], pp. 60–61):
In our notation, let x denote the number of days that elapses before the first person overtakes the second. Since the second person had already travelled for t days, the total distance covered by him when he gets overtaken by the first person is then c(t+x) yojana.
From the information on the first person, the total distance in yojana covered by him during the x days, that is, before overtaking the second person, is
a+ (a+b)+ (a+2b)+ \cdots + (a+(x-1)b)=ax+\frac{bx(x-1)}{2}.Equating, we have
bx^2-(2(c-a)+b)x =2tc,whence
x= \dfrac{\sqrt{(2(c-a)+b)^2+8btc}+2(c-a)+b}{2b}.(Note: here, x cannot be negative.)
This formula for the number of days is correctly stated in words in the Bakhshali treatise.
Theory on quadratic equations by Brahmagupta–Śrīdhara–Bhāskara II
In BSS Chapter 18 verse 44, the formula (\ref{formula}) is stated explicitly by Brahmagupta (628 CE) for arbitrary coefficients, and he is the earliest known author to do so:
mūlam madhyenonaṁ vargadviguṇoddhṛtaṁ madhyaḥ
For the convenience of the readers, we insert symbols, as in (\ref{quadratic}), in brackets, in the translation below:
Brahmagupta names the topic “Quadratic Equations” as madhya-haraṇa (“elimination of the middle”), which gives a hint regarding the method adopted to arrive at the formula (\ref{formula}) for the roots – the method of elimination of the middle by completing the square, explained above.
Śrīdharācārya (750 CE) explicitly describes this method ([9], p. 65), which is hinted at by Brahmagupta through his terminology madhya-haraṇa. Hence the method of “completing the square” is now popularly known as Śrīdharācārya’s method.
Bhāskara II (1150 CE) makes a lucid exposition of the method of completing the square in his treatises Līlāvatī and Bījagaṇita. The version in the Bījagaṇita, which Abhyankar was fond of quoting, is given below ([1], p. 33–34 ;[19], p. 120):
avyaktasya varga rūpairyukto pakṣau tato mūlaṁ
A numerical example of Bhāskara II
Numerous concrete problems have been formulated by Indian mathematicians to illustrate the theory of quadratic equations. We quote an illustrative example composed by Bhāskara II which occurs in both Līlāvatī (see [21], pp. 127–128; [20], pp. 74–75) and Bījagaṇita (see [1], p. 34 ; [19], p. 120–121):
nikhilanavamabhāgāścālinī bhṛṅgamekam
niśi parimalalubdhaṁ padmamadhye niruddhaṁ
pratiraṇati raṇataṁ brūhi kānte’lisaṅkhyām
Through such lyrically presented problems, the poet-mathematician is also training the reader to develop an innovative skill in applying the theory of quadratic equations. In the above problem, since the total number of bees is sought, it will be natural to denote this unknown number by y (say) and obtain the equation
y-\sqrt{\frac{y}{2}} - \Big(\frac{8}{9}\Big)y=2.Bhāskara advises ([21], pp. 127–128) considering the number sought to be 2x^2; i.e., he implicitly recommends the substitution x= \sqrt{\frac{y}{2}} in the above equation to obtain the neater equation
2x^2-x-\Big(\frac{8}{9}\Big)(2x^2)=2.Now one has
\frac{x^2}{9}-\frac{x}{2}=1.By the method of completing the square, and obviously considering only the positive solution, one obtains the value of the intermediary: x=6; and thus deduces the number of bees in the cluster to be 2x^2=72.
Reduction to linear and quadratic equations
Ancient Indian texts do not contain any method for solving arbitrary cubic and biquadratic (degree four) equations in one variable. However, Bhāskara II shows ([9], pp. 76–77) how to make innovative use of the completing the square (or cube) technique to reduce such higher degree equations to linear or quadratic equations in certain specific numerical examples. For instance, he considers the equation
x^3+12x=6x^2+35,i.e.,
x^3-6x^2+12x=35.In this case, one can `complete the cube’ on the LHS by adding -8 on both sides to obtain
(x-2)^3=3^3which reduces to an easy linear equation. Another example of Bhāskara II is the equation
x^4-2x^2-400x=9999.With some algebraic ingenuity, one can prepare the ground for an application of the completing the square method. Adding 4x^2+400x+1 on both sides, one obtains
(x^2+1)^2=(2x+100)^2from which one obtains a quadratic equation
x^2+1=2x+100.After a method for solving the general cubic equation is discovered by the Italian mathematicians del Ferro, Tartaglia and Cardano during the first half of the sixteenth century, Ferrari discovers a method for solving the general biquadratic equation by reducing it to the cubic case. It can be seen that the ideas involved in Bhāskara II’s solution to the equation x^4-2x^2-400x=9999 are precisely the ideas involved in Ferrari’s method, the tool of completing the square playing a major role.
Mahāvīra (850) considers (see [9], pp. 79–81) problems involving equations of the type
\[\begin{align*}&a_1\sqrt{b_1x}+a_2\sqrt{b_2\Big(x-a_1\sqrt{b_1x}\Big)}\\
&\qquad+a_3 \sqrt{b_3\Big\{(x-a_1\sqrt{b_1x})-a_2\sqrt{b_2(x-a_1\sqrt{b_1x})}\Big\}}\\
&\qquad+ \cdots +r=x.\end{align*}\]It may look horrible at first sight, but by a suitable sequence of substitutions, the problem reduces to solving a sequence of quadratic equations of the form
x-a\sqrt{bx}=r.For instance, a concrete problem posed by Mahāvīra leads to the equation
\[\begin{align*}&4\sqrt{\frac{x}{2}}+8\sqrt{\frac{1}{10}\Big(x-4\sqrt{\frac{x}{2}}\Big)}\\
&\qquad+9 \sqrt{\frac{1}{2}\Big\{\Big(x-4\sqrt{\frac{x}{2}}\Big)-8\sqrt{\frac{1}{10}\Big(x-4\sqrt{\frac{x}{2}}\Big)\Big\}}}\\
&\qquad+ 56=x.\end{align*}\]One makes the sequence of substitutions
y=x-4\sqrt{\frac{x}{2}}and
z=y-8\sqrt{\frac{y}{10}}.The given equation reduces to the quadratic equation
z-9\sqrt{\frac{z}{2}}=56.Solving it, one obtains z=128 and thus a quadratic equation
y-8\sqrt{\frac{y}{10}}=128.Solving it, one obtains y=160 and thus a quadratic equation
x-4\sqrt{\frac{x}{2}}=160.Finally, one obtains the solution x=200.
One is reminded of the kuṭṭaka algorithm discussed in Part 5 (see [16]). In fact, the above methods of Mahāvīra and Bhāskara II illustrate the `divide and conquer’ strategy or the reduction principle that one sees prominently in the kuṭṭaka algorithm.
Abhyankar on the madhya-haraṇa or “completing the square” idea
The Brahmagupta-Śrīdhara madhya-haraṇa method by “completing the square” is an idea with far-reaching consequences in mathematics.
For
x^2+bx+c,the Brahmagupta-Śrīdhara substitution
y=x+\frac{b}{2}eliminates the middle term. Extending this idea, one can easily see that for the general polynomial
x^n+b_1x^{n-1}+\cdots +b_n,the substitution
y=x+\frac{b_1}{n}kills (i.e., eliminates) the coefficient b_1. This generalisation is known as the Tschirnhausen transformation (1683). In his famous historical article [3] (for which Abhyankar was awarded the Chauvenet Prize of the Mathematical Association of America in 1978), Abhyankar emphasises the importance of this elimination trick by pointing out its pivotal role in the resolution of singularities, one of the major landmarks in algebraic geometry in the twentieth century4 (see [2], p. 417):
Again, Abhyankar highlights the important influence of Śrīdharācārya’s “completing the square” idea in his own proof of a certain theorem of Newton (see [4], p. 74):
Simultaneous equations in several unknowns
Gaussian method of elimination
In BSS Chapter 18 verse 51, Brahmagupta describes the “method of elimination” for solving simultaneous linear equations. His rule applies to both indeterminate as well as determinate systems of equations. The method is now commonly known as Gaussian elimination.
Simultaneous quadratic equations
The solutions to several problems involving simultaneous quadratic equations have been described by Indian algebraists. We give a few examples below:
\[\begin{align*}
&x-y=d,\qquad \;\;\; \!xy =b;\\
&x+y=a, \qquad \;\;\; \!xy=b;\\
&x^2+y^2=c,\qquad xy=b;\\
&x^2+y^2=c, \qquad x+y=a;\\
&x^2+y^2=c,\qquad x-y=d;\\
&x^2-y^2=m, \qquad \!\!\! xy=b.\end{align*}\]Precise details and further examples are given in ([9], pp. 81–87).
Indeterminate equations
From at least the time of Āryabhaṭa, ancient Indians make systematic investigations of the hard and subtle number-theoretic problem of finding integer solutions of various equations, especially equations of the first and the second degree. In Part 5, we have discussed in detail the kuṭṭaka algorithm for finding integers satisfying linear indeterminate equations of the form ax-by=c, where a,b,c are integers. In a subsequent part, we plan to discuss the Indian cakravāla algorithm for solving quadratic indeterminate equations of the form Dx^2+1=y^2, where D is a positive integer which is not a perfect square. Some discussions on the problem have already been made in [10].
Influence of algebra in other branches of Indian mathematics
Arithmetic, combinatorics and geometry
In Part 3 (see [14]), we have seen that algebraic thinking pervades all algorithms for the fundamental operations in Indian arithmetic. Moreover, some of the methods are indeed statements of algebraic identities in words. For instance, we have seen ([14], p. 62) that to compute the square of a number n, Brahmagupta recommends a judicious use of the algebra identity
n^2=(n-a)(n+a)+a^2;and Śrīdhara mentions the algebra identity
n^2=1+3+5+\cdots+(2n-1).We have also seen ([14], p. 62) with numerical examples that Brahmagupta describes in words the algebra identity \frac{a}{b}=\frac{a}{b+h}+\frac{a}{b+h} \times \frac{h}{b} for readily obtaining, in certain special cases, the quotient and remainder of a division.
In Part 4 (see [15], pp. 43–44), we have seen the algebra formulae for various progressions (A.P., G.P. and various summation formulae). We have discussed in ([11], p. 35) the influence of Algebra in the early emergence of the concept of Weighted Arithmetic Mean in various avatars. The strong algebra culture also results in a strong combinatorics culture in ancient India. We have discussed a few early combinatorial results in Part 2 (see [13]); we hope to have further discussions in a future part. We also plan to mention, in a future part, Brahmagupta’s constructions of triangles and cyclic quadrilaterals whose sides and areas are rational numbers.
Trigonometry, calculus and analysis
In a future part, when we discuss trigonometry in ancient India, we shall see that Indian mathematicians impart an algebraic character to trigonometry. Indeed ancient Indian trigonometry resembles its modern algebraic form. Apart from inventing the sine and cosine functions, Indians discover important trigonometric formulae and identities, including basic composition formulae like
\sin (A \pm B) =\sin A \cos B \pm \cos A \sin B,which too were named bhāvanā (composition).
A landmark result in Indian mathematics is the following second-order interpolation formula of Brahmagupta presented in Khaṇḍakhādyaka (IX, 8) around 665 CE:
\[\begin{align*}f({\theta}_n+x)&=
f({\theta}_n)+\frac{x}{h}\,\frac{{\Delta}_{n-1}+ {\Delta}_n}{2} –
\Big(\frac{x}{h}\Big)^2\, \frac{{\Delta}_{n-1}- {\Delta}_n}{2}\\
&= f({\theta}_n)+\frac{x}{h}\,\frac{{\Delta}_{n-1}+ {\Delta}_n}{2} +
\Big(\frac{x}{h}\Big)^2\, \frac{{{\Delta}^2}_{n-1}}{2}.\end{align*}\]One can see that the above algebraic formula is a special case (i.e., up to second-order difference) of the Newton-Stirling interpolation formula.
The strong foundation in algebra and the prevalence of an enthusiasm for algebra in Indian mathematical culture provide a conducive environment for the emergence of the formulae and algorithms in calculus and analysis in India. This is a vast topic which we hope to elaborate on in a future part.
In praise of algebra
In the hands of Brahmagupta, the subject of algebra emerges in India as a distinct branch of mathematics and becomes one of its central pillars. After evolving through several stages, algebra has now come to play a key role in modern mathematics both as an independent area in its own right as well as an indispensable tool in other fields. In fact, the twentieth century witnessed a vigorous phase of “algebraization of mathematics”. Algebra provides elegance, simplicity, precision, clarity and technical power in the hands of mathematicians.
In this section, we shall present quotes from a few Indian mathematicians, including Brahmagupta, to see how strongly they emphasise the importance of algebra. In retrospect, it is remarkable how early, and accurately, they realise the significance of algebra.
Brahmagupta in praise of algebra
While Āryabhaṭa is the first known savant in ancient India to compose a separate chapter on mathematics in a major astronomy treatise, Brahmagupta (628 CE) is the first known author to compose a separate chapter on algebra in a treatise. The chapter Kuṭṭakādhyāyaḥ begins with a statement regarding the indispensability and the power of the subject, and lists its core topics (BSS XVIII, verses 1–2):
jñātuṁ vakṣyāmi tataḥ kuṭṭākāraṁ saha praśnaiḥ
ācāryastantravidāṁ jñātairvargaprakṛtyā ca
The opening verses of the Kuṭṭakādhyāyaḥ show Brahmagupta as a pioneering visionary who recognises and announces Algebra as a distinct, powerful and indispensable branch of mathematics. He defines the scope of the subject and emphasises its importance.
In the concluding verses of the Kuṭṭakādhyāyaḥ (BSS XVIII, verses 99–100), Brahmagupta reiterates the importance of Algebra and speaks about the delight and glory it brings.
anyairdattān praśnānuktairvā sādhyet karaṇaiḥ
kuṭṭākārapraśnaiḥ paṭhitairapi kiṁ punarjñātaiḥ
There is thus an implicit emphasis on the pursuit of algebra for its intrinsic mathematical importance, for the generation of new research and for its applications. These are precisely some of the modern criteria for outstanding research.
In addition, Brahmagupta asserts that the pursuit of algebra will fetch glory, an assurance which would undoubtedly be an effective motivating incentive for most budding mathematicians! In this context, the present author is reminded of an anecdote which took place in the Guest House of IISc in December 2003, where both he and Abhyankar were staying. Another visitor to IISc, on meeting Abhyankar, struck a conversation with him during which he excitedly asked the maestro about the factor that motivates him to pursue the hard questions in his fields (algebra and algebraic geometry). Prompt came Abhyankar's reply:
Bhāskarācārya in praise of algebra
To emphasise the importance, power and profundity of algebra, the great poet-mathematician Bhāskara II begins his treatise Bījagaṇita (see [1], p 7; [9], II, p 4) with the following invocation:
adhiṣṭhitaṁ satpuruṣeṇa sāṅkhyāḥ
vyaktasya kṛtsnasya tadeka bījaṁ
avyaktamīśaṁ gaṇitaṁ ca vande
In his commentary on Bhāskara's Bījagaṇita titled Bījapallava, the sixteenth century mathematician Kṛṣṇa explains that the Invocation pays homage to:
- The Avyakta (Unmanifested) Prakṛti directed by the Puruṣa, the Self-existent Being, of the Sāṁkhya philosophy.
- The Avyakta (Transcendental) Īśa or God, the Sat-Chit-Ānanda or Brahman of the Vedanta philosophy.
- The Avyakta-gaṇita, literally, computations (mathematics) with unmanifest (i.e., unknown) quantities.
It is a Sanskrit synonym for Bījagaṇita, the science of Algebra. Its antonym Vyakta-gaṇita refers to the mathematics with manifest quantities, such as arithmetic, geometry, etc.
Correspondingly, the word Sāṁkhya has been used with three meanings which are respectively:
- A system of Indian philosophy.
- Those who have realised the Self (or Brahman).
- Those who are proficient in saṁkhyā (numbers), i.e., mathematicians.
The word Buddhi too has been used with the following meanings in the respective contexts:
- Intelligence, Consciousness.
- Tattvajñāna, the True Knowledge of Reality.
- Mathematical knowledge and intellect.
Thus the first verse of Bhāskara's Bījagaṇita may be translated as:
We have seen that algebraic ideas pervade arithmetic and geometry in India from the Vedic period; that there is a dormant algebra in the major concepts, constructions and algorithms of ancient Indian mathematics. This ubiquity of algebra in mathematics (including concrete branches like arithmetic and geometry) is being highlighted here by Bhāskarācārya.
In the epilogue in Bījagaṇita, Bhāskarācārya strongly advocates the study of algebra:
sakala gaṇita sāraṁ sopapatti prakāraṁ
iti bahu guṇa yuktaṁ sarva doṣairvimuktaṁ
paṭha paṭha mati buddhyai labdhidaṁ prauḍha siddhai
Nārāyaṇa in praise of algebra
In the opening verses of both Part 1 and Part 2 of his algebra treatise titled Bījagaṇitāvataṁsa, Nārāyaṇa Paṇḍita makes an Invocation to the Gods as well as to the science of Algebra, in the spirit of the Invocation by Bhāskara II. We quote below the English translations by Datta–Singh of the two verses (see [9], p.5):
In verses 5-6 of Part 1 of the same treatise, Nārāyaṇa also explains (see [9], p.5):
Brahmagupta's announcement of Algebra as a Shastra
Apart from the fact that Brahmagupta has created the central pillars in the language of algebra—symbols for unknowns and the concept of equations—and established all ring-theoretic rules of operations with all integers (including negative numbers and zero), what distinguishes Brahmagupta as “the key person in the creation of algebra as we know it” is the fact that he announces Algebra as a distinct discipline, lists and arranges the topics which belong to it–and his choice of topics matches our notion of Algebra–and strongly advocates the cultivation of this branch of mathematics, as we see in the previous section. One gets reminded of an observation of Sri Aurobindo ([26], p. 67):
The Aṣṭādhyāyī of Pāṇini readily comes to one's mind as an illustrious example of the above observation. What is not sufficiently known is that the Kuṭṭakādhyāyaḥ of Brahmagupta (Chapter 18 of BSS) too fits the above description. Indeed, Brahmagupta observes certain salient features of mathematics, systematizes them and creates the science of algebra.
Algebra occurs in an implicit form in the mathematics of several ancient civilizations. In India, the constructive geometry of the Śulba-Sūtras involves algebraic formulae in geometric form. The discoveries of certain algorithms in computational arithmetic are also indicative of a subtle algebraic acumen. Principles and results, which may be identified as belonging to algebra proper, can be found in texts preceding BSS. Brahmagupta's great predecessor Āryabhaṭa has several algebra-type results and algebraic ideas in his pioneering treatise Āryabhaṭīya: there is a term for an unknown quantity, there are solutions of linear and quadratic equations, there are formulae for arithmetic progression and related sums of finite series and there is a subtle method for solving the linear indeterminate equation ax-by=c in integers. Thus many ingredients of basic algebra are already there, mostly placed in the later half of the mathematics chapter of Āryabhaṭīya. And one may justifiably call Āryabhaṭa as a founder of algebra in India for his algebra-type results.
However, although there are algebraic principles and results in some Indian texts preceding BSS, one is yet to see a conscious formulation of the science of algebra as a Śāstra. That leap is taken by Brahmagupta when he compiles a separate chapter on topics in algebra and emphasises its importance. He is the first known mathematician to compose a separate chapter on algebra in a treatise, or even to define the subject.
Thus, while going through ancient Indian mathematics, one gets the feeling that if there is a moment in Indian history when the creative Word from the god of mathematics took the following form and result: “Let there be Algebra and there was Algebra”, then it must have been the composition of the Brāhma-Sphuṭa-Siddhānta by Brahmagupta (628 CE). This treatise gives a distinct identity to Algebra in the chapter Kuṭṭakādhyāyaḥ.
One may justifiably say that Babylonians were doing algebra, the Vedic Indians, Chinese and Greeks were doing geometric algebra; and so on. But they were perhaps not conscious that they were doing algebra. These early developments are remarkable achievements, but a conscious development of a subject is a contribution at a different level—much more profound in its impact. It is doubtful whether even Diophantus had a clear, well-structured vision of algebra.
Brahmagupta's impact on Indian mathematics can be seen from the fact that for several centuries after BSS appears, many of the stalwarts among Indian mathematicians like Śrīdhara (750 CE), Pṛthūdakasvāmin (c. 860 CE), Padmānabha, Jayadeva, Śrīpati (1039 CE), Bhāskara II (1150 CE) and Nārāyaṇa (c. 1350 CE), to mention a few, consciously focus their energies to the development of algebra.
Brahmagupta appears to name the subject of algebra by kuṭṭaka (pulverisation); the current Sanskrit name bījagaṇita appears later. The term kuṭṭaka, reminiscent of Fermat's “descent”, indicates that it is a process of solving mathematical problems by a process of simplification—by breaking quantities (for instance, the coefficients or solutions of a given equation) into progressively smaller pieces. It captures a sophisticated aspect of the subject.
Brahmagupta's bhāvanā: A forerunner of modern abstract algebra
During the twilight years of ancient India, Bhāskara II (1150) declares Brahmagupta to be Gaṇaka-Cakra-Cūḍāmaṇi (Crest-Jewel among the Mathematicians).
In our time, during the National Mathematical Day lecture session on Ramanujan on 22 December 2020, Manjul Bhargava mentions Brahmagupta as among the most creative of the world’s mathematicians in whose work there is a magical quality which was inspiring for him; and added that the kind of ideas that are present in Brahmagupta's Brāhma-sphuṭa-siddhānta around 600 CE just “blows your mind”.
What makes Brahmagupta a special name in the galaxy of mathematicians? Many are his feats, but perhaps the most mind-boggling is the fact that he lays the foundations of Classical Algebra, that is, creates the “algebra as we know it”, and also manifests in mathematics the very principle of composition, the quintessence of the modern subject `Abstract Algebra'. The principle of composition pervades the whole of modern algebra and number theory. And, as we explain below, this creator of Classical Algebra introduces, in disguise (that is, in the language of classical algebra), a highly sophisticated level of abstraction.
Recall that Brahmagupta's composition law `bhāvanā' defines a binary operation \odot on the (a priori unknown) roots of the equation Dx^2+z=y^2 (D a positive integer) as follows:
(x_1,y_1, z_1) \odot (x_2,y_2, z_2) = (x_1y_2 + x_2y_1, Dx_1x_2 + y_1y_2, z_1z_2).We have discussed the magnificence and significance of this law in the inaugural issue of this publication Bhāvanā (see [10]).
But now let us have an overview of the pedagogy of Abstract Algebra to have a better understanding as to why the presence of the `bhāvanā' law in an early seventh-century text “blows your mind”.
In the study of Abstract Algebra, a student of mathematics gets introduced, gradually, to three layers of sophistication. At the first level (say, the B.Sc. Mathematics Honours level), the student learns about abstract structures (sets with binary composition laws) like Groups, Rings, Fields and Vector Spaces. In the typical examples of such abstract structures, like the group of permutations on n distinct symbols, the group of invertible n \times n matrices with entries from real numbers, the ring of integers, the polynomial rings, the composition laws occur naturally.
Having mastered this first layer of abstraction, the student of mathematics next learns to associate such abstract structures to mathematical objects. For instance, to each polynomial f(X) is associated a group G(f) known as the Galois group and there are deep theorems on the relationships between the polynomial f(X) and its Galois group G(f) which help deduce certain properties of the polynomial f(X) from the corresponding properties of the group G(f). Again, groups are associated with topological spaces to gain insights on those spaces.
So far, the abstract structures occur naturally. In the third layer of abstraction comes the idea of constructing a suitable composition law on an important set, i.e., to impart an abstract structure on the set, for a deeper study of the set. For instance, mathematicians have discovered that there is an `addition law' (or a `group law') on points of an `elliptic curve' y^2= (x-a)(x-b)(x-c), a, b, c distinct, which makes the curve an abelian group. The discovery of laws like \odot is an important theme in modern mathematical research
However, it is usually at a research level that some students of mathematics come across this third level of abstraction; and that too if they specialise in certain specific directions. Brahmagupta's bhāvanā belongs to this layer: Brahmagupta constructs a law of composition on the solution space of an equation, in order to study the equation! In the early seventh century! While investigating a challenging problem, he bypasses the first two layers of abstraction and straightaway enters the summit!
Possible mystic influences on algebra in India
We have seen that, while introducing infinity in algebra, Bhāskara II uses a mystic metaphor to explain his result \infty \pm x = \infty, drawing a parallel with Lord Viṣṇu who is referred to as Ananta (endless, boundless, eternal, infinite) and Acyuta (firm, solid, imperishable, permanent). Perhaps the spiritual culture had prepared the Indian mind for, and probably suggested to it, the concept of the mathematical infinity (or zero!) with its curious properties.
Indeed, we have seen that Bhāskara II begins his treatise on algebra with a pun involving mystic and algebraic concepts; and Nārāyaṇa emulates him.
One of the terms for the `unknown' (the variable to be solved, what we usually call x) that Brahmagupta uses in stating his composition law is iṣta (that which is sought), a word whose typical use in Indian tradition is in the concept of the iṣta-devatā, the chosen deity whose realisation is the seeker's aim.
The Vedas record mystic experiences in a symbolic language—like Agni (Fire) is the symbol of spiritual aspiration, the Ashwa (Horse) is the symbol of the Life-Force, the Go (Cow) is the symbol of the Light, of Consciousness in the form of knowledge, and so on. The symbols are used to express subtle truths or phenomena that are intangible to the ordinary human mind.
One can see a parallel between the use of symbols in such early spiritual treatises to express that which is unmanifested to the (unrealised) seeker, and the use of symbols in later technical treatises to express that unknown quantity which is being sought. One may then wonder whether the former has played an impalpable role in influencing the latter.
In this context, it may be relevant to note that Sri Aurobindo uses algebraic metaphors while discussing the Veda. He describes the Veda as a book of “esoteric symbols”, of “spiritual formulae”; as a “divine algebra” transmitting “eternal formulae” and that it uses a symbolic language for expressing (through mystic suggestion) that which is inexpressible to the ordinary mind. He writes in “The Secret of the Veda” (see [25], p. 363; p. 11):
Awareness about ancient Indian algebra in modern scholarship
English translations of ancient Indian mathematics texts, especially of Bhāskara II, began appearing from the early nineteenth century. Bhāskara's algebra treatise Bījagaṇita was translated from Persian5 into English by E. Strachey under the title Bija Ganita or the Algebra of the Hindus (London, 1813). The Līlāvatī of Bhāskara was translated from the original Sanskrit by John Taylor (Bombay, 1816).
The work during this period which, perhaps, had the greatest impact in generating awareness about ancient Indian mathematics was the translation [6] by H.T. Colebrooke in 1817 of the texts Līlāvatī and Bījagaṇita of Bhāskara II and the chapters Gaṇitādhyāyaḥ and Kuṭṭakādhyāyaḥ of the Brāhma-Sphuṭa-Siddhānta of Brahmagupta. Colebrooke also wrote a long preface where he discussed some of the distinguishing features of the texts. This preface was reproduced in Colebrooke's Miscellaneous Essays (1837) and its contents thereby got the attention of a wide community of serious scholars on India's cultural history. One of the features of Indian algebra that Colebrooke highlighted in the above book (p. 438):
References to the invention of algebra in India occur in the subsequent writings of various scholars and thinkers in various contexts, at various time points. We quote a few representative examples. The German mathematician H. Hankel asserted in 1874 that Indians were the real inventors of algebra:
In a speech “India's Gift to the World” delivered at the New York City and reported in the Brooklyn Standard Union on 27 February 1895, Swami Vivekananda makes a reference to the invention of algebra in India along with the invention of the decimal system and other branches of mathematics (see [28], pp. 511-512):
In his famous text on History of Mathematics (1919), the American historian of mathematics F. Cajori highlights the Indian genesis of the algebra of modern times along with the Indian genesis of the decimal notation and modern arithmetic (see [5], p 97):
T. Dantzig (1930) too refers to algebra originating in India alongside the decimal place-value system (see [7], p. 19):
In this century, S.S. Abhyankar makes references to the journey of algebra from India to Europe via Arabia, in his inimitable style – drawing a parallel with his own sea-voyage from Bombay! (see [3], pp. 131 and 136)
We have seen that, as in arithmetic, many topics in algebra that one learns up to the high school stage had been systematically developed in India. However, as the word `algebra' has been derived from the Arabic word `al-jabr' of al-Khwārizmī (c. 825 CE), there has been a misconception that the subject algebra itself begins with the Arabs—this is a common misconception even (or especially?) in India!
John Stillwell writes in (see [27], pp. 82–83):
Brahmagupta's work, the high point of Indian mathematics to that time, was more advanced than al-Khwārizmı's in several respects—notation, admission of negative numbers, and the treatment of Diophantine equations—even though it predated al-Khwārizmī and was very likely known to him. Indian mathematics had spread to the Arab world with the general promotion of culture by the eighth-century caliphs of Baghdad, and Arab mathematicians acknowledged the Indian origin of certain ideas, for instance, decimal numerals. Why then did al-Khwārizmī's work rather than Brahmagupta's become the definitive “algebra”?Perhaps this is a case (like “Pell's equation”, to mention another pertinent example) where a mathematical term caught on for accidental reasons. However, it may be that the time was ripe for the idea of algebra to be cultivated, and the simple algebra of al-Khwārizmī served this purpose better than those of his more sophisticated predecessors.
Thus, ironically, it is perhaps the sophistication achieved by ancient Indians in algebra that has hindered the awareness about their achievements and contributions! It is as if, being too ahead of his time, Brahmagupta was over-qualified, and hence disqualified to be acknowledged as a creator of algebra!
Quite often, we see that Indian contributions get altogether omitted even by highly respected historians of mathematics. For instance, the book “The History of Mathematics: A Reader” (1987) by J. Fauvel and J. Gray has no representation of mathematics in India, and the monograph “The Beginnings and Evolution of Algebra” (2000) by I.G. Bashmakova and G.S. Smirnova has no mention of the algebra of post-Vedic ancient India.
Perhaps that increases our responsibility to be adequately informed about what is currently known regarding the development of algebra in India.\blacksquare
References
- [1] S.K. Abhyankar (ed), Bījagaṇita of Bhāskarācārya, Bhaskaracharya Pratishthana (1980).
- [2] S.S. Abhyankar, Historical Ramblings in Algebraic Geometry and Related Algebra, The American Mathematical Monthly, 83(6), 409-448 (1976).
- [3] S.S. Abhyankar, Resolution of Singularities and Modular Galois Theory, Bulletin of the American Mathematical Society, 38(2), 131-169 (2001).
- [4] S.S. Abhyankar, Lectures on Algebra Volume I, World Scientific (2006).
- [5] F. Cajori: History of Mathematics, Macmillan (1919), AMS Chelsea (2000).
- [6] H.T. Colebrooke, Algebra, with Arithmetic and Mensuration, from the Sanscrit of Brahmegupta and Bhascara, John Murray, London (1817); reprinted Cosmo Pub (2004); Sharada (2005).
- [7] T. Dantzig, Number: The Language of Science, Macmillan (1930).
- [8] B. Datta, The Bakhshali Mathematics. Bulletin of the Calcutta Mathematical Society, 21, 1-60 (1929(i)).
- [9] B. Datta \& A.N. Singh, History of Hindu Mathematics Part II, Motilal Banarasidass (1938); reprinted by Asia Publishing House (1962) \& Bharatiya Kala Prakashan (2004).
- [10] A.K. Dutta, The bhāvanā in Mathematics, Bhāvanā 1(1), 13-19 (2017).
- [11] A.K. Dutta, Weighted Arithmetic Mean in Ancient India, Bhāvanā 1(4), 24–36 (2017).
- [12] A.K. Dutta, Mathematics in Ancient India Part 1: Geometry in Vedic and Sūtra Literature, Bhāvanā, 6(1), 23-33 (2022).
- [13] A.K. Dutta, Mathematics in Ancient India Part 2: Computational Mathematics in Vedic and Sūtra Literature, Bhāvanā, 6(2), 43-61 (2022).
- [14] A.K. Dutta, Mathematics in Ancient India Part 3: The Decimal Notation and some Arithmetic Algorithms, Bhāvanā, 6(3), 50-67 (2022).
- [15] A.K. Dutta, Mathematics in Ancient India Part 4: Principles of Arithmetic, Bhāvanā, 6(4), 36-49 (2022).
- [16] A.K. Dutta, Mathematics in Ancient India Part 5: The Kuṭṭaka Algorithm, Bhāvanā, 6(5), 52-67 (2023).
- [17] F. Klein, Elementary Mathematics from an advanced standpoint, MacMillan (1932).
- [18] D. Mumford, What's so Baffling About Negative Numbers? Studies in the History of Indian Mathematics (ed. C.S. Seshadri), Hindustan Book Agency, 113–143 (2010).
- [19] V.B. Panicker (ed), Bhaskaracharya's Bijaganitham, Bharatiya Vidya Bhavan (2006).
- [20] K.S. Patwardhan, S.A. Naimpally, S.L. Singh (eds.), Līlāvatī of Bhāskarācārya. Motilal Banarasidass (2001).
- [21] A. Padmanabha Rao, Bhāskarācārya's Līlāvatī Part I, Chinmaya International Foundation Shodha Sansthan, Ernakulam (2015).
- [22] Svami Satya Prakash Sarasvati and Usha Jyotishmati (eds.), The Bakhshali Manuscript, Dr. Ratna Kumari Svadhyaya Sansthana, Allahabad (1979).
- [23] R.S. Sharma (ed.), Brāhma-Sphuṭa-Siddhānta of Brahmagupta. Indian Institute of Astronomical Research (1966).
- [24] K.S. Shukla and K.V. Sarma (eds.), Āryabhaṭīya of Āryabhaṭa. Indian National Science Academy (1976).
- [25] Sri Aurobindo, The Secret of the Veda, Sri Aurobindo Ashram, Pondicherry (1999).
- [26] Sri Aurobindo, The Foundations of Indian Culture, Sri Aurobindo Ashram, Pondicherry (1989).
- [27] J. Stillwell, Mathematics and Its History, Springer Second Edition, Indian reprint (2013).
- [28] Swami Vivekananda, Complete Works Vol. II (10th edition), Advaita Ashram, Kolkata (2012).
Footnotes
- We mention here that in early Indological discourses, the word “Hindu” was inclusive of Jain and Buddhist, and may be read as a term for all residents of ancient India. ↩
- A brief mention of Robert Recorde is made in Part 4 (see [15], p. 41). ↩
- Historians of mathematics differ in their estimates of the date of this work. The mathematical content of the Bakhshali treatise suggests that it predates the Āryabhaṭīya of Āryabhaṭa (499 CE). B. Datta estimates that the original version of the treatise was composed around the third century CE or earlier. Datta's estimate is in tune with the radiocarbon dating (224–383 CE) of one of the folios at the University of Oxford's Bodleian Libraries. ↩
- H. Hironaka was awarded the Fields Medal in 1970 for solving the problem of resolution of singularities in characteristic zero; Abhyankar made important contributions on the problem in positive characteristic. ↩
- Based on the Persian translation of 1634 CE by Ata Alla Rushdi. ↩
- The word “Brahmin” was often used by early western writers to refer to scholars in ancient India. ↩
