
The year 2021 marks the bicentennial birth anniversary of Pafnuty Chebyshev, considered to be one of the founding fathers of Russian mathematics.
Introduction
In 2021, we celebrate the 200th anniversary of the birth of Pafnuty Lvovich Chebyshev, a major 19th-century mathematician who contributed to a variety of fields including number theory, probability, the integration of algebraic functions, approximation theory, the theory of orthogonal polynomials, cartography, the theory of mechanisms, ballistics and several other topics in pure and applied mathematics.
Chebyshev emphasised the importance of mathematics in the applied sciences, and conversely, he was convinced of the fact that the development of theoretical research in mathematics should always be motivated by practical problems. He is considered as the founder of the first Russian Mathematical School of Saint Petersburg, to which he gave a new direction, after more than a century distinguished by the direct influence of Leonhard Euler and his disciples. In a book published in 1983 [17], P.J. Davis writes that Chebyshev “is one of the patron saints of Russian mathematics, and it is due in no small measure to him that Russian mathematics today stands second to none in the world.”Chebyshev’s impact on mathematics is strongly felt world-wise, not only in Russia.
In the pages that follow, I shall report on Chebyshev’s life and work, mentioning in particular some of his contributions to number theory, approximation theory, probability, geography, the fitting of garments and ballistics. His important work on the theory of mechanical linkages is reviewed in another paper in this issue of Bhāvanā [53]. While our main subject here is Chebyshev’s life and work, we shall try to give a picture of the mathematical atmosphere in which he worked, also mentioning some of his colleagues and students. At several places, we shall also allude to Euler, Chebyshev’s famous predecessor in Saint Petersburg, establishing relations between the works of the two men.
Childhood and education
Pafnuty Lvovich Chebyshev was born on May 16, 1821,1 in a family with nine children, in the village of Okatovo, about 80 km south-west of Moscow, in the district of Borovsk, Kaluga province. The village is situated about 10 km from the science city of Obninsk2 and was part of a larger property of his father, Lev Pavlovich Chebyshev, a retired army officer of noble descent, who had fought Napoleon’s armies trying to invade Russia. Had it not been for a physiological problem that made him limp substantially (he had one leg shorter than the other), it is probable that the young Pafnuty would have embraced a military career, following his father. This was the path taken by his younger brother Vladimir Lvovich who became a general, and was also a professor at the Saint Petersburg Artillery Academy. Pafnuty used to walk with a cane, which kept him, as a child, from taking part in certain games that children of his age used to play; and at one point he was a bit of a lonely child. It is not unreasonable to assume that this loneliness contributed to his tendency for deep thought and invention.

Until the age of 11, the young Pafnuty received all his education at home, primarily from his mother, Agrafena Ivanovna Pozniakova Chebysheva, who taught him reading and writing, and from a cousin, Avdotia Quintilianovna Soukhareva, from whom he learnt French and arithmetic.
One of Chebyshev’s favourite occupations since his early childhood was the construction of mechanical toys using rudimentary instruments like a penknife. He built miniature mills and other refined objects. At the same time, he was capable of making connections between the mechanics of these toys and the geometry lessons he was taking. Chebyshev maintained a lifelong passion for building machines and mechanical devices with his own hands, which eventually led him to the construction of calculating machines, wooden automata that imitated walking humans or horses, and other instruments. Some of these machines are displayed today at the Conservatoire National des Arts et M étiers in Paris, at the Academy of Sciences in Saint Petersburg, at the Museum of History in Moscow, at the museum dedicated to Chebyshev hosted in a school named after him in the village of Mashkovo which is a few kilometers from his birth place, and at other places.

In 1832, the Chebyshevs moved to Moscow so that the young Pafnuty, together with his older brother, could receive adequate training to enter the university there.
In Moscow, Pafnuty continued to be educated at home, where he was tutored in mathematics by P.N. Pogorelski, one of the most renowned teachers of elementary mathematics in Moscow, and also the author of some of the finest high school textbooks in Russia.
Unlike several other Saint Petersburg mathematicians born in the first half of the nineteenth century, Chebyshev did all his studies in Russia.3 In 1837, at age 16, he entered the faculty of physics and mathematics of Moscow University, and here his talents attracted the attention of the mathematician N.D. Brashman,4 who held the Chair of Applied Mechanics. All his life, Chebyshev had a profound respect for Brashman, both as a mathematician and as a person. It is said that Chebyshev asked him for a photograph of his, that he always carried in his wallet; in fact, Chebyshev had it on him even at the moment of his death. Chebyshev obtained his candidate degree5 in the spring of 1841 with a memoir titled On the numerical solution of algebraic equations of higher degree. That year, famine was raging in Russia after serious epidemics had affected large parts of the country in the preceding years. As a consequence, his father’s business collapsed. While his family was not able to help him financially anymore, Chebyshev continued concentrating his efforts on mathematics. B.N. Delone writes in [19][p. 3]: “In order to avoid going hungry, the young Chebyshev, fresh from university studies, was compelled either to serve somewhere or give lessons. Reasoning that such occupations would distract him from mathematics, he chose want.”

In 1843, Chebyshev published a paper in French, in the Journal de math ématiques pures et appliqu ées,6 titled Note on a class of multiple indefinite integrals [12][p. 3-6]. The study of such integrals was a fashionable subject at that time. As a by-product of the result of this short paper, Chebyshev obtained new proofs of formulae that are due to Liouville and Augustin-Louis Cauchy on the multiple integration of some special functions. The paper immediately attracted the attention of the Belgian-French mathematician Eugène Catalan, who was probably informed about it by the editor of the journal, since in the same issue, Catalan too published a 2-page complement to Chebyshev’s results.

In 1844, Chebyshev published a second paper in French, this time in Crelle’s journal, titled Note on the convergence of the Taylor series [12][p. 9-14], in which incidentally he points out a mistake in Cauchy’s famous Exercices d’analyse et de physique math ématique (vol. 1, p. 29), regarding the integration of an infinite series of functions. In his words, Chebyshev proved in that paper a result which “is a very simple consequence of the remarkable discoveries of Mr. Cauchy, but at the same time, it contradicts the convergence rule for series given by this celebrated geometer.”7 Indeed, Cauchy asserted (mistakenly) that the definite integral of some infinite series of functions is (without further conditions) equal to the infinite sum of the integrals of these functions. After quoting Cauchy’s defective rule, Chebyshev wrote: “It seems to me that the deficiency of this rule follows from the fact that Mr. Cauchy supposes that the value of a definite integral can be developed as a convergent series, if the differential between the integration limits can be developed as a convergent series. But this happens only in special cases.”
It is not surprising that after these two papers, Chebyshev, who was then only 23 years old, became well-known among French mathematicians; this was a prelude to friendly relationships that he established with them a few years later, and which lasted until the end of his life.
In the same year, Chebyshev defended a Magister thesis8 at the University of Moscow, under the supervision of Brashman, with the title An essay on an elementary analysis in probability theory [10].
Saint Petersburg and work on number theory
In 1847, after his graduation, Chebyshev realized that it was not possible for him to get a suitable position in Moscow, and he moved to Saint Petersburg where he had a teaching offer. He submitted there a pro venia legend dissertation9 whose title was On integration by means of logarithms.10 [14] This title refers to the problem of expressing indefinite integrals of the form
\[\int\frac{x+A dx}{\sqrt{x^4+ax^3+bx^2+cx+d}}\]
in terms of logarithms of algebraic functions. In its most general form, this is a difficult problem, and it was explicitly posed by Ostrogradsky, who was a professor in Saint Petersburg and who was impressed by the results obtained by the young Chebyshev. The latter had been working on this question since 1843. In the same dissertation, Chebyshev presented the state of the art for the general problem of integrating irrational differentials (in particular square roots of rational functions), mentioning related works of Jacobi, Abel and others.
After he defended this pro venia legendi, Chebyshev obtained a position of Adjunct Professor at the Imperial University of Saint Petersburg, where he started teaching Algebra and Number Theory. It happened that at that time, the Saint Petersburg Academy of Sciences had undertaken the project of publishing an edition of Euler’s works on number theory (99 memoirs in all). The leader of this project, V.Y. Bunyakovsky,11 who noticed Chebyshev’s talent, invited him to contribute to that edition. In 1849, Bunyakovsky and Chebyshev published two large volumes titled Index syst ématique et raisonn é des oeuvres arithm étiques d’Euler which included all of Euler’s previously published papers on the subject together with annotations on several of them, correcting several mistakes in the transcription of Euler’s dictation that were introduced by his young collaborators, and who used to help him in writing his papers. Indeed, though Euler was blind for the last 17 years of his life, his mathematical activity never decreased, and his two children, Johann Albrecht and Christoph, his students, and other mathematicians were helping him in his correspondence. The edition also included unpublished manuscripts from the Academy’s archives.
C.A. Possé, the author of the biography in [12], tells us that there were two mathematicians with whom Chebyshev established a close relationship after his arrival at Saint Petersburg: Bunyakovsky whom we just mentioned, and another eminent mathematician, I.I. Somov,12 who like Chebyshev, studied in Moscow under the guidance of Brashman. Bunyakovsky and Possé were well-known, not only for their scientific achievements, but also for their moral qualities.

It is very probable that Chebyshev, who had been working on probability and analysis, started being interested in number theory by reading Euler’s papers. In fact, we learn from the biography in [12] that Chebyshev was an assiduous reader of works of great mathematicians of the past, including Euler, Joseph Louis Lagrange, Carl Friedrich Gauss and Niels Hendrik Abel, and that in general, he abstained from reading the mathematical works of his own contemporaries, considering that this would distract him from having original ideas.
Chebyshev rapidly concentrated his efforts on the hardest problem in number theory, namely, the distribution of prime numbers. Euler, Chebyshev’s famous predecessor in Saint Petersburg, in his paper titled Discovery of a very extraordinary law of numbers in relation to the sum of their divisors [22], written in 1747, wrote the following about this problem:
Chebyshev introduced completely new ideas in this area, developing methods that stand at the foundation of the field of analytic number theory. His first paper on this subject was presented at the Saint Petersburg Academy of Sciences in 1848, and was published in Liouville’s Journal four years later. It is titled On the function which determines the totality of prime numbers which are smaller than a given limit [12][p. 29-48]. The content of this paper also constituted the third appendix of his doctoral dissertation submitted a year later. The fundamental object of investigation in this paper is the function \varphi(x) which to each positive integer x assigns the number of primes that are \leq x. Chebyshev obtained the first definite result on this function, correcting assertions that were made, based on empirical observations, by Adrien-Marie Legendre before him,13 and making them more precise. Chebyshev proved in particular that one can approximate the function \varphi(x) by the integral \int_2^x\frac{dx}{\log x}.14 He also showed that no matter how small the real a>0 is and no matter how large the integer n is, the difference between \varphi(x) and \int_2^x\frac{dx}{\log x} is less than ax/\log^n x for infinitely many x. Let us read the beginning of his paper:
The theorem to which Chebyshev refers in the above quote asserts that for any integer n, given a positive real number \rho, the infinite sum
\[\sum_{x=2}^{x=\infty}\big( \varphi(x+1)-\varphi(x)-\frac{1}{\log x}\big)\frac{\log^n x}{x^{1+\rho}} \]
converges to a finite limit as \rho approaches zero. In his proof of this theorem, he uses the behaviour of Euler’s real zeta function \zeta(s)=\sum_{n=1}^{\infty} n^{-s} at s=1. It is useful to remember here that Euler had already discovered a fundamental relation between the zeta function and prime numbers, namely,
\[ \zeta(s)=\prod \frac{1}{1-\frac{1}{p}},\]
where the product is taken over all prime numbers p (see [20]).
Among the other results proved in Chebyshev’s paper is the fact that no matter how small we take the value \alpha>0 and no matter how large we take the integer n, there is no value x beyond which the graph of the function \varphi(x) lies completely below the graph of the function
\[\int_2^x \frac{dt}{\log t}-\frac{\alpha x}{\log^n x}\]
or above the graph of the function
\[\int_2^x \frac{dt}{\log t}+\frac{\alpha x}{\log^n x}.\]
Delone considered this result as the first nontrivial theorem on the distribution of primes since the time of Euclid [19][p. 14].
Another fundamental result from the same paper by Chebyshev, in modern formulation, says the following (see [9][p. 79]):
\[ \liminf_{x\to\infty}\frac{\varphi(x)}{x/\log x}\leq 1\leq \limsup_{x\to\infty}\frac{\varphi(x)}{x/\log x}.\]
This implies that if the ratio \frac{\varphi(x)}{x/\log x} has a limit as x\to\infty, then this limit is necessarily 1. Moreover, Chebyshev showed that the same ratio lies between 0.92 and 1.11 for x sufficiently large.
The fact that the limit of \frac{\varphi(x)}{x/\log x} is indeed 1 was obtained independently in 1896 by J. Hadamard and J.-Ch. de La Vall ée Poussin. Both proofs rely on methods of complex analysis (a topic in which Chebyshev was not involved), and they are both based on the fact that Riemann’s (complex) zeta function \zeta(s) has no zero on the line \mathfrak{R}(s)=1. The result proved by Hadamard and de La Vall ée Poussin is known as “The prime number theorem”. It was stated without proof by Gauss in either 1792 or 1793 (when he was barely 15 or so ) and by Legendre in either 1797 or 1798. A more recent proof of this result, which avoids complex analysis, was given in 1949 by P. Erdös and A. Selberg.
In 1849, Chebyshev defended a doctoral thesis on number theory titled The theory of congruences, which was later published as a book. It became a classic, and remained for several decades the only available Russian textbook on number theory. The two reviewers of Chebyshev’s doctoral thesis were Bunyakovsky and P.H. Fuss.16 The dissertation was followed by three specialized appendices, titled On quadratic residues, On the determination of primitive roots, and On the number of primes not exceeding a given number. The book was translated into German in 1888 and into Italian in 1895 [11]. Chebyshev received the Demidov award for this work from the Saint Petersburg Academy of Sciences.
The year after he obtained his doctorate, Chebyshev was elected extraordinary professor of Mathematics at the University of Saint Petersburg. Ten years later, in 1860, he became ordinary professor.17
In 1850, Chebyshev published, again in Liouville’s Journal, another paper on the distribution of primes, titled Memoir on prime numbers [12][p. 51-70]. In the introduction, he recalls that most of the existing statements regarding the distribution of primes were based on the examination of large tables of primes, and remain essentially unproven. He gives as an example the so-called Bertrand Postulatum which asserts that for any a>3, there always exists a prime number between a and 2a-2.18 He then mentions other types of questions, concerning series indexed by primes. He starts by recalling that Euler proved that the series
\[\frac{1}{2^a}+ \frac{1}{3^a}+ \frac{1}{5^a}+\frac{1}{7^a}+\frac{1}{11^a}…,\]
indexed by the primes, and the series
\[\frac{1}{2^a}+ \frac{1}{3^a}+ \frac{1}{4^a}+\frac{1}{5^a}+\frac{1}{6^a}…, \]
indexed by all integers \geq 2, converge or diverge for exactly the same values of a (they both converge if and only if a>1).

He shows that this is not a general rule, proving, as a counter-example, that while the series
\[ \frac{1}{2\log 2}+ \frac{1}{3\log 3}+ \frac{1}{5\log 5}+ \frac{1}{7\log 7}+… \]
indexed by the primes has a limit whose value is <1.73, the series
\[ \frac{1}{2\log 2}+ \frac{1}{3\log 3}+ \frac{1}{4\log 4}+ \frac{1}{5\log 5}+\frac{1}{6\log 6}+…, \]
indexed by all integers \geq 2, is divergent. Motivated by such observations, he addresses the general problem: To find a criterion for the convergence of a series indexed by prime numbers, and in the case where this series converges, to find a good approximation of its sum. He describes a general approach to this problem, which involves considering the function \theta(x) which, for any number x, gives the sum of the logarithms of all primes that are at most x.19 He obtains a remarkable functional equation satisfied by this function, which allows him to give a proof of the Bertrand Postulatum. A shorter proof of this result was given in 1919 by S. Ramanujan [49].
Chebyshev’s name is attached to several other results and conjectures in number theory, and I would like to mention one of them, known under the name Chebyshev’s bias. This is an observation that he made in a letter he sent to P.N. Fuss, published in [12][Vol. I, p. 697-698]. It says that one can see empirically that there are more prime numbers of the form 4k+3 than of the form 4k+1. This observation is considered now as a conjecture, and it is still unproven despite the effort of many prominent mathematicians. We refer the reader to a report on this problem by M. Rubinstein and P. Sarnak [50].
Chebyshev’s results on number theory are reviewed in Delone’s book [19], an exposition which has the advantage of presenting at the same time both Chebyshev’s work, and its impact on that of his students.
Chebyshev’s work on number theory made him a natural candidate for membership at the Saint Petersburg Academy of Sciences. In 1853, he was elected there, but to the chair of applied mathematics, since the three chairs of pure mathematics were occupied by Bunyakovsky, Fuss and Ostrogradsky. In 1859, Chebyshev became an Ordinary Member of the Academy, one year before he became Ordinary Professor at the University.
Journeys to France and contacts with French mathematicians
In the early 1840s, Chebyshev started establishing contacts with the most renowned mathematicians in Western Europe, and in particular, France. Unlike many mathematicians of his epoch, he disliked writing letters and communicating on mathematics by correspondence. He preferred direct communication, and he traveled a lot. His biographers [12], [51] mention that he used to spend almost every summer in Western Europe, and his favourite destination was Paris. His collected works [12] contain a report on a trip to Western Europe he made in the summer of 1852.20 The report is addressed to the emperor Nicholas I, who, as the patron of the Academy of Sciences, funded the stay abroad. The countries visited included France, England, Belgium and Germany, but Chebyshev spent most of his time in France. It is interesting to skim this 12-page report because it tells us how broad Chebyshev’s interests were.
We learn from this report that on his way to Paris, Chebyshev stopped in Lille, a city in Northern France, for the purpose of observing the nearby wind-mills. He comments on the curvature of the surface of the wings of these mills, and he declares that one can easily write an analytical expression for the energy produced by them. He discusses the problem of finding the most advantageous form of these wings, and he notes that wind-mills are the cheapest machines that can be used for grinding grain, making oil, pounding flax, and for other purposes. These observations provide us with an early indication of Chebyshev’s special interest in optimization theory, which he developed later in several papers. Incidentally, it is noteworthy that Euler, who was Chebyshev’s forerunner at the Saint Petersburg Academy, besides being one of the main founders of theoretical mechanics, was also involved in the study of several practical mechanical problems; like Chebyshev, Euler was aware of the connection between mathematics and engineering. Like Chebyshev, Euler worked on the mathematical theory of wind-mills, cf. his memoir titled Refined researches on the effect of wind-mills [27]. Among his other memoirs, we mention the following whose titles are quite explicit: A more complete theory of machines that are put in motion by the reaction of water [25] and On the action of saws [26].

We also learn from Chebyshev’s report that although the universities in Paris were closed for the summer vacation when he arrived there, he managed to meet the mathematicians he was hoping to see, with the aim of collecting information for his studies in applied mechanics. He first met Liouville, who introduced him to several other eminent mathematicians. We note incidentally that Chebyshev was perfectly fluent in French, a fact which was not uncommon among educated Russians of the 19th Century. He went to the Conservatoire des Arts et M étiers in Paris21 and he admired the collection of machines that were displayed in the museum of this institution. He visited several firms near the French capital, being particularly interested in those where steam engines were constructed. He then traveled to other French regions to observe factories, including the Lorraine region for its metallurgical plants and foundries, the city of Lille for its paper mills and Châtellerault for its munition factories. He went to other places where he examined machines used for cotton and flax spinning, systems for raising water, etc. Let us note here that Euler too had comparable interests, see for instance his memoirs A more particular discussion on the various methods with which water is raised using pumps with the greatest effectiveness and Advices for the most advantages arrangement of the machines used in raising water via pumps [23], [24]; there are other papers of Euler on related subjects.
Chebyshev declares in his 1852 report that he was particularly interested in the engines designed by the Scottish engineer James Watt,22 in automata built by the French inventor Jacques de Vaucanson,23 and in the arithmetic machine invented by Blaise Pascal.24 At the same time, Chebyshev had fruitful mathematical discussions with Cauchy, Liouville, Irénée-Jules Bienaymé, Charles Hermite, Joseph Alfred Serret, Henri Lebesgue, Jean-Victor Poncelet and Alphonse de Polignac. The subjects of these conversations included the theory of differential equations and the integration of algebraic differentials, two topics on which he worked in the years that followed. Chebyshev mentions in his report that Liouville and Hermite suggested that he further develops the ideas contained in his pro venia legendi dissertation on the integration of the square roots of rational functions, and indeed this became the subject of several articles he published afterwards.
Before returning to Russia, Chebyshev traveled to England where he visited factories and examined machines constructed by Watt. On Sundays and in the evenings, when the factories were closed, he used his time to discuss with Arthur Cayley, James Joseph Sylvester and other mathematicians. He writes that through Cayley and Sylvester he was introduced to the railway engineer C.H. Gregory. In London, he visited the Royal Polytechnic Institution (which later became the University of Westminster) where he admired a large collection of models related to various branches of applied mechanics which, like the collection of the Conservatoire National des Arts et M étiers in Paris, contributed to the popularization of technology and applied mechanics.

After London, Chebyshev returned to the French capital where he purchased devices ordered by the Imperial Alexander Lyceum of Saint Petersburg where he used to teach applied mechanics. While he was waiting for instructions from Russia regarding these machines, Hermite took him to visit the physicist L éon Foucault, and they attended his new experiments.25
On his way back to Russia, Chebyshev stopped in Brussels where he visited the museum of applied mechanics. He was particularly attracted by agricultural machines that were displayed there. He then stopped in Berlin where he met Peter Gustav Dirichlet, to whom he presented his work on pure and applied analysis, and with whom he had daily conversations on pure and applied mathematics.
We do not have any detailed report on Chebyshev’s later trips which would be comparable to the one we just summarized, but there is no reason to suppose that his interests and the scientists he met, during these trips, were significantly different from those mentioned in the report on his first trip. We know though that later on, Chebyshev became a faithful participant of the meetings of the Association Française pour l’Avancement des Sciences (French Association for the Advances of Sciences), on which we say a few words now.
The acronym of this society (from the French name) is AFAS. This is a learned society, created in 1872, whose goal was the promotion of science at various levels, establishing links between scientists in several fields, and connecting professional scientists and science amateurs with different backgrounds. Besides the prominent French mathematicians who participated in these meetings like, Gaston Darboux, Georges-Henri Halphen, Hermite, Jacques Hadamard and Henri Poincaré, one finds names of foreign mathematicians too, including Georg Cantor, Cayley, Antonio Cremona, Vilfredo Pareto, Giuseppe Peano, Sylvester and our author, Chebychev. The latter, at some point, was an honorary president of the society. The physiologist Claude Bernard and the microbiologist Louis Pasteur were among its founding members. The society used to hold its meetings every summer, each time in a different city. A new president of the Association was elected every year, and the successive presidents belonged to different fields of sciences. They include the mathematicians Paul Appell (1908), Emile Borel (1925), Elie Cartan (1933) and Paul Montel (1946).
Between the years 1873 and 1882, Chebyshev presented sixteen talks at various sessions of the Association. The written reports of some of these talks are reproduced in his collected works [12][Vol. II, p. 702 to 720]. Among them we can find his reports on the calculating machine and on the cutting of garments, two subjects which we shall consider in more detail below.
Chebyshev’s participation in the 1876 meeting of the AFAS was an opportunity for him to meet the French mathematician Édouard Lucas (1842–1891), known for his work on number theory,26 for his 4-Volume treatise Mathematical Recreations [37], published between 1882 and 1894 (the last two volumes were published posthumously), and of his book Amusing mathematics, published in 1895, also posthumously. These two works played an essential role in promoting among French schoolchildren a passion for the study of mathematics. They also contain extensive notes on the History of Mathematics, in particular on how mathematicians of the past were interested in mathematical recreations.
Lucas later became the director of the Conservatoire National des Arts et Métiers, and one may assume that it is in part due to the warm relationship between the two men that the Conservatoire now owns several machines and models created by Chebyshev. Some of them are exhibited for the general public in the Conservatoire museum. We will now talk in more detail about Chebyshev’s calculating machine.
Chebyshev’s arithmometer
In a talk he gave at the 1876 Clermont-Ferrand meeting of the AFAS, Chebyshev described a calculating machine, which he called arithmometer.27 This first version of his machine performed additions and subtractions. Five years later, at the 1882 meeting, he presented a machine which was further capable of performing multiplication and division. The same year, a description of this machine, titled An arithmetic machine with a continuous motion, appeared in the Revue scientifique de la France et de l’étranger, a French periodical founded in 1863, and which is the ancestor of La Recherche, today’s well-known French magazine for the popularization of science. This article is reproduced in Volume II of Chebyshev’s works in French [12][p. 722-724].
M. d’Ocagne, in his book [42][p. 269-281], gives a detailed description of Chebyshev’s arithmometer, based on explanations that the latter gave him during his last visit to Paris in May of 1893; this was the year before his death.

Lucas, in the third volume of his Mathematical recreations [37], writes about this machine. He recalls that Chebyshev, whom he calls “the most famous number theorist of our times” and who “has honored [Lucas] by his friendship and advices,” presented his machine, which looks like a squirrel cage, at the Clermont-Ferrand session of the Association, the day after a “pilgrimage” they made to the house of Pascal.28 He also declares: “Chebyshev has just deposited with us, for a few months, the only copy of his machine and authorized us to have drawings taken of it which remain on display in the galleries of the conservatory.” The machine remained at the Conservatoire for several years.
Approximation theory
We now turn back to Chebyshev’s theoretical research, namely, approximation theory. This is a theory which provides methods for getting information on general mathematical transformations out of finite data. Typically, one approximates general functions of a real variable by algebraic functions or by trigonometric polynomials. Approximation theory has applications in number theory, extremal problems, and more generally in analysis, computational mathematics, physics and the applied sciences.
![Chebyshev’s arithmometer: Sketches from the paper [4]](http://bhavana.org.in/wp-content/uploads/2021/04/arithmo1.png) |
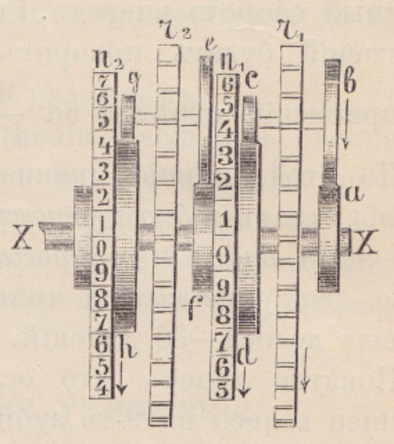 |
![Chebyshev’s arithmometer: Sketches from the paper [4]](http://bhavana.org.in/wp-content/uploads/2021/04/arithmo3.png) |
During the period 1839 -1841, while he was a student in Moscow, Chebyshev wrote an article on iterative methods for finding approximate real solutions of equations, improving upon Newton’s method. The topic of approximation theory was to remain one of his favourites. The paper was published posthumously in [14][Vol. V].
Chebyshev’s first published results on approximation theory are contained in his paper The theory of mechanisms known under the name of parallelograms [12][Vol. I, p. 111-143], published in 1854, in which he addresses the problem of the best uniform approximation of a real-valued function defined on a closed interval by a family of polynomials of bounded degree. In another paper published in the same year, titled On an analysis formula [12][Vol. I, p. 701-702], he used three concepts that lie at the basis of his work in approximation theory: a set of orthogonal polynomials generalizing Legendre polynomials, the method of least squares, and continued fractions. I would like to make a small digression on these three topics.
Orthogonal polynomials are perpendicular with respect to some inner product on a space of functions. They are used in the solutions of several important classes of differential equations, and of other mathematical and physical problems. Typically, such polynomials (to which the names of Legendre, Edmond N. Laguerre, Jacobi, Chebyshev, Hermite, and several later mathematicians are attached), are used as bases for the expansion of general functions. One may compare them to the well-known trigonometric polynomials with which general functions are expanded in Fourier theory. Erwin Schrödinger used orthogonal polynomials in the development of his theory of wave mechanics.
The method of least squares is a technique which allows one to find a function which best agrees (in some precise sense) with some given data. It was developed by Legendre and Gauss at the beginning of the 19th century.
Continued fraction expansion is, initially, a method of approximating a real number by a sequence of rationals, by successive division. The definition is essentially contained in Propositions VII.1, VII.2 and X.2 of Euclid’s Elements:29 contained in Euclid’s Elements, an algorithm to find a common measure for two magnitudes.
For a real number x, one writes
\[x=n_0+r_1\]
where n_0 is an integer and r_1 a real number satisfying 0\leq r_1<1; then, if r_1>0, one writes
\[\frac{1}{r_1}=n_1+r_2\]
with 0\leq r_2<1 and if is r_2>0 one writes
\[\frac{1}{r_2}=n_2+r_3\]
with 0\leq r_3 <1 and so on.
The expression
\[r_0+\cfrac{n_0}{r_1+\cfrac{n_1}{r_2+\cfrac{n_2}{r_3+…}}}\]
is the continued fraction expansion of x. The expansion of x is finite (that is, the above process stops) if and only if x is rational. (This is essentially the way the Greek mathematicians defined incommensurability; see Proposition X.2 of the Elements.) If x is irrational, its continued fraction expansion gives a sequence of rational numbers approximating it, and in some precise sense, also gives the “best” approximation of x by rational numbers. Like real numbers, functions also have continued fraction expansions, and Chebyshev worked with continued fraction expansions of functions. It is useful to recall that continued fraction expansions of functions were extensively used by Euler, who gave explicit formulae for the continued fractions expansion of trigonometric, exponential and other functions. Chebyshev’s Collected Works contain a letter from Chebyshev to Brashman, read in 1865 at the Moscow Mathematical Society, and published in the same year in Liouville’s Journal [12][Vol. 1, p. 611-614]. The letter is titled On algebraic continued fractions and it constitutes a sequel to the article On the interpolation by the method of least squares. In the introduction to the letter, Chebyshev explains to Brashman the use of algebraic continued fractions in interpolation theory, together with the method of least squares.
In 1855, Chebyshev presented to the Saint Petersburg Academy a paper titled On continued fractions [12][Vol. 1, p. 201-230]. The paper was translated into French by Bienaym é and published in Liouville’s Journal in 1858. In this paper, Chebyshev uses the method of least squares, continued fractions and Chebyshev polynomials to obtain an interpolation formula which determines a polynomial function F(x) from its particular values at certain points x_1, …, x_n. Other interpolation techniques are developed in his paper On the interpolation by the method of least squares (1859) [12][Vol. 1, p. 473-498]. We finally mention the paper On interpolation in the case of a great number of data obtained by observation (1859) [12][Vol. 1, p. 387-469] whose title is self-explanatory.
Metric geometry
I would like to say a few words about some notions to which Chebyshev’s name is attached in metric geometry, which is my favourite subject. Let me warn the reader, if necessary, that the notion of metric space as we intend it today, was still unborn at the time of Chebyshev.30 The notions I mention here have been called by his name, because they are close to notions he introduced in analysis, and in particular in approximation theory.
I start with the notion of Chebyshev set. This is usually defined in the context of normed linear spaces. A subset X of a normed space V is called a Chebyshev set if every point in its complement has a unique nearest point in X. Here, a point x in X is a nearest point of a point p in V - X if the distance from x to p is not larger than the distance from x to any other point in X. (In some sense, the point x in X is a “best approximation” of the point p in the complement of X.) A longstanding open problem in this setting, called the “Chebyshev problem”, asks whether any Chebyshev set in a Hilbert space is convex. This problem was studied by N.V. Efimov and S.B. Stečkin in a series of papers published between 1958 and 1961, where the name “Chebyshev set” appeared for the first time. V. Klee showed that in a finite-dimensional normed linear space, the answer is yes if the norm function is smooth. H. Busemann showed that the same result holds in normed linear spaces whose norm function is strictly convex. More generally, he studied Chebyshev sets in the setting of G-spaces whose theory he developed.31 For the interested reader, we refer to the detailed survey on Chebyshev sets by Fletcher and Moors [30]. There is a notion of Chebyshev center of a subset A in a metric space X, a point which, in some precise sense, is a best approximation of the set A in X; there is also a notion of Chebyshev radius of the subset A, and others interesting related notions, see e.g. the papers [40], [41] by T.D. Narang.
Probability
We already mentioned that probability theory was the subject of Chebyshev’s Masters memoir, defended at the University of Moscow. His paper On continued fractions, which we quoted above, contains ideas from this theory. In this paper, for a given function F defined on a certain closed interval of the real line, and given a set of points x_0, x_1,…, x_n in I, Chebyshev searches for a polynomial taking the values F(x_0), F(x_1),…, F(x_n) at these points, with certain conditions satisfied on the difference between the polynomial and the given function. He then considers the same question, with the points x_0, x_1,…, x_n weighted by a discrete probability measure \theta, and this leads him to a sequence of orthogonal polynomials. In the subsequent paper, On the development of functions of one variable [12][Vol. 1, p. 501-508], he considers a continuous setting (he writes: “the points x_i are infinitely close from each other”) where sums are replaced by integrals, and discrete probability measures are replaced by continuous ones. He ends up with functions analogous to Fourier developments.
The notion of mathematical expectation was introduced in the 17th century in the context of game theory initiated by Pascal, Pierre de Fermat and Johann Bernoulli. In his paper titled On mean values [12][Vol. I, p. 687-694], Chebyshev starts by defining this notion in modern terms, and he gives a very wide generalization of Poisson’s theorem on the weak law of large numbers. The name Chebyshev is also associated with the famous Bienaymé-Chebyshev inequality. Roughly speaking, this inequality says that for a very general class of random variables, the probability of taking values that are at a certain relatively large distance from the mean is low. This result is proved in Chebyshev’s paper On mean values, although it was already formulated by Bienaym é fourteen years before. The inequality bears both names. Twenty years after he published this paper, in another article titled On two theorems of probability [12][Vol. II, p. 481-491] (published in Russian in 1887 and in French translation in 1890), Chebyshev presented his method of least squares which, in probability, is equivalent to what we call now the method of moments, and his generalization of the central limit theorem.
It is natural to include among Chebyshev’s achievements in probability theory the fact that outstanding probabilists like A.A. Markov and A.M. Lyapunov were among his students, and were directly inspired by him. The former is considered as the founder of the modern theory of stochastic processes, and the latter is well-known for his theorems on measure theory, dynamical systems and potential theory.
Geography
Another field of applied mathematics in which Chebyshev was involved is geography, and especially cartography, the art of drawing of geographical maps. Let me mention right away that Euler, before Chebyshev, worked extensively in geography. For several years, he had the official title of geographer at the Saint Petersburg Academy of Sciences, and at some point, he was even the head of the geography department there. We refer the interested reader to the article [47] surveying Euler’s work on geography and to the book [8]. In the paper [45], the works of Euler and Chebyshev on geography are included in a much broader context. The recent article [46] is also concerned with Chebyshev’s work on geography.
In 1856, Chebyshev published two papers on cartography carrying the title On the drawing of geographical maps [12][p. 233-236 and 239-247]. The title is the same as that of two papers by Lagrange on this subject, published 77 years before [34]. In these papers, Chebyshev studies the problem of finding maps from the sphere to the Euclidean plane whose distortion is minimal. To give a precise definition of “distortion” is an intricate matter, and Chebyshev relied for this on the work of Lagrange. The fact that there cannot be maps that preserve distances up to scale, from a region of the sphere (representing a country or some part of the earth on a globe) to a region of the Euclidean plane, was known since antiquity. The question of finding maps which have minimal distortion in a certain precise sense has always been the main problem in this field. One of Chebyshev’s achievements was to establish a relation between this problem and Laplace’s equation, reducing the problem of finding the best geographical map to a question in potential theory.
Chebyshev obtained several results on cartography, one among which is the following theorem from [12][p. 242]:
He also gave a method for the computation of this distortion, and he showed, with this theorem in mind, that the search for the best map amounts to the solution of a certain partial differential equation defined on a region with given boundary values. Chebyshev wrote only an outline of the proof of his result. In fact, it happened on several occasions that Chebyshev gave only ideas of proofs; he was never fond of extensive details. Fifty-five years after Chebyshev’s paper on geography was published, (in 1911) Gaston Darboux published a paper carrying the same title as Chebyshev’s, in which he gave the details of the proof of this theorem, based on Chebyshev’s ideas, using the Laplace equation, and applying Green’s formula [16].

A modern proof of Chebyshev’s theorem by John Milnor [38], based on the same ideas, was given about a century after Chebyshev had found his result. Milnor pointed out further developments, and highlighted the importance of the case where the region on the sphere which is mapped is geodesically convex. He writes: “This result has been available for more than a hundred years, but to my knowledge it has never been used by actual map makers.”
To close this section on geography, I would like to quote the following, from the introduction to Chebyshev’s second paper on map drawing, which is an expression of his point of view on the relation between pure and applied mathematics:
The fitting of garments
Chebyshev’s paper On the cutting of garments, published in [12][Vol. II, p. 708], is a report on a talk he delivered at the 1878 session of the AFAS which was held in Paris. According to this report, the idea for this work occurred to him during a communication made two years earlier by Lucas at the meeting of the same association in Clermont-Ferrand. The topic of Lucas’ talk was the geometry of weaving, cf. [36]. The first published version of Chebyshev’s Collected Works contains a summary of this talk, and the complete text of the talk appears in the later version [14][vol. 5, p. 165-170]. A French translation of this extended text is included in the PhD thesis of Anne-Marie Decaillot [18].
For the problem studied by Chebyshev, one starts with a piece of fabric, made of a net of perpendicular threads. We assume that the fabric is designed to take the form of the part of the human body that it is supposed to cover (head, body, etc.). The threads are rigid at the points they intersect, in the sense that the lengths between two consecutive intersection points are fixed, but the angles at these intersections are flexible. Thus, the threads which make initially Euclidean squares become curvilinear parallelograms, after their deformation. The term “Chebyshev net” was given to such a net, made of quadrilaterals of fixed side length. The deformation of the quadrilateral reminds us of the theory of linkages, and Chebyshev made an explicit relation between the problem of fitting of garments and the theory of linkages which were known under the name of parallelograms (see the paper [53]). Several practical problems naturally arise in these considerations, including the question of how close to the form of the human body a piece of fabric can be, or the study of the shape of the optimal curves along which the fabric has to be cut, in order to take a form which is as close as possible to that of the given part of the body for which it is designed. Such questions led to several mathematical developments. In his communication to the AFAS, Chebyshev gave a solution in the form of a differential equation satisfied by the Gaussian curvature of the surface covered by the cloth, and he showed how one can obtain approximate solutions. He studied more particularly the case where the surface that is covered is a hemisphere.
With this work, Chebyshev created a new topic in the geometry of surfaces. The question of the possibility of covering an arbitrary surface with a Chebyshev net became a new mathematical open problem, and it was solved locally in 1926 by Ludwig Bieberbach [3]. Other related problems arose and more general theories of Chebyshev nets were developed in the setting of Alexandrov surfaces, or surfaces of bounded curvature, see e.g. [5] and [2].
Darboux, in his ICM talk in Rome (1908) [15], mentions Chebyshev’s work on the fitting of garments, discussing it from a differential-geometric point of view and making relations with other geometric questions.
The following text is contained in the MacTutor website of History of Mathematics, at the article Chebyshev net and it is attributed to Clive J. Grant. The story might not be authentic, but we quote it because it gives a lively idea of the general atmosphere in which Chebyshev lived.
Part of the paper [44] in which we make connections between works of Euler and of Chebyshev is on the problem of fitting of garments.
Ballistics
A.V. Vassiliev, in his article on Chebyshev [51], says that the latter’s work on approximations of functions, besides being motivated by problems of the theory of mechanisms, was motivated by a problem on ballistics (the motion of bodies that are projected in air). We shall say a few words on this work on ballistics. Let us note, as we already did for several other subjects, that Euler also worked on ballistics. In 1742, he published a 400-page essay on this topic [21], which consists of a commented edition of a book written by the English mathematician and military engineer Benjamin Robins (1707-1751). Besides the problem of ballistics, Euler studied in this book, other related topics, such as the nature of air and fire.
Chebyshev’s work on ballistics is reported in Volume V of the Russian edition of his complete works. An English summary is given in the article [48]. It is reported there that starting from 1856, Chebyshev became a member of the Artillery Committee of the Imperial Russian army, a committee that was in charge of introducing scientific innovations in Russian artillery. He discovered connections between his theoretical work on approximations and ballistics. Three years after his nomination, he was awarded a highly valued medal for his “three-year long meticulous and useful work, apart from performing his direct duties at the Academy of Sciences, on mathematical research at the Artillery Committee, a work which has proved so beneficial for the development of rifle guns and shells.” A document, extracted from the Saint Petersburg Military Scientific Council of 1863, explaining the difficult problems of artillery that need to be solved using mathematical tools, and in particular, Chebyshev’s work on this topic, is translated and reproduced in the Russian collected works [14][Vol. 5, p. 239]. In this document, we read:
Chebyshev’s results in the field, reported on in the document mentioned, include an explanation of the role of rotary motion in shell fire and the study of the optimal shape of a shell.
Among the prominent French mathematicians who worked on artillery, we can mention Legendre, Laplace, Lagrange and Poisson, and there are others.32
Chebyshev as a teacher
We read in the biography contained in [12][Vol. II, p. v] that Chebyshev, as a teacher, was “pedantically rigorous”. He never missed a class, never arrived late to the classroom, and on the other hand, he never stayed even for one minute after the official time was over, even if he had to interrupt the lesson, in the middle of an argument. If a proof was not completed, he would start, at the next lesson, at the same point where the proof was interrupted. Before doing a calculation on the blackboard, he used to give an explanation on its purpose, but he always did the calculation silently, and the students were expected to check the details without hearing him talking.
His lessons were accessible and easy to follow, and they were systematically interrupted by digressions in which he reported on other mathematician’s points of view on the question discussed. Furthermore, on each such occasion, he used to give details on his visits to foreign countries. This made the class more lively, and the digressions aroused a certain interest from the students. We also learn that regarding examinations, he was neither too severe nor too indulgent, and that he remained extremely restrained and courteous. As an examiner during dissertation defenses, his questions were always of a general nature; he never tried to embarrass the candidate.
Youschkevitch’s article [52] contains the following translation from the Russian of a description by Lyapunov of the stimulating atmosphere he found in a course on probability theory which he attended in the late 1870s:
We also learn from the biography in [12][Vol. II] that Chebyshev continued to meet his former students after their graduation, especially guiding those who remained in mathematics. Once a week, his door was open for all those who wanted to inform him about the subject of their studies and for others who wanted to have indications from him.
Among Chebyshev’s students, we mention A.A. Markov (1856–1922), A.M. Lyapunov (1857–1918), K.A. Poss é (1847-1928), A.N. Korkin (1837–1908), E.I. Zolotarev (1847–1878) G.F. Voronoi (1868–1908), and D.A. Gravé (1863-1939) (the latter was a student of Chebyshev and Korkin). We also mention V.A. Steklov (1864–1926), who was a student of Lyapunov, N.G. Chebotarev (1894-1947), N.I. Akhiezer (1901-1980) and B.N. Delone (1890-1980) who were students of Gravé, A.D. Alexandrov (1912-1999), the founder of the outstanding Russian school of metric geometry, who was a student of Delone, and A.S. Besicovitch (1891-1970), a student of Markov whose name is associated with the notion of Hausdorff-Besicovitch dimension. For several decades, the mathematical chairs in Saint Petersburg were occupied by Chebyshev’s students, or by mathematicians who worked on questions he posed and who were strongly influenced by his works and by his view that mathematics should be motivated by concrete practical problems. By the end of the nineteenth century, the mathematical school he founded in Saint Petersburg, in which a multitude of specialties was represented, became the principal one in Russia, and it was also one of the most important ones in the world. His influence on mathematics went beyond the city of Saint Petersburg. Some of his descendants founded schools in various places: Grav é in Kiev, Akhiezer in Kharkov, Lyapunov in Kharkov and then also in Odessa. Besicovitch taught in Cambridge. All these descendants perpetuated Chebyshev’s tradition, working on problems he formulated and developing his theories. For example, Markov, Zolotarev, Grav é and Akhiezer made important contributions to extremal problems and the approximation of functions by polynomials, starting with problems that Chebyshev formulated; see [31]. In probability theory, A.A. Markov, starting in 1900, published a sequence of papers in which he extended Chebyshev’s study of sequences of independent random variables to include certain types of dependent random variables, setting the bases of the theory of Markov chains. Markov and Lyapunov are the main representatives of the probability school founded by Chebyshev. One could write a book in several volumes on the influence of Chebyshev on later Russian mathematicians.
Finally, regarding teaching, one should mention that during several years, Chebyshev was a member of a committee of the Russian Ministry of Education in charge of establishing programs for mathematics, physics and astronomy in secondary schools, and the supervision of textbook writing for school pupils.
On the spelling of the name Chebyshev
There are many ways of transliterating Chebyshev’s name from the Cyrillic into Latin characters. One can find in the literature the variants Chebychev, Tchebycheff, Tchebychev, Tschebyscheff, Tchebyshev, Chebyschev, Chebycheff, Tchebysheff, Tchebyscheff, Tschebychev, Tschebycheff, Chebysheff, and there are several others. In fact, the unique way in which Chebyshev wanted his name to be transliterated is Tchebichef. This was also the spelling which he used in signing the papers he published in French. Maurice d’Ocagne wrote a note concerning this matter, published in the Bulletin des sciences math ématiques, titled “On the spelling of the name of Tchebichef” [43], and it is interesting to quote it here (in English translation):
During his last stay in Paris, in May 1893, the illustrious Russian geometer accepted to entrust me with the task of writing a complete description (which had never been given even in Russian) of his intriguing arithmetic machine, a description which he reviewed himself with the greatest care.
On this occasion, he personally prescribed the French spelling of his name under the form “Tchebichef”, formulating the wish that it is exclusively adopted in all his writings written with our characters. It is because he recommended me to ensure his desideratum regarding this point, from which common usage deviates, that the preceding lines have been written.
Evidently, Chebyshev’s wish was not fulfilled.
The last years
Chebyshev spent a quiet life, dedicated to mathematics. He never married. In 1882, he resigned from university in order to devote his time to research at the Academy of Sciences, while he kept traveling to France, almost every summer. From the report of the 1883 session of the AFAS [1], we learn that Chebyshev (who was a honorary president of this society) gave four lectures at that session, on four different topics, titled (1) On the rectification on curves; (2) On the arithmometer; (3) On the choice of the radius in definite integrals taken along a circle and by which are expressed the probabilities according to their generating functions; (4) On the functions whose derivative of a certain order is as much as possible far from zero. We also learn that during the same session, Chebyshev participated in a discussion on the mathematical meaning of the Atlantide myth in Plato’s Timaeus.
Until his last years, Chebyshev continued to build mechanical engines. His biographer in [12][Vol. II, p. iii] tells us that when he settled in Saint Petersburg, in 1847, his salary as an Adjunct Professor was modest, which made him very frugal, and that he remained so throughout his lifetime, except for one thing for which he never spared his money, viz. the elements he needed to construct his mechanical models, for which he was capable of spending hundreds of thousands of roubles.
Chebyshev’s contribution to science was acknowledged early in his career and he was a member of most European academies of sciences and learned societies. In particular, he was the first Russian to be admitted to the Paris Academy of Sciences since Peter the Great.33 He kept until the end of his life close friendly relations with Hermite, Bertrand, Catalan, Leopold Kronecker, Charles-Ange Laisant, Lucas and other mathematicians from Western Europe. Vassiliev’s article [51] is dedicated to Charles Hermite, “in memory of his friend Chebyshev”.
Chebyshev submitted his last paper to the Academy of Sciences at the age of seventy-three. A few months later, on the 8th of December 1894, he died unexpectedly of a heart attack at his desk, while he was discussing with Grav é. After this conversation, the latter wrote a note from memory, on behalf of his teacher, titled A rule for the approximate rectification of arcs, in which he summarised what he heard from him. This is a topic on which Chebyshev worked for several years. In fact, it even was the title of a lecture he gave at the 1882 session of the AFAS. Gravé’s note was published in 1895, in the Bulletin of the Academy of Saint Petersburg. A few days after Chebyshev’s death, Markov wrote a letter to Hermite, containing a result of his mentor on the prime divisors of numbers of the form 1+4n^2. Hermite presented the letter to the French Academy of Sciences and it was published in the Comptes Rendus [39].

There are several good biographical articles on Chebyshev. We recommend the ones contained in Volume II of Chebyshev’s collected papers in French [12] and in Volume V of his collected works in Russian [14], the article by Delone in his book [19], the paper P. Tch ébychef and his scientific work by Vassiliev [51], the article by Youschkevitch in the Dictionary of Scientific Biography [52] and the articles by Butzer and Jongmans [6], [7].
In guise of a conclusion
Chebyshev liked concrete problems, and he wanted each mathematical existence result to be accompanied by an algorithm to find the object whose existence is claimed. Vassiliev reports on a conversation he had with Chebyshev some years before his death, in which the latter expressed his general view on the aim and problems of mathematics. He recalls the following statement by Chebyshev:
- Association française pour l’avancement des sciences, Bulletin des sciences mathématiques et astronomiques, 2e série, t. 7 (1883), no. 1, p. 181-192.
- I.Y. Bakelman, Chebyshev nets in manifolds of bounded curvature, Trudy Math. Inst. Steklov. 76 (1965) 124-129. Translated in: Two-dimensional manifolds of bounded curvature. Edited by A.D. Aleksandrov and V.A. Zalgaller. Proceedings of the Steklov Institute of Mathematics, No. 76 (1965) American Mathematical Society, Providence, R.I. 1965.
- L. Bieberbach, Über Thebychefsche Netze auf Flächen negativer Krümmung, sowie auf einigen weiteren Flächenarten. Preuss. Akad. Wiss., Phys. math. Kl. 23, 294-321.
- V.G. von Bool, Chebyshev’s arithmometer, Proceedings of the science office of the society of lovers of natural sciences, Imperial University of Moscow (1894) v. 7, no. 1, p. 13-22.
- Y.D. Burago, S.V. Ivanov, and S.G. Malev, Remarks on Chebyshev coordinates, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI), 329 (Geom. i Topol. 9) 195 (2005) 5-13.
- P. Butzer and F. Jongmans, P. L. Chebyshev (1821-1894) and his contacts with Western European scientists. Historia Math. 16 (1989), no. 1, p. 46-68.
- P. Butzer and F. Jongmans, P. L. Chebyshev (1821-1894). A guide to his life and work. J. Approx. Theory 96 (1999), no. 1, p. 111-138.
- R. Caddeo and A. Papadopoulos (ed.) Spherical geometry and geography in the eighteenth century: Euler, Lambert and Lagrange, Springer, 2021.
- K. Chandrasekharan, Introduction to analytic number theory, Grundlehren der mathematischen Wissenschaften 148, Springer Verlag, New York, 1968.
- P.L. Chebyshev, An essay on an elementary analysis in probability theory (Russian), Magister thesis, University of Moscow, 1845, 66p.
- P.L. Chebyshev, Theory of congruences (Russian), Saint Petersburg, 1949, 2nd ed., 1879. German translation: Theorie der Congruenzen, Berlin, 1888. Italian translation: Teoria delle congruenze, Rome, 1895.
- P.L. Chebyshev, Œuvres (French), edited by A. Markov and N. Sonin, Imprimerie de l’Acad émie Imp ériale des Sciences, Saint Petersburg, 2 volumes, 1899-1907.
- P. L. Chebyshev, Sochinenia (Writings, in Russian), edited by A. Markov and N. Sonin, Imprimerie de l’Académie Impériale des Sciences, Saint Petersburg, 2 volumes, 1899-1907.
- P.L. Chebyshev, Complete Collected Works (Russian), 5 volumes, edited by I.I. Artobolevsky, S.N. Bernstein, N.G. Bruevich, I.M. Vinogradov, B.N. Delone, V.L. Goncharov, A.N. Kolmogorov, A. Krylov, L.S. Leibenson, V.I. Smirnov and S.L. Sobolev, Izdatel’stvo Akad. Nauk SSR, Moscow-Leningrad, 1946-1951.
- G. Darboux, Les origines, les méthodes et les problèmes de la géométrie infinitésimale. Proceedings of the IVth ICM, Rome. Vol. 1, p. 105-122, 1909.
- G. Darboux, Sur la construction des cartes géographiques, Bulletin des sciences mathématiques, 35 (1911), p. 23-28.
- P.J. Davis, The thread: A mathematical yarn, Birkhäuser, Boston-Basel-Stuttgart, 1983.
- A.M. Decaillot, Géométrie des tissus. Mosaiques. Échiquiers. Mathématiques curieuses et utiles. Revue dhistoire des math ématiques, 8 (2002), p. 145-206.
- B.N. Delone, the St. Petersburg school of number theory, 1947. English translation published by the AMS and the London Mathematical Society, History of Mathematics series, Vol. 26, Providence, Rhode Island, 2005.
- L. Euler, Variae observationes circa series infinitas, Commentarii academiae scientiarum Petropolitanae 9, p. 160-188 (1744). Opera Omnia, Series 1, vol. 14, p. 217-244.
- L. Euler, New principles of gunnery, London, 1742. German edition, Neue Grundsätze der Artillerie, 1745. Opera Omnia, Series 2, Volume 14, p. 1-409.
- L. Euler, D écouverte d’une loi tout extraordinaire des nombres par rapport à la somme de leurs diviseurs, Bibliothèque impériale 3, p. 10-31 (1751). Opera Omnia, Series 1, vol. 2, p.241-253.
- L. Euler, Discussion plus particulière de diverses manières d’élever de l’eau par le moyen des pompes avec le plus grand avantage, Mémoires de l’Académie des Sciences de Berlin, Volume 8 (1754), p. 149-184. Opera Omnia, Series 2, Volume 15, p. 251-280.
- L. Euler, Maximes pour arranger le plus avantageusement les machines destinées à élever de l’eau par le moyen des pompes, Mémoires de l’Académie des Sciences de Berlin 8, 1754, p. 185-232. Opera Omnia: Series 2, Volume 15, p. 281-318.
- L. Euler, Théorixe plus compléte des machines qui sont mises en mouvement par la réaction de l’eau, Mémoires de l’Académie des Sciences de Berlin, Volume 10 (1756), p. 227-295. Opera Omnia, Series 2, Volume 15, p.157-218.
- L. Euler, Sur l’action des scies, Mémoires de l’Académie des Sciences de Berlin 12 (1758), p. 267-291. Opera Omnia, Series 2, Volume 17, p. 66-88.
- L. Euler, Recherches plus exactes sur l’effet des moulins à vent, Mémoires de l’Académie des Sciences de Berlin 12, 1758, p. 165-234. Opera Omnia: Series 2, Volume 16, p. 65-125.
- L. Euler, De repraesentatione superficiei sphaericae super plano, Acta Academiae Scientarum Imperialis Petropolitinae (1778), p. 107-132, Opera Omnia, Series 1, Volume 28, p. 248-275.
- L. Euler, Index systématique et raisonné des oeuvres arithmétiques d’Euler par MM. Bouniakovsky et Tchébychef. Leonh. Euleri Commentationes arithmeticae collectae, vol. I and II, 1849.
- J. Fletcher and W.B. Moors, Chebyshev sets, J. Aust. Math. Soc. 98 (2015), no. 2, p. 161-231.
- V.L. Goncharov, The theory of best approximation of functions, Translated from the 1945 Russian original by Olga Holtz and Vladimir Yegorov. J. Approx. Theory 106 (2000), no. 1, p. 2-57.
- D.A. Gravé, Sur la construction des cartes géographiques, Journal de mathématiques pures et appliquées 5e série, 2 (1896), p. 317-362.
- D.A. Grav é, Sur un théorème de Tchébychef généralisé, Journal für die reine und angewandte Mathematik 40 (1911), No. 4, p. 247-251.
- J.-L. de Lagrange, Sur la construction des cartes géographiques, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-lettres de Berlin, année 1779, Premier mémoire, In: Œuvres complètes, tome 4, p. 637-664. Second mémoire Œuvres complètes, tome 4, p. 664-692.
- A.-M. Legendre, Théorie des nombres, 3d. edition, Paris, Firmin Didot, 1830.
- E. Lucas, Lois géométriques des tissages, Congrès de l’Association Française pour l’Avancement des Sciences 5 (1876), p. 114.
- E. Lucas, Récréations mathématiques, Gauthier-Villars, Paris, 1882-1894.
- J. Milnor, A problem in cartography, The American Mathematical Monthly, Vol. 76, No. 10 (Dec. 1969), p. 1101-1112.
- A. Markoff, Démonstration d’un théorème de Tchébycheff (extrait des papiers laissés par l’auteur). Lettre adressée à M. Hermite, C. R. Acad. Sc. Paris 120 (1895), p. 1032-1034.
- T.D. Narang, A result on Chebyshev centres, Mat. Vesnik 38 (1986), no. 2, p. 197-198.
- T.D. Narang, Convexity of Chebyshev sets in linear metric spaces, Bull. Calcutta Math. Soc. 102 (2010), no. 1, p. 43-46.
- M. d’Ocagne, Le calcul simplifié par les procédés mécaniques et graphiques, Gauthier-Villars, Paris, 1894.
- M. d’Ocagne, Sur l’orthographe du nom de Tchebichef, Bull. Sc. Math. 55 (1931), p. 98.
- A. Papadopoulos, Euler and Chebyshev: From the sphere to the plane and backwards, Proceedings in Cybernetics (A volume dedicated to the jubilee of Academician Vladimir Betelin), 2 (2016) p. 55-69.
- A. Papadopoulos, Quasiconformal mappings, from Ptolemy’s geography to the work of Teichmüller, In: Uniformization, Riemann-Hilbert Correspondence, Calabi-Yau Manifolds, and Picard-Fuchs Equations (ed. L. Ji and S.-T. Yau), International Press and Higher Education Press, ALM 42,. 2018, p. 237-315.
- A. Papadopoulos, Map drawing and foliations of the sphere. Proc. Conf. dedicated to P.L. Chebyshev, Obninsk, May 14, 2019, ed. V. Galkin, Russian Journal of Cybernetics 1 (2020), p. 42-49.
- A. Papadopoulos, Mathematics and map drawing in the eighteenth century. To appear in Gaṇita Bhārātī.
- V. Prokhorov, Pafnuty Chebyshev: To mark the 175th anniversary of his birth, Teor. Veroyatnost. i Primenen. (1996) 41 No. 3, p. 613-627. English translation: Theory Probab. Appl. (1996) 41 No. 3, p. 519-530.
- S. Ramanujan, A proof of Bertrand’s postulate, Journal of the Indian Mathematical Society 11 (1919), p. 181-182.
- M. Rubinstein and P. Sarnak, Chebyshev’s bias, Exper. Math., 3 (1994), p. 173-197.
- A. Vassilief, P. Tchébychef et son oeuvre scientifique, Bollettino di bibliografia e storia delle scienze matematiche, I Turin, 1898.
- A.P. Youschkevitch. Chebyshev in Dictionary of Scientific Biography, vol. 3, Charles Scribner’s sons, New York, 1st ed., 1970, several later editions.
- A. Zhukova, Math and Motion: A look at Chebyshev’s works on linkages, in this issue of Bhāvanā.
Footnotes
- We are giving Chebyshev’s date of birth according to the Gregorian calendar, which is the one universally used today. Some sources give different dates, because they use the Julian calendar, which was the official one used in 19th century Russia. In Chebyshev’s time, a date according to the Julian calendar was 12 days behind its corresponding Gregorian date. Since 1901, the difference between the two calendars is 13 days. Russia adopted the Gregorian calendar on January 24th 1918, after the October Revolution. ↩
- Obninsk is one of the “science cities” that were built in Russia in the 1940s. It hosts 12 science and technology research institutes (physics, chemistry, meteorology, etc.). In 1954, the world’s first nuclear power plant, generating electricity on a large-scale started operating there. ↩
- For example, V.Y. Bunyakovsky, A.N. Korkin and M.V. Ostrogradsky studied in Paris, S.V. Kovalevskaya studied in Heidelberg, Berlin and Göttingen. ↩
- N.D. Brashman (1796–1866) was a mathematician of Czech origin who, after graduating from Vienna’s Polytechnic Institute, emigrated to Russia. He taught for nine years at the University of Kazan, where he was a colleague of N.I. Lobachevsky, the main founder of hyperbolic geometry. Brashman was appointed Professor of Applied Mathematics at the University of Moscow in 1834, three years before Chebyshev enrolled there as a student. He had specialized in mechanics, especially hydrodynamics, using the principle of least action extensively in his theoretical works. He was also knowledgeable in probability theory and in the theory of integration of algebraic functions. The young Chebyshev was certainly influenced by Brashman’s teaching on these topics, many of which later on became a part of his own principal fields of investigation. Brashman was also a founding member, and the first president of the Moscow Mathematical Society, of which Chebyshev became one of the first members. ↩
- Before the 1917 revolution, the candidate degree in Russia was the first academic degree, and it was obtained after the completion of a memoir. It is comparable to a Masters degree today. After the revolution, university studies were reorganized and candidate became (and is still today) the name of a higher degree, which is comparable to a PhD in the rest of the world today. ↩
- This journal, one of the oldest French mathematical journals, as also of the world as well, was founded in 1836 by Joseph Liouville, with whom Chebyshev later on had very strong relations. The journal was usually referred to as Liouville’s Journal. Between 1843 and 1873, Chebyshev published 17 papers in this journal. ↩
- In this paper, all the translations from the French are ours. ↩
- This is a degree that existed in Russia before the revolution, and which stood between the candidate degree and the doctorate. ↩
- A pro venia legendi is a dissertation which allows students to teach at a university. It is different from a doctorate, and could be attained before the doctorate. ↩
- The dissertation was published posthumously. It is contained in the Russian edition of his Collected Works [Vol. V]. A French summary of this dissertation is contained in the French edition [12][Vol. II, p. xix-xx]. ↩
- V.Y. Bunyakovsky (1804-1889) was a professor at the University of Saint Petersburg and a member of the Saint Petersburg Academy of Sciences. He was a specialist in theoretical mechanics and number theory. He had studied in Paris, where he obtained his doctorate under Cauchy. ↩
- I.I. Somov (1815-1876) was a specialist in applications of analysis to kinematics. He developed a geometric approach to theoretical mechanics. He was knowledgeable in history, and in particular, in the history of mathematics. ↩
- Legendre made these assertions by examining tables of prime numbers. ↩
- In this paper, we use Chebyshev’s notation \log x for natural logarithms (instead of the more common \ln x). ↩
- Chebyshev refers here to the statement suggested by Legendre in his Number theory (vol. 2, p. 65 of the 3rd edition), saying that the limit of \varphi(x) is \frac{x}{\log x -1.08366}. If this were true, it would imply that the limit of \frac{x}{\varphi(x)}-\log x is -1.08366, contradicting a result of Chebyshev that we mention in the sequel.} ↩
- The mathematician Paul Heinrich Fuss (1797–1855) was the permanent secretary of the Academy of Science of Saint Petersburg, having succeeded in 1826 his father, the mathematician Nicolas Fuss (1755–1826). Nicolas himself had been a much younger colleague of Euler, and probably his favourite collaborator too. He also married Euler’s grand-daughter Albertine. Thus, Paul Heinrich Fuss was Euler’s great-grandson. ↩
- The rank of extraordinary professor is lower than that of ordinary professor (which is the highest rank). This denomination is still used in Italy, Belgium and probably in other countries as well. ↩
- Joseph Bertrand (1822-1900) noted that this assertion is true for n\leq 6\times 10^6, which was the extent of the tables of prime numbers that were available at that epoch (Journal de l’ école Polytechnique, 1845, cahier XXX). ↩
- In Chapter VII of his monograph [9], K. Chandrasekharan studies this function, which he calls the Chebyshev function. ↩
- The dates indicated in the report are June 12 to November 7, which means June 24 to November 19, according to the Gregorian calendar. ↩
- The Conservatoire National des Arts et Métiers in Paris is one of the higher-education schools that were created during the French Revolution (the other two being the École Polytechnique and the École Normale Supérieure). It hosts a science museum where, several years later, some of Chebyshev’s own machines were displayed. ↩
- James Watt (1736-1819) played a major role in the 19th century industrial revolution. In the steam engine of Watt, there is a linkage transforming a straight-line motion into an approximate circular one, which Chebyshev calls Watt’s Parallelogram. The discovery of that linkage acted as a motivation for his later work on approximation theory and on what became known later as the theory of linkages; see the report in [53], in the present issue. ↩
- Jacques de Vaucanson (1709-1782) was a French inventor, artist and mechanical engineer. He constructed several mechanical devices, including automatic music players of the size of a human being, and a “digesting duck” capable of eating grains, then metabolising and defecating them. Vaucanson’s automata are displayed in museums and they inspired many engineers. It is not surprising that Chebyshev, who was a passionate designer of mechanical constructions, was extremely interested in Vaucanson’s works. ↩
- The mathematician and philosopher Blaise Pascal (1623-1662) is considered the first constructor of a mechanical calculating machine, which he called “arithmetic machine” (machine arithm étique). Later on, the machine was called “Pascaline”, or “Pascaline Wheel”. Pascal, who began working on this machine at age 19, was motivated by the desire to help his father in his calculations. The latter was a supervisor of taxes in the city of Rouen. Pascal received a “privilege” from Louis the XIVth, the king of France, which guaranteed him the exclusive right to make and sell such machines. After Pascal’s death, Gottfried W. Leibniz worked on improving the calculating machine. It took Leibniz 40 years before he was satisfied with his effort. Two centuries after Leibniz, Chebyshev invented a new type of arithmetic machine, known as “arithmometer”. ↩
- The original Foucault pendulum was part of the collection of the Conservatoire National des Arts et M étiers in Paris. ↩
- The name Édouard Lucas is associated with Lucas numbers, which are related to Fibonacci numbers by a recurrence relation. A famous conjecture says that there are infinitely many prime Lucas numbers. ↩
- In Greek, arithmon means number and metron means to measure, or to count. ↩
- The 187th meeting took place in Clermont-Ferrand, which is the city where Pascal was born and where he lived for several years. Today, a museum there hosts objects that belonged to him, including a Pascaline. ↩
- More precisely, the notion of continued fraction is a special case of Anthyphairesis. ↩
- The axioms of a metric space were formulated by Maurice Fr échet in 1906. ↩
- G stands for geodesic, and G-spaces in the sense of Busemann are metric spaces satisfying certain axioms concerning existence, extendability, etc. of geodesics. ↩
- We mention by the way that the école Polytechnique, where Legendre, Laplace, Liouville, Joseph Fourier, Gaspard Monge, Cauchy, Hermite, Hadamard and other prominent mathematicians taught, is a military school. ↩
- The mention of Peter the Great is not a coincidence. The emperor was interested in all domains of science and technology. He made several visits to France, Holland and other counties of Western Europe during which he visited factories, shipyards, observatories, printing houses, museums, libraries, carpentries, hospitals, and other institutions. He was interested in all these skills, and his desire was to establish similar structures in his country. Some of his visits to the West lasted several months, which of course was very unusual for a monarch. In particular, he was absent from Russia during the whole period January 1716 to October 1717. During this period, he spent several weeks in France including 45 days in Paris. In June 1717, the Russian tsar made another stay in the French capital during which he met several mathematicians and physicists, and besides the factories, foundries and other workshops in which he was still very much interested, he visited the observatory, the Sorbonne and other important academic institutions. He bought a large quantity of science instruments. On June 19, 1717, Peter made a visit to the French Academy of Sciences and he discussed with the academicians, who were all impressed by his knowledge. A few weeks later he was elected unanimously member hors de tout rang at the French Academy. ↩
- Chebyshev (and Vassiliev) refer here to the Greek literature concerning the duplication of the cube. This problem is one of the famous Greek construction problems. It is equivalent to the problem of constructing the magnitude \sqrt[3]{2} by ruler and compass and it was solved only in the 19th century. The ancient references on this problem include Theon of Smyrna’s Mathematics useful for the understanding of Plato (2nd century AD) and Plutarch’s On the letter “E” at Delphi (1st-2nd century AD). We read in these references that when Apollo, the Greek deity, asked that his altar at Delos should be doubled, “a matter requiring the most advanced geometry”, his aim was not enjoying a larger altar but he was rather “putting his strong command upon the Greeks to practice geometry.” ↩
