Sarvadaman Chowla: The Perpetual Ambassador for Number Theory

Chowla was born on 22 October 1907 in London, England. His father, Gopal Singh Chowla held a faculty position in Mathematics at the Government College, Lahore. At the time of Sarvadaman Chowla’s birth, Gopal Singh Chowla and his wife, Shakuntala, were in England as he was preparing for the Mathematics Tripos at Trinity College, Cambridge. They returned to Lahore soon afterwards, where Chowla grew up. Naturally, he showed an interest in mathematics. He had a sister, Usha, and a younger brother, Inder. Inder also developed an interest in mathematics, and obtained his PhD from Cambridge in 1942 under the supervision of H. Heilbronn. Unfortunately, Inder passed away in 1943 at a relatively young age.

Making of a mathematician

Chowla started showing a predisposition for mathematics from a young age, and must have been encouraged by his mathematician father. Another “enabler” for his mathematical talent was the Journal of the Indian Mathematical Society (JIMS) where we find his first recorded mathematical publication at age 17. This journal, functioning since 1907,¹ was an avenue that aided many Indian mathematicians, especially from the early to mid twentieth century, to communicate their latest research. What’s more, the journal published questions posed by individuals, solutions to these questions, and short mathematical notes, all of which could arise from thinking deeply about these questions. For example, these notes could contain a newer, and simpler proof of a known result, or spoke of general ideas arising from the above solutions.

Chowla started publishing questions in the JIMS, as well as solutions to questions posed by others, while still in his teens. From this, he graduated to writing short notes inspired by questions that held his interest. Some of the themes in these problems and solutions grew into his long-standing research interests, even as the young teenager grew up to become a professional mathematician. In an introduction to the Collected Papers of Chowla [8], James Huard [15] points out that Chowla’s name first appears in print in August 1924 in the JIMS when he was 16. He posed two questions in Volume 15 of the journal [4], both related to values of infinite products and infinite sums.

• Question 1346: If |x| < 1, prove that
  \left\{\frac{(1 - x^{2})(1 - x^{4})(1 - x^{6})\cdots}{(1 - x)(1 - x^{3})(1 - x^{5})\cdots}\right\}^8 = \sum_{r=1}^{\infty} \frac{r^3 x^{r-1}}{1 - x^{2r}}.

  From this, deduce that if n is an odd, positive integer, then the number of representations of n as the sum of eight squares is 16 times the sum of the cubes of its divisors.

  We would like to make a remark here that the representation of a positive integer as a sum of a certain number of squares or cubes, or more generally, of k-th powers, has always been an important topic in number theory.

  More precisely, let r_{s,k}(n) denote the number of representations of n as a sum of s positive k-th powers. The numbers r_{s,k}(n) often show up as coefficients in the power-series of an important class of functions called “modular forms”. Inspired by a problem posed by Edward Waring in 1770, substantial contributions were made in the 1920s to questions about the asymptotic behaviour of r_{s,k}(n). In 1918, Hardy and Ramanujan introduced the fundamental circle method to address the partition function p(n) (in other words, r_{s,1}(n), which denotes the number of representations of n as a sum of natural numbers less than or equal to n). After the early demise of Ramanujan, the circle method was further developed by Hardy and J.E. Littlewood in the 1920s to study r_{s,k}(n) for k>1. Littlewood later became Chowla’s PhD advisor. Among the results in Chowla’s PhD thesis was an important observation about the growth of r_{3,3}(n) as n\to\infty. Question 1346 in the JIMS demonstrates that he had started thinking about such questions at a very young age. The other question posed by him in [4] is as follows:

• Question 1348:
  Prove that

  \sum_{n=0}^{\infty} \frac{(2n+1)e^{-(2n+1)\pi}}{1 + e^{-(2n+1)\pi}} = \frac{1}{24}.Prove that

  \sum_{n=1}^{\infty} \frac{n^5e^{-2n\pi}}{1 - e^{-(2n)\pi}} = \frac{1}{504}.

  In 1929, Chowla himself answered this question in JIMS [7], using identities from Georges Halphen’s “Fonctions Elliptiques”. Chowla’s interest in elliptic functions would later lead to interesting results, including important joint results with Atle Selberg.

As Huard points out, both the above questions were clearly inspired by the work of Ramanujan. This is a perfect example of how the mathematical thoughts of a few people can influence a much larger community of mathematicians, each of whom takes these ideas forward using their own approach and training.

The first solution given by Chowla to a publicly-posed problem appeared in print in 1925 [5]. He answered a question of K.J. Sanjana. ² The question was to show that the equation

y^3 = 6x^2 + 2has no integer solutions other than x = 1 and y=2.

Chowla provides two solutions to the above problem, one exclusively on his own [6], and another with S. Audinarayanan and I. Totadri Iyengar [5]. In both cases, the above deduction is made as an almost immediate consequence of the fact that the equation

x^3 + y^3 = z^3does not have non-trivial integer solutions.³

Over the next six years, Chowla continued to publish solutions to problems posed in the JIMS. Interestingly, some of these questions had been posed by Ramanujan a few years earlier. Other questions that he answered were either posed, or simultaneously solved by his contemporary mathematicians including T. Vijayaraghavan, R. Vaidyanathaswamy, K. Ananda Rau, and of course, S. Sivasankaranarayana Pillai with whom he developed a formidable collaboration, and a deep friendship.

Chowla started publishing mathematical papers in Indian and international journals in the year 1926. Topics that interested him were dominant research themes at that time: convergence of special types of series, evaluation of elliptic integrals, Eulerian and Bernoulli numbers, identities related to the zeta function, properties of arithmetic functions such as the divisor function and the Euler-\phi function (more details in the next section), the function r_{s,k}(n), continued fraction expansions for irrational numbers, and class numbers of binary quadratic forms. The topic of class numbers developed, in later years, “into a singular theme running through all of Chowla’s papers’’[18].

He received his Master’s degree from Punjab University in Lahore in 1928. By this time, he was an active researcher. In December of 1928, he attended a conference of the Indian Mathematical Society, and delivered lectures on three of his then recent publications in the JIMS [9], [10], [11].

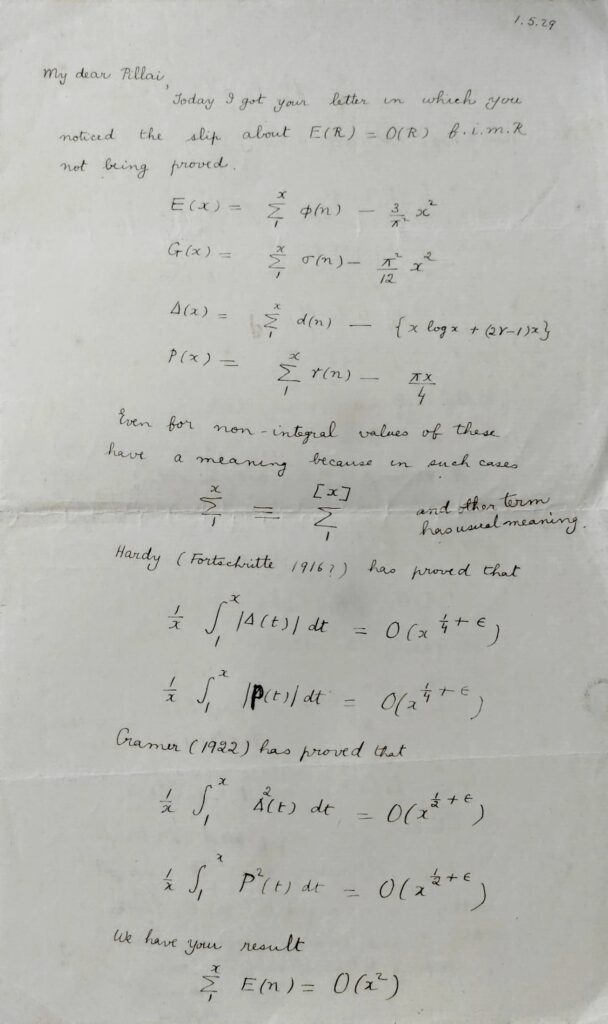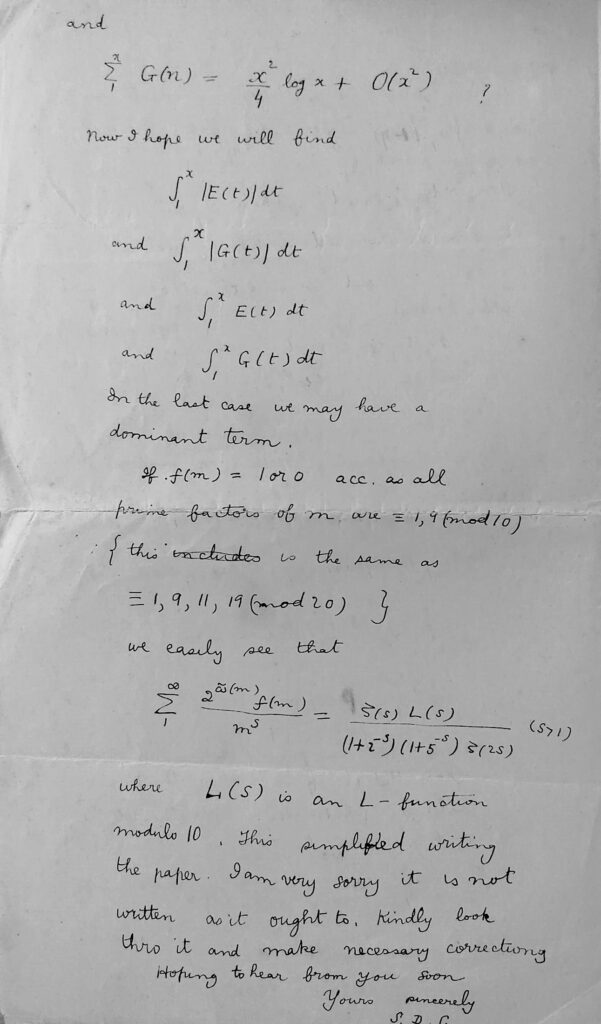Chowla’s 1929 letter to Pillai courtesy: R. Thangadurai

In July 1929, Chowla travelled to Europe, with the plan of travelling across the continent and starting his doctoral studies at the Trinity College, Cambridge later that year. He was accompanied by his father. During his travels across the continent, he enthusiastically continued to think about mathematics, and corresponded regularly with Pillai on some of his favourite topics.

In an unfortunate turn of events, Chowla’s father succumbed to pneumonia in Paris in December, 1929. This must have been a difficult time for Chowla as he faced this sudden and unexpected bereavement all alone, far away from his family. Undeterred, he continued with his doctoral studies under the supervision of the famous number theorist Littlewood (whose work on Waring’s problem has already been mentioned before), and submitted his thesis in 1931. The impeccably hand-written thesis has three parts, each of which addresses a distinct question.

In the first part of the thesis, titled Contributions to the analytic theory of numbers (I), Chowla finds estimates for the first and second moments of error terms which show up in the asymptotic distribution of some fundamental arithmetic functions which had been of interest to him for several preceding years. “The proof of this result lies rather deep’’, he asserts confidently in the introductory paragraph. In the second part, titled Contributions to the analytic theory of numbers (II), he studies r_{3,3}(n), the number of representations of a natural number n as a sum of three cubes, and also r_{3,4}(n), the number of representations as a sum of three fourth-powers. In the third part, titled Two problems in the theory of lattice points, Chowla obtains new estimates for the number of lattice points (points with integer coordinates) inside ellipsoids of bounded size.

Although Chowla did not meet Littlewood frequently, he worked on topics that were closely related to Littlewood’s work. He looked at two results that had been proved by Littlewood conditionally under assumption of the validity of the generalized Riemann hypothesis. These results were about the growth of the values of what are called Dirichlet L-functions L(s,\chi), at the point s=1 as the modulus k of the character \chi increases. Chowla proved one of the results unconditionally using two of his favourite objects: r_{s,k}(n) and class numbers. In later years, he also provided an unconditional proof of Littlewood’s second result.

While reminiscing about her father [8], Chowla’s daughter Paromita wrote about what she must have heard from him about his PhD student days. We learn from her reminiscences that during his Cambridge days, Chowla had developed a close friendship with the famous physicist S. Chandrasekhar. They were house-mates, and continued to correspond for years after. The supportive bond between them is discernible in a letter that Chandrasekhar wrote to Chowla a few years later in October 1933, at which time Chowla held a faculty position at the Andhra University in erstwhile Waltair (now called Visakhapatnam). After sharing the good news of having been elected to the Fellowship at Trinity College, Chandrasekhar writes,

Chowla formed friendships with many other mathematicians, including the celebrated number theorist Harold Davenport, who was also a student of Littlewood. Although they did not collaborate mathematically during his Cambridge days, and wrote their first (and only) paper together nearly thirty years later, Chowla and Davenport maintained a lifelong friendship.

Equipped with a PhD, Chowla returned to India in 1931.

Eagerly expecting a letter from you

Before we follow Chowla’s journey through various colleges and universities in India, it would be worthwhile to learn more about the number theorist S.S. Pillai, with whom he formed a strong friendship and collaboration.

S.S. Pillai, who was to become famous in the mathematical world for his significant contributions to Waring’s problem, was a lecturer at Annamalai University from 1929 to 1941, before moving to Travancore University and University of Calcutta. He had previously worked as a research fellow under the guidance of K. Ananda Rau and R. Vaidyanathaswamy at the University of Madras. We refer the interested reader to [17] for an overview of his mathematical work and life, which was tragically cut short in a plane crash in August, 1950 while he was on his way to the US to attend the International Congress of Mathematicians at Harvard University.

Based on existing records, it is quite probable that the interaction between Pillai and Chowla started through the posing and answering of questions in the JIMS. They were both present at a conference of the Indian Mathematical Society in December, 1928 and are standing next to each other in the group picture. The correspondence between Chowla and Pillai starts soon after. On the 3rd of January, 1929, Chowla writes to him, mentioning an observation of Hardy, that the smallest positive integer equal to a sum of two cubes in three different ways is 175,959,000. In fact,

175959000 = 560^3 + 70^3 = 552^3 + 198^3 = 525^3 + 315^3.He also answers this question posed by Pillai, “Is it true that every prime factor of m! + 1 is congruent to 1\mod\,m?’’, by providing a counterexample. He then asks Pillai a few other questions, and it is interesting to note that they are all about divisors of certain numbers. Chowla concludes the letter with the hope that they will soon begin to have a proper collaboration.

Thus started a trail of frequent letters among them. We describe a few functions and sums that were of interest to them:

For a positive integer n, let

• \sigma_{\theta}(n):=\sum_{d|n} d^{\theta}, where the sum runs over all positive divisors of n, and \theta refers to a real number. For \theta=0, this function turns out to be the number of positive divisors of n, and is also denoted as d(n). We will refer to this class of functions as “divisor functions”.
• The Euler’s totient function is defined as

  \phi(n) = \sum_{1 \leq a \leq n \atop {(a,n) = 1}} 1,that is the number of positive integers less than n which are relatively prime to n.

• Let F(n) be the number of squarefree numbers less than n which are relatively prime to n. By a squarefree number, we mean a number which is not divisible by the square of any prime.

As is the case with a lot of questions in number theory, the above functions are easy to define. An effort to understand how these functions behave and grow often takes us to deep and foundational realms of mathematics, such as the Riemann zeta function. While many of these functions behave in a somewhat irregular manner, their “average orders”

\frac{1}{x}\sum_{n \leq x} f(n)often grow in a manner that can be codified in terms of special values of zeta functions, or other interesting arithmetic objects. In many cases, \sum_{n \leq x} f(n) grows asymptotically like Cx^A, for some A > 0, where C is related to a special zeta value. The study of the “error”

\sum_{n \leq x} f(n) - Cx^Aor “higher moments” of the error,

\int_1^t \left|\sum_{n \leq x} f(n) - Cx^A\right|^k dx,also leads us to beautiful expressions. The behaviour of these moments is linked to important conjectures, which are now well studied.

They inspired Chowla and Pillai as well, and we find several detailed letters exchanged between them, where they systematically discuss these questions for functions f(n) = \sigma_{\theta}(n),\,\phi(n), F(n), r_{s,k}(n).

The two continued to correspond during Chowla’s travels across the continent, and this discussion eventually led to the first of their two joint papers which appeared in the Journal of the London Mathematical Society in the year 1930, titled On the Error Terms in Some Asymptotic Formulae in the Theory of Numbers -I and II [12], [13]. This was the first time that either of them had published with a collaborator. Later, the first part of Chowla’s PhD thesis also contained results inspired by this theme.

The other topics on which they collaborated were the “continued fraction” expansions of numbers of the form \sqrt{R} and the growth of r_{k,k}(n) as n\to\infty. The former has connections to the Brahmagupta-Pell equation

x^2 - Ry^2 = 1.Their last joint paper appeared in 1936, but they continued to correspond until Pillai’s untimely demise in 1950. We further refer the interested reader to the article [16] by B. Sury and R. Thangadurai on the work of Chowla and Pillai, and their correspondence.

The letters from Chowla to Pillai reveal his characteristic enthusiasm, his admiration for Pillai, and how much the correspondence meant to him. Although these letters mostly contain mathematics, we also find references to other matters, such as travel plans, logistical arrangements, academic events and job searches.

For example, in a letter written in January of 1936, Chowla mentions an upcoming job interview in February in Delhi. In July, however, he writes something that would be relatable to most adults:

Although we are not sure which job application is being referred to here, it does seem probable that the position was in Delhi. This makes us wonder how different things could have been if Chowla had obtained this position. Right after expressing his disappointment, Chowla follows up with,

Chowla is referring to Pillai’s celebrated work on Waring’s problem, and indeed, the result that he is referring to did find Pillai a place in history.

Another letter in November 1934 contains two interesting and mysterious questions.

Chowla’s 1940 letter to Pillai on Waring’s problem courtesy: R. Thangadurai.

First, Chowla requests for a proof of a claim made by Pillai that the greatest prime divisor of the number n^2 + 1 is (n^{1/12}), that is, it is less than or equal to C n^{1/12} for an absolute constant C, as n \to \infty. This is an unpublished result, and to date, a manuscript containing the proof seems to be unavailable.

Second, Chowla asks if the winners of the Ramanujan Memorial Prize had been announced. Both Chowla and Pillai would have been contenders for this prize. In that year, the prize went to S. Chandrasekhar, S. Chowla and D.D. Kosambi [19]. From some archival documents related to Pillai, we infer that Pillai received the prize the following year.

The India years

When Chowla returned to India in 1931 after obtaining his PhD, his first position in India was at St. Stephen’s College. Here, he met and married Himani Majumdar. Himani belonged to a progressive Bengali Brahmo family. Her sister Sucheta (Kripalani, post marriage) was actively involved in India’s freedom struggle, and served as the chief minister of Uttar Pradesh from 1963–1967. Chowla’s associates and students remember Himani as an astute, considerate, practical and warm person who was a gracious and caring host when they visited, often staying with the Chowla family, even for long durations sometimes. In a note about his memories of Chowla, Atle Selberg writes [8],

By all accounts, the Chowlas built a happy family life together. Their daughter Paromita, born in 1934, also went on to become a mathematician.

The seven page letter that Chowla wrote to K.S. Krishnan exactly a month before the Indian independence that speaks of his concerns arising out of the imminent partition of India. Vijay Thiruvady

Chowla moved from St. Stephen’s to Banaras Hindu University(BHU), and then to Andhra University in Waltair. The vice chancellor of Andhra University at that time was none other than Sarvepalli Radhakrishnan, who was the second President of India from 1962 to 1967. In these years, Chowla interacted with several people, who are now remembered as distinguished scientists and nation builders. For example, in his BHU years he met Andre Weil, T. Vijayaraghavan (a well known number theorist at the Aligarh Muslim University, and his future collaborator) and D.D. Kosambi (who was at BHU before moving to Aligarh). One luminary with whom Chowla built a steady and lasting correspondence of friendship was the distinguished physicist K.S. Krishnan, who was a former student and collaborator of C.V. Raman. In 1933, Krishnan had joined the Indian Association for the Cultivation of Science in Calcutta as a faculty member. Krishnan was also instrumental in the building of many departments and institutions, including the National Physical Laboratory, where he was appointed its first director in 1947. He maintained correspondence with several scientists, and young scientists found a great friend and mentor in him. Vijay Thiruvady, the grandson of K.S. Krishnan, has carefully maintained several archival documents associated with his grandfather, which he has generously shared with the Bhāvanā team. In this collection lies a series of letters from Chowla, written between 1934 and 1948, some of which are reproduced here.

In these letters, we get a glimpse into the lives and experiences of faculty members at universities in India. In a bunch written between July and October 1934, Chowla gives updates about a serious health situation of a colleague called Bhagavantam, who was being treated for pleurisy. Concerns are expressed if Bhagavantam would recover from the illness. Bhagavantam here is Suri Bhagavantam, a physicist at Andhra University during Chowla’s tenure there. Fortunately, he would indeed recover from the illness, and go on to live a long and brilliant life, serving as a vice-chancellor of Osmania University, director of the Indian Institute of Science, and the director general of DRDO (Defence Research and Development Organization). Another interesting person we hear about in Chowla’s letters is K. Nagabhushanam, his colleague in the mathematics department, who later became the first head of its department of statistics in 1951.

In these years, Chowla continued to publish actively in several areas of interest to him, and stories about his mathematical prowess made their way to school students. The well-known statistician C.R. Rao recalls,[8]

In 1936, Chowla moved to the city of his childhood, Lahore. He joined his alma mater, the Government College of Lahore as the Head of the Department of Mathematics. Here, he taught students such as Faqir Chand Auluck, Ram Prakash Bambah and Abdus Salam.

One of his earliest students was Faqir Chand Auluck, whose early work with Chowla was on the partition function and Waring’s problem. Auluck eventually moved to theoretical and statistical physics, and received his PhD in 1946. Auluck went on to have a stellar career as described in the INSA (Indian National Science Academy) archives⁵, and retired as the Aryabhata Professor of Physics, University of Delhi.

Another student of Chowla who moved to physics was the Nobel laureate, Abdus Salam. As a B.A. student at the college, he got interested in an equation of Ramanujan mentioned by Chowla during a class. In a week’s time, he derived another proof of this equation that was apparently simpler than Ramanujan’s proof. After completing his master’s in Mathematics, he completed the Cambridge Tripos in Mathematics. He obtained his PhD in Theoretical Physics from the Cavendish Laboratory at Cambridge, and went on to win the Nobel Prize in Physics in 1979, jointly with Sheldon Glashow and Steven Weinberg.

Ram Prakash Bambah, a year senior to Abdus Salam, was also taught by Chowla during his undergraduate and postgraduate studies. He joined Chowla as a research scholar in March 1946. Between April ’46 to February ’47, they wrote a total of 15 papers. In an interview with Bhāvanā [3], Bambah (now 97) describes his interaction with Chowla in the following words:

In the mid 1940s, Chowla also got interested in combinatorics. The high-school student from Waltair that we mentioned earlier in this section, C.R. Rao, was now a young researcher at the Indian Statistical Institute, Calcutta. Chowla read a paper by Rao, and sent him a postcard congratulating him on his results. Rao’s mentor, Raj Chandra Bose then invited Chowla to Calcutta in 1945 to discuss some combinatorial problems. This sparked off a new collaboration: Bose, Chowla and Rao wrote several papers together on the solvability of some challenging congruence equations over finite fields. Chowla and Bose also worked together on the construction of affine difference sets.

In 1947, in the aftermath of the partition of India, both Bambah and Chowla had to leave Lahore, which is now part of Pakistan, and with great difficulty, they managed to relocate to India safely along with their families. Bambah had already moved to Delhi in February of that year. He went on to obtain his PhD at Cambridge under the supervision of L.J. Mordell. He had an illustrious career, and was instrumental in creating and building a thriving mathematics department at the Panjab University, Chandigarh. He also served as the vice-chancellor of the university in later years. We refer the interested reader to [3] for his phenomenal mathematical journey, and for very detailed descriptions of his interactions with Chowla.

The Chowla family escaped to Nainital. In July 1947, Chowla wrote a long letter to K.S. Krishnan about his plans. In response to a Punjab government circular, he had indicated a choice to move to East Punjab (now, the state of Punjab in India). However, he was told that he might have to stay for up to six months in Lahore. This was obviously not a wise option, given the prevailing violence in Lahore at the time. In this situation, Chowla applied for a senior fellowship of the National Institute of Sciences in India. He also mentions an application to be included in a scientific deputation by the Government of India to be sent abroad, and requests for Krishnan’s support for both applications. He had also applied for a position at Delhi University the previous year without success. He then mentions strong references obtained from stalwarts like Mordell, Davenport, Littlewood and Hardy. He gives citations of his work by several distinguished number theorists, and while doing so, manages to give an idea of his major contributions to a physicist.

It appears that his applications for positions in India were not successful. After a brief sojourn in Delhi with the family of Mrs. Chowla’s sister, Sucheta Kripalani, the Chowlas moved to the United States in early 1948. Chowla had been offered a temporary membership at the Institute for Advanced Study(IAS) in Princeton. Thus started a new chapter in his life.

“The perpetual ambassador for number theory” (The US years)

The Chowla family moved to the US in early 1948. Chowla received financial support both from the Indian government and the IAS, and entered the US with a visa for a foreign government official. Due to the then prevailing immigration laws, his salary was held in escrow for some time. As a result, the Chowla family had to battle financial difficulties in the early days. They had arrived right in the middle of an extreme winter, and Selberg recalls Himani walking in the snow with thin open-toed sandals in that year. In these early days, they managed through the kindness of strangers. The Chowlas faced their challenges with grace and tolerance, with Chowla’s mathematical acumen supplying the purpose and meaning to go on.

Soon, Chowla immersed himself in the academic atmosphere at the IAS. Atle Selberg, now recognized as one of the most visionary number theorists of the twentieth century, was a visiting member at the IAS at that time. Selberg preferred to work on his own. During their interactions, Chowla made a remark to Selberg about his interest in computing the value of the “quadratic L-function” of the imaginary quadratic field Q(\sqrt{-163}) at the point s = 1/2. Selberg knew a formula related to what is called the Epstein zeta function, which would give the answer to Chowla’s question. They continued the discussion, and also saw applications to results about periods of elliptic functions with complex multiplication. This led to a joint research article. They announced their work in the Proceedings of the National Academy of Sciences of the United States of America in 1949, but the complete article with all the details and proofs appeared much later, in 1967, in the Journal für die Reine und Angewandte Mathematik (Crelle’s Journal). Chowla and Selberg maintained a correspondence for many years after, and also developed a warm friendship. But this was to be their only publication together, and for that matter, Selberg’s only publication with a co-author.

Another interesting collaboration of Chowla that arose around this time was with Nesmith Ankeny. Ankeny was a student of Emil Artin at Princeton University, and later, also a Fellow at the IAS. Chowla and Ankeny met at the Institute. They discussed Chowla’s favourite theme, namely class numbers, and soon announced results about class numbers of cyclotomic fields, as well as a relationship between the class number of imaginary quadratic fields and the distribution of primes in arithmetic progressions. This led to a collaboration with Emil Artin, and together, the three of them proved the famous Ankeny-Artin-Chowla theorem about the class number of real quadratic fields, which appeared in the Annals of Mathematics in 1952. Ankeny and Chowla continued to collaborate over the next two decades. Other number theorists that Chowla developed a connection with, in these years, include Carl Siegel, Paul Turán and Paul Erdõs

Chowla joined the University of Kansas at Lawrence in 1949 as a professor, and stayed there for three years. This period saw the beginning of his collaboration with the phenomenal Paul Erdõs. They wrote two papers in this duration (one of them was in collaboration with Paul Bateman, with whom Chowla also collaborated in later years): these were about the size and distribution of special values of certain Dirichlet L-functions.

Another notable collaboration from these years is that of Chowla and Herbert Ryser, a leading figure in the world of combinatorics. Chowla and Ryser extended a previous result of Richard Bruck and Ryser providing necessary conditions for the existence of symmetric block designs. This result,
called the Bruck-Ryser-Chowla theorem, is an extremely important theorem in combinatorics with useful applications.

In the year 1952, Chowla moved to University of Colorado at Boulder, where he was to remain until 1963. Here, Chowla, along with Burton Jones (also a faculty member there), organized several conferences in number theory called the Boulder Number Theory Meetings. In one such conference, R.C. Bose presented his joint result with E.T. Parker and S.S. Shrikhande, in which they disproved an old conjecture of Euler by showing that if n \geq 10, there always exist mutually orthogonal Latin squares of order n. Chowla, Erdõs and Ernst Straus were in the audience, and were able to use an inequality from Bose and Shrikhande to show the stronger result that if A(n) is the number of mutually orthogonal Latin squares of order n, then A(n) \to \infty.

Chowla’s friendly nature, enthusiasm and an all-encompassing love of number theory charmed and attracted many people, including those who could be classified as “mathematical introverts’’. One such “introvert’’ was the celebrated number theorist L.J. Mordell, who, like Selberg, mostly worked on his own. Chowla and Mordell proved a theorem on the non-vanishing of certain “quadratic” Dirichlet L-functions at the point 1, and provided a short and elegant proof.

Chowla supervised a total of 13 students during his tenure at the University of Colorado at Boulder, including his daughter Paromita. His former PhD student Sanford Segal, in his reminiscences of Chowla, describes his supervision style [8]:

In 1963, Chowla moved to Pennsylvania State University, where he was offered a research professorship. Describing Chowla’s activities at Penn State, George Andrews, who joined Penn State as an assistant professor in 1964, recalls [8],

Chowla’s abundance of ideas and generosity in sharing them attracted and inspired many mathematicians, especially the younger ones. There was a warm human side of this man whose life was totally mathematics—mathematics played the connecting thread, and his human aspects embraced everyone who came in contact with him. It earned him the sobriquet, “a perpetual ambassador for number theory” from one of his students, Philip Leonard. Some of his other students from these days were Paul Hartung, John Friedlander, Mary Cowles and James Huard.

In 1965, Chowla wrote a small book titled The Riemann hypothesis and Hilbert’s tenth problem [14]. His goal was to present a selection of some beautiful “pearls” in number theory. In a conversation with M. Ram Murty in 1980 when they were both at IAS Princeton, Chowla mentioned that he wrote the book in a single night with the intention of stimulating the reader to further study. Although Chowla did not choose the title to suggest any connections between the two problems, connections between them were indeed discovered later.

Chowla stayed on at Penn State until his retirement in 1976. Sadly, Mrs. Chowla passed away in the year 1970, leaving a huge void in his life. After her demise, Chowla started spending more time at IAS, and after his retirement, he again moved to Princeton. Here, he won over some more young collaborators through his enthusiasm, including K. Ramachandra (who went on to play a pivotal role in building the number theory ecosystem in India), Bruce Berndt and Dorian Goldfeld. By asking questions and sharing ideas, he often provided an inroad for others to gain an entry into the subject, or made them aware of fresh directions.

Dorian Goldfeld reminisced later [8] that he and Chowla often talked about quadratic fields and a classical class number problem of Gauss. Goldfeld had not thought about this problem at all before he met Chowla, and Chowla introduced him to the vast literature on this subject. He continued to work on this problem, and Chowla was absolutely delighted when Goldfeld, Gross and Zagier settled it years later.

Some time in 1972, Chowla’s enthusiasm had an unanticipated effect: it brought about a meeting between a number theorist and a physicist, which led to the birth of a revolutionary phase in number theory, namely the interface between random matrix theory and number theory. Hugh Montgomery was a doctoral student of Harold Davenport at Cambridge, and was visiting Selberg in 1972. He was strongly interested in the spacings between the zeros of the zeta function on the critical line. One morning, he was describing some results and a conjecture he had made about these spacings (later known as Montgomery’s pair correlation conjecture) to Selberg in his office. Chowla came into the office at that time, and Selberg requested Montgomery to explain his results to Chowla. Later, in the afternoon, while Montgomery and Chowla were having tea together, Chowla noticed Freeman Dyson at the other end of the room. Chowla immediately wondered if Montgomery had met Dyson: Montgomery said no, and hesitated (quite strongly) to make an acquaintance. But, Chowla kept insisting that they meet. The incident is now best described in the words of Montgomery in a 2022 conference celebrating 50 years of the Dyson-Montgomery meeting [20]:

Had Chowla not brought about this fortuitous meeting between Montgomery and Dyson at just the right time, it is unclear when the connection between the spacings of zeta zeroes and random matrix theory would have been made. Figuring out the connection right at the beginning provided a steady and fruitful direction to this theme, and Chowla was the inadvertent cause.

After a few more productive years at the IAS, Chowla moved from Princeton to Laramie, Wyoming. Here, he continued to collaborate with his former doctoral student Mary Cowles, and her partner John Cowles. Mary Cowles also looked after him in his old age. In 1986, after a breathtakingly productive career spanning 60 years and 350 papers, Chowla published his last paper. He passed away in 1995 at the age of 88.

We leave the reader with a moving image of Chowla’s last days. Sometime in the summer of 1992, Chowla’s former student, John Friedlander arranged to visit Chowla, and spend some time with him. He found Chowla at a nursing home. Friedlander writes [8],

Acknowledgements

I am thankful to C.S. Aravinda for his encouragement and insightful inputs during the preparation of this article, and for sharing important archival documents related to S. Chowla, including his letters to K.S. Krishnan. I am grateful to R. Thangadurai for helpful discussions about the correspondence between S.S. Pillai and S. Chowla, and for sharing letters from S. Chowla to S.S. Pillai. I also thank Siddhi Pathak for sharing important excerpts from The Collected Papers of Sarvadaman Chowla, which, unfortunately, is now out of print and was inaccessible to me. I thank M. Ram Murty for several helpful discussions about the life and work of Chowla, and for his comments on a previous draft of this article. We thank James Huard for his kind help referring us to a picture of the participants at the Sixth Conference of the Indian Mathematical Society in 1928 at Nagpur.\blacksquare

References

• [1] Sarvadaman Chowla, R. Ayoub, Journal of Number Theory, Vol. 11 (1979), 286–301.
• [2] Sarvadaman Chowla (1907-1995), R. Ayoub, J. Huard and K. Williams, Notices Amer. Math. Soc. 45 (1998), no. 5, 594–598.
• [3] From the land of five rivers, Bhāvanā, Vol. 4(1), 17–37, (2020).
• [4] Questions 1346 and 1348, S. Chowla, Journal of the Indian Mathematical Society, Vol. 15 (1924), 167.
• [5] Solution of Question 1252 (Sanjana), S. Audinarayanan, S. Chowla, I. Totadri Iyengar, Journal of the Indian Mathematical Society, Vol. 16 (1925), 54.
• [6] Solution of Question 1252 (Sanjana), S. Chowla, Journal of the Indian Mathematical Society, Vol. 16 (1925), 88.
• [7] Remarks on Question 1348 (Chowla), S. Chowla, Journal of the Indian Mathematical Society, Vol. 18 (1929), 44.
• [8] The collected papers of Sarvadaman Chowla. Vol. I. 1925–1935. Edited by James G. Huard and Kenneth S. Williams. Université de Montréal, Les Publications CRM, Montreal, QC, 1999.
• [9] Some identities in the theory of numbers, S. Chowla, J. Indian. Math. Soc. (Notes and Questions), 18 (1929), 87–88.
• [10] Expressions for the class number of binary quadratic forms, S. Chowla, J. Indian. Math. Soc. 18 (1929), 145–146.
• [11] A property of positive odd integers, S. Chowla, J. Indian. Math. Soc. (Notes and Questions), 18 (1929), 87–88.
• [12] On the Error Terms in some Asymptotic Formulae in the Theory of Numbers (I), S. Chowla and S.S. Pillai, J. London Math. Soc. 5 (1930), no. 2, 95–101.
• [13] On the Error Terms in some Asymptotic Formulae in the Theory of Numbers (II), S. Chowla and S.S. Pillai, J. London Math. Soc. 5 (1930), no. 2, 181–184.
• [14] The Riemann hypothesis and Hilbert’s tenth problem, S. Chowla, Mathematics and its Applications, Vol. 4, Gordon and Breach Science Publishers, New York-London-Paris, 1965.
• [15] Sarvadaman Chowla (1907-1995), J. Huard, The collected papers of Sarvadaman Chowla. Vol. I. 1925–1935, Edited by James G. Huard and Kenneth S. Williams. Université de Montréal, Les Publications CRM, Montreal, QC, 1999, iii–vi.
• [16] S. Chowla and S.S. Pillai: the story of two peerless Indian mathematicians, B. Sury and R. Thangadurai, Resonance volume 17, 855–883 (2012).
• [17] S.S. Pillai, K. Chandrasekharan, Jour. Indian Math. Soc., N. S. Part A. 15 (1951), 1–10.
• [18] The work of Sarvadaman Chowla, M.R. Murty, V.K. Murty and K. Williams, The collected papers of Sarvadaman Chowla. Vol. I. 1925–1935, Edited by James G. Huard and Kenneth S. Williams. Université de Montréal, Les Publications CRM, Montreal, QC, 1999, vii–xxiii.
• [19] Ramanujan Memorial Prize in Mathematics. Nature 135, 28 (1935)
• [20] Opening remarks and history of the math talks – Peter Sarnak, Hugh Montgomery and Jon Keating, 50 Years of Number Theory and Random Matrix Theory Conference, June 2022, IAS Princeton.

Footnotes

1. According to their hosted website https://www.informaticsjournals.com/index.php/jims, the Indian Mathematical Society began publishing “Progress Reports’’ right from 1907, and then the journal from 1908 (the 1908 and 1909 issues of the journal were titled “The Journal of the Indian Mathematical Club’’). From 1910 onward, it is published as its current title The Journal of Indian Mathematical Society. ↩
2. Sanjana often posed interesting questions that caught the interest of his contemporaries: one of Ramanujan’s earliest published articles in 1912 was in response to a question by him. ↩
3. This is a special case, for n=3, of the famous “last” theorem of Fermat. This case had been previously proved by Leonhard Euler in 1770. ↩
4. Mathematische Zeitschrift. ↩
5. https://www.insaindia.res.in/detail.php?id=N50-0032 ↩