Scaling the Everest

Introduction

The life and work of Radhanath Sikdar (1813–1870) is, by and large, unknown to people outside a small scientific community of scholars. So is the debate over his contributions to the identification of the highest mountain peak in the world—Mount Everest. It is claimed that the peak which goes by the name of Sir George Everest, the former Surveyor General of the Great Trigonometrical Survey of India (GTSI), was actually mathematically scaled by Sikdar, an employee of the Survey Office in Calcutta. The true nature of Sikdar’s contributions to the computing process that clinched the debate over which was the highest peak in the world has been a matter of contestation for close to a century. Although scholarly work on the man and his achievements are very few, there have been enthusiasts who have campaigned emphatically for giving Sikdar his due credit. On the other hand, British scholars, officers and geographers are divided in their opinion as to who should receive the actual credit for having calculated the height of Mount Everest. There is, however, complete agreement among all concerned that the tagging of the name of Everest (1790–1866) to the peak was an act of respect to the man who headed the survey office for years although he had already retired by the time the discovery of the peak and its height were made and announced to the public. Indeed, Everest did not have anything to do with the initial calculations or sightings of the peak.

This essay does not attempt to shed any additional light on the debate on who determined the height of Mount Everest as scholars have already commented at length on the matter. Instead, it tries to foreground the significance of the mathematical contributions made by Sikdar, and take the readers through the main points in the debate on the exact role played by him.

Early life

Sikdar was a member of the famous Young Bengal group, also known as the Derozians, or student associates of the Hindu College¹ teacher Henry Louis Vivian Derozio (1809–1831). Sikdar studied at the Hindu College for approximately seven years. His father, Tituram Sikdar, had fallen on hard times and wanted young Sikdar to take up a vocation as soon as possible. The eldest of four children, Sikdar had shown early indications of mathematical aptitude. His academic inclinations were taken into account and he joined the Hindu College to receive higher education under the illustrious faculty of the institution. He was taught by John Tytler, who was a professor of mathematics at Hindu College, in addition to being a surgeon and a member of the Calcutta Medical Society. He used his proficiency in languages such as Arabic, Hindustani and Sanskrit to translate books of European science and mathematics into these languages, and even made Newton’s Principia Mathematica a common textbook in his mathematics classes. The Hindu College in those days had a comprehensive curriculum which emphasized both the liberal arts as well as scientific enquiry and education. Of particular note is that apart from being exposed to Euclid’s Elements, the curriculum also discussed topics like Kepler’s Problems, Windhouse’s Analytical Geometry, and Windhouse’s Astronomy.

Sikdar was a contemporary of Rajnarain Bysack and Peary Chand Mitra aka Tekchand Thakur, the latter being the author of the first prose piece in simple Bengali, Alaler Gharer Dulal. At the college, Sikdar’s knack for mathematics was identified early and honed carefully by the tutorship of two eminent teachers, Tytler and D.~Ross. Sikdar was one of the two pupils in those days who had read the Principia Mathematica. His talents were acknowledged by his teachers and peers alike. When Everest came looking for bright young Indians possessing a working knowledge of mathematics and physics to help with his new technique of measuring distances (called the Colby Bar System), Sikdar’s name was recommended promptly by none other than his teacher, Tytler. Thus, even before he could complete his degree course at Hindu College, Sikdar was hired to the post of “Computer” in the Survey Office in 1831.

Sikdar had received sufficient encouragement and inspiration in his Hindu College days from his fellow Derozians, who had created a social uproar in their attempts to establish the merits of scientific rationality and empirical knowledge, and the demerits of irrational beliefs and religious rigidities (see [11]). Bred in that tradition, Sikdar continued with his mathematical and astronomical education through his own efforts and under the able guidance of officers such as Everest and his successor, Andrew Scott Waugh. He was transferred for a while to the Dehradun headquarters of the GTSI. Later, in 1849, he was promoted to the post of “Chief Computer’’ and brought back to the Calcutta office. Sikdar was considered to be a mathematical genius by his mentor Everest. Several interesting correspondences provide glimpses into the prestige Sikdar enjoyed among his colleagues and superiors. In 1832, Everest remarked about Sikdar (see [9] pp.[15–16]):

This was high praise indeed, considering the fact that the Indians were regarded as objects of scientific enquiry rather than subjects of their own fields of enquiry (see [10] and pp[153–178]).

To his existing job in the Survey office was later added the additional charge of Superintendent in the Meteorological Observatory at Calcutta. In that capacity, Sikdar had to grapple with weather forecasts and related calculations which became crucial for a wide array of functions, including travel by water. Sikdar was the first Indian superintendent to be appointed to the Meteorological Department.

Among Sikdar’s principal contributions, mention may be made of his discovery of new theorems, his discovery of how to calculate distance and height after making due allowances for refraction, his simplification and standardization of mathematical tables used for trigonometrical survey operations, his discovery of a formula for reducing barometrical observation to a standard 32 degrees Fahrenheit, a compilation of formulae for converting chronometer times to sidereal times, his successful operation of the blue lights using Everest’s “ray tracing method”, and so on. Sikdar is said to have been responsible for initiating the process of compilation of hourly Meteorological observations and its publication. Some of his views on geodetic surveying² may be found in A Manual of Surveying for India, published in 1851. In fact, Sikdar substantially contributed to writing some of the chapters in this compendium. His contribution to the compilation of the book was lauded in the following passage in the preface to the work (see [3], [pp 9–10]):

The man and his mathematics

Sikdar’s contributions must be assessed for their scientific merit, and in this section, we attempt a brief evaluation of some of his works. Sikdar was appreciated for his mathematical acumen both by Everest and by many of his contemporaries, including Waugh. In 1838, Everest commented about Sikdar in the following way (see [8], [pp 340–341]):

In 1864, Sikdar was made an honorary member of the Society of Natural History, Bavaria, which was a huge achievement in those days. On this occasion, the Hindu Patriot wrote on 25 April 1864 (see [5], [p. 59]):

In his time, Sikdar was the only Indian to publish a paper on geometry in a reputed science journal. The article, in the form of a short note, was called, “Drawing a common tangent”. It was published in Gleanings in Science, Vol. III, October 1831. Sikdar was 18 years of age at the time and a student at the Hindu College. The article narrated the construction of a common tangent to two circles. M.C.~Chaki mentions (see [4]) that Sikdar’s paper was one of the ten papers in geometry published during 1800–1850 in India. His construction was innovative because of the clever use of the notion of similar triangles in the proof, which was probably new at that time. We provide an illustration of this proof below:

Let G and H be the circles with centres A and B respectively. Draw the line segment AB and choose a point L on the line so that AL : LB = AM : BN. Draw the line segment LD which is tangent to the circle G at the point D. Now connect A and D and draw the line segment through B parallel to AD. Let this segment meet the extended line segment LD at the point C. Now to show that CD is a common tangent to both circles, it is enough to show that C is a point on the circumference of the circle H and the angle BCL is a right angle. The triangles ADL and BCL are similar by the Angle-Angle-Angle postulate and hence AL : LB = AD : BC. This implies that AM : BN = AD : BC, which proves that C is a point on the circumference of the circle H. Now, the angle ADL, which is a right angle, is the same as the angle BCL and hence the angle BCL is also a right angle. This proves that the above construction produces the common tangent CD.

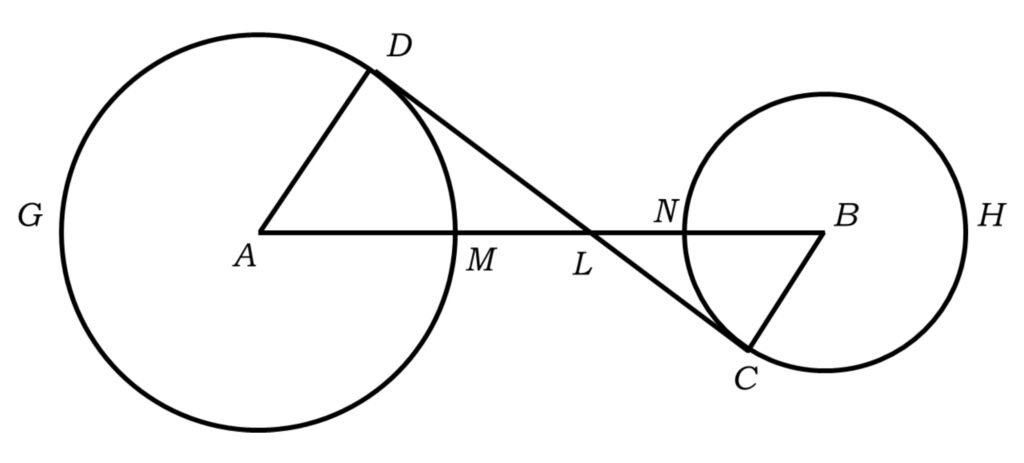
On finding the meridian

A meridian is an imaginary arc of longitude on the surface of the earth connecting the north pole and the south pole. Sikdar gave a “very simple, and sufficiently correct” (in his own words) method for finding the meridian for ordinary purposes (see [13]). The time and altitude of the pole star were noted using a certain transit instrument, and was taken as the approximate meridian. The calculation of the deviation from the true meridian is in terms of the horary angle,³ and zenith and polar distances of the Polaris. He proved by the sine formula that the deviation calculated by his formula would be within two or three seconds of the true value. The accompanying image of his original publication gives a fuller picture of this discussion.

The theorem of minimum squares

Sikdar is believed to be the first to apply the “Method of Minimum Squares’’ to the streamlining of large amounts of conflicting and raw observational data. He wrote two long papers in 1851, explaining the method of the minimum squares or the least squares. The least square method is the process of finding a line of best fit (or the regression line) for any set of points. In this method, the sum of the squares of residual distances of the points from the best-fitted line is minimized. In his correspondences with Waugh, Sikdar wrote extensively on “Computation Methods’’ and on “Computation of Heights’’. These correspondences may be found at the National Archives of India, New Delhi. In 1852, Sikdar wrote an important piece on computational methods in “Dehra Dhoon Trilaterals made agreeably to the Theorem of Minimum Squares’’.

On barometric corrections

Sikdar calculated the corrections in the barometric heights of a barometer, taken at different temperatures, considering the dilation of the mercury and the dilation of the brass cable attached to the barometer. To incorporate the two corrections he made use of the formula

C = B\frac{(t-32^{\circ})m-(t-62^{\circ})b}{1+(t-32^{\circ})}, where C= Sum of the two corrections, B= Observed height of the Barometer, t= observed temperature of the mercury, and of the brass scale which are assumed to be equal, m=0.000100 Expansion of mercury for 1^{\circ} of Faht., b=0.0000106 Expansion of brass for 1^{\circ} of Faht., 32^{\circ}= Standard temperature of mercury, and 62^{\circ}= Standard temperature of brass.

While employing the above formula, Sikdar writes (see [14], [pp. 359–332]) that “it is the same as that which Col. Boileau makes use of… referring his readers to p. 67 of Galbraith’s tables…’’ and further adds “Col. Boileau gives no demonstration of the process. Galbraith may have done so, but as the works of the latter are not within my reach, I have been necessitated to satisfy myself of the truth of the formula…’’. He then provides his justification to go about the meticulous computations involved.

On the `ray trace method’

The `ray trace method’ was introduced by Everest while surveying the Jamuna region of the Delhi zone in 1835. This was the method using `blue lights’ (for their clear visibility even from distances of 50–60 miles) to determine the direction between two points, visible from one to the other, if the view is unobstructed. Everest came up with the innovative idea of burning blue lights behind an iron screen with an aperture of 3–3.5 inches in diameter, so that the flame is not blown aside by strong wind. The centre of the aperture was duly positioned over the station so that the flame was visible through the aperture.

Suppose B, C, D and E are the points to be observed by an observer at A. For points B and C to be observed, the method uses a point of reference R and calculates the angles BAR and CAR by positioning a lamp or a flag at R and by firing blue lights (at regular intervals) at points B and C. The angle BAC is then given by the difference between the angles BAR and CAR.

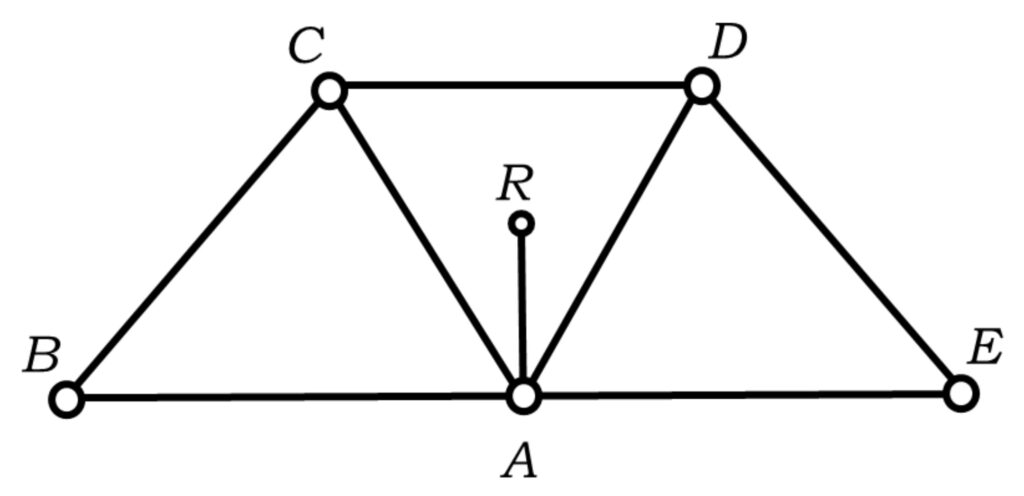
Similarly, the angle CAD is given by the sum of the angles CAR and DAR, which can be calculated by similar techniques. The calculation was done for points on the whole arc and several cautions were observed to minimize errors in the observations. Sikdar mastered the technique so well that he wrote an entire chapter (XV) titled `On the Ray Trace System and the Great Trigonometrical Survey of India’ in A Manual of Surveying for India (1851), compiled by Smyth & Thuillier, pp. 372–83) where he described the method with examples.

Other contributions of Sikdar

Among numerous important innovations of Sikdar, two deserve special mention: (i) Developing a technique for conversion of chronometer times to sidereal times, and (ii) introducing the system of hourly observations to compile the first-ever scientifically recorded set of meteorological data that led to the first-ever work on the climatology of an Indian city (Kolkata, the then capital of British India). This endeavour, which started in December 1852, took 24 long years and was considered the finest piece of knowledge of the climate of Calcutta. Sikdar’s innovative abilities and command over the subject made him an asset to the Survey of India till 1862, the year he retired.

The Mount Everest controversy

The controversy surrounding his calculation of the height of Mount Everest took intriguing turns over the years. The issue did not come to light when Waugh presented the case for Mount Everest to the Royal Geographic Society. The matter had not yet surfaced when the discovery was first announced at a meeting of the Asiatic Society of Bengal in 1856. Later, in 1904, S.G.~Burrard, the then Surveyor General, claimed that Peak XV was identified by Sikdar as the highest peak in the region. This claim was published in an article titled “The Story of a Long Controversy”, in the scientific journal Nature on 10 November 1904. The claim was later refuted by others, but vehemently supported by a few. There is no knowing at this point where the truth lies. However, both Ashish Lahiri and Shankar Kumar Nath (see [1] and [9]) have argued forcefully that Sikdar was responsible for processing the various calculations of distance and height of mountain peaks in that region that had been noted by several officers trying to record the height from multiple directions and that it was Sikdar’s calculation that clinched the debate in favour of Peak XV, later named as Mount Everest. These scholars have alleged a deliberate campaign to obliterate the name and contributions of one of colonial India’s earliest mathematical brains with the intention of denying Indians their due credit. With the help of some correspondences between Sikdar and Waugh, the Surveyor General, and other officers at the Dehradun office of the GTSI, Ashish Lahiri has shown that Sikdar was constantly examining the data generated by field officers as part of the North East Longitudinal Series which contained observations pertaining to the snow peaks, between 1849, when Sikdar arrived back in Calcutta, to the early 1850s. Lahiri has argued that there was quite a bit of confusion created by the huge mass of data generated and that this computational confusion was sorted out by Sikdar who applied the method of the minimum squares to the process. Lahiri has provided a list of these correspondences in his book. Lahiri observes (see [1]):

Whatever be his actual contribution to the final calculation of the height of the peak, there is no doubt that Sikdar was a man to reckon with in his days. His superiors needed his mathematical acumen as much as his sincerity. Letters and correspondences with him, and concerning him, testify to this fact. What sowed the seeds of belief in a controversy to obliterate the name of Sikdar from the annals of survey operations is the fact that soon after Sikdar’s death, his name as one of the principal contributors was removed from the preface to the book A Manual of Surveying for India. Sikdar had after all been given full charge of the computing section in Calcutta, and it is hardly likely that his assistance and opinion were not sought in the final stages leading up to the announcement. Given the manner in which Col.~Thuillier went about the process of erasing Sikdar’s name from the manual, it seems more than a little likely that the obfuscation was a posthumous process carried out at the behest of the Surveyor General to get even with a defiant “native”, whose legendary skills in computing and intrepid nature had become something of an irritant to his colonial superiors. Thuillier, one of the authors of the volume, had warmly acknowledged Sikdar’s contribution in a previous edition but had fallen foul of Sikdar a few years before the latter’s death.

Although initially he had a high opinion of Sikdar, Thuillier’s impressions perhaps changed later, especially when Sikdar criticized him on one occasion. Thuillier was then the Deputy Surveyor General under Waugh. Sikdar, as the Superintendent of the Calcutta Observatory, had challenged Thuillier on the less than smooth functioning of the `time ball signalling’ system used for weather forecasts. Thuillier was higher than Sikdar in the official hierarchy, and the matter was reported to Waugh, who asked for an explanation and later apology from Sikdar. In his Science and the Raj, Deepak Kumar points out that under Thuillier’s leadership, when the latter was made the Surveyor General, the GTSI was transformed into an organisation that focussed primarily on cadastral surveys⁴ or revenue surveys which had a direct bearing on the government’s revenues. When the GTSI was set up in 1818, it was meant to supervise all kinds of surveys, whether trigonometrical, topographical or cadastral. After Waugh’s retirement, the office of the Surveyor General was separated from that of the superintendence of the Trigonometrical Survey, and Thullier was made the Surveyor General. In that capacity, between 1861 and 1878, Thuillier almost exclusively carried out only revenue surveys which came to be called “Cadastral Surveys”. At the same time, it is also true that there was always a great deal of overlap between the activities of both the offices. Therefore, Thuillier’s preoccupation with revenue surveys indicates his strong investment in the colonial enterprise of revenue expansion. In 1878, all three branches of the erstwhile GTSI were again amalgamated. The Surveyor General was placed in charge of the overall administration, while a Deputy Surveyor General, General Col.~John Macdonald, was placed in charge of the revenue surveys. It was the latter who accused Thuillier of deliberately and maliciously removing Sikdar’s name from the list of contributors in the newly published edition of A Manual of Surveying for India. Macdonald wrote an article in The Friend of India on 24 June 1876 to this effect (see [9], [p. 109]):

When Macdonald was penalised by the Government of India for accusing his superior, many English language newspapers such as the Pioneer, Statesman and Englishman supported Macdonald and criticized the removal of Sikdar’s name from the manual. The Friend of India also published a statement made by a retired officer of the Survey office who observed that he was “ashamed for those who have seen fit to exclude his name from the present edition…”. The latter claimed that Sikdar must be acknowledged (see [9] , [p. 111]) also for “the advice so generally afforded on all subjects connected with his own judgement”.

Sikdar: The Crusader

Sikdar was not merely a mathematician with a keen intellect. He was a versatile person known for his fearless nature. This often drew him into controversies and confrontations involving his white superiors. He was known to be a man who did not tolerate exploitation of subordinates. He was once fined for seizing the luggage of District Magistrate Vansittart, who had asked Sikdar’s men in the Survey office to act as coolies. The incident was reported in the bi-lingual weekly newspaper The Bengal Spectator on 17 May 1843. He also protested (see [1], [ pp. 54–55]) the low level of pay for Indian Survey personnel and the lack of a systematic policy for leave and promotion for the latter. Sikdar’s nationalist instincts were quite strong in those days when organized politics was yet to make its appearance in India. His vociferous protests, both verbal and written, against oppression and callousness, which must have hampered his career prospects a good deal, provide insights into his sense of justice in general and his love for his countrymen in particular.

Sikdar also took a great deal of interest in social matters. He was a supporter of Ishwar Chandra Vidyasagar’s widow remarriage movement. He himself abhorred child marriage and had refused to marry a girl of eight who had been selected as his bride by his family. He was keen that Bengali prose must be written in a simplified manner so as to be comprehensible to the women of the household. With that purpose he helped co-edit a monthly magazine for women called Masik Patrika along with his famous contemporary, Peary Chand Mitra. In this regard, Shibnath Shastri notes (see [12], [p. 205]) in his Ramtanu Lahiri o Tatkalin Banga Samaj that Sikdar used to say, “Of what use is that Bangla language if it is not comprehensible to the womenfolk’’? James Long’s A Descriptive Catalogue of Bengali Works published in 1855, describes the Masik Patrika in the following terms (see [9], [p. 52]):

Sikdar was concerned that the Bengali diet was not adequate for hard work and for building a strong physique. He recommended a nutritious diet for the Bengalis including meat, in order to help build muscles. He himself was very particular about his own diet and is said to have followed a fitness regimen which included practising boxing and the like. He is said to have indulged in boxing bouts with Englishmen in his college days.

Shankar Nath has cited the testimony of J.C.~Marshman to show that Sikdar had converted to Christianity at some point of time in his life. The reasons behind this switch are not known. However, as a rebellious Derozian, his beliefs and views must have brought him into confrontation with orthodox practices. His opposition to child marriage and his support for widow remarriage are well known. His unorthodox views must have led him to live the way he believed in. He had settled down in the French colony of Chandan Nagar after coming back to Calcutta in 1849. Sikdar took early retirement from the Survey Department. He retired in 1862, when he was only 49 years of age. The reason officially cited by him was ill health. However, it is quite possible that he was actually disillusioned with the treatment of natives in colonial establishments. He passed away in his house on 17 May 1870. His burial site could not be identified with certainty. No attempt has been made either to preserve the house or his memories in any significant manner. But for the significant efforts made by a few scholars and enthusiasts, Sikdar’s contributions to the GTSI would have been lost to posterity forever.

Quite a few obituaries seem to have been penned at his death. Being covered by the press was not unusual for Sikdar in his lifetime. His name had come up in the press on several occasions. In 1852, when he applied for an additional position, that of the Superintendent of the Calcutta Meteorological Observatory, Allen’s India Mail wrote (see [9] , [p. 13]):

In 1864, two years after his retirement from the GTSI, Sikdar visited Dehradun once again. The science magazine Hills wrote on this occasion (see [9], [p. 66]):

Sikdar was remembered by his peers, and his achievements were celebrated both during his lifetime and after his death. His anglicized habits did not make him very popular with sections of the Bengali Bhadralok, while his intrepid nature prevented him from becoming a universal favourite among the British officials. Indian newspapers like Somprakash were not kind to him in their obituaries. Yet, his mathematical knowledge, keen intellect and overall erudition were widely acknowledged at a time when Western science was busy putting down its colonial roots which implied that the “native’’ had to remain as an underling to the “superior’’ skills and “knowledge’’ of the colonial masters. In The Great Arc (see [6]), John Keay remarks, “As well as being the first Indian of rank in the employ of the Great Trigonometrical Survey and its undoubted mathematical star, Sickdhar too would be credited with Himalayan discoveries’’. Keay observes (see [6] and Lahiri1[]) that the Survey’s historian, Reginald Phillimore pointed out that Waugh, the Surveyor General, had asked his Chief Computer in Calcutta, the “Bengali genius whose arithmetical wizardry had so impressed Everest”, “to revise the form of computing geographical positions of snow peaks at distances of over 100 miles’’. What could be better proof of Sikdar’s involvement in the computational process than this, although Phillimore dismisses the claim that Sikdar was instrumental in calculating the height of the peak. Keay himself was dismissive of the claims made on behalf of Sikdar. Yet, so overwhelming was the evidence in favour of the claim that he was involved in some manner with the process, as the official in charge of minimizing error in the data, that Keay’s conclusion in this regard, was quite diffident. Keay noted (see [6]), “But it is quite probable that Sickdhar’s computations provided the first clear proof of XV’s superiority’’. This perhaps is one of the closest approximations of the role that Sikdar played in the entire exercise of scaling the height of the highest mountain peak in the world. It seems very likely that Sikdar helped streamline the bewildering variety of raw data generated from the multiple sightings from multiple directions by multiple field operators, and helped refine the calculation by making an allowance for the refraction factor. In these and many other ways, his assistance continued to be used throughout the final stages of the calculation leading to the identification of Peak XV as the highest peak in the world.

Acknowledgement: The author is grateful to Dr Indranath Sengupta for the his valuable assistance in interpreting the mathematical components in the essay.\blacksquare

References

• [1] Ashish Lahiri, Radhanath Sikdar and Colonial Science: Indian Surveys an Uncharted Terrain (Sahitya Samsad: Kolkata, 2016).
• [2] Ashish Lahiri, Radhanath Sikdar and the Final Phase of Measuring Peak XV, Indian Journal of History of Science, 51.2.1 (2016) 280-288
• [3] Captain R. Smyth and H.L. Thuillier, A Manual of Surveying for India (Calcutta, 1851).
• [4] M.C. Chaki, History of Development of Geometry in India During the 19th-20th century (Calcutta Mathematical Society: Kolkata, 1987).
• [5] Deepak Dan, ed., Radhnath Sikdarer Atmakatha o Mulyayan (Patralekha: Kolkata, 2016).
• [6] John Keay, The Great Arc: The Dramatic Tale of How India was Mapped and Everest was Named (Harper Collins: UK, 2001).
• [7] Deepak Kumar, Science and the Raj: A Study of British India, Oxford University Press, New Delhi, 1995.
• [8] R.H. Phillimore, Historical Records of the Survey of India, vol. III (Dehra Dun,1954).
• [9] Shankar Kumar Nath, Radhanath Sikdar: Toththyer Aloy (Chirayata Prakashan: Kolkata, 2012).
• [10] Gyan Prakash, “Science `Gone native’ in Colonial India’’, Representations, No. 40, Special Issue: Seeing Science (Autumn, 1992).
• [11] Susobhan Sarkar, On the Bengal Renaissance (Papyurus: Calcutta, 1979).
• [12] Shibnath Shastri, Ramtanu Lahiri O Tatkalin Banga Samaj, (Reprint, Punashcha: Calcutta, 2007).
• [13] Radhanath Sikdar, Method of finding the Meridian; Gleanings in Science, Vol. III, October 1831).
• [14] Radhanath Sikdar, Journal of the Asiatic Society of Bengal, volume 21, 1852.

Footnotes

1. Editor’s note: Later this college was called Presidency College and now it is known as Presidency University. ↩
2. A survey of large areas which takes into account the curvature of the earth. ↩
3. The apparent time by the sun, or the sidereal time of the moon, or planets, or stars, from the meridian. ↩
4. A survey focussed on establishing land/property boundaries. ↩