Writing Small Omegas

Alberto Cogliati’s book offers a magnificent historical panorama on Élie Cartan’s work on group theory, in particular on Lie groups. It also contains valuable information on important aspects of Cartan’s life, such as his training period and the mathematicians with whom he interacted. In reviewing the contents of this book, I will consider other existing books and survey articles on Cartan’s work–-in particular a report made by Poincaré–-and also make a few remarks on Cartan as a geometer.

The Title

The title of the book under review needs some explanation, and commenting on it and making a few digressions will give the reader some preliminary indications as to the content of the book.

The expression “continuous group” in the title refers to what we call today a “topological group”. This is a manifold equipped with a group structure, whose operations are continuous with respect to the topology induced by the manifold structure. In practice, the manifold and the group operations are assumed to be differentiable.¹ The emphasis is on the group structure rather than on the manifold. Roughly speaking, in the finite-dimensional case, such a manifold corresponds to what we call today a Lie group. A Lie group acts on itself but also on other spaces, and such a group action is often seen as a family of transformations parametrized by a manifold.² One should note however that this description, in a strictly historical perspective, should be taken with care, since in Sophus Lie’s times the notion of a manifold with structure (topological, differentiable, analytic, algebraic, etc.) as we understand it today–-that is, defined by an atlas with coordinate charts preserving some given structure–-was still non-existent.³ Thus, in that context, talking about “dimension,” and saying that a “continuous group” is finite or infinite, was based on a certain parameter count (like Riemann did in his work on the moduli space of Riemann surfaces).

The year 1894 in the title is the year in which Élie Cartan defended his doctoral dissertation. The title of his dissertation was “On the structure of finite and continuous transformation groups” [5]. The jury consisted of Émile Picard, Charles Hermite and Paul Appell. In this work, Cartan completed the classification of complex finite-dimensional semisimple Lie algebras. The classification was essentially done by Wilhelm Killing before Cartan, but Killing’s proofs contained gaps. Regarding this matter, let us quote Cartan from his Notice on his own work, written in 1939 [[12], p. 19], talking about his dissertation:⁴ “In a series of important memoirs, Killing had made significant progress in the theory [of finite and continuous groups], and in particular, he had determined all simple groups with complex parameters. But his proofs contained many gaps and some parts were imprecise. In my thesis (1894), I committed myself to put some order and rigour everywhere. I also obtained, independently of Killing, new results.” In particular, Cartan showed the existence of exceptional simple Lie groups and Lie algebras over the complex field, a fact that Killing had mentioned without proof. Cartan further developed the results of his dissertation in several papers. In particular, in 1914, he determined all simple groups with real parameters, a result which turned out to be useful for his later work in Riemannian geometry.

Lie’s theory remained a major component in Cartan’s work for the rest of his career

Cartan’s thesis was not his first published work. In the year preceding his thesis defence, he published two Comptes-Rendus notes titled “On the structure of simple, finite and continuous groups” and “On the structure of finite and continuous groups” [2], [3], in which he announced complete proofs of fundamental results of Killing. This work later became a part of his thesis. In the year preceding his thesis, he published a paper in German titled “The structure of finite transformation groups” [4], in which he indicated how one can make Killing’s results on simple groups rigorous.

By the time Cartan defended his thesis, Lie’s work was well known in France. In the year 1892 or 1893,⁵ Lie made a visit to Paris during which he discussed with Cartan.⁶ Lie had made previous visits to Paris, one in 1870, another one in 1882, and probably met other French mathematicians. His work was known to (and highly praised by) Gaston Darboux, Émile Picard, Henri Poincaré and others. Furthermore, during the last quarter of the nineteenth century, several French students from France were sent to study mathematics in Leipzig, where Lie was teaching, and German students were also sent to France, despite the Franco–Prussian war which had taken place a few years before, in 1870. One consequence of this interaction was that Cartan had a profound knowledge of the theory developed by Lie, acquired not only from the published work of the latter, but also through his personal contacts, discussing with the young French mathematicians who spent some time in Germany and the German mathematicians who visited France. Lie’s theory remained a major component in Cartan’s work for the rest of his career.

It is probably time to say a few words on the work of Sophus Lie. One of Lie’s important contributions from the point of view of continuous groups was motivated by his approach to partial differential equations and differential systems. His idea was that the important point in the study of differential equations is the search for symmetries of their solutions. Here, one should make a parallel between this idea and that of Galois’ approach to the problem of solvability of polynomial equations through the study of symmetries of their roots.⁷ This is based on the fact that the coefficients of a polynomial may be expressed in terms of symmetric functions of its roots⁸ and that a permutation of these roots does not change the coefficients of the polynomial. This is where group theory appears in the question of the solvability of polynomial equations, and this was also the origin of Lie’s idea of studying a differential equation by associating to it a group, namely, the group of transformations of the space of solutions. When this group depends on a finite number of parameters, the integration of the system of partial differential equations is reduced to the integration of a series of auxiliary systems that depend only on the group considered. Thus, Lie, motivated by his work on the integration of systems of partial differential equations, gave a classification of groups as integrable and non-integrable. This also led to Galois-type theories for differential equations which became part of a general theory known as differential Galois theory. The ideas originating in Lie’s work were developed later by Émile Picard, Ernest Vessiot and Jules Drach, among others. They are discussed in Appendices A and B of Cogliati’s book.

The year ending the period that is mentioned in the title of Cogliati’s book, namely, 1926, was chosen by the author because, according to him, this year marks a break in the historical development of the theory of Lie groups, with the emergence of new (global) topological considerations, after the publication of Hermann Weyl’s series of papers on representations of Lie groups, which constituted a turn in Cartan’s approach to the subject.⁹

The “Writing Small Omegas” in the title refers to the following episode. In a letter to Henri Cartan written by André Weil on 15 June 1984, the latter asks: “Didn’t you tell me yourself that, during your childhood, doing math meant for you drawing untiringly small omegas?” The “omegas” that are referred to here are the Greek letters \Omega (in the uppercase)¹⁰ and \omega (in the lowercase) that are often used to designate differential forms. For instance, \[\Omega= \sum A_{i_{1}i_{2}… i_{p}}dx_{i_{1}}dx_{i_{2}}… dx_{i_{p}}\] denotes an exterior differential form on an n-dimensional homogeneous space, where the sum is taken over all combinations of order p of the indices 1,…, n of the coordinates x_1,…,x_n. The equation \[ (\omega^i)’= \frac{1}{2} \sum_{j,k}c_{jk}^i\omega^j\omega^k \] is a version of the so-called Maurer–Cartan equations, where \omega^1,…, \omega^n are invariant exterior differential forms of degree one on an n-dimensional Lie group, \omega^j\omega^k the Grassmann–Cartan product of the two forms \omega^j and \omega^k, and c_{jk}^i the structure constants of the group. (The formulae are extracted from [10].) At the same time, these formulae illustrate the “debauch of indices” in the literature on differential geometry for which Cartan expressed his dislike in the preface of his book Lectures on the Geometry of Riemann Surfaces [8]. He writes there: “I have almost always used the analytic apparatus imposed by the coordinate system which gives the linear element, which is assumed to be given, of the space to be studied. This required the notions of absolute differential calculus, which I strived to present, while extracting as much as possible its essential geometric element and always keeping its closest contact with Euclidean geometry. The distinguished services that were offered–-and that still will be offered–-by the absolute differential calculus of Ricci and Levi-Civita should not prevent us from avoiding computations that are too exclusively formal, where the debauch of indices hide a geometric reality which is often very simple. It is this reality that I have always tried to highlight.” This is confirmed by Shiing-Shen Chern and Claude Chevalley who write in their review of Cartan’s work [[14], p. 244]: “Although [Cartan] himself never refrained from computations, he did not hide his distaste for the computational work on differential geometry which was very fashionable and much of which was of little geometrical interest.”

The fact that the young Henri Cartan was watching his father relentlessly write these omegas is an indication of the importance of exterior differential calculus and differential systems in Cartan’s approach to the theory of continuous groups, which is one of the main topics treated in Cogliati’s book.

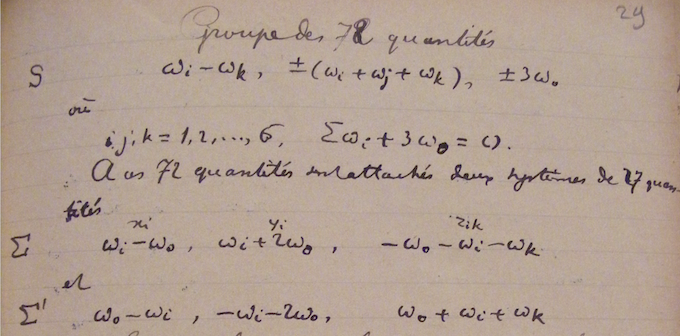
Reports and Surveys on Élie Cartan’s Work

Interestingly, several analyses of Élie Cartan’s work done by pre-eminent mathematicians are available. To name a few, Poincaré wrote in 1912 a report titled “Rapport sur les travaux de M. Élie Cartan” (see [17]); Hermann Weyl published a paper in 1938 titled “Cartan on groups and differential geometry” [19]; Chern and Chevalley, in 1952, published an article titled “Élie Cartan and his mathematical work” [14]; J.H.C. Whitehead, in the same year, published an obituary article titled “Élie Joseph Cartan, 1869–1951” [21]. I would also like to cite a report by Élie Cartan on his own work [12] and several other surveys on his work that he wrote on various occasions. I mention in particular his ICM article “The role of group theory in the evolution of modern geometry” [9], his survey “Group theory and geometry” [7]. There are others too. One may also include in this list the various talks delivered by Émile Picard–-who had been Cartan’s teacher–-and other mathematicians at a scientific jubilee celebration that was held in his honour in 1939 [[11], p. 19]. All these reports and surveys constitute an invaluable collection of documents for a person striving to understand Cartan’s ideas and their place in the history of mathematics.

We already mentioned the book on Cartan titled Élie Cartan (1861–1951) published in 1993 by the American Mathematical Society [1], written by M.A. Akivis and B.A. Rosenfeld, two pre-eminent geometers with substantial experience in the mathematics involved. Finally, let us mention the book by T. Hawkins, Emergence of the Theory of Lie Groups: An Essay in the History of Mathematics 1869–1926, published in 2000 [15].

Poincaré considered that any mathematical notion is a living being, and as such, it has matter and form

Having at our disposal geometrico-historical reports on a mathematical subject written by mathematicians–-and not only historians–-is extremely important for the history of our field, because only the former can have a true feeling of the originality and the profoundness of the work reported on.

Around Poincaré’s Report

Poincaré’s report [17] was written in 1912, at a key moment in Élie Cartan’s career. The latter, who was 43, was applying for a position of professor at the Faculté des Sciences de Paris, and Poincaré wrote his report in support of that application. Cartan had moved to the capital three years before and was already teaching at the Faculty of Sciences there, as “Ma\^itre de Conférences”, a level below that of “Professeur”. He had obtained his doctorate at the same place in 1894, and in the meanwhile, he had held positions at the Universities of Montpellier (1894–1896), Lyon (1896–1903) and Nancy (1903–1909). In Nancy, he had already been promoted to Professeur, but he lost this status when he moved to Paris. His sons Henri (the future mathematician) and Jean (the future musician) were born during his stay in Nancy in 1904 and 1906 respectively. From his years spent in the “Province”,¹¹ Cartan writes the following [[11], p. 54]: “I keep the best memories of the fifteen years that I spent in the Province, first in Montpellier, then in Lyon and Nancy. These were years of calm meditation, and my duly meditated works of that period contain the seeds of everything I did later.”

Cartan’s 1912 application was successful, and in the same year, he was appointed professor (without chair) at the Faculté des Sciences de Paris. From 1924 to 1940, he held the Chaire de géométrie supérieure position there, as the successor of Claude Guichard (1918–1924) who himself was the successor of Gaston Darboux (1881–1918).

Group theory is, so to say, the whole of mathematics, stripped of its matter and reduced to its pure form

The relatively old age at which Cartan was appointed professor in Paris may be explained by the fact that the subject he was working on was not very fashionable in France at that time. Indeed, the first two or three decades of the twentieth century were times when Émile Picard, Jacques Hadamard, Arnaud Denjoy, Émile Borel, René Baire, Henri Lebesgue and several other pre-eminent French mathematicians were mainly interested in questions related to function theory, particularly to functions of a complex variable, trying to generalise important results known for polynomials to the class of meromorphic functions, and opening up the way to what was called later “value distribution theory” or “Nevanlinna theory”. There was also a strong interest in the newly developed set theory initiated by Georg Cantor. In fact, set theory and function theory were related: set theory, with its pseudo-logical apparatus, gave the impression of putting the theory of functions on firm ground. Thus, mathematicians tried to classify functions in terms of set-theoretic properties and limit operations. An example of a newly introduced object is a “Baire function”, obtained from continuous functions by a transfinite iteration of the operation of taking simple limits. First and second category Baire sets were introduced, and so on.

Poincaré disliked that kind of mathematics. In his book Science et méthode [16] published in 1908, he writes: “Logic sometimes generates monsters. The last half-century saw the emergence of a horde of bizarre functions whose endeavour seems to be that of having the least possible resemblance with the honest functions that are useful. No more continuity, or continuity but no derivative, etc.[…] In the old days, when a new function was invented, it had some practical aim; today, we invent them intentionally in order to destroy our father’s reasonings, and this is all we can get from them.”

Cartan had a balanced approach to mathematics, between thinking in algebraic terms and thinking geometrically

Poincaré welcomed Élie Cartan’s work since it was centred on group theory, a field which he considered to be at the heart of mathematics. In the conclusion of his report on Cartan [17], he writes: “We can see that the problems studied by Mr. Cartan are among the most important, the most abstract and the most general that mathematicians deal with. As we said earlier, group theory is, so to say, the whole of mathematics, stripped of its matter and reduced to its pure form.”

Poincaré was a geometer, maybe the supreme model of a geometer. His emphasis on group theory is explained at the beginning of his report on Cartan, and it would be beneficial to spend some time on that.

Let us first recall that group theory is generally acknowledged to be a nineteenth-century invention made by Galois. In that sense, the concept of a group was relatively new at the time where Poincaré wrote his report. Very soon, Poincaré identified group theory with the soul of mathematics. To use his own imagery, Poincaré considered that any mathematical notion is a living being, and as such, it has matter and form. This form is group theory. Together with this distinction between matter and form in mathematics, Poincaré considered that group theory is the connecting element between a variety of mathematical notions. It is possible, he says, to give the same name to mathematical objects that share the same form, even if their underlying matter is different. He formulates this as follows: “Which entity embodies the fact of sharing the same form when matter is different? This question stems from the fact that any mathematical theory is, ultimately, the study of properties of a group of operations, that is, of a system formed by certain fundamental operations and all the combinations that one can make out of them.” Matter, according to him, is “accidental”. He writes: “If we strip the mathematical theory from everything that appears to be accidental, that is, of its matter, then what remains is only the essential, that is, the form. And this form, which constitutes in some sense the solid skeleton of the theory, will be the group structure.”

Élie Cartan agreed with Poincaré’s assertion that group theory was the essence of his own work. In his Notice, written twenty years after Poincaré’s report, he states: “Almost all of my scientific works are organized around group theory.” Commenting on this sentence, he writes that even if the notion of group was “officially” introduced by Galois in his work on the solutions of algebraic equations, “as Poincaré noted, mathematicians were involved in group theory since a long time, and even before Euclid, without being aware of it, since elementary geometry is nothing other than a certain group.” [[10], p. 15] Cartan and Poincaré, like Klein in his Erlangen program, were referring to the fact that a geometry may be characterized by its group of motions (the isometry group, if the geometry is a metric geometry); Euclidean geometry, for instance, becomes in this sense the study of figures that are invariant by the group of Euclidean motions.

Debating, from the historico-philosophical point of view, the statement that Euclidean geometry can be considered as the study of a certain group would put us on shaky ground; in particular, in such a discussion, one has to take into account the Aristotelian principle¹² saying that motion should not appear in the axioms and the proofs of geometry because, this notion belongs to physics and not to mathematics. It is for this reason that Euclid’s Elements do not include motion (or symmetry) in their axioms, statements and proofs. This is important to recall, because some people wonder why Euclid did not use symmetry in the proofs of his propositions. If considerations of motion were allowed, several proofs in the Elements would become much simpler and Euclid was undoubtedly aware of that. This Aristotelian belief, which is certainly a remnant of the Platonic view that mathematical beings are immutable and should not admit motion, had a huge influence on Euclid’s commentators since the Greek period, and it led to a debate which continued with the Arabs of the Middle Ages. All this tells us, in any case, that the statement that group theory existed in Euclidean geometry has to be taken with a lot of care. It was David Hilbert who, in the nineteenth century, officialized the introduction of motion (with various names: congruence, symmetry, isometry, etc.) as an integral part of the axioms of geometry, but this introduction was the result of a very long process that took more than 2000 years to materialize.

Poincaré’s report was written at a key moment in Élie Cartan’s career

It is also interesting to note that Cartan declares in his Notice that not only mathematics, but also physics may be identified with group theory, and that Poincaré, Einstein and others were aware of this fact. For instance, classical mechanics can be seen as comprising a set of laws invariant under the Galilean group: classical electromagnetism or special relativity being governed by the Lorentz group, and so on.

In his report on Cartan, Poincaré proposes a division of groups into four main categories (disregarding, as he says, certain “strange” or “mixed” groups):

1. Discontinuous finite groups, which Poincaré also calls Galois groups: These are the groups we simply call finite groups today. They include permutation groups, the groups that appear in solutions of algebraic equations, etc.
2. Discontinuous infinite groups: These are the groups with properly discontinuous actions on some geometric spaces. They are generally countable. They include Fuchsian groups and Kleinian groups, and those which appear in the theory of elliptic functions and automorphic forms, etc.
3. Continuous finite groups: The word “finite” refers here to the fact that these groups are described by a finite set of parameters. In modern terminology, these are the finite-dimensional Lie groups. Examples are the transformation groups of the classical geometries: Euclidean, hyperbolic, projective, etc.
4. Continuous infinite groups: Poincaré writes that these groups are “much more complex, much more rebellious to a geometer’s efforts. They are naturally connected with the theory of partial differential equations.” Today, they are usually called “infinite-dimensional Lie pseudo-groups”. They appear in Cartan’s theory of partial differential equations. Concerning these groups, Cartan writes in his Notice [[12], p. 20]: “My works on the structure of continuous infinite groups, which are spread between 1903 and 1908, are absolutely personal to me. The only thing they owe to the works of S. Lie on the subject is the very notion of infinite group.”

At the time Poincaré wrote his report, Cartan made important progress on groups of type (1), (3) and (4). Poincaré’s personal work is mostly connected to groups of type (2). Klein worked on groups of type (1) and (2).

Poincaré’s report was published in 1921, in Acta Mathematica, several years after his death.

A Quick Overview of the Book

Cogliati’s book is divided into 6 chapters and 3 appendices.

In the first chapter titled “Lie on the Backstage”, Cogliati reports on the birth of the theory that Lie called “finite continuous groups of transformations”. He surveys the foundations of this theory, and states the three so-called fundamental theorems of Lie, the third theorem being the main result that is key to the classification of finite continuous groups.

After a brief historical account of the life of Élie Cartan, from his childhood up to the year in which he defended his thesis, including a description of the relations between Lie and the Parisian milieu during the last two decades of the nineteenth century, the second chapter gives an overview of Cartan’s doctoral dissertation. At the same time, it provides the reader with an account of Lie’s theory of continuous groups, of Killing’s structural theory and of the theory of integrable groups. In his thesis, Cartan developed the theory of semisimple and simple groups, providing a rigorous foundation to the work of Killing and completing the classification of simple groups initiated by the latter. Cartan also made an important breakthrough in the theory of non-semisimple groups.

It was David Hilbert who officialized the introduction of motion as an integral part of the axioms of geometry

A good introduction to the history of infinite continuous groups constitutes the third chapter. These are groups defined in terms of infinitesimal transformations. They originate in Lie’s work in the 1880s, in particular, his classification of infinite transformation groups in two variables and his theory of differential invariants. The historical point of view adopted in the book gives an informative account of Lie’s motivations, his difficult relationship with Klein, his collaboration with Engel and his connections with his French and Italian colleagues. The chapter also contains interesting information on the work of Ernest Vessiot, who left for a one-year study in Germany, after his agrégation¹³ in 1887, and who defended his thesis in Paris in 1892. This work, together with those of Arthur Tresse and Jules Drach, was partly the result of the intense activity that took place in Paris towards the end of the nineteenth century, as part of their attempts to understand Lie theory and its developments by Killing.

The fourth and fifth chapters are crucial for understanding the nature of Cartan’s work. They cover the period he spent outside Paris, during 1894–1909, working in relative isolation and developing his own tools, especially those that are at the basis of what later came to be known as the Cartan–Kähler calculus and those he used later in his work in differential geometry. Worthy of mention here is Cartan’s exterior differential calculus and his integration theory of these systems.

Cogliati reviews the work of Cartan during the period 1902–1909, on the structure of infinite continuous groups and his re-interpretation of Lie’s equivalence theory in the fifth chapter. He argues that Cartan’s approach to this topic is characterized by a sharp departure, as far as the content, technical tools and perspective are concerned, from the works of his predecessors: Lie, Engel, Vessiot and others. Cogliati claims that Cartan’s emphasis was no longer on the problem of classification of infinite continuous groups, but on the development of a new structural theory of such groups centred on the notion of isomorphisms. He also argues that in the aforementioned period, the problem of classifying infinite groups, although important in itself, was placed in the background and not considered to be a central problem.

The sixth chapter, titled “Cartan as a Geometer”, deals with the period 1909–1926 when Cartan was working in Paris and his research interests gradually shifted to geometry. This period marks the phase when continuous groups started to be regarded as manifolds, and the theory of Lie groups became a part of differential geometry. Because of this transition to geometry, the author thinks that the work of Cartan was later acknowledged as one of the most important mathematical developments in the twentieth century. He explains the particular emergence of the so-called Cartan–Maurer forms, and of Cartan’s generalization of the notion of space, and he explains the way Cartan arrived at the method of moving frames via the theory of continuous groups. This method is a generalization of Darboux’s method of moving frames in Euclidean geometry to a much more general setting. Cogliati also discusses the influence of the emergence of general relativity on this work of Cartan. This chapter includes information on Cartan’s collaboration with the mathematician Jan Arnoldus Schouten, who contributed to the development of tensor and Ricci calculus. The author alludes to the highly important work of Charles Ehresmann which came later. The latter was certainly Élie Cartan’s most gifted student and the best continuator of his work.

Appendices A and B contain further historical notes on the birth of Cartan’s group theory. Here, the author also talks about the Picard–Vessiot theory and the work of Jules Drach. The latter, born in 1871 in Sainte-Marie-aux-Mines (Alsace) in a family of humble farmers, was strongly influenced by Lie’s work, and he set up the goal of developing a Galois theory of differential equations. His work deserves to be better known. The book under review provides a welcome piece of information on this work, reporting particularly on an interesting dispute between Vessiot and Drach. Appendix C consists of a historical introduction to Clifford’s parallelism, in relation with Chapter 6.

The information contained in Cogliati’s book on the life of Élie Cartan and his work, and the mathematicians who had an influence on him, make a truly harmonious ensemble. The only complaint I have is that the book contains at some places unnecessarily long mathematical sections which do not add much to the development and which a mathematician would usually skip; they may well have been abridged or replaced by a few sentences giving the essential ideas.

Cartan as a Geometer

Élie Cartan had a balanced approach to mathematics, between thinking in algebraic terms and thinking geometrically. The geometrical character of his work is more apparent in the second phase of his career (after 1910). Among the geometric theories that we owe him, special mention must be made of the theory of symmetric spaces. These are Riemannian manifolds where, in a neighborhood of each point, the geodesic reflection around that point is an isometry; two of the illustrative examples are the Euclidean plane and the unit sphere in three-dimensional space. Cartan found a complete classification of symmetric spaces, with a decomposition of each such space into irreducible local factors, these factors being related by pairs having nonnegative and nonpositive curvature, respectively. He introduced the notion of rank of a symmetric space, as the maximal dimension of flat totally geodesic submanifolds. (For example, having rank one means that the maximal flat totally geodesic manifold is a geodesic curve, and hence has either positive curvature or negative curvature.) He also studied the global behaviour of geodesics in simply connected symmetric spaces.

Cartan also developed the theory of Finsler spaces (manifolds equipped with metrics that generalize Riemannian metrics, defined by infinitesimal norms, called Minkowski norms, whose unit balls are not necessarily ellipsoids).¹⁴

One may also talk about Cartan’s geometrical works related to special relativity and general relativity, his theory of spinors and his attempts to create a unified field theory which led him to his theory of generalized spaces in which, from a purely geometrical point of view, the notion of infinitesimal transformation of a Lie group and Darboux’s method of moving frames found natural applications.

Chern and Chevalley, in their report on Cartan’s work [[14], p. 218], emphasize the fact that a fair recognition in France of this work occurred only in 1936, due to the influence of André Weil who suggested that Élie Cartan’s work should be the central theme of the seminar organized by Gaston Julia. In the same article, they write that the true value of Cartan’s work in geometry took an even longer time to be acknowledged. In support of their claim, they quote a 1938 review of one of his books by Hermann Weyl who writes [20]: “All of the author’s books, the present one not excepted, are highly stimulating, full of original viewpoints, and profuse in interesting geometric details. […] Nevertheless, I must admit that I found the book, like most of Cartan’s papers, hard reading.”

I would like to end this review by pointing out a few of these “interesting geometric details” whose true importance was recognized much later. They are contained in Cartan’s 1928 book, Lectures on the Geometry of Riemann Spaces [8]. They are the basis of what was called later the theory of Cartan–Hadamard manifolds.

Cartan declares that not only mathematics, but also physics may be identified with group theory

In Note III of this book, Cartan proves that in each homotopy class of paths joining two points in a complete Riemannian manifold of nonpositive curvature, there exists a unique geodesic (a result which is a special case of the so-called Cartan–Hadamard theorem, saying that in such a manifold, the exponential map at every point is a diffeomorphism). He also gives a comparison formula for the divergence of geodesics in such manifolds which is expressed today as a comparison formula for geodesic triangles. This formula says that for a geodesic triangle ABC in a Cartan–Hadamard manifold with corresponding side lengths a,b,c, we have \[c^2\geq a^2+b^2-2abc \cos C.\] He also proves the existence of a centre of gravity for any compact set in a nonpositively curved Riemannian manifold. These facts became part of the foundations of the field of metric geometry, and in particular of the theory of metric spaces of nonpositive curvature developed by H. Busemann and A.D. Alexandrov. One has to mention the formidable revival of this field by Gromov.\blacksquare

References

• [1] M.A. Akivis and B.A. Rosenfeld. 1993. Élie Cartan (1861–1951), Translations of Mathematical Monographs, 123. American Mathematical Society, Providence, RI
• [2] É. Cartan. 1893. “Sur la structure des groupes simples finis et continus’’. C. R. Acad. Sci. Paris. 116: 784–786
• [3] É. Cartan. 1893. “Sur la structure des groupes finis et continus”. C. R. Acad. Sci. Paris. 116 962–964
• [4] É. Cartan. 1893. “Úber die einfachen Transformationsgruppen”. Mitteilungen Leipzig Univ., p. 395–420
• [5] É. Cartan. 1894. “Sur la structure des groupes de transformations finis et continus”. Volume 826 de Thèses présentées a la Faculté des Sciences de Paris pour obtenir le grade de docteur ès sciences mathématiques, Faculté des Sciences (Paris), Èd. Nony
• [6] É. Cartan. “La théorie des groupes et les recherches récentes de géométrie différentielle”. Enseign. Math. 24 (1925): 1–8; Proc. Internat. Math. Congress Toronto 1 (1928): 85–94
• [7] É. Cartan. 1927. “La théorie des groupes et la géométrie”. Enseign. Math. 26: 200–225
• [8] É. Cartan. 1928. “Leçons sur la géométrie des espaces de Riemann”. Gauthier-Villars, Paris
• [9] É. Cartan. 1937. “Le rôle de la théorie des groupes de Lie dans l’évolution de la géométrie

moderne”. Proceedings of the ICM, Oslo, 1936, Vol. I, A.W. Brøggers Boktrykkeri A/S, Oslo, p. 92–103

• [10] É. Cartan. 1939. Selecta: Jubilé scientifique de M. Élie Cartan. Paris, Gauthier-Villars
• [11] É. Cartan. 1939. Jubilé scientifique de M. Élie Cartan. Paris, Gauthier-Villars
• [12] É. Cartan. 1939. Notice sur les travaux scientifiques de M. Élie Cartan. Gauthier-Villars, Paris. Reprinted in [10].
• [13] Correspondance entre Henri Cartan et André Weil (1928–1991), ed. M. Audin. Société Mathématique de France, 2011
• [14] S.-S. Chern and C. Chevalley. 1952. “Élie Cartan and His Mathematical Work”. Bull. Amer. Math. Soc. 58: 217–250
• [15] T. Hawkins. 2000. Emergence of the Theory of Lie Groups: An Essay in the History of Mathematics 1869–1926. Springer-Verlag
• [16] H. Poincaré. 1908. Science et méthode. Flammarion, Paris
• [17] H. Poincaré. 1921. “Rapport sur les travaux de M. Élie Cartan”. Acta Mathematica. 38: 137–145
• [18] A. Stubhaug. 2002. The Mathematician Sophus Lie, Springer Verlag
• [19] H. Weyl. 1938. “Cartan on Groups and Differential Geometry”. Bull. Amer. Math. Soc. 44: 598–601
• [20] H. Weyl. 1938. Review of La Théorie des Groupes Finis et Continus et la Géométrie Différentielle traitÈes par la Méthode du Repère Mobile, by Élie Cartan, Bull. Amer. Math. Soc. 44: 598–601
• [21] J.H.C. Whitehead. 1952. Élie Joseph Cartan, 1869–1951. Obituary, Notices Royal. Soc. London 8: 71–95
• [22] F. Lê. 2017. “Ce n’est pas un des résultats les moins intéressants et les moins inattendus de cette étude…”. Images des Mathématiques. 15 Jan 2017.

Footnotes

1. Editor’s Note: As illustrative simple-minded examples, one can cite the real line \mathbb{R}.or the Euclidean $n$-space \mathbb{R}^n with their additive group structures, or the unit circle S^1 in the complex plane \mathbb{C} with its multiplicative group structure. ↩
2. Editor’s Note: As an example of this, one can consider the Euclidean space \mathbb{R}^4 acting on itself by addition; \mathbb{R}^4 can also be identified with the set M(2,\mathbb{R}) of 2\times2 matrices with real entries, which acts on \mathbb{R}^2 by matrix multiplication. In the latter instance, the manifold parametrizing the action on \mathbb{R}^2 is the group M(2,\mathbb{R}). ↩
3. Editor’s Note: See endnotes to Cogliati’s article for some of this discussion. ↩
4. In this article, the translations from French are ours. ↩
5. There is a disagreement regarding the date and the length of this visit. According to Cartan’s recollections, the date is 1892 and it lasted six months (see the text extracted from Cartan’s estate at the Academy of Sciences quoted on p. 17 by the author of the book under review). According to Stubhaug [18], the visit was in 1893 and lasted only three weeks. ↩
6. Akivis and Rosenfeld report in [[1], p. 6] that the main purpose of Lie’s visit was precisely to meet Cartan, a piece of information that was given to them by the latter’s son, Henri. ↩
7. Editor’s Note: See Robert P. Langlands. “Is there Beauty in Mathematical Theories? Part II. Bhāvanā. 3(2). Apr 2019. ↩
8. Editor’s Note: As an example of a symmetric function, one can take the polynomial x_1^2+x_2^2-x_1x_2 in two variables in which interchanging the two variables is not going to change the polynomial; in other words, this polynomial is a symmetric function of the two variables. ↩
9. Little is said about this in the book under review. ↩
10. I don’t think the term “small omegas” refer only to the lowercase. ↩
11. This is the word that the French use for any place outside Paris. ↩
12. Cf. Aristotle’s Physics 193b33 and other passages. (Editor’s note: 193b33 refers to page 193, line 33 of the second column of the Prussian Academy of Sciences edition.) ↩
13. Editor’s Note: The agrégation is a competitive examination in France for teaching in the school system. ↩
14. Incidentally, the term “Finsler space” was introduced by Cartan. ↩