Mathematics in India

Vedic and Sūtra Literature as Source Materials

Ancient India had a strong tradition in mathematics. This has been presented to modern scholarship with much wealth of detail by dedicated historians of mathematics like Bibhutibhusan Datta (1888–1958). Unfortunately, there is still a lack of awareness about the mathematical accomplishments in Indian civilization among students in India. In this series of articles, we plan to record a few glimpses of what is currently known about mathematics in India from the Vedic Age till the sixteenth century of the Common Era. We shall also discuss the major primary source materials from which historians of mathematics have described the developments in Indian mathematics during various phases of its history. For convenience, the major source materials can be roughly divided into three broad categories: (i) Vedic literature, (ii) Sūtra literature (including the Vedā\dot{n}ga), (iii) Post-Vedic literature.

In this section, we shall describe the nature of the Vedic and Sūtra literature as source materials for our knowledge of mathematical attainments during the Vedic and Sūtra periods. We shall discuss, in the next section, examples of the knowledge of geometry during the Vedic period. In the next instalment, we shall discuss the accomplishments in other branches of mathematics during the Vedic and Sūtra periods. Lastly, we shall delve into the mathematics of the post-Vedic period.

Vedic literature

Indian traditions recall the attainment of an advanced state of civilization—in terms of wisdom, power and social organization—during a period of remote antiquity. This was an era when both the inner and outer life of civilized societies had been guided by the spiritual impulse, when wisdom sprung from mystic insights. All that was celebrated in later periods was believed in India to have their ultimate roots in that golden era. In the subsequent phases of ancient Indian civilization, there had been repeated efforts to climb back to the lofty heights once attained in that luminous dawn.

While the great mystics of that illustrious past could have belonged to any ancient country, some of their original doctrines and insights appear to have been preserved in considerable detail, often in symbolic language, in the earliest layers of the Vedic literature; while some of their technical knowledge is recorded in the later Vedā\dot{n}ga literature. Even the earliest layers of Vedic literature represent only the closing stages of that great period. However, it is from the Vedic literature that glimpses of the atmosphere of that golden era can be envisaged. Below is a broad outline of Vedic literature.

The four Vedas as is well known are: Ṛgveda, Sāmaveda, Yajurveda and Atharvaveda. Each of them has four subdivisions: Sa\dot{m}hitā, Brāhmaṇa, Āraṇyaka and Upaniṣad. The Sa\dot{m}hitās contain the Mantras; the Brāhmaṇas mainly contain commentaries on the Mantras, descriptions of sacrificial rites and narrations of symbolic legends; the Āraṇyakas are for the recluses who meditated in forests; and the Upaniṣads are spirituo-philosophical treatises.

Though the above is the formal classification, in popular terminology (for instance in the oft-used expression “Vedas and Upanishads”), the word “Vedas” usually refer to the Sa\dot{m}hitā (Mantras) and Brāhmaṇa (ritual) treatises. The oldest extant treatise in the world is the Ṛgveda-Sa\dot{m}hitā. Again, the name Ṛgveda usually refers to the Ṛgveda-Sa\dot{m}hitā.

Mathematical evidence in the Vedas: Direct

Though the Vedas are not meant to be technical texts on “mathematics” and “science” (as is usually understood today), there is direct evidence in the Sa\dot{m}hitā and Brāhmaṇa texts, of certain mathematical attainments in the Vedic period. The foremost among them is the Vedic number-vocabulary from the Ṛgveda-Sa\dot{m}hitā onwards, which survives in the Sanskrit language as we know it today. This number-vocabulary is in the (verbal) decimal system and contains seeds of algebraic mathematics.¹ However, the algebraic significance of the decimal nomenclature in Vedic literature has not received due attention in the history of mathematics.

Apart from the number-vocabulary, the Sa\dot{m}hitā and the Brāhmaṇa literature also provide examples of fundamental arithmetic operations, often involving large numbers. Not being texts in mathematics, the explicit methods for performing the fundamental operations are not to be found in Vedic literature; they are described in post-Vedic treatises on mathematics. These methods are based on decimal notation and are, in essence, the same as the modern methods with minor variations.

Accurate computations involving large numbers indicate that well-developed computational algorithms must have already been in vogue during the Vedic period. From the fact that numbers were orally represented in the (polynomial-like) verbal decimal system, one can surmise that the methods of fundamental operations during the Vedic period would not have been too different in spirit from the methods which we see in post-Vedic texts, which themselves are, in essence, modern methods.

Thus, from the number-vocabulary and the examples of fundamental arithmetic operations in Vedic literature, one may justifiably argue that the roots of modern arithmetic go back to at least the Vedic period. We shall discuss the number-vocabulary and its significance and the examples of arithmetic operations in the next instalment.

Mathematical evidence in the Vedas: Indirect

A major example of indirect evidence of geometric and other mathematical attainments during the early Vedic period is the description in the Sa\dot{m}hitā and Brāhmaṇa texts of intricately designed fire-altars called citi, vedi or agni, constructed out of burnt bricks, and mud mortar. The complexity in the design of these brick-altars arises from their rich symbolic significance. For instance, the śyenacit (falcon altar) is a symbolic representation of the aspiration of the spiritual seeker soaring upward. The k̄urmacit (tortoise altar) and the rathacakracit (chariot-wheel altar) are two other examples of Vedic fire-altars with intricate designs.

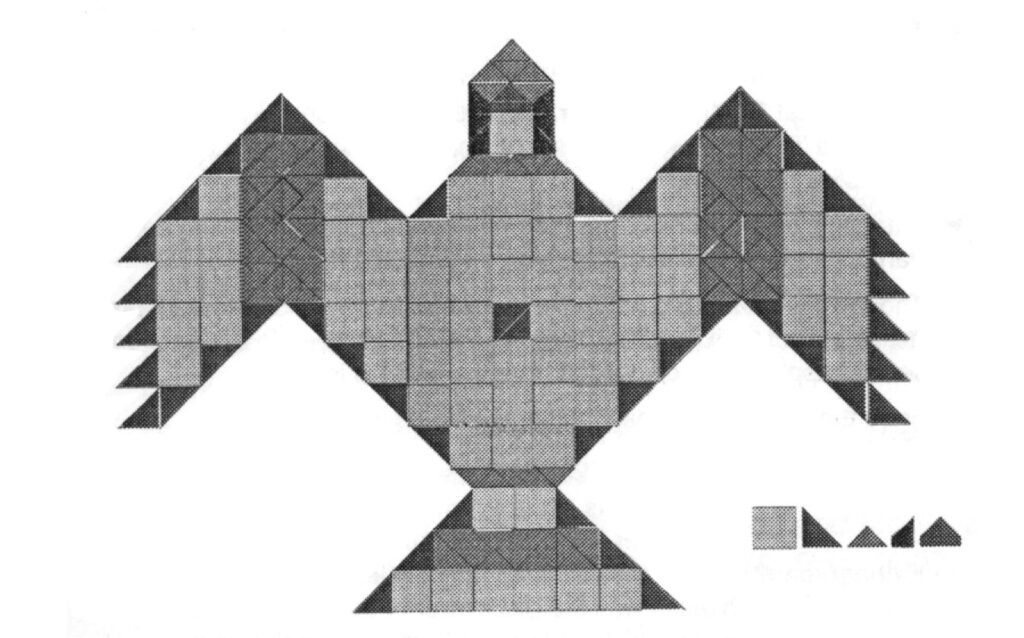
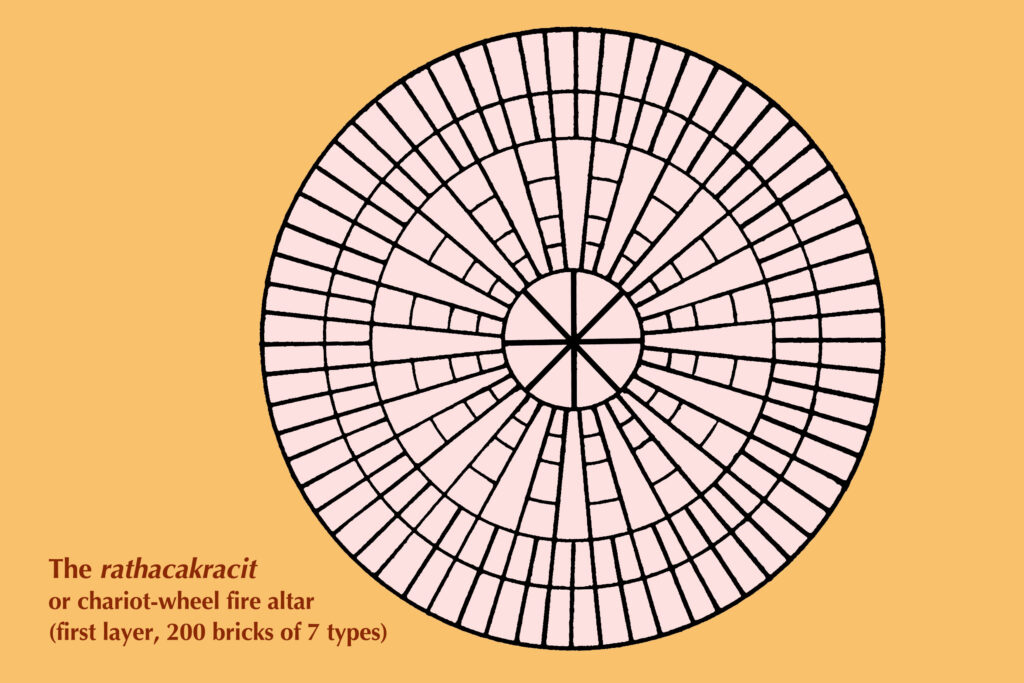
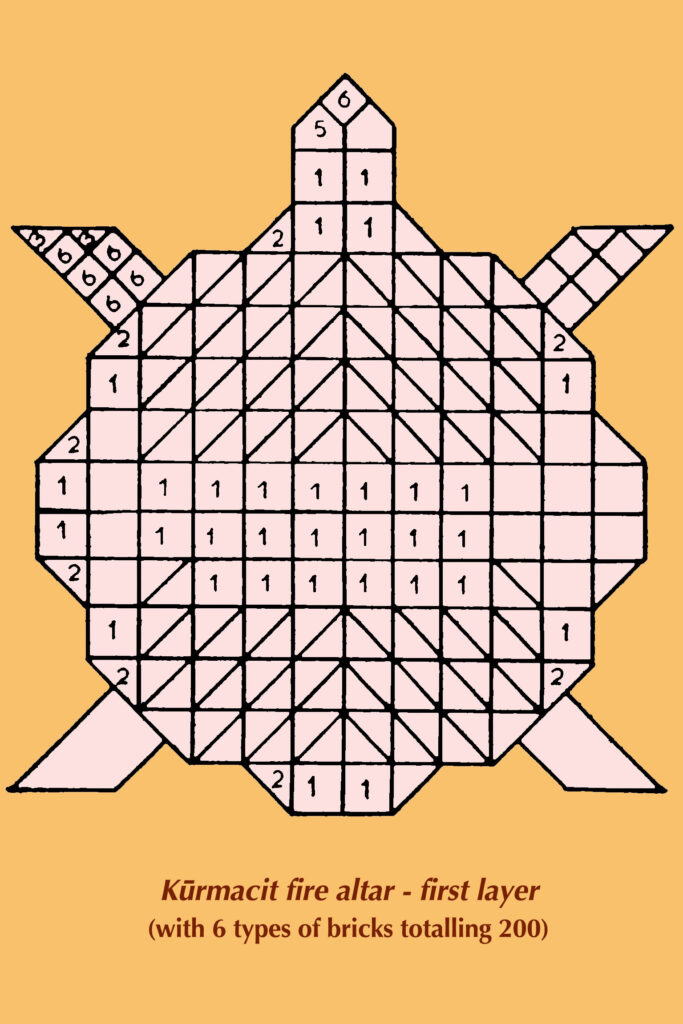
The Vedic tradition demanded that the constructions of these inspired symbolic fire-altars be executed with perfection—with little room for error. This requirement of precise constructions of the involved designs was met through remarkably sophisticated geometric innovations.

The principles of geometry involved in the constructions of the Vedic fire-altars are explicitly stated in the Śulba-Sūtras belonging to the Vedā\dot{n}ga period (also referred to as the late Vedic period). But the constructions of Vedic altars (which require knowledge of Śulba geometry) are described in detail in the Śatapatha Brāhmaṇa; some are mentioned in the still earlier Taittirīya Sa\dot{m}hitā of the Yajurveda. The descriptions of the altars in these older treatises are the same as those found in the later Śulba-Sūtras. In fact, the Śulba authors emphasise that they are merely stating facts already known to the authors of the Brāhmaṇas and Sa\dot{m}hitās. Even the Ṛgveda Sa\dot{m}hitā, the oldest layer of the extant Vedic literature, mentions the sacrificial fire-altars (though without explicit descriptions as in the Śatapatha Brāhmaṇa or the Taittirīya Sa\dot{m}hitā).

Thus the major Śulba results and constructions in geometry, a few of which will be mentioned in the next section, were known and applied during the early Vedic period. Thus the roots of Indian geometry can be traced to at least this Vedic period, at least to the Taittirīya Sa\dot{m}hitā and the Śatapatha Brāhmaṇa.

Dating of Vedic literature

From the above discussions, one can see that three Vedic texts are particularly important for the history of mathematics: the Ṛgveda Sa\dot{m}hitā, Taittirīya Sa\dot{m}hitā and the Śatapatha Brāhmaṇa. While there is consensus on the relative chronology of these three Vedic texts, there is a wide divergence among even serious scholars regarding their dates. According to the historians subscribing to the framework of a theory of Aryan invasion or migration around 1500 BCE, the Ṛgveda Sa\dot{m}hitā was composed sometime during 1500–1200 BCE, the Taittirīya Sa\dot{m}hitā around 1000 BCE and the Śatapatha Brāhmaṇa around 800 BCE. However, according to B. Datta, Ṛgveda Sa\dot{m}hitā was composed well before 3000 BCE, Taittirīya Sa\dot{m}hitā around 3000 BCE and the Śatapatha Brāhmaṇa around 2000 BCE. A date around 3000 BCE for the early Vedic period is also being suggested by researchers on early Indian astronomy. The precise dates of these texts will not affect our appreciation of the significance and depth of the mathematical knowledge of the Vedic era.

Vedāṅga literature

​​With the passage of time, the great spiritual efflorescence that gave the Ṛgveda seems to have waned. The next phase of Indian history was perhaps, inevitably, less inspired, less profound. The deeper significances of the mantras appear to get clouded; the language too was undergoing modifications. By the end of the Brāhmaṇa phase of the Vedic age, the spoken language had drifted far away from the language of the Sa\dot{m}hitā mantras.

There then arose the necessity of a conscious and meticulous preservation of the meaning as well as the external form of the mantras. One consequence of this was the emergence of concise texts called the Vedā\dot{n}gas (literally, limbs of the Vedas) recording certain specialised technical knowledge of the Vedic era. There are six Vedā\dot{n}gas: śikṣā (phonetics), kalpa (rituals), vyākaraṇa (grammar), nirukta (etymology), chandas (prosody) and jyotiṣa (astronomy). These subjects were systematised as auxiliary sciences essential to the proper understanding and cultivation of the Vedic texts. In these treatises, the important technical principles were codified in the form of aphorisms (extremely condensed statements) called Sūtras. We shall make a few remarks on this culture of brevity in Indian texts towards the end of this instalment.

The Vedā\dot{n}ga era marks a phase of transition between the numinous Vedic Age and the intellectual Classical Age of post-Vedic India. This transitional period witnessed, apart from the six Vedā\dot{n}gas, numerous other treatises which sought to systematise different branches of specialised knowledge into Śāstras, the presentations usually made in a Sūtra form. This transitional period is, therefore, referred to variously as the Age of the Śāstras or the Sūtra period.

Mathematical evidence in Vedāṅga and other Sūtra texts

Mathematical principles occur prominently in the portions of the Kalpa-Sūtras (the Vedā\dot{n}ga pertaining to rituals) known as the Śulba-Sūtras, and in the prosody text Chandaḥ-Sūtra of Pi\dot{n}galācārya.

The Kalpa-Sūtras include the Gṛhya-Sūtras (on household rituals like birth, marriage, etc.) and the Śrauta-Sūtras (on sacrificial rituals). The Vedic sacrificial rituals are of two types: the mandatory nitya (daily, perpetual) and the optional kāmya (desirable, for wish-fulfilment). The Śulba-Sūtras form a part of the Śrauta-Sūtras. The intricately designed fire-altars like śyenacit, k̄urmacit and rathacakracit are required for the more elaborate and expensive public kāmya rituals.

Baudhāyana, Mānava, Āpastamba and Kātyāyana are the respective authors of four of the most mathematically significant extant Śulba texts, the Baudhāyana Śulba-Sūtra being the most ancient. The existing Śulba-Sūtras do not lend themselves to precise dating and most historians of mathematics assign for Baudhāyana a date within 800–500 BCE. The archaic style of Baudhāyana is suggestive of an early date like 800 BCE.

The Śulba texts are the outcome of a long and sophisticated tradition of geometry and brick technology. It has been surmised that the Śulba geometry and brick technology have links with the Harappan civilization (cf. [20], p. 16; also see [3], pp. 241–242 and [32], pp. 119–121). In [28], the eminent mathematician and historian of mathematics A. Seidenberg had argued that the mathematical tradition behind the Śulba-Sūtras goes back to the second or third millennium BCE. The hypothesis of a Harappan link with Śulba-Sūtras resonates with Seidenberg’s conclusions. However, although the much-admired town-planning and architectural proficiencies of the Harappan or Indus valley civilization indicate a familiarity with basic computational and geometric techniques, at present we are not in a position to determine how much mathematics the Harappans actually knew. But, as emphasised earlier, the major mathematical results of the Śulba-Sūtras were known and applied in an earlier phase of the Vedic civilization. They are indispensable for accurate constructions of the intricate kāmya agni which occur in the Śatapatha Brāhmaṇa and the still earlier Taittirīya Sa\dot{m}hitā of the Yajurveda (which, according to some scholars, dates to 3000 BCE). We shall mention some of the mathematical gems from the Śulba-Sūtras in the next section.

Ancient Indians had the perception that the metrical form has greater durability, power, intensity and force than the unmetrical, and invariably recorded most of their important knowledge in verse form. The Vedic thinkers attributed a great esoteric significance to chandas. Special attention, therefore, was paid to the study of metres.

The oldest extant comprehensive treatise specifically on the science of metres is the prosody text Chandaḥ-Sūtra of Pi\dot{n}galācārya. This treatise contains interesting enumerative methods, including rules which are equivalent to the rules for converting the binary representation of a number into a decimal representation and vice versa. We shall give examples of mathematical ideas from Chandaḥ-Sūtra in a subsequent instalment.

Significant examples of mathematical knowledge are scattered in Jaina philosophical treatises. In the BhagavatīSūtra, there is a recognition that there are infinities of different “cardinalities” (sizes).

Emphasis on Importance of Mathematics in Vedic and Sūtra literature

Knowledge in Vedic India has been classified into aparāvidyā (textual knowledge) and parāvidyā (transcendental knowledge). Contrary to a common misconception, even the sacred Vedas too form a part of the aparāvidyā. The textual knowledge of the aparāvidyā was considered a helpful adjunct to the parāvidyā, but it has always been emphasised that the latter cannot be attained by the mere study of any text.

That the study of mathematics was given an elevated status in Vedic India can be seen from the fact that it is listed, along with the four Vedas, among the major branches of the aparāvidyā (Mundaka Upaniṣad 1.1.3-5).² In an episode narrated in the Chāndogya Upaniṣad (7.1.2.4), the sage Sanatkumāra asks Nārada, a seeker of the supreme Brahmavidyā, to state the disciplines of knowledge he had already studied. In his list, Nārada explicitly mentions mathematics and astronomy along with the four Vedas, the epics and certain other subjects.

The importance of mathematics is again emphasised in the Vedā\dot{n}ga literature. The Vedā\dot{n}ga Jyotiṣa (Yajurvedic recension 4) asserts:

The Jaina and Buddhist traditions too had a high esteem for the culture of mathematics. One of the four branches of Jaina religious literature is gaṇitānuyoga (exposition of the principles of mathematics). A mastery over sa\dot{m}khyāna (arithmetic) and jyotiṣa (astronomy) is stated to be one of the principal attainments of a Jaina priest. In Buddhist literature, the science of numbers and calculations (sa\dot{m}khyāna, gaṇana), is ranked among the noblest of the arts.

The Sthānā\dot{n}ga-Sūtra considers mathematics to be s̄ukṣma (subtle). The Sūtrākṛtā\dot{n}ga-Sūtra regards geometry as the “lotus of mathematics”.

Śulba Geometry: Illustrative Examples

Baudhāyana-Pythagoras Theorem

Central to many Śulba constructions is Baudhāyana’s version of the celebrated “Pythagoras Theorem”, a result of unknown antiquity named after the early Greek mathematician Pythagoras (c. 540 BCE). The familiar version of the “Pythagoras Theorem”, recorded by Euclid in his Elements (c. 300 BCE), states that the square of the hypotenuse AC of a right-angled triangle ABC equals the sum of the squares of the other two sides AB and AC. This result is a cornerstone of plane Euclidean geometry with applications throughout history. Baudhāyana Śulba-Sūtra (1.48) states the following equivalent version:

Literally,

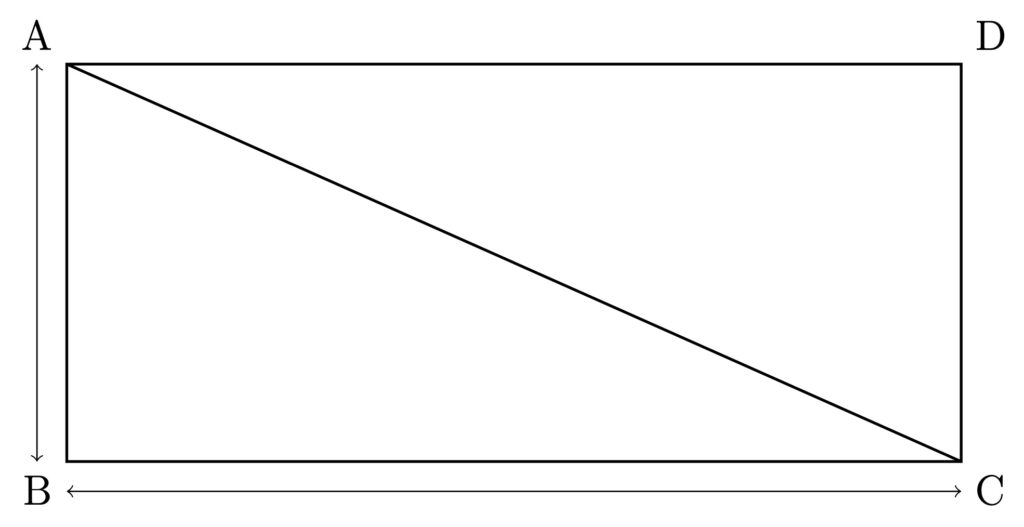With reference to the above diagram, Baudhāyana’s Sūtra states that the square on the diagonal AC of the rectangle ABCD is equal in area to the sum of the squares on the two adjacent sides AB and BC. Baudhāyana’s Sūtra (1.48) is probably the earliest extant explicit statement of “Pythagoras Theorem”. For convenience, we shall henceforth refer to Baudhāyana’s statement as “Baudhāyana-Pythagoras Theorem”. We again remind the reader that the result was known and applied in India and elsewhere, much before the time of both Baudhāyana and Pythagoras. As analyzed by B. Datta [4] and A. Seidenberg [28], the theorem was known at the time of the Vedic treatises Śatapatha Brāhmaṇa and the still earlier Taittirīya Sa\dot{m}hitā.

Āpastamba (1.4) and Kātyāyana (2.11) state the theorem in almost identical language as their predecessor Baudhāyana (cf. [4], p. 104); in the Kātyāyana Śulba, there is an additional phrase iti kṣetrajñānam indicating the fundamental importance of the theorem in geometry. Indeed, the theorem would play a pivotal role in much of ancient Indian geometry and trigonometry.

Before stating the quoted version, Baudhāyana (1.45) states the special case:

As the doubling of a square is necessary for the construction of certain altars mentioned in the Ṛgveda (oldest Veda), B. Datta concludes [[4], [p. 120]] that at least the above special case was known by the time of the Ṛgveda.

“Exact” Geometric Constructions and Geometric Algebra

To appreciate the depth of Śulba mathematics, consider the “straightedge-and-compass” constructions that make our present high-school Euclidean geometry appear so formidable to a large section of students. These constructions are to be performed using only a compass (for drawing arcs) and a straight-edge ruler (for drawing straight lines); the ruler (or the protractor) is not to be used for measurements of lines (or angles) during the constructions. For instance, if one is to bisect a given line, one is not allowed to simply measure the length with a marked ruler, and mark half of that length using that ruler; likewise, one cannot use a protractor to bisect a given angle. Note that measurements intrinsically involve an inaccuracy (because of which one has to take several measurements during scientific experiments) and hence have no place in the “straightedge-and-compass” constructions which are intended to be “exact” geometric constructions.

Apart from the problem of inaccuracy in measurement, there is a more serious theoretical problem: not all real numbers can be expressed as ratios of integers and hence not all lengths can be represented in a standard ruler. For instance, \sqrt{2} is not a rational number. Now if one is given a unit length and has to draw a square of 2 square units, one needs to draw a length of \sqrt{2} units. An accurate way of doing that will be to perform the standard “straightedge-and-compass” construction of a square on the unit length; the diagonal of the unit square will be exactly \sqrt{2} units. Such a construction is free from any measurement or approximation; hence is considered an “exact” construction.

A striking feature of the Śulba-Sūtras is the abundance of such “exact” geometric constructions of the “straightedge-and-compass” type. The instruments used in the Śulba constructions are rajju (ropes or cords), which play the role of both a (unmarked) straightedge ruler and a compass, and śa\dot{n}ku (poles or pegs) for marking positions; sometimes bamboo rods are mentioned in place of ropes.

The Śulba constructions often involve implicit use of algebraic formulae; in fact, the constructions yield geometric representations of the algebraic formulae. The expression “Geometric Algebra” is sometimes used in the history of mathematics to refer to such algebraic results in geometric form (cf. [28]).

Note that although the word “Algebra” is usually associated with the study of mathematical symbols, the symbols constitute only the external form of the subject. Although an important aspect of the subject, the use of symbols is not its only aspect, or even its main aspect. The heart of classical Algebra lies in the discovery and study of identities and equations, and these algebraic formulae have an existence irrespective of whether they are expressed through symbols, words, or any other means like geometric representations. For a modern expositor of ancient mathematical texts, it is imperative to recognize and highlight the presence of algebraic results in works like the Śulba-Sūtras, even when the algebraic ideas are not expressed formally through algebraic symbols. We shall come back to this point again at the end of this subsection.

We shall now present two examples of exact constructions from the Śulba texts, one combines a few squares to form a bigger square and the other converts a rectangle into a square. Both involve a subtle blend of geometric and algebraic thinking. Another exact construction will be described in a later section.

Construction of \sqrt{n}a from a

The Kātyāyana Śulba-Sūtra (6.7) describes the following construction of a square equal in area to the sum of the areas of n squares of the same size:

For clarity, we use a diagram (notation from the diagram will be added in square brackets in the translation below). We consider the side of each given square to be of length a units. Thus, the square to be constructed will have area na^2, i.e., each side of the desired square will be of length \sqrt{n}a.

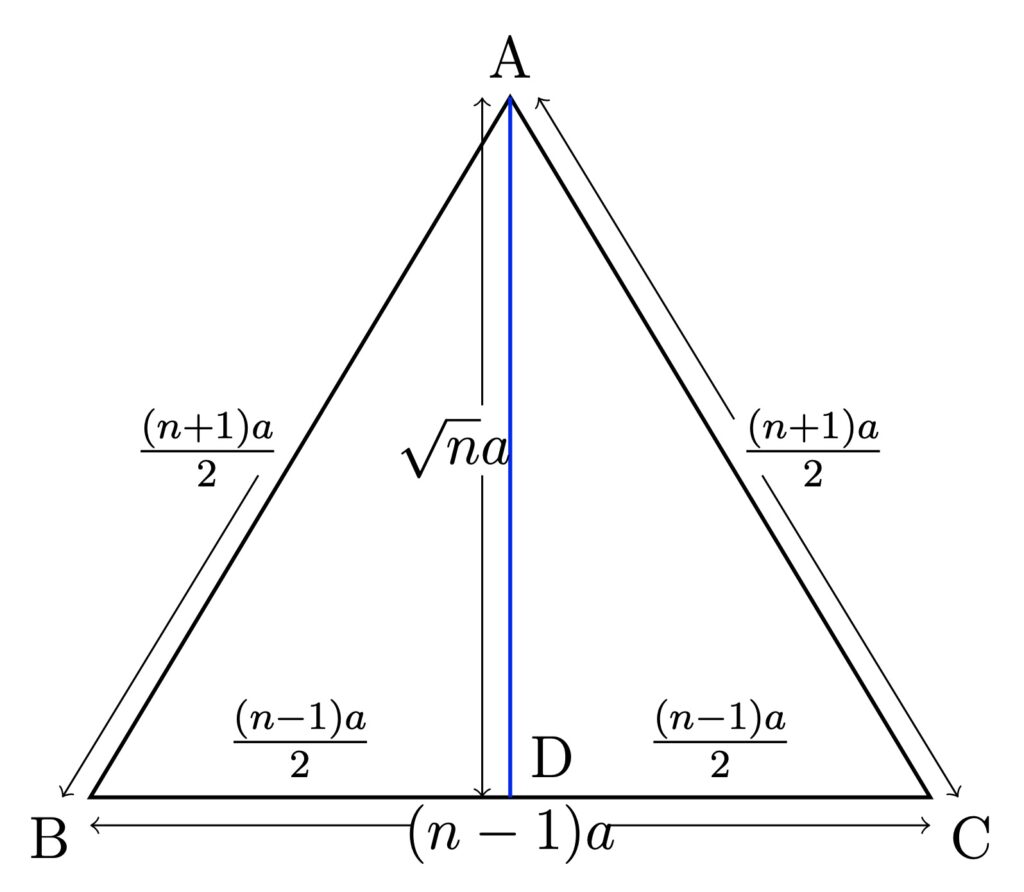
Here, BD = \frac{BC}{2}=\frac{(n-1)a}{2} and BA =\frac{(n+1)a}{2}, so that
\mathrm{DA}^2=(\frac{(n+1)a}{2})^2-(\frac{(n-1)a}{2})^2=na^2.

We emphasise five significant aspects of the above procedure. First, it gives an exact construction of \sqrt{n}a; no measurement or approximation is involved. Note that drawing a line of length \sqrt{n}a directly through measurement will necessarily be an approximation if n is not a perfect square.

Second, the construction makes an ingenious application of the Baudhāyana-Pythagoras Theorem and is one among the many examples in the Śulba-Sūtras which show that the Vedic savants knew why the theorem holds—a point which will be discussed later in this article.

Third, the construction involves an implicit use of the (unstated) formula
na^2=(\frac{n+1}{2})^2a^2-(\frac{n-1}{2})^2a^2;in fact, the construction is verily a geometric expression of the above formula from algebra.

Fourth, in the description of the procedure, the number of squares to be combined (which, for convenience, we denote by n) is arbitrary (not a fixed illustrative number), again reflecting an underlying algebraic mindset.

Fifth, it is a sophisticated example of combining a given set of mathematical objects (in this case, squares) to obtain a new object (here, a bigger square). On a related note, some of the greatest mathematical feats in ancient India involve the idea of “composition” or “combination” of mathematical objects, a fundamental concept in modern mathematics.

Construction of \sqrt{ab} from a and b

We now mention the Śulba procedure to construct a square equal in area to a given rectangle. Baudhāyana Śulba (1.54) states:

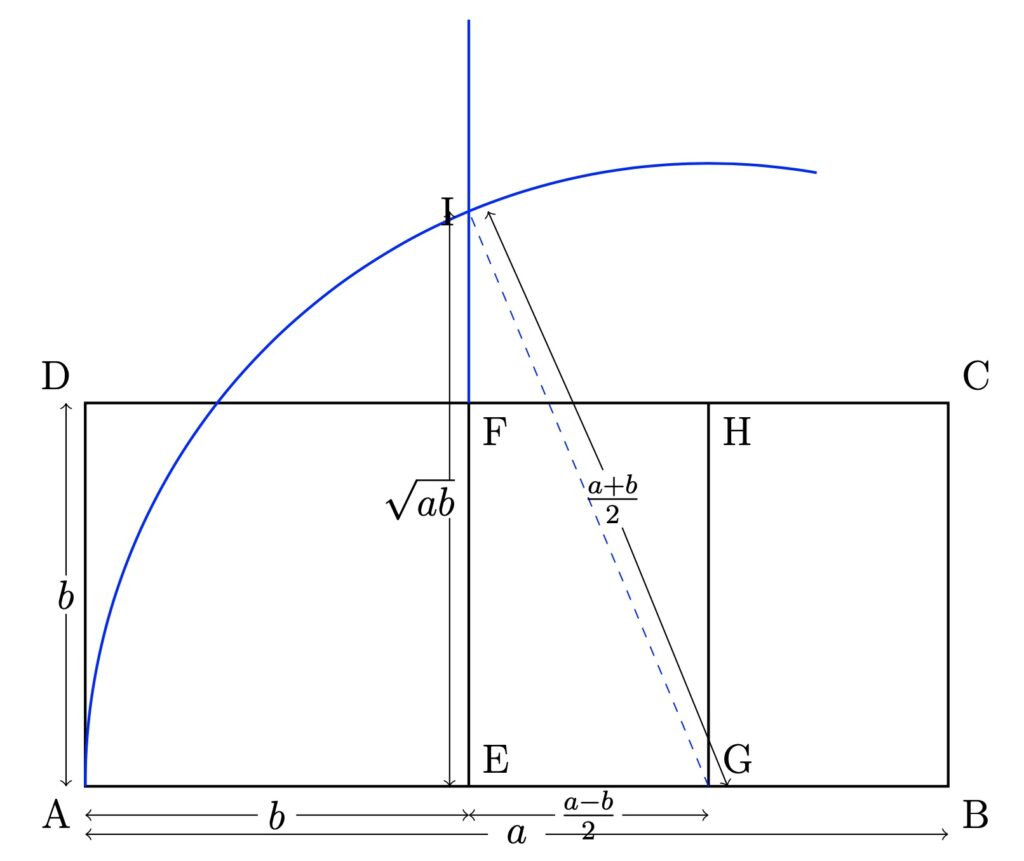For convenience, we make use of the diagram illustrating the verse. ABCD is the given rectangle of length a units and breadth b units.

Note that \mathrm{GE}=\frac{a-b}{2} and \mathrm{GI}=\mathrm {GA}=\mathrm{EA}+\mathrm{GE}=b+\frac{a-b}{2}=\frac{a+b}{2}, so that \mathrm{EI}^2=(\frac{a+b}{2})^2-(\frac{a-b}{2})^2=ab.

Again, note that the procedure makes an exact construction of \sqrt{ab} from a and b—there is no measurement or approximation. (Note that even when a and b are integers, drawing a line of length \sqrt{ab} through measurement will be necessarily approximate when the product ab is not a perfect square, which would often be the case.)

Not only does the construction involve a deep understanding of why the Baudhāyana-Pythagoras Theorem holds, it implicitly uses, and essentially provides a geometric formulation of, the algebra identity
ab=(\frac{a+b}{2})^2-(\frac{a-b}{2})^2.

The sophistication in the two representative Śulba constructions is there for everyone to see. Seidenberg [28, p. 318] remarks that the Śulba transformation of the rectangle into a square are:

Formation of a large square from a small square by adding gnomons

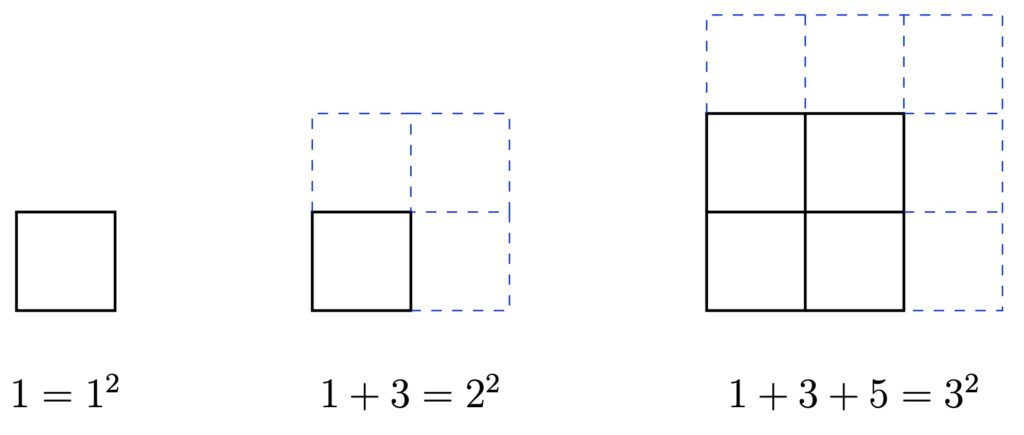We now mention another interesting idea of Baudhāyana, of a geometrico-algebraic flavour. Recall that a gnomon refers to the L-shaped figure that one gets when a (smaller) square is removed from a corner of a square. Baudhāyana describes how to form progressively larger squares, from a smaller square, by adding successive gnomons [4, p. 218].

This amounts to a geometric presentation, in fact, a geometric proof, of the algebraic identity
1+3+5+\cdots+(2n-1)=n^2.The algebraic identity would later be explicitly mentioned by Śrīdhara (750 CE) and other post-Vedic mathematicians as a method for determining the square of a number.

As per our present knowledge of the history of mathematics in India, the formalisation of algebra was to occur more than a millennium later, possibly around the time of Brahmagupta (628 CE). What is remarkable is that the Vedic savants did mathematics which was algebraic in spirit and substance (though not in form) several centuries before the genesis of formal algebra. This makes them even greater as algebraists. Indeed, it resonates with a similar sentiment on which the greatness of Gauss rests, that, even before the conscious emergence of the concept of “Groups” as an abstract mathematical structure, he did constructions amounting to imparting a group structure on an “equivalence class” of polynomial expressions called “binary quadratic forms”. (See also the Bhāvanā article [14, pp 16-17]).

Geometry of Circles and Approximations

When “exact” constructions of the “straightedge-and-compass” type are mathematically impossible, the Śulba authors describe convenient approximate constructions. To get a circle of area (approximately) equal to a square of side a units and diagonal d (=\sqrt{2}a) units, the Śulba authors Baudhāyana (1.58), Āpastamba (3.2) and Kātyāyana (3.13) prescribe drawing a circle of radius r=a+ \frac{d-a}{3} units, i.e., to take r= \frac{a}{3}(2+\sqrt{2}); for \sqrt{2}, they describe a numerical rational approximation equal to the fraction \frac{577}{408}. With this value, the area of the circle would be 1.017… a^2 square units, slightly more than a^2, the area of the given square. Mānava describes a more complicated formula for circling the square which yields a better approximation 0.995… a^2 square units (see [2] for details). The Śulba authors also give approximate formulae for the inverse problem of constructing a square with area that of a given circle. Modern algebra has confirmed that it is not possible to make “straightedge-and-compass” type constructions for the above two problems: circling a square and squaring a circle.³

The rational approximation to \sqrt{2}, expressed in the Śulba-Sūtras of Baudhāyana (1.61-1.62), Āpastamba (1.6) and Kātyāyana (2.13) in the form:
\sqrt{2} \approx 1+\frac{1}{3}+\frac{1}{3 \times 4}-\frac{1}{3 \times 4 \times 34} (=\frac{577}{408}),is significant both mathematically and historically. For readers familiar with “Simple Continued Fractions” (SCF), the fraction on the right-hand side is a convergent (the 8th convergent) of the SCF expansion of \sqrt{2} and hence it is the best possible approximation among all fractions with denominator \le 408 (cf. [12], p. 186). In terms of decimal fractions, \frac{577}{408} (=1.4142156…) matches \sqrt{2} (=1.414213…) up to five decimal places. The pair (577,408) satisfies the equation x^2-2y^2=1, a special case of an important equation investigated by Brahmagupta (628 CE) and other algebraists of the post-Vedic period. It is also involved in Ramanujan’s prompt solution of a mathematical puzzle which had surprised P.C. Mahalanobis that was discussed in the inaugural issue of this magazine (see [14], Box 2, p. 13). Simpler fractions \frac{7}{5} and \frac{17}{12} have also been used by Śulba authors as approximations for \sqrt{2}; they too have the property of being the most accurate among all fractions with denominators bounded by 5 and 12 respectively.

The pioneering work on the circle in the Vedic era appears to have had a significant impact on post-Vedic mathematicians and astronomers. The roots of post-Vedic Indian trigonometry, with its emphasis on the sine function, can also be traced to certain features of Śulba geometry: the fixing of cardinal directions (East-West and North-South lines), its geometry of circles and, of course, the Baudhāyana-Pythagoras Theorem (see [9] and [10]). One is also reminded of Brahmagupta’s brilliant results on quadrilaterals inscribed inside a circle. The Śulba approximations to \sqrt{2} have follow-ups in post-Vedic Indian mathematics which provides several methods for finding convenient, remarkably accurate rational approximations to numbers \sqrt{N} when N is not a perfect square (see [11], Section 7 (ii) for a few examples).

In the next article of the series, we shall see examples from the Śulba texts of the remarkable skill in computational arithmetic attained at such an early date.

Śulba Hints: Why Baudhāyana’s Theorem is True!

The Śulba-Sūtras are neither research monographs announcing new mathematical discoveries, nor expository mathematics textbooks in the sense of (say) Euclid’s Elements. They are essentially engineering manuals for the construction of fire-altars which include a concise compilation of requisite mathematical results and procedures which were already known over a long period of time. Formal mathematical proofs are outside the scope of these terse aphorismic texts. Thus, there are no specific Sūtras in the Śulba texts which explicitly announce any “proof” of the Baudhāyana-Pythagoras Theorem. However, the various Śulba constructions clearly show that the Śulba authors knew proofs of the Baudhāyana-Pythagoras Theorem in some form. As the 2014 Fields Medalist Manjul Bhargava aptly phrased it in a personal correspondence with the author: several Sūtras in the Śulba texts make it pretty clear that the Śulba authors “knew why the theorem is true”.

The reader can see for himself that the invention of the two Śulba constructions quoted in an earlier section would not have been possible without a discerning understanding of why the Baudhāyana-Pythagoras holds. We quote another Sūtra from Baudhāyana Śulba (1.50) which prescribes how to form a square equal in area to the sum of two given squares. It is stated shortly after the statement of the Baudhāyana-Pythagoras Theorem (1.48).

For convenience, we supplement the literal translation with a diagram:

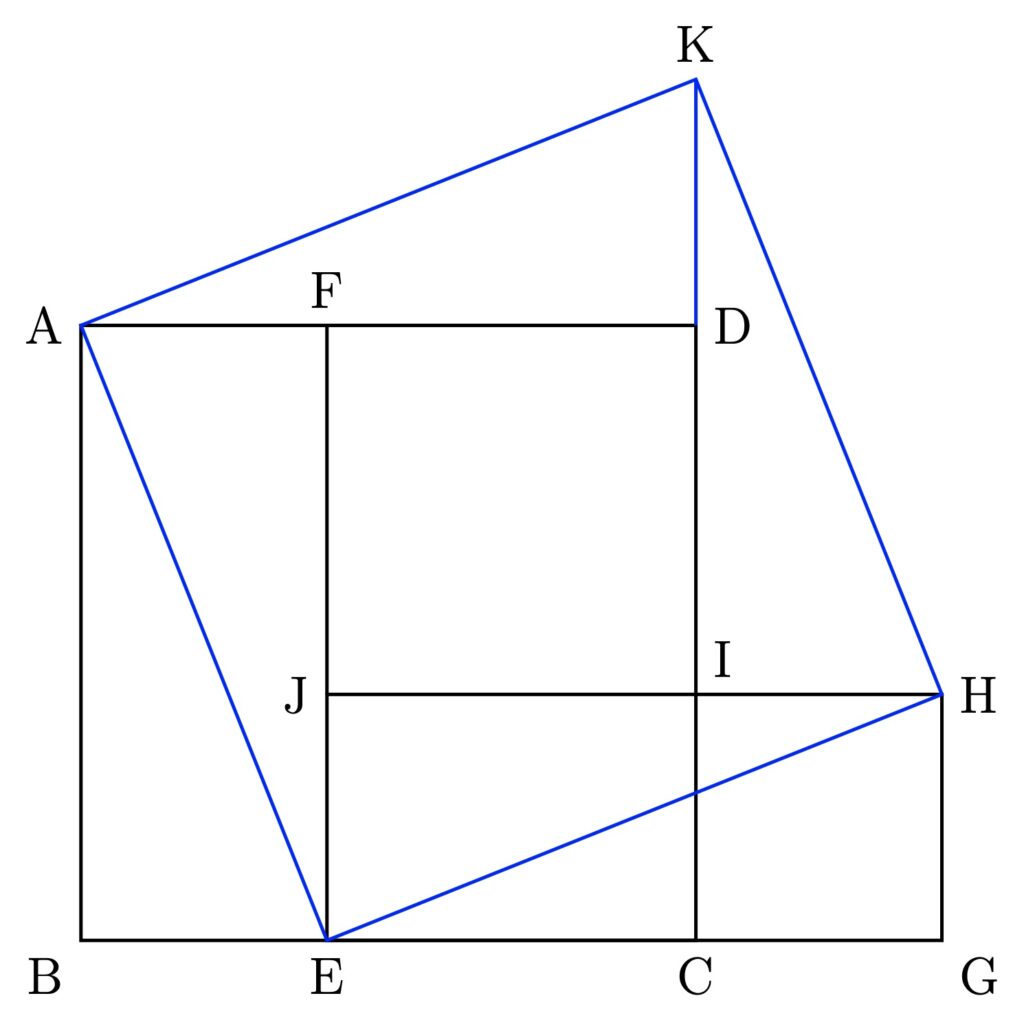
That the area of AEHK is the sum of the areas of ABCD and ICGH becomes obvious from the described diagram, observing that the triangles ABE and EGH are being replaced, respectively, by the congruent triangles KHI and ADK.

Now, this diagram is really a demonstration of the Baudhāyana-Pythagoras Theorem! For, it shows that the square AEHK on the diagonal AE of the rectangle ABEF is the sum of the square ABCD on the side AB and the square ICGH on the side CG(=BE). And it is interesting to note that in Baudhāyana’s treatise, this demonstration (1.50) comes almost immediately after the statement of the theorem (1.48); the intermediary Sūtra (1.49) gives numerical examples.

We mention here that pioneering Śulba scholars like G.F.W. Thibaut, Albert B̈urk, Hermann Hankel, Arthur Schopenhauer and B. Datta had maintained that the Śulba authors knew why the Baudhāyana-Pythagoras Theorem holds (see [4], Chapter IX, for details).

The terms Śulba and Geometry

Kātyāyana Śulba begins with the Sūtra

Literally,

The announcement shows that the main thrust of Vedic geometry lies in its constructions: the combinations (or transformations) of figures that can be done with rajju (ropes or cords). The word śulba is a Sanskrit synonym for rajju (rope or cord). Thus, the proper noun Śulba, as the name of a subject, could be interpreted as “Constructional Geometry”.

It is interesting to note that both the terms “Śulba” and “geometry” appear to have a common etymological genesis. The word “geometry” comes from the Greek words “geo” (earth) and “metry” (measuring). Seidenberg points out [27, [p. 520]] that the Sanskrit word “vedi”, or its root, means “earth” and draws attention to a passage in Śatapatha Brāhmaṇa (1.2.5.7) which says that since one obtains the entire earth by yajña (in a symbolic sense), the place of yajña is called vedi:

Seidenberg then suggests ([27], p. 520):

We mention here that, according to Seidenberg, sophisticated geometry originated in a very ancient ritual culture of a remote antiquity whose mathematical and ritualistic features can be seen in the Vedic civilization. To quote one of his statements [28, [p. 329]]:

Now, as B. Datta has pointed out [4, [p. 8]], the word śulba is derived from the root śulb meaning “to measure” and the terms śulba and rajju came to acquire several etymological significances: (i) the act or process of measuring, (ii) the entity measured (a line or a surface), (iii) the instrument of measuring (a rope or a cord) and (iv) the science of measuring (mensuration or geometry).

Paradoxically, measurement would no longer be a major theme in either the Śulba-Sūtras or Euclid’s Elements. The dominant motif in the Śulba treatises is “to construct” (with ropes or cords) rather than “to measure”. In fact, measurements are avoided in the “Geometry” of Euclid and in most of the Śulba constructions.

A keyword in Kātyāyana’s first Sūtra (quoted above) which encapsulates the spirit of Śulba mathematics is samāsa,
a Sanskrit word for “combination”, “composition”, “addition”, “union”. We have seen two examples: Baudhāyana Śulba (1.50) combining two squares of unequal areas and Kātyāyana Śulba (6.7) combining n squares of equal areas. Some of the most noteworthy contributions in ancient Indian mathematics involve the introduction or discovery of seminal principles of composition; the word bhāvanā was used in post-Vedic India for such composition laws. The most celebrated example is Brahmagupta’s bhāvanā (or samāsabhāvanā), an additive principle of composition of far-reaching importance (see [11], the Bhāvanā article [14] which has inspired the name of this mathematics magazine (Bhāvanā). The culture of combination was conducive for the early emergence of concepts like the weighted arithmetic mean as a representative value (see the Bhāvanā article [15]. Baudhāyana Śulba (1.50) may be regarded as a pioneering example of samāsa or bhāvanā in ancient Indian mathematics.

Śulba-Sūtras and Elements

The Śulba-Sūtras and Euclid’s Elements are two important extant source materials for ancient mathematics, and comparisons are perhaps inevitable. But certain differences in the characters of the two treatises are to be noted at the outset. First, the book Elements is meant to be a deductive treatment of mathematics—to use popular terminology, it is a text on “pure mathematics”. The Śulba-Sūtras are meant to be handbooks of known results in mathematics that are to be used in certain intricate engineering constructions—it is an instructional manual, a tract on applied mathematics. Therefore, one cannot expect in the Śulba-Sūtras all the features of a comprehensive textbook on pure mathematics, and one should not label the absence of such features as limitations or defects.

Second, the Śulba-Sūtras are offshoots of a much older Vedic tradition which had savants who had not only realized some of the fundamental principles of plane geometry, but knew why they worked and how they yielded accurate constructions. In this context, it may be pointed out that in the work of the original creators of any branch of mathematics, one usually finds only the working out of the essence of the discipline, and the essential insights (as distinct from empirical observations); a neat logical edifice of the subject emerges much later. The treatise of Pāṇini on Sanskrit grammar is an admirable instance of a logical edifice of a subject, but it was composed only after many centuries of creativity in the Sanskrit language, including expressions of some of the highest words of wisdom.

A relatively recent example from mathematics will further illustrate the point being made. H. Poincaré (1854-1912) is universally acknowledged as a founder of the branch of modern mathematics called “algebraic topology”, which emerged during the late nineteenth century; for, he had a deep insight into the essential ideas and results of the subject. However, an Elements-like axiomatic deductive treatment of the subject could emerge only after a subsequent effort of almost 50 years, culminating in the foundational work of Samuel Eilenberg, Norman Steenrod and others, during the 1940s. Poincaré is revered for his vision, and not frowned at for the absence of Eilenberg-Steenrod type axioms in his pioneering work. Similar is the history of algebraic geometry where the deep results of the Italian geometers of the nineteenth century could be put under a rigorous axiomatic framework only towards the middle of the twentieth century.

In the development of geometry, the Śulba-Sūtras give a glimpse of the H. Poincaré-type phase of the subject, while Elements corresponds to the Eilenberg-Steenrod phase. One cannot expect the Śulba manuals to present the subject as a logical structure built out of a set of postulates or axioms, in the manner of Elements, which itself is a culmination of developments over a few centuries.

The following remarks by J. Dieudonné [8, [p. 17]], about the work of Poincaré in topology may help us appreciate the nature of contributions of the pioneers of a subject, and guide us regarding what to expect (and what not to expect) from the work of the original creators of a discipline (italics in the quotations are ours):

Third, the Śulba treatises are composed as Sūtras (aphorisms), i.e., they are meant to indicate broad hints and not complete details. In fact, as in other disciplines, brevity is a general feature of ancient Indian mathematical treatises. There used to be an emphasis on the use of a learner’s own intellect for filling up the details. The culture of textual brevity might have contributed to the sustained creativity displayed by ancient Indians for several centuries. The terseness also fits with the Indian spiritual tradition. The secret meaning of the Vedic hymns was meant only for the spiritual seekers who would, after a certain stage of their development, find in the apparently enigmatic verses, the confirmations of their independent spiritual realisations.

Besides, there must have been a practical compulsion for conciseness of major texts. Palm-leaf manuscripts that were used in India do not last long. Thus a treatise could be preserved only through memorisation or through repeated copying. In either case, the more concise the work, the better its chance of survival through faithful memorisation or copying. Detailed expositions were transmitted orally.

Pioneering researchers and expositors on Śulba Mathematics

There has been considerable research and exposition on mathematics, especially geometry, in the Śulba-Sūtras. Among the researchers on Vedic geometry, a special mention has to be made of G. Thibaut, B. Datta and A. Seidenberg, each of them being pioneers in certain directions.

During 1874–77, the Indologist George Frederick William Thibaut (1848–1914) published the Baudhāyana Śulba-Sūtra with an English translation, thus introducing the treatise to the English-reading community. Moreover, he wrote a detailed essay [33] on the Śulba-Sūtras of Baudhāyana, Āpastamba and Kātyāyana, which is probably the first critical paper on the subject in a European language. This was followed by the work of B̈urk [1] on the Śulba-Sūtra of Āpastamba. It has to be noted that the analyses of Thibaut in his remarkable essay are not always free from inaccuracies and defects, which is understandable given that it is an early work on the subject (in English). The article [21] makes a few critical discussions on certain aspects of Thibuat’s works.

The book of Bibhutibhusan Datta (1888–1958) titled “The Science of the Śulba” [4], published by Calcutta University in 1932, contains a wealth of information and original insights on Śulba mathematics and its genesis. A D.Sc. in Applied Mathematics, Datta possessed the rare combination of professional mathematical experience with a deep knowledge of the nuances of ancient Sanskrit, literature and culture. A review of the book by R.C. Archibald (Isis 22 (1), 272-277 (1934)) notes:

Datta remarks in his Preface that the book had to be completed hurriedly on the eve of his retirement and “could not be made as comprehensive and thorough as it should have been”. Though he labels it an “imperfect sketch”, the fact remains that B. Datta’s “The Science of the Śulba” is an indispensable beacon for anyone seriously interested in Śulba mathematics. With A.N. Singh, Datta also wrote a general account on ancient Indian geometry which was published posthumously [7], several decades after it was written.

Abraham Seidenberg (1916–1988), a distinguished mathematician and historian of mathematics, has made an incisive analysis of Śulba mathematics in [27], [28] and [29]. Seidenberg made fundamental contributions in commutative algebra and algebraic geometry and his papers on the history of mathematics contain the master-touches of a modern mathematician steeped in algebra and geometry. His writings are also noted for their marvellous clarity of expression. Seidenberg is probably the first to emphasize that Vedic and Babylonian geometry are far too different in character (thereby rejecting the possibility of the former being a derivative of the latter), and to highlight that Vedic geometry has a feature of Greek geometry that is absent in Babylonian geometry—the straightedge-and-compass type constructions discussed in an earlier section. He also mentions the computational methods. In Seidenberg’s words [29]:

As we conclude the first part of this presentation, we mention a few other important references. C.N. Srinivasiengar has lucidly presented, in only 14 pages of his short book [31], a fairly detailed account on the Śulba-Sūtras. It is probably the first major publication (1967) in India on the Śulba-Sūtras after B. Datta’s writings.

A systematic presentation of ancient Indian geometry, including Vedic geometry, occurs in the book of Sarasvati Amma [24] published in 1979. This widely acclaimed book, based on her Ph.D. thesis (1963-64), remains the standard source-book for ancient Indian geometry, just as the two volumes of Datta-Singh remain the standard source-books for ancient Indian arithmetic and algebra. Original texts of the Śulba-Sūtras with translations and commentaries are given in [22], [25], [26] and [30]. There are several significant papers which discuss specific features of Śulba mathematics, some of which are listed in the bibliography [19], [23], [2] and [9]. The recent book of P.P. Divakaran [10] shares new insights on the topic. \blacksquare

References

1. A.D. B̈urk, Das Āpastamba-Śulva-Sūtra, Zeitschrift der deutschen morgenländischen Gesellschaft LV, 543–591 (1901); LVI, 327–391 (1902).
2. S.G. Dani, Geometry in the ŚulvaSūtras, Studies in the History of Indian Mathematics (ed. C.S. Seshadri), Hindustan Book Agency, New Delhi (2010).
3. M. Danino, The Lost River: On the trail of the Sarasvatī, Penguin (2010).
4. B. Datta, The Science of the Śulba, Calcutta University (1932); Cosmo Pub. (1993).
5. B. Datta, Vedic Mathematics, The Cultural Heritage of India Vol VI (Science and Technology) (ed P. Ray and S.N. Sen), The Ramakrishna Mission Institute of Culture, Calcutta (1986). Originally appeared in 1936.
6. B. Datta and A.N. Singh, History of Hindu Mathematics Part I, Motilal Banarasidass (1935); reprinted by Asia Publishing House (1962) and Bharatiya Kala Prakashan (2004).
7. B. Datta and A.N. Singh (revised by K.S. Shukla), Hindu Geometry, Indian Journal of History of Science 15(2), 121–188 (1980).
8. J. Dieudonné, A History of Algebraic and Differential Topology 1900–1960, Birkhäuser (1989)
9. P.P. Divakaran, What is Indian about Indian Mathematics? Indian Journal of History of Science 51(1), 56–82 (2016).
10. P.P. Divakaran, The Mathematics of India: Concepts, Methods, Connections, Hindustan Book Agency, New Delhi (2017).
11. A.K. Dutta, Brahmagupta’s Bhāvanā: Some Reflections, Contributions to the History of Indian Mathematics (eds. G.G. Emch, R. Sridharan, M.D. Srinivas), Hindustan Book Agency, New Delhi (2005).
12. A.K. Dutta, Kuṭṭaka, Bhāvanā and Cakravāla, Studies in the History of Indian Mathematics (ed. C.S. Seshadri), Hindustan Book Agency, New Delhi (2010).
13. A.K. Dutta, Was there sophisticated mathematics during Vedic Age? Platinum Jubilee Memorial Volume, Ramakrishna Mission Vidyamandira, Belur Math, 361–385 (2016).
14. A.K. Dutta, The bhāvanā in Mathematics, Bhāvanā 1(1), 13–19 (2017).
15. A.K. Dutta, Weighted Arithmetic Mean in Ancient India, Bhāvanā 1(4), 24–36 (2017).
16. A.K. Dutta, Mathematical Gems in Vedic and Sūtra Literature, to appear in the Proceedings of the National Conference on “Indian History: Emerging Perspectives” (5–7 March 2018), edited by Nandita Krishna, Indian Council of Historical Research.
17. Algebraic Insights in Indic Algorithms, to appear in “The Computation Meme: Explorations in Indic Computational Thinking” edited by K. Gopinath and Shailaja D. Sharma, IISc Press.
18. R.N. Iyengar, Dhruva the Ancient Indian Pole Star: Fixity, Rotation and Movement, Indian Journal of History of Science, 46.1, 23–39 (2011)
19. D.W. Henderson, Square Roots in the Śulba Sūtras, Geometry at Work (ed C. Gorini), MAA, Washington DC, 39–45 (2000).
20. G.G. Joseph, Indian Mathematics, World Scientific (2016).
21. A. Keller, Overlooking mathematical justifications in the Sanskrit tradition: the nuanced case of G.F.W. Thibaut, The History of Mathematical Proofs in Ancient Traditions (ed. K. Chemla), Cambridge (2012).
22. S.D. Khadilkar (ed.), Kātyāyana Śulba Sūtra, Vaidika Samsodhana Mandala, Pune (1974).
23. J.F. Price, Applied Geometry of the Śulba Sūtras, Geometry at Work (ed C. Gorini), MAA, Washington DC, 46–55 (2000).
24. T.A. Sarasvati Amma, Geometry in Ancient and Medieval India, Motilal Banarasidass, Delhi (1979; 1999).
25. Satya Prakash and Sharma R.S. (eds.), Baudhāyana Śulba Sūtra, Research Institute of Ancient Scientific Studies, New Delhi (1968).
26. Satya Prakash and Sharma R.S. (eds.), Āpastamba Śulba Sūtra, Research Institute of Ancient Scientific Studies, New Delhi (1968).
27. A. Seidenberg, The Ritual Origin of Geometry, Archive for History of Exact Sciences 1, 488–527 (1962).
28. A. Seidenberg, The Origin of Mathematics, Archive for History of Exact Sciences 18, 301–342 (1978).
29. A. Seidenberg, The Geometry of Vedic Rituals, Agni, The Vedic Ritual of the Fire Altar Vol II (ed F. Staal), Asian Humanities Press, Berkeley, 95–126 (1983); reprinted Motilal Banarasidass.
30. S.N. Sen and A.K. Bag (eds.), The ŚulbaSūtras, Indian National Science Academy, New Delhi (1983).
31. C.N. Srinivasiengar, The History of Ancient Indian Mathematics, The World Press Private Ltd., Calcutta, 1967; reprint 1988.
32. F. Staal, Greek and Vedic Geometry, Journal of Indian Philosophy 27 (1/2), 105-127 (1999).
33. G. Thibaut, On the Śulva-Sūtras, Journal of the Asiatic Society of Bengal XLIV, 227–275 (1875).

Footnotes

1. The article titled The Bakhshali manuscript and the Indian zero by P.P. Divakaran discusses this point on pages 17 and 18 of the October 2018 issue of Bhāvanā. ↩
2. These references convey something like they are from Chapter 1, Section 1 verses 3–5, but what exactly it means in Sanskrit terminology will carry appropriately specific interpretations. ↩
3. The history of these problems in discussed in detail in Dave Richeson’s book reviewed in the July 2021 issue of Bhāvanā. ↩